International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2018) Volume 9, Issue 2
To design any manufacturing setup we need to focus on design of facility layout and it has a huge impact on the performance of the manufacturing system. so the Optimum arrangement of layout is important in order to achieve high productivity in flexible manufacturing system (FMS). The objective of the loop layout problem is the determination of the ordering of machines around a loop, to minimize the total number of loop traversals for a family of parts. The problem we address is to design the layout of the system so that the number of machines that the part types cross in their manufacturing process is minimized. We formulate the problem mathematically and solve it by a meta-heuristics that obtains consistently better results than an earlier popular method. Since, optimum arrangements of layout is a combinatorial problem so finding the best combination out of millions of combinations is a challenging task and can't be solve using conventional techniques. Therefore, this paper details the design, development and testing of particle swarm optimization (PSO) technique to solve the loop layout problem. The proposed method is validated with bench mark problems. Here PSO algorithm is proposed for obtaining the optimal solution of unidirectional loop layout design problem of various FMS models.
Keywords: Flexible manufacturing system; Loop layout; Particle swarm optimization; Loop layout design problem
Flexible manufacturing systems (FMS) play a crucial role in modern complex production lines. Such systems generally consist of a group of machines capable of performing a number of different operations, interconnected through an automated parts-transportation and handling mechanism all operating under the hierarchical control of a common computer system. An important factor in designing a FMS is the determination of an effective layout of the machines, i.e., an optimum arrangement of the machines in the shop floor so that to provide efficient operation. The layout of the machines has a significant impact to the material-handling cost, the time of processing, the throughput of the production system, and therefore affects the overall productivity of the FMS. The layout of machines in a FMS is typically determined by the type of material-handling device used such as material-handling robots, automated guided vehicles (AGVs), gantry robots, etc. In practice, the most commonly used types of machine layouts are the following (Figure 1): the linear single-row layout (Figure 1a), the linear double-row (Figure 1b), the cluster layout based on gantry robot (Figure 1c), the semi-circular layout with a single robot, (Figure 1d), and the closed-loop layout (Figure 1e). In the first two layouts (Figures 1a and 1b) an AGV transports parts between the machines moving in both directions in a straight line. The third machines layout (Figure 1c) based on a gantry robot is used when the space in the shop floor is limited. In the fourth layout (Figure 1d) a material-handling industrial robot carries parts between the machines traversing with its end-effector a semi-circular (pre-specified) trajectory. While, in the closed-loop layout, a conveyor moves in a closed-loop rail in only one direction transporting parts among the machines. This work addresses the unidirectional loop layout design problem (LLDP), i.e., the problem of designing loop-layout-manufacturing systems of the form shown in Figure 1e.
Afentakis [1] has developed an interchange heuristic to solve the loop layout problem and modelled the layout of an FMS by a graph, whose nodes represent process components and whose edges denotes the interconnection links of the material handling system. Kaku and Rachamadugu [2] have presented quadratic assignment problem (QAP) formulation approach to unravel loop and linear layout problems in FMS. Kouvelis and Kim [3] developed a heuristic and branch and bound (BB) procedure to unravel unidirectional loop network downside and conjointly planned a decomposition principle to deal giant work flow matrices. Leung [4] has developed a heuristic supported graph theory that constructs a layout from an answer to the linear programming relaxation of the matter.
They introduced integer programming (IP) formulation to unravel unidirectional loop layout downside that thought-about each the MIN_SUM and MIN_MAX objectives. Cheng et al. [5] have developed hybrid genetic algorithm and neighbourhood search to unravel the loop layout downside. Tansel and Bilen [6] have planned 2 heuristics known as MOVE and MOVE/INTERCHANGE to unravel the simplex loop network layout downside. The first heuristic was primarily based on positional moves and the second one was based on both positional moves and pair wise interchanges. Potts and Whitehead [7] have modelled a FMS loop layout problem that combines scheduling and machine layout problem and solved through a three-phase IP model. The first phase balances the machine workload by assigning operations to machines. The second phase minimizes inter-machine travel, and the third phase assigns the positions around a conveyor belt loop so that the total number of circuits is minimized. Both heuristic and BB algorithms were proposed by Lee et al. [8] to solve unidirectional loop layout problem. Bennell et al. [9] proposed an iterated decent and tabu search algorithm and a randomized insertion algorithm to solve min–max loop layout problem. Malakooti [10] presented a heuristic procedure for solving the unidirectional loop network based on linear programming formulation which utilizes the flow matrix to solve the problem. Altinel and Oncan [11] have discussed about the various formulations and proposed heuristics to solve unidirectional cyclic layout problem. Nearchou [12] has used a differential evolution algorithm (DEA) to solve the loop layout problem and proposed a mapping mechanism for encoding the floating point chromosomes for combinatorial problems with permutation property. The loop layout problem is NP hard type and non-traditional optimization techniques have been employed to solve these kinds of problems. In this paper an attempt has been made to implement PSO algorithm for designing loop layout manufacturing system. The MIN_SUM congestion measure is considered as an objective. The configuration of layout in which machines with unequal clearance between them is considered in order to reflect the real manufacturing facilities [13-18].
A common layout in FMS is the loop layout in which the machines are arranged in a loop network and materials are transported in unidirectional as shown in Figure 2. An important step in designing the unidirectional network is the determination of the ordering of the machines around the loop. A loop layout design can be represented as permutation of machines (m1, m2...mn) with a prefix of loading/ unloading station 0. Each part is characterized by its part route, the sequence of machines it must visit to complete its processing. For a given part, suppose processing on machine j immediately follows processing on machine i. If the position of machine j is lower than that of machine i, then the part must cross the loading / unloading station, which is called a reload. The number of reloads necessary to complete the processing for a part is defined as a measure of traffic congestion. The use of traffic congestion is a measure to evaluate the loop layout. The congestion is defined as the number of times a part traverses the loop before its processing is completed. The two kinds of congestion measures used in loop layout design are MIN_SUM and MIN_MAX. A MIN_SUM problem attempts to minimize the total congestion of all parts while a MIN_MAX problem attempts to minimize the maximum congestion among family of parts.
Problem formulation
The objectives of the problem are formulated as:
Minimization of average cost of best loop layouts
The objectives of the problem are formulated as:
1. Minimization of average cost of best loop layout
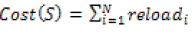
Where, S is the best loop layout combination
Reload is the crossing through loading/unloading station
N is number of parts
2. Minimization of average percentage solution effort (%SE) spent by algorithm
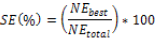
Where, NEbest is the number of evaluation to get the best result.
Netotal is the total number of evaluations
3. Minimization of congestion for each part
MPi= reloadi
Where, MPi is the ith part of machine MP.
PSO: an overview
PSO may be a stochastic optimization technique lies on population and represented on the social behaviours discovered in animals or insects, for example flocking of birds, schooling of fish, and animal herding. One vital tool of a successful swarm intelligence model is PSO that was invented by Russell Eberhart, an electrical engineer, and James Kennedy, a social psychologist, in 1995. Originally PSO won’t to solve non-linear continuous optimization issues; however, a lot of recently it’s been employed in several sensible, real-life application issues. PSO attracts inspiration from the social science behaviour related to flocking of birds. It’s a common observation that birds will fly in massive teams with no chance of collision for very long travel, creating use of their training to keep up an optimal distance between themselves and neighbours.
PSO algorithm
Particle swarm optimization follows some pre-specified steps to implement as shown in Figure 3.
Step 1. Initiate ‘n’ no of particles at random.
Step 2. Find fitness value of every particle. And apply the condition; if the fitness value is optimum than the best fitness value (pbest) in past. Set the present value as the next pbest.
Step 3. Select particles with the best fitness value of whole particles as the gbest.
Step 4. For every particle, calculate particle speed in line with the formula
Vk [t+1] =Vk [t] +C1 r1 (Pkbest –Pk) +C2 r2 (Gkbest – Pk)
Where, Vk [t] represents the particle speed.
Pk represents that the current particle.
Pkbest represents that the personal better of particle
Gkbest is that the global better of particle
r1 and r2 is a random number lies in the interval (0-1), Assume r1 =0.78 r2=0.48
C1, C2 are learning factors (or) social and cognitive parameters. Usually C1 = C2 = [0-4] Assume C1 = C2 =1.
Step 5. Velocities of particles on every dimension are added to a most speed Vmax, the rate on the factor is restricted to Vmax.
Step 6. Now terminate if an optimal value is reached. Otherwise, move to Step 2.
To apply any method for evaluating the system it is extremely necessary to repair some numerical coefficients for the response of parameters. PSO owing to the power of global optimization depends mostly on setting of those parameters. The optimal valves of parameter are fixed on trial and error basis which is listed below.
• Size of population =100,
• Velocity factors=C1=C2=2
• Termination criteria=300 iterations
For every test problem, the rule is applicable to run up to a most of 30000 number of evaluations. The analysis conforms to a single computation of target function for the candidate solution. To implement the PSO codes to the loop layout of the FMS system two models are taken with the following specifications as shown in Table 1. The data set details of required machine sequence for these models is also shown in Tables 2 and 3. Initially the PSO codes are verified on the standard optimization function such as Rosenbrock function and Ackley function.
| S.No. | Description | M-1 | M-2 |
|---|---|---|---|
| 1 | Number of machines | 10 | 15 |
| 2 | Number of parts | 3 | 9 |
| 3 | Layout considered | Loop layout | Loop layout |
Table 1: FMS model building (M-model).
| S.No | Total machines | Total parts | Part number | Required sequence of machine |
|---|---|---|---|---|
| 1 | 10 | 3 | 1 | 2-1-6-5-8-9-3-4 |
| 2 | 10 | 3 | 2 | 10-8-7-5-9-6-1 |
| 3 | 10 | 3 | 3 | 9-2-7-4 |
Table 2: Required sequence with batch sizes of 10 machines with 3 parts.
| S.No | Total machines | Total parts | Part number | Required sequence of machine |
|---|---|---|---|---|
| 1 | 15 | 9 | 1 | 4-2-5-1-6-8-14-9-11-3-15-12 |
| 2 | 15 | 9 | 2 | 3-2-15-14-11-1-7-10-4-5-13-6-9 |
| 3 | 15 | 9 | 3 | 5-6-11-15-2-12-3-4 |
| 4 | 15 | 9 | 4 | 10-9-4-14-2-3-15-8 |
| 5 | 15 | 9 | 5 | 11-2-4-14-5-3-15 |
| 6 | 15 | 9 | 6 | 8-10-12-11-15-13-1-14-4-5-3 |
| 7 | 15 | 9 | 7 | 5-11-10-3-7-13-8 |
| 8 | 15 | 9 | 8 | 7-3-2-8-4-10-6-15-13-9-1 |
| 9 | 15 | 9 | 9 | 11-13-3-1-12-14-4-8-9-2 |
Table 3: Required sequence with batch sizes of 15 machines with 9 parts.
Then the generation of global minima of functions provides the validation of the algorithm that is going to be used for the layout optimization of FMS.
The PSO Algorithm is tested over the randomly generated test problems. The model buildings of two different models are tabulated and the required machine sequence for the test problems are given in Table 3. The proposed algorithm is tested on FMS Model test problems:
For model 1 - 10 machines and 3 parts
The PSO codes are now applied to the FMS model-1 in which 10 machines and 3 parts are considered and parameters are calculated by the 100 evaluations. The following results are tabulated below in Table 4. The applied code is dynamic that is we can apply the number of evaluation and the model parameters to find the output of the objective functions. As the number of evaluations increases, accuracy of the result is also increases.
| S.No. | Calculated Parameters | Value |
|---|---|---|
| 1 | Minimum cost | 3Rs |
| 2 | Optimal sequence | 10-8-9-3-2-7-4-1-6-5 |
| 3 | Total evaluation | 100 |
| 4 | Congestion for each part | 1-2-0 |
| 5 | Solution Effort (%) | 1% |
Table 4: Output parameters of model-1.
Plots of objective function results for model-1:
Plot of no of iterations vs. cost: Figure 4 shows the output plot of the model-1 in which the plot is produce between number of iterations and the cost. From graph, we can see that there is a constant increment in cost for the increased no. of iterations corresponding to the 3Rs. So we can say that the optimum cost is 3Rs.
Plot of total evaluation vs. optimal cost: Figure 5 shows the output plot of the model-1 in which the plot is produce between number of evaluations and the best cost. And the best cost achieved in each evaluation is also plotted and mark by red star. From graph, we can see that there is a different best cost value for each evaluations and minimum cost achieved by the some evaluations are 3Rs, so this cost (3Rs) is the optimal cost for model-1.
For model 2 - 15 machines and 9 parts
The PSO codes are now applied to the FMS model-2 in which 15 machines and 9 parts are considered and parameters are calculated by the 100 evaluations. The following results are tabulated below in Table 5.
| S.No. | Calculated Parameters | Value |
|---|---|---|
| 1 | Minimum cost | 24 Rs |
| 2 | Optimal sequence | 7-4-5-11-10-3-15-13-2-1-6-8-12-14-9 |
| 3 | Total evaluation | 50 |
| 4 | Congestion for each part | 2-4-3-3-2-3-1-3-3 |
| 5 | Solution Effort (%) | 54% |
Table 5: Output parameters of model-1.
Plots of objective function results:
Plot of no of iterations vs. cost: Figure 6 shows the output plot of the model-2 in which the plot is produce between number of iterations and the cost. From graph, we can see that there is a constant increment in cost for the increased no. of iterations corresponding to the 24Rs. So we can say that the optimum cost is 24 Rs.
Plot of total evaluation vs. optimal cost: Figure 7 shows the output plot of the model-2 in which the plot is produce between number of evaluations and the best cost. And the best cost achieved in each evaluation is also plotted and mark by red star. From graph, we can see that there is a different best cost value for each evaluations and minimum cost achieved by the some evaluations are 24Rs, so this cost (24Rs) is the optimal cost for model-2.
In this paper, a PSO based approach is successfully applied on obtaining the optimal solution of unidirectional loop layout design problem. In this work the minimization of total traffic congestion, minimization of total cost in terms of reload and minimization of solution effort have been considered as an objective. The proposed algorithm is tested on different combinations of machines to validate the performance of algorithm, and the obtained results are very promising.
It is seen that the PSO algorithm is efficient in finding good quality solutions for the layout problems with less percentage solution effort. Random combination approach is used in this work to remove the problem of exploitation. In this paper tests have been performed for maximum of 300 evaluations while many researchers performed tests for 30000 or even more than 50000 evaluations. As the number of evaluations will be more, probability of getting optimum combination will be more.
As a future work the PSO algorithm can be extended to solve the loop layout problem based on MIN_MAX criteria and bi-directional loop layout problems.