International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2018) Volume 9, Issue 3
In this paper, based on PI design principles for multivariate systems, a control system is designed that can meet the control requirements such as tracking velocity and regulating stator current with considering effects of suspension system on propulsion system. The dynamical model of linear synchronous motor with DC excitation used in the EMS maglev trains for propulsion is presented. In this system, the magnetizing inductances in the direction of the d and q axes are dependent on suspension air gap. So, by changing the suspension air gap from its desired value due to disturbances, these parameters change and consequently affect the performance of the motor, and the motor will be deviated from work point and the train will not follow its desired speed. The control system designed can compensate effects suspension system on propulsion system. Finally, the simulations confirm the performance of this controller.
Keywords: Maglev transrapid train EMS; Sliding mode control; Linear synchronous moto
The maglev train is one of the fastest transportation vehicles which are appropriate solution to the problem of traffic and energy efficiency. With increasing population and the development of population centers, road and air transportation can no longer be a massive response. Accordingly, demand for innovative public transportation has increased. In order to provide a convenient public service, the new generation transport system must have special conditions such as speed, reliability and safety. In addition, the system should have features such as comfort, lower weight, low security availability and low maintenance costs. It should also not be contaminated with the environment and is suitable for mass transportation. Magnetic suspension trains or Maglev are one of the best options for meeting these needs. The suspension of the Maglev trains is accomplished by two types of suspension technology EMS and EDS. The methods are distinguished, respectively, by electromagnetic attraction forces and electromagnetic repulsive forces, respectively. EMS method or electromagnetic suspension, by creating attraction forces between electromagnets of suspension system and the surface under the steel rails, causes the train to be suspended at a distance of 1 cm from the surface under the rails. Also, by creating attraction forces between the rail lateral wall and electromagnets placed on the bogie lateral surface, they create an air gap of one centimeter from the lateral wall of the rails. The EDS method or the electrodynamic suspension is similar in many respects to the EMS method. But in this way, the electromagnets, by creating a repulsive force from the guide way, cause the train to be suspend. These electromagnets are superconducting and they can direct the electricity current shortly after the feeding is cut off. Maglev EMS trains is considered in this article. Due to unstable and nonlinear dynamics, the suspension of the Maglev EMS trains requires the stabilization and control of the air gap of suspension electromagnets. On the other hand, the placement of a train at a specified position is achieved when it can control the output speed. Detection of speed and position is done by speed and position sensors. The sensor output is compared with the reference profile, which is a trapezoidal profile. The deviation from the reference profile must be compensated by the controller. This compensation is done by applying the propulsion force generated by the LIM or LSM motor or by braking. By applying this force, the speed of the train is controlled, and thus the train is placed in a desired position. Due to the reasons mentioned above, in order to achieve the optimum air distance in the suspension system and also to control the train speed, optimal speed control systems are needed. For the reasons mentioned, in order to achieve the desired air gap in the suspension system and also to control the train speed, control systems are required that can meet the control requirements based on the dynamics of the suspension and propulsion systems. In the early year 1920, Hermann Kemper presented the concept of magnetic suspension trains which use magnetic attraction forces to create magnetic suspension. Kemper followed this concept from 1930 to 1940. And he was able to be created a practical plan for the Maglev train. He published this plan in an article in 1953. Transrapid International Company is one of the first designers and top manufactures of Maglev train. The first Maglev train was manufactured in 1971. The progress of the Maglev trains was carried out between 1971 and 2009. In 2008, the new TR09 operational tests were carried out at the Trans-Rapid Laboratory in the city of Emsland and were completed in 2009. German Alfred zeden presented the idea of using a linear motor in creating propulsion force and EMS train movement in an article entitled "Electric Traction Apparatus". The propulsion force of the Maglev trains generate by a linear motor. Linear motors are made by changing the physical structure of rotary motors. In rotary motors, the rotor and stator are cylindrical. If the stator and rotor of these motors are cut and opened, as shown in Figure 1, they become linear motors. Figure 1 shows the concept of a linear motor derived from a rotary motor. In order to control the propulsion system on the Maglev train EMS, a dynamic model of linear synchronous motors is required. According to Krause et al. [1], an equivalent electric circuit and therefore a mathematical model of a rotary synchronous motor are presented. A mathematical model of linear synchronous motor dynamics is presented [2]. This model is derived using the orthogonal model of rotary synchronous motors and with pertinent adaptations. The PSO-PID, TSPSO, and STSPSO TS control patterns have been used to control the propulsion and suspension of the Maglev transportation system [3], But to describe the dynamics of the Maglev transport system, a second-order differential equation has been used which the differential equation’ variable is a matrix with five freedom degrees of train. Since in the Maglev trains EMS the suspension actuator is suspension electromagnets and propulsion actuator is linear synchronous motors, Dynamic equations of this actuators are not considered. A PID control algorithm that is based on the PSO optimization is presented for controlling the suspension and propulsion of a Maglev transportation system [4]. The proposed PSO-PID control system has a better performance than SM control strategies, but motor dynamics model as an actuator is not considered. The design of a propulsion and suspension on line controller for a magnetic suspension transportation system is presented [5]. First, a general dynamic model of a Maglev transportation system is presented, and then a sliding mode control strategy (TS) is introduced. Disturbance is generally considered as a sinusoidal function. The design, modeling and control of multi polar linear synchronous motor are presented [6]. The Japanese Maglev system analysis is provided that uses only one set of coils for guidance, suspension and propulsion in guide way [7]. In practice, magnetic suspension trains EMS use electromagnets actuators to suspend the train. These actuators are, in fact, electromagnets with a core of iron that are embedded in the bogie of the train and create a suspension by creating a magnetic field due to the electric current of their windings. The suspension air gap is controlled by setting the current of the suspension electromagnets by the suspension controller.
The propulsion of the Maglev train EMS is performed by a DC excitation linear synchronous motor. In order to meet the control requirements of the Maglev train EMS propulsion system, especially the train speed control, in the design of the speed controller, the dynamical equations of the DC excitation linear synchronous motor as a propulsion system actuator should be considered. The suspension system or rotor of motor, in addition to the suspension, acts as an excitation system for the DC excitation linear synchronous motor. When the magnetic field caused by the suspension electromagnets (excitation system) is synchronized with the magnetic field caused by the three-phase stator coils, propulsion force is produced proportional to the speed of the train, causing the train to move on the rails. On the other hand, in the event of disturbance in the suspension system and as a result, the suspension air gap deviation from the desired value of one centimeter, motor inductances change and cause a parametric uncertainty in the motor model. So with the design of an appropriate controller, the disturbance effects of the suspension system must be minimized. In this article, first an electromagnetic, electrodynamic and dynamic model of Linear Synchronous Motor with DC excitation are presented and the next section, a dynamic model is presented to describe the function of linear synchronous motor. In order to investigate the effect of suspension air gap changes on the performance of the propulsion system, an analytical relation is extracted for magnetizing inductances in direction with d and q. Then, in order to achieve the control objectives of the propulsion system, using a controller design principles for a multivariate system, a PI linear controller is designed.
Electromagnetic, Electrodynamic and Dynamic model of Linear Synchronous Motor with DC excitation
DC excitation linear synchronous motor (DCE-LSM) with acactive and flat stator configuration (Figure 1) is used in high-speed trains EMS with active guide way [2].
The linear synchronous motor excitation in the trains EMS is DC excitation type. In this type of motor, the DC exciters also control the suspension of the train in addition to creating excitation. The propulsion force in this type of motors is caused by the interference of the magnetic field of DC exciters and the magnetic field of the three-phase ac stator. The propulsion force produced in this motor is proportional to the speed of the train. Therefore, in order to control the speed of the train, the propulsion force and, in fact, linear synchronous motor must be controlled. In this section, Electro-magnetic, electrodynamic and dynamic model for linear acoustic motors of DC excitation type are presented Using the electromagnetic model of the rotary synchronous motor, three-phase and salient pole in the coordinate dq.
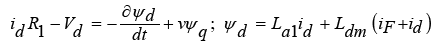
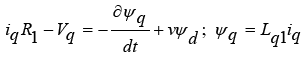
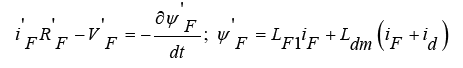
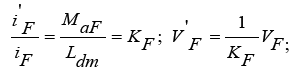
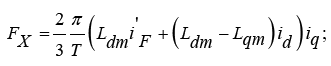
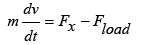 (1)
(1)
In the circuit model, id , iq , vd , vq respectively, is the current and voltage of the three-phase stator winding in the direction of the d and q axis. v is linear velocity, Fx is propulsion force, Fload is movement resistant force, m is mass of train, Ld, Lq are stator winding inductances in the direction of the d and q axis, Lmd, Lmq are stator winding magnetizing inductances in the direction of the d and q axis, ψd, ψq are linkage fluxes in the direction of the d and q axis which are as function of currents and inductances in the direction of the d and q axis, La1 is leakage inductance, iF, VF respectively, are the current and voltage of the excitation part of the motor or rotor is located on the bogie of the train and R1 is the active part electrical resistance of the stator, which is calculated in accordance with the following equation [2]:
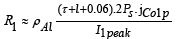 (2)
(2)
That ρAl is specific electrical resistance of aluminum, τ is pole pitch of stator and rotor, l is width of stator stack, PS is number of stator poles in active section of stator, jCo1p is current density of stator winding and I1peak is maximum current of stator winding. MaF is mutual inductance between rotor and stator that is calculated from following equation [2]:
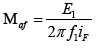 (3)
(3)
f1 is input frequency of three-phase stator winding and f1 is electrical motive force which is calculated from following equation [2]:
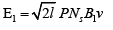 (4)
(4)
P is number of pole pair of field, Ns is number of turn of stator winding per slot of stator, B1 is air gap flux density and v is train velocity.
Inductances, Ld, Lq in relation (1) are expressed as a sum of the leakage inductance with magnetizing inductances. Here the leakage inductance is considered negligible.
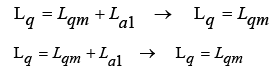 (5)
(5)
Since the magnetizing inductances are dependent on the suspension air gap, therefore, when the air gap of the suspension changes, these inductances also change and they make motor performance is disturbed Consequently, the control objectives for train propulsion will not be achieved. In order to investigate the effect of suspension air gap changes on the propulsion system of the Maglev train EMS, an analytical relationship should be provided between the inductances, Ld, Lq and the suspension air gap. This relationship is expressed for linear synchronous motors with permanent magnet. In the following, reference relations [1] provide an analytical relationship between the magnetic inductance and the air gap for linear synchronous motor with DC stimulation. In the following by relationships of reference [1], an analytic relationship between magnetizing inductances and air gap Suspension for Linear Synchronous Motor with DC excitation is presented.
With respect to relation (1) and with placement ψd ,ψq in the nominal model’s linear motor, we have:
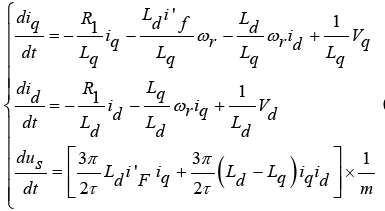 (6)
(6)
The equation related to excitation section or rotor is not used for propulsion control, because this section is used to control the suspension air gap. When the suspension air gap deviates from its desired value, it causes deviation in the electrical current of excitation section from its working point. The variation in the amount of excitation section electric current also causes disturbance in the propulsion system.
Modelling Magnetizing Inductances Ldm, Lqm for linear Synchronous Motor with DC Excitation
In this section, we calculate the magnetizing inductance between rotor and stator distributed windings. For this purpose, Figure 2 is considered which consists of a stator and rotor. As seen in the figure, first, a small element on the stator is considered to be length dxm. If width of stator is l, area of element surface is dxm. l Flux through the surface of this element is expressed following for dxm:
Φ(xm)= B(xm).l.dxm (7)
The winding distribution function ws(xm) describes the number of times a winding s (stator) is connected to the flux in the position xm . So the amount of flux produced by the winding s and the flux passing through element shown in Figure 2 equals ws (xm).B (xm).l.dxm. By integrating the flux passing through the stator surface element over the stator, we have:
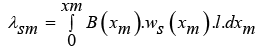 (8)
(8)
The air gap flux density produced by the winding r (rotor) is described as follows:
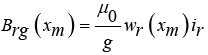 (9)
(9)
By placing the relation (7) in (6) we have:
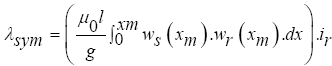 (10)
(10)
In accordance with relation (11) for the mutual inductance between two rotor and stator windings in a linear synchronous motor, we have:
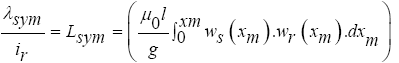 (11)
(11)
The relation (11) is valid for both the self-inductance and the mutual inductance between two windings. To determine self-inductance, we put relation s=r in the above relation.
Relationship (11) is obtained by applying several estimates. These estimates are due to two simplistic assumptions. The first assumption is that the flux density of the air gap is assumed to be uniform in air gap. The second assumption is the effect of slots on the magnetizing inductance which is not considered. In three-phase synchronous machines the winding function is expressed as a function of the stator's electric position:
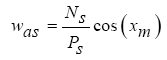
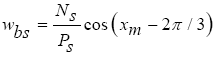 (12)
(12)
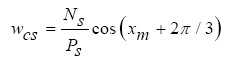
Nsare number of stator winding turn per slot, Ps is number of stator pole, xm is the electrical position of the device relative to a fixed reference in the stator.
If we put r = s = a in relation (11), also, using the winding function of phase a according to relation (11) for a synchronous motor, selfinductance of phase a winding, the following is obtained:
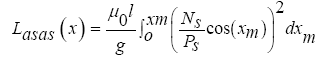 (13)
(13)
By solving the integral of relation (13), the self-inductance for the phase a winding is obtained as a function of the suspension air gap as follows:
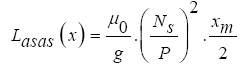 (14)
(14)
In synchronous motors with rotors with non-salient poles, such as rotary synchronous motors with cylindrical rotors, the value of the inductance in the two directions d and q is equal. On the other hand, the magnetizing inductances of synchronous motors are generally expressed as follows:
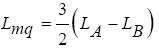
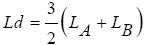 (15)
(15)
If the two relations in relation (15) are put together equal, we have:
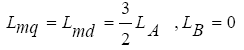 (16)
(16)
On the other hand, generally, for synchronous motors we have:
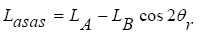 (17)
(17)
θr is angular position of the rotor relative to the stator. By comparing relation (17) with equation (14) the LA for linear synchronous motors is obtained as follows:
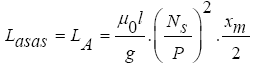 (18)
(18)
Therefore, the Ldm and Lqm for the linear synchronous motor is obtained as follows:
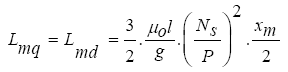 (19)
(19)
According to the linear synchronous motor model in relation (1), air gap variations cause magnetizing inductances and current if deviate from their working points.
In order to linearize the nonlinear equations of the motor in relation (6), the Taylor series is used. Since the behavior of the system around the working points is linear, the relation must be linearized. In linearization, it is assumed that the variations of state variables and system inputs are much smaller than the nominal conditions. Therefore, it is easy to ignore the high order terms.
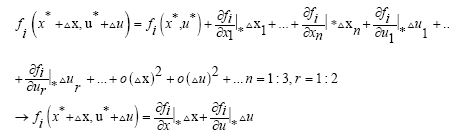 (20)
(20)
Therefore, with respect to relation (21) the state equations of the linear synchronous motor can be linearized around the working points as follows:
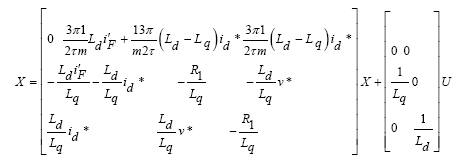
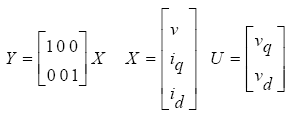 (21)
(21)
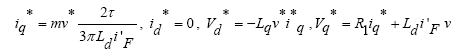 are working points.
are working points.
According to the reference results, linear control can be effective in controlling the propulsion system. On the other hand, because of high interference in the propulsion system, the high gain PI controller has been used. Application of this design is in high performance systems. In this section, the high-gain multi-variable controller is designed to control the speed of the train and the stator current in the direction of the d-axis. The design of this controller is based on the first Markov parameter of multi-variable system. Multivariate systems whose first Markov matrix has full rank, Regular multivariate systems are called. And otherwise they are calling irregular. If the system is regular; the PI controller will achieve its best performance. And in case of system irregularity, an internal feedback is needed to apply the controller. In this case, in addition to the output feedback y (t), an internal feedback Mx1 (t) is used. In this case, according to the Figure 3, the new output is obtained as follows:
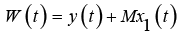 (22)
(22)
If tracking step inputs is desired, assuming the stability of the closed loop system, we have:
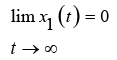 (23)
(23)
The relation (22) shows that the output defined will be equal in steady-state condition with the actual output.
With regarding the relation (21), the matrices in the form below: A, B, C, D, A11, A12, A21, A22, B2, C1, C2 are obtained in the form below:
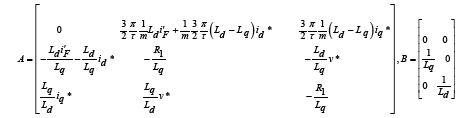
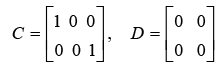 (24)
(24)
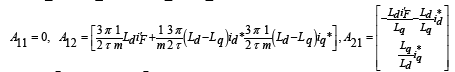
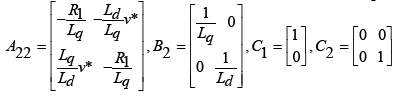
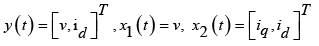 (25)
(25)
By taking into account the equations of the state space of the relation (24), (25) the relation (22) can be written as follows:
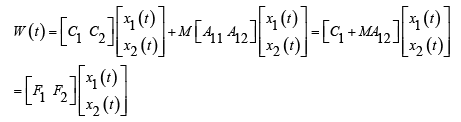 (26)
(26)
In this case, by choosing the measurement matrix M appropriately, it can be guaranteed that F2 have a full rank.
By the placement of relation z (t) = r (t) − y (t) in (21) and the definition z (t) = r (t) − y (t) the equations of closed loop system shown in Figure 3, are obtained as follows:
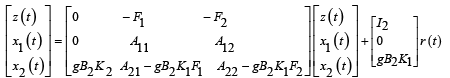
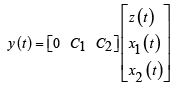 (27)
(27)
For simplicity, the relationship (27) is rewritten as follows:
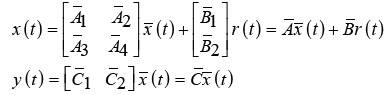 (28)
(28)
In order to analyze the performance and stability of the system, we have to transform the equations (28) into a block-diagonal form. For this purpose, the transformation matrix is
Considered as follows:
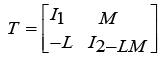 (29)
(29)
So that:
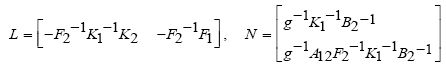 (30)
(30)
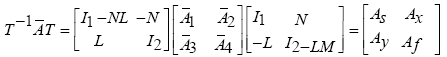
Where in:
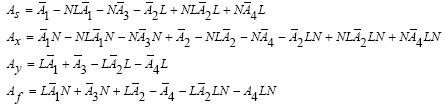 (31)
(31)
To have a block diameter system and to be able to easily analyze the stability and performance of the system based on the elements of the main diagonal, based on (31)
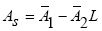
By multiplying the matrix N from the right in the relation Ay in relation (32) and By multiplying the matrix N from the left in the relation Ay in relation (32) and by placement them in relations As, Af are obtained as follow:
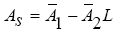
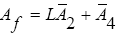 (33)
(33)
Therefore, applying this transformation, the equations are block - diagonal for g→∞
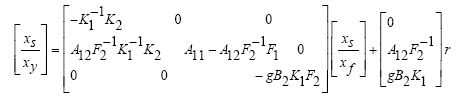
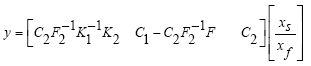
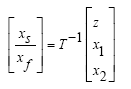 (34)
(34)
Poles of Closed loop system are obtained from matrices on the diameter of the blocked state matrix. In this case, there are three groups closed loop poles with the following characteristics: The first group of poles is an uncontrollable that is given by the following equation:
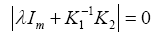 (35)
(35)
Which will remain stable with choice K2 = -αK1
The second group of poles is the slow poles of the system given by the following equation:
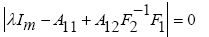 (36)
(36)
These poles are observable due to internal feedback. Also, these poles are new transition zeros that have been created by forming the output W(t). Due to the observability of these poles, they affect the input-output behaviour of the system and slow down the response. The third group of poles is the fast poles of the system and are obtained from the equation:
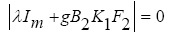 (37)
(37)
Where in 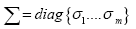 and σi ∈ R+. These poles are controllable and observable, and with selecting K1 as (38) they are placed -gσi for I = 1,2,…,m.
and σi ∈ R+. These poles are controllable and observable, and with selecting K1 as (38) they are placed -gσi for I = 1,2,…,m.
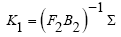 (38)
(38)
To calculate the control coefficients, according to (38) and relation (26), the matrices 2, FM must first be computed.
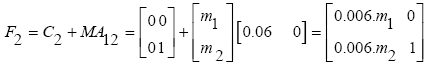
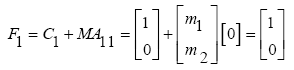 (39)
(39)
m1, m2 should be selected in such a way that according to (38), F2 has the full rank. Therefore, for simplicity in calculations, the element m2 of the matrix M can be considered to zero. So the matrix F2 is obtained as follows:
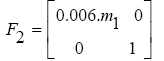 (40)
(40)
The value of m determines the transmission zero of the system. Given the relation (36), the transition zero is as follows:
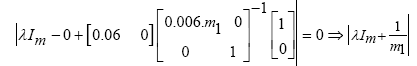 (41)
(41)
By selecting m1 = 0.1 the new transmission zero will be placed in λ = -10. Therefore, the matrix of measurement is obtained as follows:
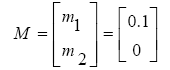 (42)
(42)
So the matrix F2 is obtained as follows:
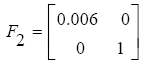 (43)
(43)
According to the principles of PI controller design for multivariate systems, the control coefficients here as the control matrix are as follows:
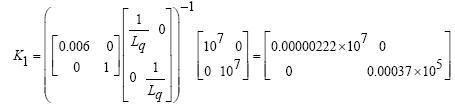 (44)
(44)
Assuming α = -10, the matrix K2 will be obtained as follows:
K2 = -10× K1
Therefore, the PI control law is obtained as follows:
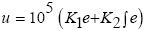
The simulation was done in MATLAB software Simulink. Simulation results include train speed, stator current in direction axis d current, stator three-phase current and stator three-phase voltage (Table 1).
| Parameter | Parameter value | Parameter | Parameter value | Parameter | Parameter value |
|---|---|---|---|---|---|
| m0 | 4p´10-7 | Ns | 1 per slot | ps | 311 |
| g | 9.8 m/s2 | us | 140 m / s | jCo1 p | 4 A/ mm2 |
| L | 1.6 m | B1 | 0.959 T | I1 peak | 1200 A |
| p | 75 | rAL | 2.82´10-8 W.m | La1 | 0 T |
Table 1: Parameter values for the Transrapid 07 Maglev train.
As shown in Figure 4, the linear controller PI has been able to follow the initial conditions of zero as well as the desired optimal velocity profile with a maximum error of 0.0987. The speed profile reaches 140 m/s at 140 s at acceleration of 1 m / s2. It then moves at a constant speed for a period of 400 seconds. At the end, with the acceleration of -1 m / s2 will reaches zero velocity? (Figure 5).
The PI control system has nearly zeroed this current. In the acceleration stage, which ranges from zero seconds to 140 seconds? As the train speed increases, the stator current increases along the axis d. When the train reaches a constant speed in 140s, this current decreases. In the braking phase, which is 540 seconds to 680 seconds, this current increase and there be an increasing trend until the end of the braking time? After 680 seconds, due to zero speed, this current also decreases (Figure 6).
The amplitude of the stator current has increased at the acceleration stage and in the braking stage. But in the constant velocity phase, the range of the three-phase current has declined. The stator input voltage is also three phases. In the acceleration and braking phase, it has large amplitude, but at a steady speed stage it has a smaller range (Figure 7).
If a passenger moves on a bogie, the total weight of the bogie stays constant, but the moment of inertia changes. If it is assumed that a few passengers, whose total mass is 200 kg (Approximately 10% of the bogie mass and cabin mass), will move on a bogie, the effect of its movement is considered as the disturbance moment of inertia and disturbance torque in the following figures (Figures 8 and 9).
By applying these disturbances to the closed loop control system, the controlled air distance is obtained as follows: (Figure 10).
As shown in the figure above, the movement of passengers on the train creates a disturbance in the moment of inertia and creates a disturbance torque, which results in disturbance in the suspension air gap (Figure 11).
Due to disturbance at the suspension air gap, the suspension current is increased or decreased from the its working point value to compensate for the difference in suspension air gap from the reference value of one centimeter. Oscillations in the figure are the result of this compensation. By applying the results of the suspension air gap and suspension current, the results of the propulsion system controller are obtained as follows: (Figure 12).
In the figure above, the linear controller has not been able to reduce the effects of the deviations of air gap suspension on the speed of the train, causing ripples at the speed of the train (Figures 13 and 14).
The results obtained in the figure above show that the stator current in the direction of the d-axis is affected by disturbances. The oscillations of the disturbance in the figure have a very small range. So it can be said that id closely follows the zero reference value. The closed loop linear control system PI cannot robust for the parameter variations due to the disturbances moments. For this reason, it causes unwanted fluctuations with high amplitude in the current and voltage of the three-phase stator (Figures 15 and 16).
The suspension system has an impact on the propulsion system electrically and electromagnetic. These effects are done respectively through the electric current of the suspension system electromagnets and suspension air gap. When the suspension air gap the due to disturbance deviates from the desired value of 1 cm, current of suspension electromagnets in order to setting suspension air gap also deviates from working point. The magnetizing inductances also change and cause the uncertainty in the propulsion system. The simulation results showed that the designed controller can compensate for the disturbance effects of the suspension system on the propulsion system, but when this disturbance affects, more increase in the propulsion system ,causes oscillation in the stator current and voltage and train speed.