Journal of Ergonomics
Open Access
ISSN: 2165-7556
ISSN: 2165-7556
Research Article - (2016) Volume 6, Issue 3
Life for a foot soldier frequently involves marching while wearing a uniform, boots, and interceptor body armor vest (IBA) and also carrying a backpack and rifle. Additionally, soldiers may traverse various terrains from smooth to rough, from vegetated to barren, from steep inclines to varying angles of cross slopes. The study presented here is new and unique. It determines the lateral stability of a person walking along a cross slope using a formula which is based on the inverted pendulum. Those who participated in this study walked along cross-slopes (0, 5 or 10 degrees) while wearing backpacks loaded at various levels (low, middle or high). The final results of this particular investigation, however, indicate that neither load position nor cross-slope angle produced significant effects for lateral stability within an alpha of 0.05 for the participants accustomed to backpacking.
Keywords: Battlefield; Hazardous occupation; Pelvis
Working in the military is by nature a hazardous occupation. It requires a soldier to risk life and limb to combat enemies under various conditions. One of the enemies, however, of the United States soldier is not restricted to the battlefield. In the United States’ war history noncombat casualties have resulted in more hospitalizations and lost persons-time than all combat casualties combined [1]. Such injury issues have an impact on the mission of the military. As such these are a cause for further study and effort.
One source of non-combat injuries experienced by ground force personnel is falling down. In some cases falling down may be attributed to loss of balance from wearing a heavy backpack [2-4]. Influencing the effect of the backpack on the soldier is its weight. Soldiers in the field may carry backpacks weighing as much as 54 kg (120 lbs) [5] or more [6]. Yet, even packs that weigh under the maximum recommended fighting load of 22 kg (49 lbs) or about one third of the soldier’s body weight) [6] are said to adversely affect a soldiers stability [2].
Besides weight, two other aspects of carrying a backpack may affect stability and therefore increase the risk of falling. These are the load location within the backpack and the terrain traversed while carrying the pack. Load location defined here is where the centre of the backpack load mass is vertically located; whether it is near shoulder height, the middle of the back or low down near the lumbar region. The terrain a soldier must traverse, as mentioned above, varies. Walking surfaces such as hard, sandy, canted, sloped, slick and uneven present a few of the types of terrains the soldier encounters [6,7]. The terrain specifically studied here, though, will be a cross-sloped terrain of varying angles such as that encountered along the side of a road or parallel to a mountain range. These will be treated here as level ground, 5 or 10 degree slopes.
Authors of various studies have theorized which location in a backpack is best suited for loading. Some have suggested that setting the load mass at the highest location has an advantage that it takes less forward tilt of the back to bring the center of the backpack load closer to the body’s vertical center of mass [8,9]. Talbot indicates in her study that the higher location results in less sway which is indirectly related to more stability [4]. Some researchers, however, say the lower placed loads make it less likely that balance will be compromised in contrast to more top heavy higher placed loads [10].
A particular combination of backpack loading center for a crosssloped walking terrain may provide the most stable condition for the typical soldier [9] (Figures 1 and 2) and should be identified to improve the soldier’s well-being.
The purpose of this study is to investigate combinations of backpack load locations and hard surface cross-sloped terrain which may prove the most stable to service member backpackers. It is best to measure these conditions using actual walking trials as these are notably different from static trials [11].
To test the effect of backpack loading on level and cross sloped surfaces (5 and 10 degrees) recruits were sought who were able to wear and walk with a backpack, helmet, simulated IBA and rifle which amounted to a total weight of 36.5 kg.
Though the announcement was displayed at the University of Utah campus and available to everyone who met the qualifications, all volunteers came from the military Reserve Officers' Training Corps (ROTC) groups (Army and Air Force) on campus or from Army Reserves. A total of 15 participants were able to attend the testing before equipment requirements expired. These participants walked with the defined loads under the various conditions described in order to evaluate their stability. They were also given surveys to assess their responses to walking with different backpack load placements on various cross-sloped angles.
The concept for initiating the trials performed in this study suggested that the backpack loading position would affect the stability of the wearer according to the cross-slope travelled.
Hypothesis 1: the null hypothesis for this study is there is no significant difference in the stability of a person, who is wearing a backpack, regardless of the interaction between the backpack load location (whether at a location low, middle or high on the back) and the angle of cross-slope (whether a level surface or tilted at 5 or at 10 degrees) being traversed by the person.
Hypothesis 2: the null hypothesis for this study indicates there is no significant difference in the stability of a person, who is wearing a backpack, regardless of the main effect of cross-slope degree (whether on a level surface at 5 degrees or at 10 degrees).
Hypothesis 3: the null hypothesis for this study indicates there is no significant difference in the stability of a person, who is wearing a backpack, regardless of the main effect of backpack load position (whether at a location low, middle or high on the back).
In order to quantify the stability of an individual carrying a heavy backpack along a level or cross-sloped surface, an adjustable track was set up at the University of Utah Ergonomics and Safety Laboratory in the Merrill Engineering.
Participants and Materials
Participants were requested by announcements on the University of Utah campus. Eligible people were to be between the ages of 18-50, the heights of 153-193 cm (5’0” to 6’4”), and the weights 48-91 kg (105 lbs-200 lbs). 15 eligible people (11 males and 4 females) participated (Table 1). These individuals were either currently members or officers of the Army ROTC or Air Force ROTC programs on campus or involved in another military program (in the Army Reserves) and had experience carrying backpacks of the weights used in the study. Each participant signed a consent document verifying their voluntary participation in this study. They were reminded that at any time they could choose to stop testing. Participants were compensated for their time.
| Gender | Height in cm | Weight in kg |
|---|---|---|
| M | 183 | 78.5 |
| M | 175 | 75.2 |
| M | 173 | 63.9 |
| F | 161 | 57.6 |
| M | 182.5 | 76.7 |
| M | 192 | 74 |
| F | 164 | 57 |
| M | 173 | 76.5 |
| M | 184 | 71.5 |
| M | 186 | 74.5 |
| M | 168 | 70 |
| F | 174 | 54.5 |
| F | 167.5 | 60.5 |
| M | 174 | 83.5 |
| M | 179 | 84.5 |
Table 1: Gender, heights and weights of volunteers.
The result, for a power of 0.95, was to test here with a sample size of at least 7 (determined from a study as close in nature as available). More than twice that number were desired, but due to lack of volunteers only 15 eventually agreed to participate.
Personnel equipment
Personnel markering: Each participant had small reflective marker balls attached to them at specific locations on their bodies. These locations were the same for each participant and represented the landmarks of shoulders, elbows, wrists, and so on until all appropriate landmarks were identified along with the backpack and dummy rifle. By using the reflective markers each body segment was defined to the computer system and provided information for determining the overall center of mass for the participant and additional weights.
Personnel apparel: Participants were asked to wear tight fitting biker shorts, a tank top shirt, and military style boots. The smallest boots available were too large for one particular participant so alternative foot wear was used, Since no significant outliers were determined by final analysis the change in footwear for this participant was not appreciable and the data used.
Additional weights on personnel: To mimic the marching foot soldier, participants were asked to wear and carry additional items to those noted above, which added s36.5 kg of additional weight on their person.
Participants donned a weighted (at 11.6 kg) vest (to simulate Interceptor Body Armor (IBA)), an Army helmet (1.8 kg) and carried a dummy rifle (3.1 kg). These extra items were requested to be included by the committee member of this study who is an officer and professor in the Army ROTC program at the University of Utah campus.
Finally, a backpack (with shoulder straps and a hip belt) was put on and adjusted for each participant. This backpack was a modified MOLLE backpack (Figure 1). It was created using the exterior frame of a MOLLE fitted with two rails where-on the load could be moved vertically.
As can be seen from Figure 1, the path of the load adjustment was kept in line with the wearer’s torso when straight (comparing the red line with the rails in Figure 1). The horizontal location of the center of the adjustable load was 0.125 m from the back of the participant. The top, or high, location of the load placed the center of the load approximately even with the shoulders. The bottom, or low, position of the load placed its center approximately even with the bottom of the spine. The middle location is equally distant (0.23 m) from the top and bottom locations.
The weight of the weighted vest, the rails and the backpack support (excluding the movable load) accounted for the weight and distribution of an actual IBA.
Track equipment
The track was a 7.3 m long, 0.9 m wide raised wooden track. The track was adjustable so it could be tilted using hand jacks from level to 10 degrees as shown in Figure 2 (participant is walking back from.l trial on track all trials were performed walking the opposite direction from the person in Figure 2). Note that the maximum track angle of 10 degrees was deemed to be at the maximum of what was considered safe for the participants. Any further tilt would be considered a slipping hazard (which was noted at one point during a 10 degree cross-slope trial with one participant until the force plates were adequately cleaned).
Test Procedure
Using a formula (Formula 2-1, presented later in this report) as a basis for determining lateral stability, the process described below was established. Participants were prepared and equipment set up as follows.
Prior to testing
Each participant reviewed and signed a study consent form and was assured any feelings of discomfort needed to be reported and resolved or the testing stopped. Participants were weighed and their heights measured for use in the software for computer modelling. Each participant was given a unique number to keep their personal information secure.
Static capture
Participant static capture: Participants were asked to stand in the middle of the motion capture image zone for a short time (approximately 6 s) while they were videotaped. This allowed the program to identify the body landmarks, as well as the backpack and rifle (in the program the helmet and vest were treated as part of the head and thorax with additional weight added to the respective body parts to account for their presence) necessary to establish the body segments and determine the entire center of mass (CoM) for the person and load.
Force plate static capture: The force plates were also marked to orient the motion capture system to the plates. In this way the participant and plates could be merged into one record and the coordination of the participant stepping motion onto the force plates could be synchronized with the associated forces involved.
Dynamic capture
Participant dynamic capture: After static calibration some of the markers were removed from the participants to make their movements less restrictive (though the program was still able to track their dynamic movements with the remaining markers). They were then asked to walk along the track at a randomly selected angle (0, 5 or 10 degrees) wearing the backpack which was set at a randomly selected load position (low, middle or high back location). All the load positions were tried before the track was set at the next random degree. For each condition (nine in all) the participant performed it at least four times before moving to the next condition. The participants were asked to follow small flags fixed to a loop of moving string next to the track at 4 km/h to keep the walking pace consistent. The left foot was assigned to land only within the first force plate and the right foot the second.
The set up described above allowed the measurement of each of the variables identified in Equation 2-1 below. By using the formula a value “b” was derived for every combination of the track angle and load position for each participant subject. These “b” values were then used in a two way (for both angle and position) random measures analyses to identify any significant effects.
Formula
Walking stability has been described by one author as a state of “not falling down” [12]. Another author defined dynamic stability as “the capacity to move the body segments in a coordinated fashion [13]. Still another author used stability to describe a relative condition - a person who is walking is considered more stable in one circumstance than another if the same external influences on the first person creates less of a perturbation effect than that of the second [14].
The measurements used in this study were evaluated based on modelling human balance as an inverted pendulum.
The measure of stability given here is not a set value having a definite numerical standard, but rather is a relative term of comparison. A person experiences increased stability as they are better able to resist being “knocked off balance” by external perturbations. During standing, stability is greatest when the center of mass (CoM) is furthest from the perimeter of the body’s area of support. This supporting area is on or within the outer edge of the body’s base of support (BoS, or outer area of foot to floor contact Figure 3) and its center is referred to as the center of pressure (CoP).
Figure 3: Illustration of variables [14].
An analogous scenario of greater stability in one case over another would be the increased difficulty of tipping over a cone (point up) with a large diameter to a cone (point up) of a smaller diameter of the same height. The larger diameter cone is relatively more stable than the smaller diameter cone because it would be harder to tip over.
This stability value is expressed in terms of a distance. In the cone example the large cone radius represents the stability value to be compared to the small cone radius.
An additional factor affecting stability is the inertia of the object’s mass tending away from the center-point of support. If, in the cone example, the cone already had some momentum toward the side to which it would be tipped, it would be less stable than when it was static. This is considered its dynamic characteristic. Consequently, when a standing person starts to lean they become less stable and must adjust to remain standing.
Using these concepts the method of mathematically quantifying the degree of stability can be developed from the following stability formula by Hof [14] (Equation 1):
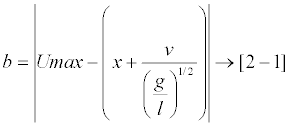
Where “b” represents the closest distance between the ‘dynamic CoM’ (or XCoM, represented by “x + v / (g/l)½”) and the border of the BoS which is described by “Umax”. Note that in this case the CoP is between the Umin and Umax shown in Figure 3.
Note that the “x” represents the instantaneous vertical point of the CoM and the “v / (g/l) ½”portion represents the inertia of the center of mass in terms of length. This formula is based on modeling the body movement on an inverted pendulum, which is why the value “(g/l)½” is employed (Hof, et al, re-identified the value “(g/l)½” as “ω”).
Though Figures 2 and 3 illustrates the standing stability of Equation 1 in the sagittal plane, the formula will be used in the frontal plane (laterally) for walking. The factors for the CoM, CoP and a lateral velocity of the CoM are usable for the walking situation specifically when the on-stepping foot is fully supporting the body, just after the off-stepping foot is raised. Walking is notably different than static standing because when the person is walking the BoS changes with each foot lift and subsequent placement. Consequently the BoS area in the walking case is not used, but rather the instant point of contact pressure of the foot towards which the CoM is traveling. The image which might be used to clarify this idea is a ballerina on point. She is more stable after she establishes the toe onto which she is going to rise, just before she rises, than after she lifts off her supporting foot. So too the least stable lateral point of walking is when the heel has struck for a new step and the center of mass is tending toward it with the other foot lifted from the ground (personal communication from At Hof).
As noted before, in most cases, the telling indicator of stability is how perturbations affect the maintenance, or recovery of, the erect body, which is determined by the size of “b,” or the difference between the XCoM and the CoP. The greater the value of “b” the better the stability. Again, this is assuming the XCoM is headed toward rather than away from the CoP. If the XCoM is moving away from the CoP, instability has already begun and a new CoP must be established ahead of the XCoM [14] to maintain stability.
As in the example of the cone, it could be theorized that the lower backpack weight location should prove to be the most stable in all conditions. It has been reported from experience of hikers, however, that the high location is easiest to carry on level ground.
Considering this and the suggestion of others that low is better for unstable terrain, it may be that the pack weight location is variable depending on terrain, and the high pack is best for level [9], the low pack is best for higher cross slope and consequently the mid-pack placement is best for terrain which is somewhere in between.
Stability data
A concerted effort was made to provide complete results for each participant with all four runs per condition. However, this was not obtainable. Either camera identification of essential markers was lost or other recording challenges occurred. Consequently, the data from the runs of each condition were averaged to produce one “b” value per condition per participant. These were then analysed using the two way repeated measures method of the Statistical Package for the Social Sciences (SPSS) program with an alpha of 0.05.
Survey data
The results of the surveys were also analyzed and the results determined. The participants were given a survey which requested them to fill in a Likert Scale according to the following, “Compared to not wearing any load please rate how hard it was to walk with total load.” For each of the nine conditions of backpack load position and cross-slope angle the questionnaire had five levels to choose from namely: very easy, somewhat easy, neither easy nor hard, somewhat hard and very hard.
Results
Analyses of stability: Stability measurements were taken of each participant when they were on their left and also on their right foot at the various side sloping angles and backpack locations.
For the left foot data analysis no outliers were discovered with studentized residuals that were greater than ±3 standard deviations.
Normality values showed that two of the conditions were below 0.05 and therefore not normal. However, since the rest were within normal values disparity was not considered critical. To further test this, however, analysis was performed with a square root data transformation. Results produced more normal values, but final values still did not show significance.
Mauchly’s test of sphericity showed suitable values for use of the two-way repeated measures analysis χ2 (9)=0.334, p=0.254.
Table 2 shows the comparison of left foot stability values between the nine various conditions to determine whether there were any significant differences. A two-way repeated measures analysis was performed for these values with the following results (tests of withinsubjects effects):
| Source | Type III | df | Mean | F | Sig. | Partial Eta Squared |
|---|---|---|---|---|---|---|
| Sum of Squares | Square | |||||
| Degrees | 0 | 2 | 5.13E-05 | 0.506 | 0.609 | 0.04 |
| Error (degrees) | 0.002 | 24 | 0 | |||
| Position | 0 | 2 | 0 | 1.946 | 0.165 | 0.14 |
| Error (position) | 0.002 | 24 | 6.70E-05 | |||
| degrees * position | 0 | 4 | 5.12E-05 | 1.039 | 0.397 | 0.08 |
| Error (degrees*position) | 0.002 | 48 | 4.93E-05 |
Table 2: Two-way interactions of angle and position at left foot.
There are no significant two-way interactions between cross-slope angle and backpack load position at left foot F (4,48)=1.039, p=0.397>0.05, partial η2=0.080. Nor did the main effects of degree, F (2,24) =0.506, p=0.609>0.05, partial η2=0.040, or position, F(2,24) =1.946, p=0.165 > 0.05, partial η2=0.140, show significance.
For the right foot data analysis no outliers were discovered with studentized residuals that were greater than ± 3 standard deviations.
Normality values for this foot also showed that two of the conditions were below 0.05 and therefore not normal. However, since the rest were within normal values the disparity was not considered critical. To further test this, however, analysis was performed with a similar data transformation to that of the left foot without test significance.
Mauchly’s test of sphericity did not provide support for the right foot interaction of degrees and position sphericity, χ2 (9) =0.096, p=0.004, so Greenhouse-Geisser adjustments were chosen to be used for all right foot analyses: 0.902 for degrees, 0.838 for position and 0.486 for the degrees*position interaction.
Table 3 shows the comparison of right foot stability values between the nine various conditions to determine significant differences. These were also analyzed using a two way repeated measures analysis (test within subject effects).
| Source | Greenhouse-Greisser value | Type III | df | Mean | F | Sig. | Partial Eta Squared |
|---|---|---|---|---|---|---|---|
| Sum of Squares | Square | ||||||
| degrees | 0.902 | 0 | 1.803 | 0 | 1.573 | 0.23 | 0.116 |
| Error (degrees) | 0.002 | 21.64 | 0 | ||||
| position | 0.838 | 0 | 1.676 | 6.53E-05 | 0.537 | 0.562 | 0.043 |
| Error (position) | 0.002 | 20.112 | 0 | ||||
| degrees *position | 0.486 | 0 | 1.944 | 7.96E-05 | 0.857 | 0.435 | 0.067 |
| Error (degrees*position) | 0.002 | 23.322 | 9.29E-05 |
Table 3: Two-way interactions of angle and position at right foot.
There were no significant two-way interactions between degrees and backpack load position at right foot F (1.944, 23.322) =0.857, p=0.435>0.05, η2=0.067. Neither did main effects of degree, F (1.803,21.64) =1.573, p=0.23>0.05, η2=0.116, or position, F (1.676, 20.112) =0.537, p=0.562>0.05, η2=0.043, show significance.
Analysis of Questionnaire
The surveys showed an overall sense, on average from the participants, that carrying the backpack was between “somewhat easy” and “neither easy nor hard”.
The statistical analysis of the survey indicates that participants believed the cross-slope at 0 degrees (level) was easiest, as expected. The middle backpack location was also noted as being easiest at all slope angles (Table 4).
| Cross-slope Degree | Load Position | Very Fast | Somewhat Easy | Somewhat Hard | Very Hard | Average Easy | Average hard | Easy-hard | Sum of Degrees | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 Degrees | High | 3 | 7 | 2 | 0 | 5 | 1.5 | 3.5 | **8.5 | ||||||||||
| 0 Degrees | Middle | 4 | 5 | 6 | 0 | 4.5 | 0 | *4.5 | |||||||||||
| 0 Degrees | Low | 2 | 3 | 6 | 0 | 2.5 | 2 | 0.5 | |||||||||||
| 5 Degrees | High | 3 | 6 | 0 | 0 | 4.5 | 3 | 1.5 | 4 | ||||||||||
| 5 Degrees | Middle | 2 | 5 | 8 | 0 | 3.5 | 0 | *3.5 | |||||||||||
| 5 Degrees | Low | 2 | 3 | 3 | 0 | 2.5 | 3.5 | -1 | |||||||||||
| 10 Degrees | High | 2 | 3 | 6 | 2 | 2.5 | 2 | 0.5 | -0.5 | ||||||||||
| 10 Degrees | Middle | 1 | 4 | 7 | 0 | 2.5 | 1.5 | *1 | |||||||||||
| *Highest load position ratings for the easiest carry at the various cross-slope angles ** Highest easy cross-slope angle (the highest average score for degrees was at 0) |
|||||||||||||||||||
Table 4: Questionnaire results for ease of backpack at different positions and angles.
The indications from this study support the null hypotheses that backpack load location does not have a significant effect of the lateral stability of the carrier when walking on various cross-sloped angles from 0 to 10 degrees, whether interactions or main effects of degree and angle are considered (supporting null hypotheses 1-3).
This study was performed on a cross-slope maximum angle of 10 degrees on a continuous hard surface. The value of testing a person in this condition was repeatability and consistency. The results showing that neither position nor angle significantly affected the stability of the participant were not expected.
A possible reason for lack of significant lateral stability differences is the eligible participants were somewhat seasoned in backpacking, having experience marching with standard loads [10,15].
Additionally, it was requested the participants carry a dummy rifle, which, though it adds weight, may in field conditions have a balancing influence as the walker moves the mass of the rifle to achieve more stability, though if the arm swing is restricted (as it was in the current study) rifle carry may increase instability [16]. The participants were instructed to hold the rifle away from their bodies so the motion capture markers could be seen by the motion capture cameras. They were also directed to hold the rifles somewhat still in respect to their bodies possibly influencing each combination.
The difference in stability did not significantly change (within an alpha of 0.05) for either foot between any of the conditions. This implies that the body adapted to the cross-slope and load position changes in such a manner as to maintain nearly the same stability values throughout the trials (whether walking on a level surface, at a 5 degree or a 10 degree cross-slope). Part of the reason for this may be the body’s innate compulsion to maintain the torso in an upright posture, with the head taking precedence and the eyes maintaining a horizontal view [4]. In this respect the pelvis is not tilted to the same degree as the cross-slope and is more level, helping to keep the torso upright. However, even though the pelvis does not tilt to the same angle as the cross-slope (as determined from samples of the participant walks) there is a slight tilt toward the down slope foot [17]. Consequently, when the pelvis tilts it moves the center of mass slightly more in the direction of tilt as the torso remains vertical. This may help move the center of mass toward this foot, allowing the overall stability to remain constant between the ranges of 0 to 10 degree cross-slopes (Figure 4).
This manoeuver may match the type of changes that occurred in legs and ankles from Dixon and Pearsall’s study [17] of walking on a 6 degree cross-slope. In their study the up side limb length was functionally shorter at 80.0 ± 2.8 cm and the down side length was longer, at 81.4 ± 2.8 cm, for the participants. In the Dixon and Pearsall [17] study this was achieved in part by increased dorsiflexion in the up slope foot and decreased dorsiflexion in the down slope foot. In addition, however, the ankles rotated in the lateral plane to accommodate the cross-slope, and during toe-off the up slope leg was in closer to the body (more adducted) while the down slope leg was further away (more abducted). Thus the feet and center of mass may have moved equivalently (Figure 4).
All of these changes would need to be quantified to determine the exact body movements which produced consistent stability results in the lateral plane according to the formula by Hof (Equation 2-1).
Though widening the step width may increase stability [18] the reverse may not be true in the sense that it may be that there is a minimum acceptable stability a body allows in order to proceed at a given rate in forward motion. Support for this concept is noted by Hof et al. [19]. In their study report they explain that lateral perturbations are resolved by maintaining a fixed “b” distance (reference Equation 3-1 for “b”). Lateral stability is actively controlled by humans [20] and this control may dictate a set stability limit, one to which a healthy individual is accustomed and to which an able body will adapt whether on level or angled cross-slopes or even with additional loads loaded in various locations on the back.
Comparison to similar studies
No specific studies have been done on the stability of walking along various cross-slopes with differently positioned backpack loads. A best comparison can only be made to studies which examined the difference in walking stability of wearing a backpack load at various vertical locations on a level surface.
The vertical position of the load was determined by some authors to be more stable in a higher location [4] while others supported lower placed backpack loads [12,21,22]. Additionally other authors indicated that load placement stability depended on the terrain [9].
Limitations of this study
There are several issues affecting the outcome of this study. The study population had training in backpack wearing, the sample size is limited, and not all four trial runs of the data sought were consistently available. It is proposed, however, that, while the results were obtained from sound data (no influential outliers), there still are additional areas of investigation worth considering.
Recommendations for future study
One such future consideration is to perform the study with a larger and more diverse group.
Another area to review is to consider greater loads to test to match more closely the current field experience of soldiers. The loads included in the study, however, seemed to be close to the maximum for some of the individuals included in this study. It was observed that the weights used were nearly too much for some participants as they struggled to maintain the walking speed specified especially near the end of the trials.
The results of this study show that there are no significant changes in lateral stability due to vertical location of backpack load or angle of cross-slope. This seems to indicate that the body can adapt to differing conditions while maintaining a similar pattern of lateral stability at least for the population participating who are experienced in walking with backpacks of similar weight.