Experts and professionals of communication and electronics background frequently require knowledge on signal analysis and processing. Following the development of advanced instrumentations, some traditional instruments started to develop in the direction of computerization. Virtual Instrument (VI) arises at this historic moment. VI is a kind of instrumentation with extended and user-friendly functions which is widely applicable in many fields such as noise testing [1], bio-signal acquisition [2], the signal process [3], DAQ system [4], digital image enhancement [5], etc. LabVIEW of National Instruments, USA is the most renowned and user-friendly development tools of VI software. With its strong signal processing and analysis capabilities, we have chosen LabVIEW to design a signal analyzing and processing virtual instrument (VI). Utilizing the environment of LabVIEW graphical programming, our developed system can make the users feel more visual in image impression of signal analysis and processing.

Our signal analysis and processing system contain six modules: Spectrum Analysis, Filter, Correlation, Convolution, Modulation, and Fast Fourier Transform. Some major module contains several submodules to extend the scopes and opportunities of the systems as shown in the block diagram (Figure 1). We used several signal analysis function as an example which off course can further be extended as required to introduce the composition of the system.

Figure 1: Operations performable by our system.

Signal processing-spectrum analysis

The power spectral density of a discrete time signal y(t) is defined as:

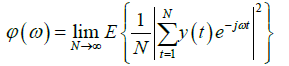
Where φ(ω) is the power spectral density of the signal y(t) [6,7]. We developed a VI for obtaining the spectral analysis of signals. For example the, power spectral density of the multiplication of a sinusoidal and square wave gains the form shown on the virtual monitor below. Using our system one can obtain the spectral analysis of different signal i.e. sinusoidal, square, triangular, saw tooth and so on. The amplitude, frequency, duty cycle and phase of the input signal/signals may be adjusted according to our need. The VI and block diagram is shown in Figures 2 and 3 respectively.

Figure 2: The Virtual Instrument (VI) for obtaining power spectral density.

Figure 3: The front panel showing the spectral analysis of multiplied sinusoidal and square wave.

Signal processing-amplitude modulation and demodulation

Modulation is the process in which we vary a higher frequency carrier wave to transmit information. It is therefore theoretically possible to transmit baseband signals (or information signal) without modulating it. However, it is far more efficient to transmit data by modulating it onto a higher frequency carrier wave. There are some techniques of modulation and Amplitude Modulation (AM) is one of them. Modulation in which the amplitude of a carrier wave is varied in accordance with some characteristic of the modulating signal is known as Amplitude Modulation (AM). A practical example of amplitude modulation is AM radio stations which transmit audio signals ranging from 20 Hz to 20 kHz and with carrier waves ranging from 500 kHz to 1.7 MHz. Figure 4 shows the graphical expression of Amplitude Modulation technique. The amplitude of the carrier signal is varied in proportion to the message signal. A typical message signal can be represented by:

Figure 4: Graphical expression of amplitude modulation.

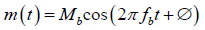
And the carrier signal can be represented by:

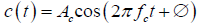
To make the equations simpler, assume that there is no phase difference between the carrier signal and the message signal and thus φ = 0.

The modulated signal can be represented by multiplying the carrier signal and the summation of 1 and the message signal, as shown below

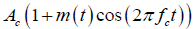
After some basic trigonometric manipulation, the above waveform can be written as [8]:

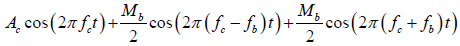
When demodulating a signal, two basic steps should be considered:

1. Creating baseband signal: The main element of AM demodulation is to regain the baseband signal. This can be achieved in a number of ways one of the simplest is to use a simple diode rectifier circuit. The circuit will rectify the modulated signal and the output will appear as like as shown in Figure 5.

Figure 5: Basics of amplitude demodulation.

2. Filtering: The filtering removes any unwanted high-frequency elements from the demodulation process. The signal can then be presented to further stages for signal amplification, etc. [8,9] (Figures 6 and 7).

Figure 6: The Virtual Instrument (VI) for obtaining Amplitude Modulation (AM) and demodulation.

Figure 7: The front panel showing the input and output of an AM wave.

Signal processing-filtering

In signal processing, a filter is a device or process that removes some unwanted components or features from a signal. For example, a bandpass filter allows signals between two specific frequencies to pass and discriminates against signals at other frequencies [10]. A typical input/output of a bandpass filter is shown in Figures 8a and 8b.

Figure 8a: A typical input signal to be filtered.

Figure 8b: A typical output response of a band-pass filter.

We developed a Virtual Instrument (VI) for signal filtering purpose. It is possible to obtain the output response of an LPF, HPF, BPF, BSF, FIR, and IIF. The output response (Figure 9) of a bandpass filter of a sawtooth signal is shown on the virtual monitor.

Figure 9: The front panel showing the Input and output response of a band pass filter.

Signal processing-convolution and correlation

Convolution is a mathematical operation used to express the relation between the input and output of an LTI system. It relates input, output an impulse response of an LTI system as

y(t) = x(t)*h(t)

Where y(t) =

the output of LTI; x(t)

= input of LTI; h(t)

= impulse response of LTI

To compare the similarity of two sets of data we can use correlation. By shifting two signals one after another, similarities are computed. The result reaches a maximum at the time when the two signals match best. If the two signals are identical, the maximum is reached at t = 0 (no delay). Therefore correlation is a good method to measure the delay between two signals having similar shapes but one is delayed in time for the possible addition of noise [11]. We developed a Virtual Instrument (VI) which can be used to perform convolution, autocorrelation, and cross-correlation of signal/signals. The input/output can be observed on the virtual monitor.

Signal processing-fast fourier transform (FFT)

A fast Fourier transform (FFT) algorithm is used to compute the Discrete Fourier Transform (DFT) of a sequence, or it’s Inverse Fast Fourier Transform (IFFT). The Fourier Transform converts a signal from its original domain (generally time domain) to a representation in the frequency domain and vice versa. However, the DFT is mathematically simple and computationally more relevant than the Fourier Transform. An FFT computes such transformations rapidly by factorizing the DFT matrix into a product of sparse (mostly zero) factors. As a result of that, it can reduce the complexity of computing the Discrete Fourier Transform (DFT) from 0 (n²), that arises if one simply uses the definition of DFT to 0 (n log n). Here n is the data size [6]. Utilizing these concepts our developed system can analyze the FFT of a signal by means of virtual instruments.

The front panel of our system consists of three parts: Signal Panel, Control Panel and virtual monitor (Figures 10 and 11). Using signal panel we can adjust the properties of desired input signals i.e. amplitude, frequency, phase, duty cycle, etc. The control panel is used to select different operations i.e. modulation, correlation, FFT and so on. We can also select the desired input signal/signals on which specific operation can be performed. The virtual monitor (Figure 12) consists of input and output graphs from which the input/output response of a selected operation can be observed.

Figure 10: The front panel showing the adjustable properties of different signals.

Figure 11: The front panel showing the signal selectors and operations on the signals could be performed.

Figure 12: The front panel showing the virtual monitor.

The Virtual Instrumentation (VI) platform of signal analysis and processing was designed by LabVIEW which is a graphical programming language and contains many signal analysis and processing functions with user-friendly interfaces. If we compare virtual instruments with other traditional instruments, certain advantages in the level of virtualization, intelligence, processing speed/power, price, operability, etc. can be found. Our developed system has the advantage of flexible operation because optimization can be performed at any instances by the users according to the requirements. Many more virtual signal analysis and processing modules can easily be added because of the openness of LabVIEW. Thus more and more comprehensive application programs can be added to the system to fulfill the needs of the world.