Journal of Proteomics & Bioinformatics
Open Access

DMWAS: Feature Set Optimization by Clustering, Univariate Association, Deep and Machine Learning Omics Wide Association Study for Biomarkers Discovery as Tested on GTEx Pilot Dataset for Death Due to Heart-Attack

Abhishek Narain Singh^{* *}Correspondence: Abhishek Narain Singh, Schiller International University, Heidelberg Campus, Zollhofgarten 1, 69115 Heidelberg, Germany, Email:

Author info »

Background

Genomes of individuals are said to be more than 99% similar. This small variation of less than 1% in the DNA accounts for vast amount of differences in endo-and-end phenotype and behavior of the person. Variations of single letters in nature, such as the letters A, T, G, C, N can be easily encoded, while numerical representation of variations of DNA of more than 1 letter need more complicated and logical methods. GWAS has been used for univariate methods of association of these variations to end phenotype until now [1]. A univariate method for association of the genomic variations with the end-or-endo-phenotype has been widely used through software tools such as snptest [2] and p-link [3]. Methods of multivariate GWAS where there are multiple phenotypes to associate with as dependent variables, which are claimed to perform better, have been suggested [4]. However, these associations still take one independent variable at a time for genome wide association, therefore are less stringent resulting in spurious results. We see lately that overall contribution of these loci to heritability of complex diseases is often less than 10% [5]. A preprint of this paper was published in early 2021 at biorxiv [6]. As pointed out from McCLellan and King, Cell 2010 [7]

“To date, genome-wide association studies (GWAS) have published hundreds of common variants whose allele frequencies are statistically correlated with various illnesses and traits. However, the vast majority of such variants have no established biological relevance to disease or clinical utility for prognosis or treatment.”

“More generally, it is now clear that common risk variants fail to explain the vast majority of genetic heritability for any human dis- ease, either individually or collectively Manolio [1].”

Models where more of the independent variables (here the genotypes) need to be incorporated as means of statistical association of the variants to the phenotype need to be built; addressed here by means of deploying deep learning and machine learning techniques. Of late, there have been several attempts to apply these methods using supervised and unsupervised learning techniques in medical science. However, until present, nobody has attempted to encode SVs in genomes larger than one base, here we call DIPs. As an example, deep learning has been deployed to predict gene expression from histone modifications [8]. A genome-wide assay of breast cancer by Denoising Autoencoders (DAs) employs a data-defined learning objective independent of known biology [9]. So by using this independent system the information is not captured for any advantage. Covolution neural network has been used for classifying various kinds of tumors [10]. Deep learning has been used for pathology image classification [11] and does not tap into the SV of the genome information for the purpose. Recurrent neural network without deploying SVs of the genome has been used for heart failure onset [12]. In Articles ‘The next era: deep learning’ and ‘Deep learning in drug discovery’[13,14] act as a review article for deep learning in pharmaceutical re-search and drug discovery-SVs of genome for any advantageous role are not mentioned. Brain disorders, such as Alzheimer’s disease, are evaluated using brain images using artificial intelligence techniques in article ‘Ensembles of deep learning’[15], yet heart related disorders use deep learning for mag-netic resonance information [16]. Article ‘Deep learning applications for’ [17] tries to make use of transcriptomics data along with deep learning for drug prediction and repositioning, again SVs of the genomic data are not mentioned. Recently in 2019, article ‘Machine learning SNP’[18], visits the idea of machine learning by SNP-only based approach, which fails to point out the impact of DIPs and its appropriate encoding to facilitate machine and deep learning.

SVs ‘Variations in Genome Architecture’[19] in genomic data are obtained after comparing the patient’s DNA sequence with a reference sequence and finding matches and mismatches using tools, such as GenomeBreak [20,21]. In-corporation of DIPs or InDels to MLCSB cannot be avoided, as we are generating more and more sequences and the data is routinely being downstream analyzed for SVs. As DIPs essentially have all in-formation for CNVs, inversions, translocations and other SVs on genome, encoding them would also indirectly encode the other SVs. Article ‘A105 Family Decoded: Discovery of Genome’ [22], discusses utilizing tools for these SV detections, then comparing these variations to databases and conducting a knowledge mining [23] where these variations are known to be associated with a disease. Clearly, there will be many times when these variations cannot be validated experimentally, and thus machine and deep learning models would need to be deployed to understand these molecular variations signatures, as well as to see their importance in being associated with a complex disease. DNA sequencing for individuals is becoming increasingly cheaper to obtain, for example via NGS at sequencing centers where it can be done at a scale thereby distributing the fixed cost [24]. Once these variations are obtained, we need to encode them logically for a representative justified number that can be downstream deployed to deep and machine learning algorithms to see if the training results converge in test data.

Methods

The method discussed in this paper is based on a small pilot dataset of less than 200 individual for demonstration purpose of DMWAS. There would be more power in the analysis once the dataset is scaled up to thousands of individuals. Article ‘Customized biomedical informatics’[25], showed qualitatively that the deviation of the sum of the nucleotides in DIPs was generally higher than the deviation of the sum of the nucleotides of the SNPs for the whole genome. In other words, deviations in DIPs were more representative of the individual differences among them and could thus attribute to their differences in endo-or-end phenotype. As an example, Article ‘Customized biomedical informatics’ [25] took the gender as the end phenotype and showed that the variance (and the standard deviation) between the set of structural variations (DIPs) was much higher than that of the sum of nucleotides of SNPs (Figure 1), and stating that structural variations were a stronger means to determine the phenotype, i.e. gender here. Inspired by the article, this paper is about fine tuning and quantifying individual DIPs, so we introduce a deviation from consensus score to quantify the differences in SVs for these letters while also using one-hot encoding for the single nucleotide bases.

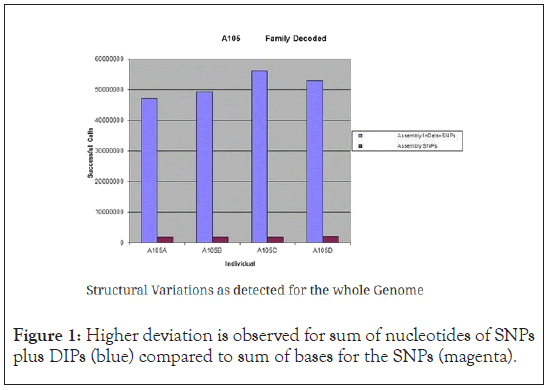
Figure 1: Higher deviation is observed for sum of nucleotides of SNPs plus DIPs (blue) compared to sum of bases for the SNPs (magenta).

We used DMWAS suite to simulate genomic data for genomic co- ordinates as a combination of A, T, GC or a 4-letter combination for a larger letter. Comprised of a Python script genSampleData. py, it can be used to generate genomic variation data specifying quantity of genomic loci, number of patients, frequency of occurrence of DIPs, and the maximum size of a DIP. Details of usage of script are specified in the downloadable ReadMe.md file from GitHub. For illustration purpose we are using 400 genomic co-ordinates. Typically, once the single letters are encoded to be present or not present at a certain genomic locus, they can be encoded as 1 or 0, longer letters are left as is. The letter ‘I’ is introduced to signify insertion wherever there are larger words of more than one letter and will take in value as 0 or the large word sequence based on absence or presence of inserted word respectively.

In Figure 2 are the simulated data for 40 columns and 8 patients. The simulated genotype data for 200 loci is provided as file multi- ColumnSample.csv. Once the simulated data is generated, and then we use the script splitMultiColDIPs.py to split each feature column into two columns, one column for 1 letter variants and another column for DIPs variants. The split file is available by name multiCol-umnSplitSample.csv as shown in Figure 3 is an example of data with each column doubled as per described method.

Figure 2: Randomly generated Genotype data for 8 patients for illustration purpose. The example data chosen for simulation comprises of 40 individuals and 200 genotypic loci.

Figure 3: For illustration purpose, we show how the DIPs columns are generated, by splitting each feature column variable into 2.

With information for the DIPs as second column, we can extract them separately and conduct a clustering of the data such as by multiple sequence alignment, getting the divergence score for each DIPs from the consensus. While we could have worked on writing our own version of clustering algorithm, we decided to keep that as task for future while deploying existing tools that does clustering for the purpose of this paper. This method of encoding the letters based on divergence from a mean, median or consensus score is called ‘DivScoreEncoding’. DivScoreEncoding is different than one-hot, word embedding, index based encoding and other kind of label encoding methods as described in the article ‘Text Encoding: A Re-view’ [26].We realize that the InDels or DIPs can be different from each other and the difference in biological relevance such as by means of frame shift of codon or mutation at a point need to be given a score in biological context. The traditional means of encoding texts, such as those discussed at [26], do not take biological evolutionary distance into account when encoding for DIPs or In-Dels. These methods of DivScore Encoding are applicable to larger insertions and deletions as well as for other SVs in the genome like CNVs, translocations, etc. While critics might argue that insertions or deletions can simply be encoded as a new letter such as ‘I’, much of the variation from consensus information is lost in simplistic methods of encoding. Clustering methods are not new methods in this well-established domain. There is no reason why the benefits of such alignment for coding or non-coding region and score should not be used for downstream processing, such as in deep machine learning. Cross-species multiple sequence alignment has been tried using phylogenetic tree construction in article [27].In this paper we have distinguished ourselves by deploying multiple sequence alignment for feature scoring within a species, then using those features for downstream modeling to prioritize the dominant features in the model for the given trait. Articles ‘An integrative approach’ and ‘An integrative approach to’ [28,29] generate pathogenic scores of InDels throughout the non-coding genome to classify them into pathogenic or not, and would be clearly very different in terms of method and application, although the similarity remains in terms of the concept of giving a score to the InDels based on a biological role. Figure 4 shows a sample clustering by multiple alignments done words of varying length with consensus and divergence score for each sequence.

Figure 4: Example of a sample clustering by multiple sequence alignment with consensus regions and the consensus score with individual scores as well (which we call divergence score in this paper).

For implementing DivScoreEncoding method by clustering, we have chosen T_coffee [30] software application to get the divergence score. This third-party software is available online. A wrapper Python script multiColDIPsDiv.py is provided, which automates extraction of the DIPs from multiCoumnSplitSample.

csv file, then passes it to T_coffee software for multiple sequence alignment and divergence score determination. The idea is to get divergence scores from the consensus. Only T_coffee has been used to illustrate the idea, while other statistical techniques for divergence score determination can be explored and adopted for optimality. Script re-verseReadMulti.py is provided to reverse the scores obtained, and script ReplaceMultiColDIPsNew.py can be used to replace the DIPs with appropriate scores. This would lead to file with content such as in Figure 5.The resulting file is also provided as Multi-ColDIPsScored.txt. Before or after encoding the DIPS, once SNPs and DIPs columns are split, we can encode the SNPs. It will be best to encode the SNPs columns after the DIPs columns, using the scripts and flow above, and then encode the SNPs by one hot en-coding. The Python script encodeSNPs.py has been provided for this purpose; the resulting final scored and encoded file Multi-ColDIPsScoredEncoded.txt is also provided. Figure 6 shows a sample scored and encoded file snippet.

Figure 5: The DIPs are replaced by the corresponding divergence from consensus score, lying between 0 and 100.

Figure 6: Now, the single nucleotide variations, SNVs or SNPs, are also one-hot encoded.

Next step is to look for phenotype value. Using results for simulated data ensures the performance would be better than this in the real case data compared to this random data. Next phenotype values were generated- 1 for presence and 0 for absence of the phenotype. Since we had 40 individuals or rows, we generated 40 y-values 0-39, with the 1st row left as that of feature column variable names. File is named as Phenotype.txt. Now that the dependent column variable values and independent feature variable values have been prepared, we decided to use several machine learning methods, such as logistic regression, naïve bayes, gradient boosting, bagging, and adaboost, and deploy enhanced form of exhaustive multi-layer perceptron (MLP=in the form of DNN by incorporating early stopping criteria to avoid overfitting, using rectified linear unit (ReLU) as activation function to reduce weight adjustment time and addressing the vanishing gradient problem. We also introduce an exhaustive nature of exploration for the right hidden layer and hidden units by varying the number of layers and number of hidden units in the DNN in a loop. Each time the best scores were chosen for its number of hidden layers and units. This exhaustive nature of DNN, when the range was given in realistic bound proved more useful than simply adding hidden layers as in a typical DNN, and thereby gave profound results, so this approach is called ‘Exhaustive DNN’. The scripts ExhaustivDNN.ipynb and ExhaustiveDNN.py are provided in DMWAS and feeds in MultiColDIPsScoredEncoded.txt as input file. The script internally looks for all columns with any null values that are removed before modeling. The data file was also separately checked for Null values and minor allele frequency (MAF) of at least 5% and the resulting encoded file is available at DMWAS as NullMafMultiColDIPsScoredEncoded.txt, which can be used as an alternative. From this file applying F-Test criteria for each of the feature columns we chose the top 1% of the feature set as the final data that the deep and machine learning scripts would work on. Once the models are generated by the various deep and machine learning scripts, we can then look for partial dependence score for each feature column and thereby have a final feature set optimization i.e., in our data the set of genomic variants. Feature set optimization has been an active area of research recently such as what we see in article ‘Feature set optimization’ [31]. Article ‘Opportunities and obstacles’[32] talks about various applications of deep learning in different spheres of biology and to which Exhaustive DNN as part of DMWAS with the DivScore Encoding methodology can play vital role as it is exhibited in the results section later.

Results

Exhaustive DNN proved very useful. 30% of data was used for test and prediction purpose, results shown as a confusion matrix. In less than a minute it resulted in model that was 100% accurate on the test data with the following configuration of hidden layers and hidden units, and the score on average for each training batch as 96%:hidden units: 8, hidden layers: 2, avg_score:0.9600000023841858. The confusion matrix is shown in Figure 7. It should be noted that continuing to run Exhaustive DNN to get higher accuracy would take a lot of computational resources. Here accuracy is defined as: Accuracy=(TP+TN)/ (TP+FP+FN+TN)

Figure 7: Confusion MATRIX for ExhaustiveDNN model for simulated dataset.

Machine learning techniques, mentioned in previous section, were applied as well for which (Figure 8) shows their corresponding confusion matrices. Each script took less than 1 minute to produce the confusion matrix, precision-recall curve, roccurve and list the dominant features. The scripts are available in DMWAS as createLogi-tReg.py, createAdaBoost. py, createBagging.py, createGradi-entBoosting.py and createNaiveBayes.py, extratreeclassifier.ipynb, randomforest. ipynb, support vector.ipynb. Given the current work context, we only discuss the confusion matrix produced by these software implementations of the various machine learning algo-rithms, which is enough to determine accuracy. When there would be imbalance in distribution of cases and control, then PR-Curve metrics would be worthwhile to discuss, as we later plan to scale up the work for larger dataset analysis in future. All results for ROC-curve, PR-Curve, list of dominant column variables, etc. are made available at DMWAS GitHub. Table 1 below summarizes the accuracy values obtained from these machine and deep learning software tools.

Table 1: ExhaustiveDNN outperforming some of the popular Machine Learning methods for simulated dataset.

Figure 8: Top left to bottom right: Confusion MATRIX for logistic regression, Naïve Bayes, Gradient Boost, Bagging approach, AdaBoost, RandomForest, Support Vector and Extratree Classifier respectively for simulated dataset.

Using these approaches, the Naïve Bayes method seems to have the highest positive hits detected with 75% accuracy in this simulated data.

However, using the Exhaustive DNN approach with a variation of number of layers and hidden units, with early stopping conditions, gave the best result with an accuracy of 100% almost immediately. The trick is to set the initial set of hidden layers and hidden units large enough while running Exhaustive DNN. However, Exhaustive DNN is smart enough to store the best model if you let the script execute for a given range. It uses k-fold test data splitting where k is taken as 10, for splitting the dataset, and then taking 1 split dataset at a time to test the accuracy keeping the rest for training. This is repeated for all 10 sets and the average score is reported. The initial opinion of 100% accuracy would be that the model has perhaps done over-fitting, the early stopping condition ensures that over-fitting does not take place. This is further substantiated by the fact that Exhaustive DNN does not give 100% accuracy in real GTEx data, as discussed later. The codes for Exhaustive DNN with early stopping condition have been shared as a separate python script at DMWAS GitHub page. Exhaustive DNN when allowed to continue after the 1st model has been generated can lead to multiple models, each with different average accuracy score such as that shown below in Table 2 at epoch (cycles) of 100. The model with best average score is saved for its configuration to be used on test and real data.

Table 2: Exhaustive DNN leading to several different average accuracy score for various combinations of hidden layers and hidden units.

Application of DMWAS to GTEx V7 Pilot dataset

We used the scripts of DMWAS for Genotype-Tissue Expression (GTEx) project V7 pilot dataset of 185 individuals, for the phenotype coded as MHHRTATT for the people who died of ‘heart attack, acute myocardial infarction, acute coronary syndrome’, and were able to see that most of the machine learning based algorithms could perform remarkably better for real case data. As an example, Figure 9 shows the AUC for ROC curve for logistic regression for the MHHRTATT phenotype. ROC curve plots for simulated data using various deep learning and machine learning tools are available at DMWAS GitHub page as additional resources. A score of 97.3% accuracy was obtained using logistic regression model of DMWAS as shown through the confusion matrix in Figure 10 for which the test data was taken as the entire GTEx V7 Pilot dataset. Then we deployed all the implementations of various algorithms that were previously tested for simulated data and took 30% of the GTEx V7 Pi-lot dataset size, 185 × 0.3=56 (round figure). The results obtained have been summarized in Table 3. The plots for various confusion matrices are shown as well in Figure 11.

Table 3: List of various machine and deep learning algorithms with the score of their accuracy.

Figure 9: ROC curve for Logistic regression in DMWAS suite MHHRTATT trait for GTEx V7 pilot dataset.

Figure 10: Confusion Matrix of Logistic Regression of DMWAS on GTEx V7 Pilot data for MHHRTATT trait giving accuracy of 97.3%.

Figure 11: Confusion Matrices top to bottom for Exhaustive DNN, Logistic Regression, AdaBoost, GradientBoost, Naïve Bayes, Bagging, Support Vector, Random Forest, ExtraTreesClassifier for MHHRTATT phenotype GTEx V7 Pilot dataset.

Discussion

UEvidently for the given dataset of GTEx V7 Pilot the methods of support vector and logistic regression substantially outperformed other methods in terms of accuracy. Although most methods could detect the unaffected diseased individuals, support vector and logistic regression correctly classified majority of the individuals affected by MHHRTATT trait. Since true positives in the dataset were significantly less, once scaled up from pilot dataset to whole dataset analysis, such as for GTEx V8 data, the method would help deter-mine the precision rather than just depend on accuracy. Nevertheless, substantially good results from logistic regression and support vector machine methods were obtained as reflected in the substantial number of true affected cases that were predicted to be truly affected.

The performance of the machine learning algorithm deployed would also depend greatly on how the encoding of genomic variations is done, such as the large words insertions. As the actual data size of human genome is about 6 billion for diploid genome per individual, more sophisticated methods for feature prioritization need to be deployed on a high-performance parallel computing hardware for realization of these methods, discussed in this article for practical implementation, if we are to not use the F-Test criteria to prioritize and reduce the data. For illustration purpose on real data, we showed how the results improve drastically as we achieve accuracy of 97.3% for real case data of GTEx V7 Pilot, for logistic regression, compared to only 58.3% as in randomly generated simulated dataset. This 97.3% of accuracy was generated when the entire GTEx V7 Pilot data was used for testing purpose.

This paper was to present ideas and implement innovative methods for small simulated data to aid in the future of healthcare, medicine and bioinformatics in general. The tools and techniques dis-cussed in DMWAS can be applied for solving other data science problems as once the encoding work is completed, the user can use any algorithm of his choice and not be locked into using those provided or suggested in this paper. This applies to the clustering DivScore Encoding method as well. For instance, we can give each letter a value, then calculate a mean or median score for the complete word, or use other sophisticated clustering method which use fuzzy logic for instance. The author has only tried to present the idea by an implementation and has not tried to optimize as to what score could possibly be best suited. Optimizing and finding the best algorithm to determine best score of DivScore Encoding for machine learning purpose can be scope of future work. Implementing DMWAS on a real genomic set of data for projects that sequence not just the SNPs but also InDels of patients would be our priority for future work.

Optimized feature set for MHHRTATT biomarkers

These models can help us ‘optimize the feature set’ i.e., identify dominant variants that are strongly associated to the model - and thus to the disease. The possibility was explored on the simulated dataset as well as prediction was made for MHHRTATT trait for the GTEx V7 pilot dataset to see if we get a score for the DIPs variant columns. Table 4 lists a partial dependence score generated for the simulated data in which the variant columns were also captured. The partial dependence score is calculated for genomic variant columns having single nucleotide variant eg. 214_C would mean the C nucleotide at 214th column in the genome variant file, for showing that just the presence of DIP at a position eg. 232_I means that the 232nd genomic variant column having an insertion, for showing the effect of the insertion variants at that column simply the column number is stated eg. 377. Clearly, scores were the highest for those genomic columns for which the encoding was done for their insertion using the methods described in this paper. For the real case da-ta the top 10 optimized features were all belonging to InDel class as shown in Table 5 for the logistic regression; the column variable name and numbering is as per the GTEx data with extension file-name.PED and the actual co-ordinates can be found by looking at the corresponding rows of .MAP file. Note that since the.PED file comprise of one major allele and another minor allele information, the number of columns with regard to the genotype information is twice that of the number of rows in .MAP file and so tracing back of the corresponding genomic map coordinate should be done accordingly. As an example if the optimized feature has name 16,830,168_G, then the .PED file corresponding feature co-ordinate removing the initial 6 columns is 16,830,168 and the genomic variant that is having an effect is G. The corresponding genomic map coordinate line number is CEILING (16,830,168/4)=4,207,542. We divide by 4 since the GTEx data is generated for each allele for heterozygosity. This in the .MAP file corresponds to variant Id kgp30994055 and at position 52587347 of chromosome 23. The list of top associated and least associated genomic variants with their chromosome number, variant Id, and genomic loci are stated in Tables 5 and 6 respectively. Apparently, the lowest scoring features were all SNPs (Table 6) however, the relative difference in the tops scorer and bottom scorer were not huge indicating a rheostat model of combined effect of the variants on the phenotype. However, there might be other traits as we shall evaluate as part of our future work, where we might see a huge difference in partial de- pendency score.

Table 4: List of partial score and the corresponding column explanatory genomic variant variable.

Table 5: List of top 10 partial score as per the logistic regression and the corresponding column explanatory genomic variant variable column number as per the GTEx V7 pilot data numbering. The corresponding genomic co ordinates can be found using the .MAP and PED file information from GTEx dataset as described in ‘Optimized Feature set for MHHRTATT biomarkers’ section and are also shown in the table.

Table 6: List of bottom 10 partial score as per the logistic regression and the corresponding column explanatory genomic variant variable column number as per the GTEx V7 pilot data numbering. The corresponding genomic co-ordinates can be found using the .MAP and .PED file from GTEx dataset information as described in ‘Optimized Feature set for MHHRTATT biomarkers’ section and are also shown in the table.

Conclusion and Future Work

This paper has demonstrated and advocates use of clustering divergence score as a new way of genomic variant encoding particularly for structural variants larger than point mutations and demonstrated in for InDels, though the technique can well be applied to other SVs such as copy number variants, etc. We then deployed certain deep learning and machine learning methods for which we have provided the code as DMWAS at GitHub with sample results and script to simulate data. Several machine learning algorithms were experimented and MLP (multi-layer perceptron) script with alterations to gain properties of deep learning was developed in Python, such as early stopping condition to avoid over-fitting. This led us to 100% accuracy using Exhaustive DNN for the simulated data while accuracy for the real data was lower; confirming no case of over-fitting as far as the script logic is concerned. Other machine learning techniques such as bagging gave results lower than DNN with highest being 75% using Naïve Bayes for the simulated data. We conclude that results and performance depend on the data and algorithm used for machine learning including deep neural network. The concept of clustering score is central to the ideas discussed in this paper and once the divergence scores are obtained, the downstream model-ing advance algorithm need not be just restricted to those mentioned in DMWAS GitHub page but could also use many other deep and machine learning algorithms such as even genetic algorithm as has been used for GARBO.

We used DMWAS for actual data such as for GTEx V7 pilot and prioritized models that showed more than 90% accuracy and thereby demonstrated on simulated data as well that the genomic variant column variables can be assigned a partial dependency score. We gave results for optimized feature for the top 10 genomic variants for MHHRTATT heart disease related death. Many of the top scoring variants were those genomic loci having InDels. Future work for DMWAS would require extracting and prioritizing the top variants using various trait or phenotype, for other traits as we demonstrated for MHHRTATT. Future work requires up-scaling the analysis for the entire dataset such as GTEx V8 since the number of cases of individuals having the trait in pilot sample is very limited, thereby having considerable under performance for most of the deep and machine learning models. Future work also asks for exploring and comparing performance of other similar tools that deploy machine and deep learning for GWAS, such as CADD even though it was used in cross-species context, or GARBO which uses fuzzy logic and genetic algorithm, and see if there are complementary aspects that DMWAS can benefit from, in a future version of the tool. The purpose of the current work was to not just describe a method, but also list top genomic variants associated to MHHRTATT. The idea is also to make DMWAS available and deployable for the purpose of deep learning and machine learning application to GWAS.

Open-Source Development & Distribution

The PR-Curve, ROC-Curve, PD Values (partial dependency scores based on the model for the genomic variant columns) for the simulated data and python scripts including script to simulate data is publicly accessible here: https://github.com/abinarain/ DMWAS. Note that the scripts work fine for small dataset on a modest computing facility.

Acknowledgement

The author thanks all developers and teachers of Python programming language.

References

1. Manolio TA. Genomewide association studies and assessment of the risk of disease. N Engl J Med. 2010;363(2):166-76.
2. Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet. 2007;39(7):906-13.
3. Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81(3):559-75.
4. Galesloot TE, van Steen K, Kiemeney LA, Janss LL, Vermeulen SH. A comparison of multivariate genome-wide association methods. PloS One. 2014;9(4):e95923.
5. Visscher PM, Brown MA, McCarthy MI, Yang J. Five years of GWAS discovery. Am J Hum Genet. 2012;90(1):7-24.
6. Singh AN. DMWAS: Deep Machine learning omics Wide Association Study and Feature set optimization by clustering and univariate association for Biomarkers discovery as tested on GTEx pilot dataset for death due to heart-attack. bioRxiv. 2021 Jan 1.
7. McClellan J, King MC. Genetic heterogeneity in human disease. Cell. 2010;141(2):210-7.
8. Singh R, Lanchantin J, Robins G, Qi Y. DeepChrome: Deep-learning for predicting gene expression from histone modifications. Bioinformatics. 2016;32(17):i639-48.
9. Tan J, Ung M, Cheng C, Greene CS. Unsupervised feature construction and knowledge extraction from genome-wide assays of breast cancer with denoising autoencoders. Pac Symp Biocomput.2014 (pp. 132-143).
10. Huynh BQ, Li H, Giger ML. Digital mammographic tumor classification using transfer learning from deep convolutional neural networks. J Med Imaging. 2016;3(3):034501.
11. Janowczyk A, Madabhushi A. Deep learning for digital pathology image analysis: A comprehensive tutorial with selected use cases. J Pathol Inform. 2016;7.
12. Choi E, Schuetz A, Stewart WF, Sun J. Using recurrent neural network models for early detection of heart failure onset. J Am Med Inform Assoc. 2017;24(2):361-70.
13. Ekins S. The next era: deep learning in pharmaceutical research. Pharm Res. 2016;33(11):2594-603.
14. Gawehn E, Hiss JA, Schneider G. Deep learning in drug discovery. Mol Inf. 2016;35(1):3-14.
15. Ortiz A, Munilla J, Gorriz JM, Ramirez J. Ensembles of deep learning architectures for the early diagnosis of the Alzheimer’s disease. Int J Neural Syst. 2016;26(07):1650025.
16. Ngo TA, Lu Z, Carneiro G. Combining deep learning and level set for the automated segmentation of the left ventricle of the heart from cardiac cine magnetic resonance. Med Image Anal. 2017;35:159-71.
17. Aliper A, Plis S, Artemov A, Ulloa A, Mamoshina P, Zhavoronkov A. Deep learning applications for predicting pharmacological properties of drugs and drug repurposing using transcriptomic data. Mol Pharm. 2016;13(7):2524-30.
18. Ho DS, Schierding W, Wake M, Saffery R, O’Sullivan J. Machine learning SNP based prediction for precision medicine. Front Genet. 2019;10:267.
19. Singh AN. Variations in Genome Architecture, Poster. In International Congress on Personalized Medicine. pp. 2-5.    
20. Singh AN. Comparison of Structural Variation between build 36 Reference Genome and Celera R27c Genome using GenomeBreak, Poster Presentation. In The 2nd Symposium on Systems Genetics, Groningen 2011 Sep (pp. 29-30).  
21. Singh A. Genome-Break: A versatile computational tool for genome-wide rapid investigation, exploring the human genome, a step towards personalized genomic medicine.
22. Singh AN. A105 Family Decoded: Discovery of Genome-Wide Fingerprints for Personalized Genomic Medicine. In Proceedings of the International Congress on Personalized Medicine UPCP 2012 (pp. 115-126).  
23. Singh AN. Knowledge Mining and Bioinformatics Tools to Advance Personalized Diagnostics and Therapeutics. InUSISTF organized Workshop, Florence Nov 2012. 
24. Schwarze K, Buchanan J, Fermont JM, Dreau H, Tilley MW, Taylor JM, et al. The complete costs of genome sequencing: a microcosting study in cancer and rare diseases from a single center in the United Kingdom. Genet Med. 2020;22(1):85-94.
25. Singh AN. Customized biomedical informatics. Big Data Anal. 2018;3(1):1-2.
26. Data Science Central.Text Encoding: A Review Posted by Rosaria Silipo on February 11, 2019 at 3:09pm.
27. Rentzsch P, Witten D, Cooper GM, Shendure J, Kircher M. CADD: Predicting the deleteriousness of variants throughout the human genome. Nucleic Acids Res. 2019;47(D1):D886-94.
28. Ferlaino M, Rogers MF, Shihab HA, Mort M, Cooper DN, Gaunt TR, et al. An integrative approach to predicting the functional effects of small indels in non-coding regions of the human genome. BMC Bioinformatics. 2017;18(1):1-8.
29. Shihab HA, Rogers MF, Gough J, Mort M, Cooper DN, Day IN, et al. An integrative approach to predicting the functional effects of non-coding and coding sequence variation. Bioinformatics. 2015;31(10):1536-43.
30. Notredame C, Higgins DG, Heringa J. T-Coffee: A novel method for fast and accurate multiple sequence alignment. J Mol Biol. 2000;302(1):205-17.
31. Fortino V, Scala G, Greco D. Feature set optimization in biomarker discovery from genome-scale data. Bioinformatics. 2020;36(11):3393-400.
32. Ching T, Himmelstein DS, Beaulieu-Jones BK, Kalinin AA, Do BT, Way GP, et al. Opportunities and obstacles for deep learning in biology and medicine. J R Soc Interface. 2018;15(141):20170387.