Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2014) Volume 3, Issue 2
After finding a poor relation between average return and beta’s of the 25 largest firms traded in the NASDAQ, we modified the classical CAPM model in order to improve the predictive power of the model. Our first approach is that the capital market line should pass through the market portfolio while risk free interest rate would be estimated by a linear regression that minimizes the square distance of various stock data from the line. The second approach is that the traditional market line is valid, but the formula for calculating beta should be modified. Under the first approach, we find a very large interval for expected return while under the second we find unreasonable values for beta. According to our findings, we conclude that factors other than beta should be used for determining risk.
<Keywords: Average return, Beta?s, CAPM, NASDAQ
While the beta measure and CAPM are considered to be the cornerstones of financial theory, researchers continue to challenge the abilities of these models from all angles. Replications of the model with more recent data have failed, nearly every time, to explain returns.
Empirical research on the association between average returns on beta includes studies by Jensen et al. [1], Blume and Friend [2] and Fama and MacBeth [3]. Fama and French [4] found that three factorsthe market portfolio and the differences in portfolios as indices; the difference in returns on portfolios of small stocks and large stocks, and the difference in returns on portfolios containing stocks with high book to market ratios and stocks with low book to market ratios - can explain the cross-section of returns.
Fama and French [5] feel that yield surrogates, such as dividend and earnings yield, are correlated with returns because they proxy for underlying risks not accounted for by beta. As for the possible reasons for size effect, Roll [6] suggested this may be due to errors in risk management, in particular less frequent trading of small firms.
Merton [7] developed a model of capital market equilibrium with incomplete information, CAPMI, to provide some insights into the behavior of security prices. He also studied the equilibrium structure of asset prices and its connection with empirical anomalies in financial markets.
Fama and French [8] describe a divergence of opinion among researchers for the imperfect empirical record of the CAPM. While Fama and French [8] discourage use of the CAPM for empirical work, 80 percent of corporations and financial advisers surveyed by Bruner [9] nevertheless use the CAPM to estimate the cost of equity capital.
If we assume that the CAPM theory has high predictable power, we can think of two possible reasons for its lack of ability to empirically forecast a good fit between stocks’ beta and stocks’ return. The first is that the risk-free interest rate is not correct so that the market line is not depicted correctly, while the second is that the classical formula for calculating stocks’ undiversified risk is wrong. In this paper, we revised and adjusted the classical approach in order to compete with the bad performance of the CAPM.
We used the daily return data of the 25 largest companies traded in the NASDAQ, for the period January 2nd, 2008 – April 21st, 2010.
Assuming that the NASDAQ index represents Market Portfolio, we calculated the systematic risk of each stock as ρσj, where ρ is the correlation coefficient of the stock and the NASDAQ index, while σj is the standard deviation of the stock. Dividing systematic risk by the standard deviation of the NASDAQ index we get:
 (1)
(1)
where σm is the standard deviation of the NASDAQ index.
Table 1 presents the expected return of each stock and its Beta sorted according to Beta in descending order:
| Average yearly Return (250 days) | Average Daily Return | Beta | |
|---|---|---|---|
| Citigroup | -12.59% | -0.05% | 2.047917 |
| Bank of America | 20.15% | 0.08% | 2.022756 |
| Wells Fargo & Company (WFC) | 43.71% | 0.17% | 1.713418 |
| JPMorgan Chase & Co. (JPM) | 32.68% | 0.13% | 1.661409 |
| General Electric | -14.49% | -0.06% | 1.092923 |
| Intel | 6.64% | 0.03% | 1.086299 |
| Cisco Systems | 9.14% | 0.04% | 1.066738 |
| Apple | 22.78% | 0.09% | 1.02714 |
| NASDAQ Composite (^IXIC) | 3.75% | 0.02% | 1 |
| Microsoft | 3.18% | 0.01% | 0.979034 |
| Oracle | 14.35% | 0.06% | 0.960841 |
| Chevron | 2.89% | 0.01% | 0.95868 |
| -0.22% | 0.00% | 0.951502 | |
| Hewlett Packard | 10.72% | 0.04% | 0.864505 |
| Exxon | -5.91% | -0.02% | 0.84742 |
| AT&T | -12.95% | -0.05% | 0.793351 |
| Merck | -13.19% | -0.05% | 0.72006 |
| IBM | 13.62% | 0.05% | 0.714722 |
| Pfizer | -8.30% | -0.03% | 0.676823 |
| Berkshire Hathaway | -44.67% | -0.18% | 0.619773 |
| Philip Morris International | 7.84% | 0.03% | 0.589618 |
| Procter & Gamble | -2.09% | -0.01% | 0.529031 |
| Coca-Cola | -1.22% | 0.00% | 0.515437 |
| PepsiCo | -2.26% | -0.01% | 0.494163 |
| Wal-Mart Stores Inc. (WMT) | 10.06% | 0.04% | 0.480176 |
| Johnson & Johnson | 2.28% | 0.01% | 0.467022 |
*) see in Appendix 1 correlation coefficient and systematic risk
Table 1: Average Return and Beta (*).
As we can see in Figure 1, higher beta does not necessarily guarantee a higher return.
In the “Capital Asset Pricing Model”, the Capital Market Line is a straight line that connects the Market Portfolio and the risk-free rate of interest.
The beta for each stock is defined as its systematic risk divided by market risk (Figure 2).
Comparing Figures 1 and 2, we can see that stocks do not lie along a straight line (the correlation coefficient between stocks’ betas and returns is 0.41).
Wrong capital market line
If the risk-free interest rate is wrong and the stock risk indicator is wrong, the capital market line does not represent a good fit between stocks’ risk and return.
Figure 3 demonstrates two market lines, where each line is depicted for a different level of risk-free interest rate. Assuming that the market portfolio is true, the line slope changes when the risk-free interest rate is changed. In addition, if the stocks’ risk indicator is wrong, the line does not represent the true expected return of the stock.
In order to demonstrate this, let us assume that classical “systematic risk” does not contain all aspects of risk and that β'j in equation 1 defines the real stock risk.
 (2)
(2)
εj might be affected by various random factors that are idiosyncratic to stock j, a disturbance that cannot be distributed by diversification and is idiosyncratic to a current period (historical data, such as standard deviation, do not contain information in regard to εj).
As we can see, the result of wrong assumptions regarding the level of a risk-free interest rate as well as the risk indicator of a stock is a poor relation between risk and return.
We will try two approaches in order to combine theory and field:
• We will not depict the Capital Market Line in advance as a line connecting risk-free interest and market portfolio. Instead, we should depict a line that passes through the market portfolio; however its slope (and the intersection point with the vertical axis) should be determined by estimating a regression line that brings the distance of stock data from the line to a minimum. Such a line might be a better indication to the actual relation between stocks’ beta and the expected return. Using the estimated line, we will be able to calculate the confidence interval of forecasted stock returns.
• Although under a classical definition systematic risk, ρσj, (undiversified risk) represents stocks’ risk level, we saw above that empirical facts do not support the connection between classical beta and return. Instead of using the classical definition of systematic risk for calculating stocks’ beta, we will assume that the Capital Market Line is optimal and identify stocks’ beta as the horizontal distance of the line and the vertical axes (We should notice that now the beta of each stock j is not necessarily equal to its classical definition: 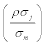
Capital market line according to possibility 1
Let assume first that the market systematic risk is well defined and is well connected in reality to stock returns. It means that εj = 0 ∨j .
Deviations might occur only due to the use of wrong risk free interest rate.
In order to avoid the use of wrong risk free interest rate, we can estimate the risk free interest rate while assuming that all other components are correct, by estimating equation (3) and assuming that the line passes through the market portfolio.
μj = α + γβj + εj (3)
Equation (3) determines the capital market line that connects stock returns and their systematic risk as defined by β. Where α and γ are parameters while μj and βj are stock j’s expected return and beta respectively (j =,1,2,….k, where k is the number of traded stocks).
The Capital Market line is not depicted as a line that connects market portfolio and the risk-free rate of interest, but rather as a line that passes through the market portfolio while defining the intercept by minimizing the square distance of the points that represents various stocks from the line, as presented in Figure 4.
We should estimate line parameters by solving:
 (4)
(4)
Where μm is the market portfolio expected return and βm is its beta.
Since βm = 1 (Point M represents market portfolio), we should solve:
 (4')
(4')
Differentiating we get:
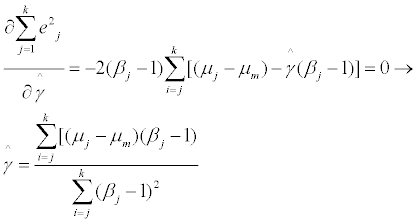 (4")
(4")
Estimating confidence interval for stock return
Using the estimated capital line, given stocks’ beta, we can forecast for each stock a confidence interval for its expected return.
Given that our estimated equation is:
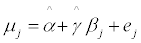 (5)
(5)
The standard error of the regression is:
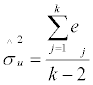
While the forecast standard deviation of observation q is:
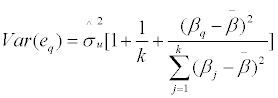 (6)
(6)
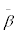 is average stocks’ β.
is average stocks’ β.
We get that the confidence interval of forecasted expected return of stock q is:
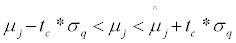 (6a)
(6a)
Where tc - is critical t value for a given significant level and 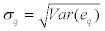
We should notice that according to the proposed model, the expected return cannot be determined at a definite level. We can determine it at a given interval with a certain confidence (probability).
Estimation of expected return
Using the data presented in Table 1, we estimated the model:
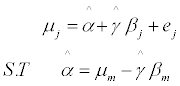
or

to get the estimation results (Table 2).
| 0.1683826 | R Square | |||
| 0.1283826 | Adjusted R Square | |||
| P-value | t Stat | Standard Error | Coefficients | |
| 0.03316 | 2.254702 | 0.069253 | 0.1561454 |  |
Table 2: Estimation Results.
The estimated equation is:
μj – μm = 0.15614*(βj – 1) + ej (7)
We calculated the forecast confidence interval of the expected return as defined by equation (6a) above (Appendix 2 and Figure 5).
As we can see, at a 95% confidence level, the intervals of returns are very large and in all cases we cannot determine an interval that is entirely in a positive or entirely in the negative range.
Capital Market Line and calculated betas according to possibility 2
In Figure 6 σj defines stock’s j standard deviation while k represents a possible portfolio created as a combination of the market portfolio and a risk free interest rate.
We can see that:
σj = A + B = σK + B (8)
However, as we saw in Table 1 above σK and  the classical risk measure, have a very poor connection to stocks’ return.
the classical risk measure, have a very poor connection to stocks’ return.
The question we ask ourselves is “what is the beta implied by the market stock return?”
Assuming that CAPM gives a perfect fit between risk and return, we will derive stocks’ beta as implied by the capital market line.
Using the market line equation we get that:
 (9)
(9)
and:
 (10)
(10)
Using equation (10) and assuming that the risk free interest rate is i = 1%1, we calculated beta for 25 NASDAQ stocks (Table 3).
| Beta | Average yearly Return (250 days) | |
|---|---|---|
| Wells Fargo & Company (WFC) | 15.51144 | 43.71% |
| JPMorgan Chase & Co. (JPM) | 11.50547 | 32.68% |
| Apple | 7.908602 | 22.78% |
| Bank of America | 6.954037 | 20.15% |
| Oracle | 4.847086 | 14.35% |
| IBM | 4.584529 | 13.62% |
| Hewlett Packard | 3.530219 | 10.72% |
| Wal-Mart Stores Inc. (WMT) | 3.289944 | 10.06% |
| Cisco Systems | 2.955432 | 9.14% |
| Philip Morris International | 2.482955 | 7.84% |
| Intel | 2.049907 | 6.64% |
| NASDAQ Composite (^IXIC) | 1 | 3.75% |
| Microsoft | 0.793325 | 3.18% |
| Chevron | 0.685488 | 2.89% |
| Johnson & Johnson | 0.463335 | 2.28% |
| -0.44351 | -0.22% | |
| Coca-Cola | -0.80769 | -1.22% |
| Procter & Gamble | -1.12371 | -2.09% |
| PepsiCo | -1.18412 | -2.26% |
| Exxon | -2.50999 | -5.91% |
| Pfizer | -3.37671 | -8.30% |
| Citigroup | -4.937 | -12.59% |
| AT&T | -5.06563 | -12.95% |
| Merck | -5.15229 | -13.19% |
| General Electric | -5.62613 | -14.49% |
| Berkshire Hathaway | -16.5866 | -44.67% |
Table 3: Beta and Average Yearly Return for 25 NASDAQ stocks.
It is not surprising that now the relation between stock return and recalculated beta is linear. However, betas, in absolute value, seem to be much larger than expected.
In this paper, we examined the relation between the NASDAQ 25 largest firms’ beta and expected return. We find a relatively low correlation between beta and return, with a correlation coefficient of 0.41. We examined two possible modifications of the CAPM model in order to try improving the poor relation between risk and return. The first is that the classical capital market line does not represent the optimal investment line. According to this possibility, we estimated the best capital market line as a line that passes through the market portfolio, however its slope is calculated by estimating a regression line that brings to a minimum the distance of 25 stocks’ data from the line. Using the estimated line, we forecasted a confidence interval of the expected return for the 25 stocks. The calculated 95% confidence interval is very large for all stocks, a result that points to large uncertainty in regard to the expected return given the stocks’ beta.
The second is that the classical market line, which is depicted as the line that connects the market portfolio and risk-free interest rate does represent the optimal market line.
However, since according to our empirical findings the systematic risk calculated by the traditional formula, ρσj, does not represent systematic risk in reality, we calculated the beta of each stock, given its expected return, as the distance of the capital market line from the vertical axes. This beta does not resemble the beta calculated by the classical definition of systematic risk. Calculating the stocks’ beta according to this approach, they are found to be very large in absolute value and might indicate that we should reconsider whether they are the right factors for defining stock risk.
Since the betas that are calculated by the traditional formula seem not to represent a proper connection to expected return while betas that are calculated by using the market line seem to be unreasonable large in absolute value, we can conclude that factors other than beta should be used for determining risk.