The study of nanostructured materials exhibiting novel properties is one of the most fascinating fields of current research. Small nanomaterials are of particular-interest because of intriguing characteristics [1-4]. Nanoparticles with smaller dimensions may exhibit different properties in comparison with bulk material. The nanoparticles possess unique physico-chemical, optical and biological properties which can be manipulated suitably for desired applications [5]. Particular, gold chemistry plays a very important role in nanoelectronics and bionano-sciences [6].

Nanotechnology and nano-sensors are broad, interdisciplinary areas that encompass (bio)chemistry, physics, biology, materials science, electrical engineering and more. Nanomaterials are at the leading edge of the rapidly developing field of nanotechnology. Their unique size-dependent properties make these materials superior and indispensable in many areas of human activity. Gold nanoparticles are one of the most potentially useful nanoparticles. This is especially true in cancer therapeutics because of their photothermal properties. Gold nanoparticles are readily synthesised structures that absorb light strongly to generate thermal energy which induces photothermal destruction of malignant tissue [7-9].

Noble metals and their compounds have a long and distinguished history as therapeutic agents in medicine. Recent years have seen tremendous progress in the design and study of nanomaterials geared towards biological and biomedical applications. Particularly gold nanoparticles have attracted intensive interest, because they are easily prepared, have low toxicity and can be readily attached to molecules of biological interest. The gold nanoparticles have become more precious than pretty gold because of their wide use and applications [10].

The use of gold compounds in medicine, and many experts still consider gold to be among the most effective drugs for reducing inflammation in joints, thus reducing the symptoms of pain and stiffness. Several forms of gold are available, but usually one of the injectable forms of gold salt (e.g., gold sodium thiomalate [Myochrysine] or aurothioglucose [Solganal] is used. An oral tablet containing gold, called auranofin (Radaura), is also available. As diseases evolve, so too does the need for this robust and versatile metal to aid in the treatment of a range of conditions, now and into the future. That is why gold nanoparticles are medically more precious than pretty gold [10].

The Boson peak is usually studied in glasses [11-13], where enhancement of heat capacity is induced by disorder. The modelling of clusters may be important for understanding the mechanism which lead to this effect. In glasses, there are different local configurations of atoms that may be simulated by isolated clusters. In particular, it was found that the vibrational density of states (VDOS) exhibit an excessively low-frequency contribution [14,15]. A corresponding lowtemperature peak is observed in the temperature dependence of the specific heat if plotted as Cvib(T)/T₃.

Zhang and Douglas [16,17] usually study the Boson peak from the velocity autocorrelation function, but they are both concerned about an “excess” contribution to the vibrational density of states. This feature has been observed in metal nanoparticles and zeolites (see: Greaves) and attributed to the coordinated harmonic motions of groups of atoms in the boundary region of the particle. There are similarities here to a glass because the surface of a nanoparticle has many features in common with this class of materials. In cases where the modes have been resolved, the Boson peak has corresponded to a ring of oscillating particles, the relatively low mass being related to the relatively high mass of these modes. Farrusseng and Tuel [18] also studied the perspectives on zeoliteen capsulated metal nanoparticles and their applications in catalysis.

In the present work, only an in-depth study on the behavior of the Boson peaks which are linked to the vibrational spectrum [19,20], which are existed in small neutral gold clusters at low-temperatures.

Theoretical and Computational Procedure

The DFTB [21-23] is based on the density functional theory of Hohenberg and Kohn in the formulation of Kohn and Sham. In addition, the Kohn-Sham orbitals ψi(r) of the system of interest are expanded in terms of atom-centered basis functions {Φ_m(r)},

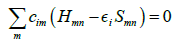(1)

While so far, the variational parameters have been the real-space grid representations of the pseudo wave functions, it will now be the set of coefficients cim. Index m describes the atom, where Φ_m is centered and it is angular as well as radially dependant. The Φ_m is determined by self-consistent DFT calculations on isolated atoms using large Slatertype basis sets.

In calculating the orbital energies, we need the Hamilton matrix elements and the overlap matrix elements. The above formula gives the secular equations:

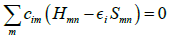(2)

Here, cim’s are expansion coefficients, ε_i is for the single-particle energies (or where ε_i are the Kohn-Sham eigenvalues of the neutral), and the matrix elements of Hamiltonian H_mn and the overlap matrix elements Smn are defined as:

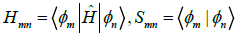(3)

They depend on the atomic positions and on a well-guessed density ρ(r). By solving the Kohn-Sham equations in an effective one particle potential, the Hamiltonian Ĥ is defined as:

(4)

To calculate the Hamiltonian matrix, the effective potential V_eff has to be approximated. Here,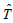being the kinetic-energy operator 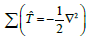and V_eff (r) being the effective Kohn-Sham potential, which is approximated as a simple superposition of the potentials of the neutral atoms,

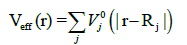(5)

V_j⁰ is the Kohn-Sham potential of a neutral atom, r_j=r-R_j is an atomic position, and Rj being the coordinates of the j-th atom.

The short-range interactions can be approximated by simple pair potentials, and the total energy of the compound of interest relative to that of the isolated atoms is then written as:

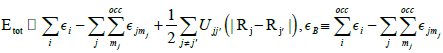(6)

Here, the majority of the binding energy (ε_B) is contained in the difference between the single-particle energies ε_i of the system of interest and the singleparticle energies ε_jmj of the isolated atoms (atom index j, orbital index mj),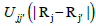 is determined as the difference betweenε_B and ε_B^scf for diatomic molecules (with ε_B^scf being the total energy from parameter-free density functional calculations). In the present study, only the 5d and 6s electrons of the gold atoms are explicitly included, whereas the rest are treated within a frozen-core approximation [21,23,24].

Calculation of vibrational heat capacity

Finally, from the calculated vibrational frequencies and with the use of Boltzmann statistics [25-27], we can get the formula to investigate size, structure and temperature effects on the vibrational heat capacity of clusters,

(7)

Here, N is the total number of atoms in a cluster, ħ is the reduced Planck’s constant, ω_i is vibrational frequencies (low(min), high(max)), k_B is Boltzmann’s constant and T is the absolute temperature. In this study, we focus only on the vibrational part of the heat capacity, i.e., on C_vib and the Boson Peaks, C_vib(T)/T³.

In this article, we present only an in-depth study on the behavior of the Boson peaks are thermally activated as well as the local atomic arrangements (within a cluster or group of strongly correlated atoms) but still are constrained by surrounding atoms [28]. This is an interesting point and may shed light on the enhancement of the heat conductance process mentioned in Ref. [29] and Ref. [30].

The Boson Peaks (BP) C_vib/T³ vs. T of the neutral gold clusters

As shown in Figures 1-3, with respect to the eqn. (7) and the corresponding Boson peaks C_vib/T³ vs. T were plotted at temperature within the range T=0.5-30 K.

Figure 1: Cluster Au₃: The C_vib per atom as a function of temperature at 0.5300 K. αi=ωi/T [violet line] and αi=ωi/(0.6950356 × T) of eqn. (7) [green line (Aquamarine 4)] and the corresponding Boson peaks C_vib/T₃ vs. T.

Figure 2: Au_5,6,9,12: C_vib per atom as a function of temperature at 0.5-300 K. αi=ωi/ (0.6950356 × T) of eqn. (7) and the corresponding Boson peaks C_vib/T³ vs T.

Figure 3: Au_N (N=3, 4, 10, 13, 14, 15, 18, 20): C_vib per atom as a function of temperature at 0.5-300 K. α_i=ω_i/(0.6950356 × T) of eqn. (7) and the corresponding Boson peaks C_vib/T³ vs T.

Au₃(C_2v): Figure 1 shows that the increase in Boson peak curve C_vib/ T₃ from 00.00035 k_B/atom [violet line] for αi=ωi/T and 0-0.001 k_B/atom [green line (Aquamarine 4)] for α_i=ω_i/(0.6950356*T) found for T → 0 → high temperature, 30K, and the maximum deviation at 6.00 K and 4.9 K, respectively, are due to a strong disorderly nature in the cluster. In addition to that confirmed with the parameter dependency.

Au₅(C_2v), Au₆(D_3h), Au₉(C_s) and Au₁₂(C₁): Figure 2 shows that the calculated C_vib/T³ vs. T for AuN (N=5, 6, 9, 12) in the temperature 0.5-10 K range. The increase in Boson peak C_vib/T³ from 0.88503 k_B/ atom (the maximum deviation with a higher amplitude at 0.6 K, Au5. Nevertheless, with the lesser amplitude the deviation occurs at 0.6 at 0.6 K for the other clusters, Au6, Au9 and Au12) found for T −→ 0 to higher temperature, the rest of the clusters are in the interval between 0.5 to 4 K.

Howsoever, Figure 3 also shows the calculated C_vib/T³ vs. T for Au_N (N=10, 14, 18, 20) in the temperature 0.5-30 K range. The detailed confirmation is given below.

Au₁₀(S₈): There is strong evidence that the maximum deviation of the Boson peak C_vib/T³ is 6.88469 × 10⁻⁵ k_B/atom at 12 K, is lesser amplitude than the all other clusters, which is only because of their large number of high frequency modes.

Au₁₄(C_s): Based on the experimental observations, the maximum in silica glass is placed at about 10 K and 8.5 K for neutral gold cluster (see Figure 3 and Richet et al. [31,32]), and the maximum deviation C_vib/T³ attains 2.4 × 10⁻⁴ J/(molK) for silica glass and 0.0004 k_B/atom for gold cluster, respectively. Please notice that the units are not the same.

Au₁₈(D₁): The C_vib/T³ deviation is 0.00178 k_B/atom found for T −→ 3.7 K temperature. It shows the disorder nature of the cluster.

Au₂₀(C₁): The C_vib/T³ deviation with a higher amplitude and the intervals in between 5.31 × 10^-3-4.97 × 10^-3 k_B/atom at 1-1.5 K, which has a large number of high frequencies modes.

Most importantly, the Boson peaks, C_vib/T³ are getting saturated that is towards closer to zero values (0 k_B/atom) at about 10 to 30 K above ranges. The lower frequencies certainly make a larger contribution to heat capacity. Nevertheless, the Boson peaks are highly visible, i.e., and the strength of the peaks strongly depends on the atomic coordination number. There are several origins, most of them related to the thermal fluctuations. If the atomic coordination is low, a single negative force constant renders the atomic arrangement much closer to an unstable situation than in the highly coordinated case [28].

We have extracted vibrational frequencies at T=0 K, and investigated the vibrational heat capacities at a temperature range 0.5- 300 K, of the re-optimized gold Figure 3; Au_N (N=3, 4, 10, 13, 14, 15, 18, 20): C_vib per atom as a function of temperature at 0.5-300 K. α_i=ω_i/ (0.6950356*T) of eqn. (7) and the corresponding Boson peaks C_vib/T³ vs. T. atomic clusters (Au_N=3−20). Especially, the vibrational modes with lower frequencies are given a significant contribution to the heat capacity at low temperatures. The vibrational heat capacity is a strong function of cluster size and temperature, particularly in the low temperature regime which is clearly seen at the Boson peaks. Overall, the Boson peaks shows the disorder nature of the clusters within the atomic coordination, as a zig-zag arrangement.

Dedication

Dedicated to Professor Prasanta Kumar Panigrahi, IISER, Kolkata, on the occasion of his 60th birthday, and Professor Kwang S Kim, UNIST, on the occasion of his 67th birthday.

A part of this work was supported by the German Research Council (DFG) through project Sp 439/23-1. We gratefully acknowledge their very generous support.