Journal of Ergonomics
Open Access
ISSN: 2165-7556
ISSN: 2165-7556
Research Article - (2017) Volume 7, Issue 6
Suspension seats are widely used in construction machinery to control vibration transmission and reduce discomfort and health risks to drivers. This study was undertaken via laboratory measurements to investigate the dynamic characteristics and performance of a suspension seat of a motor grader prior to optimising ride comfort of the grader. The isolation efficiency of the suspension seat was assessed in accord with ISO 7096: 2000. The vibration transmission of the suspension seat in the vertical direction was examined with different seat configurations and loading conditions. The results showed that the seat suspension was nonlinear, with the transmissibility dependent on the magnitude of excitation and distribution of the vibration energy, and that the transmissibility of the seat measured with a rigid mass differed from that measured with human subjects. The phenomena observed during the experimental study were discussed in some details and conclusions were made.
Keywords: Suspension seat; Vibration transmission; Seat transmissibility; Construction machinery
Suspension seat is a key component of construction machinery for isolating the vibration transmitted to the driver and reducing discomfort and health risks. An in-depth understanding of the dynamic characteristics of suspension seats can assist in optimising suspension seat design. The methods, measurement data and findings reported in this paper are not only applied to optimising seating comfort of motor graders, but also useful for improving seating design of other types of construction machinery.
Construction machinery is widely used at roads, railways, ports, mines, and construction and building sites. The characteristics of the machinery (high centre of gravity, high horsepower, and no chassis suspension) and extreme working conditions (rough terrain, engine vibration, and dynamic loads) can result in high magnitude vibrations being transmitted to drivers through the seating. To reduce the vibration transmitted to drivers, construction machinery is commonly equipped with a suspension seat. A laboratory method for measuring, evaluating, and assessing the effectiveness of a suspension seat in reducing the vertical whole-body vibration of the operators of earthmoving machine at frequencies between 1 to 20 Hz is defined in ISO 7096 (2000).
The seats of construction machinery usually have a vertical suspension designed to reduce the vertical vibration experienced by operators. A typical suspension seat has a primary vertical resonance between 1 and 3 Hz and a stroke of up to 100 mm. Boileau and Rakheja [1] studied the transmission characteristics of four suspension seats for log skidders using field tests and laboratory simulations with an inert mass loading the seat. They observed some differences between the field and laboratory measurements and suggested that the difference was caused by the different excitations and different seat loadings. The transmissibility of an air suspension seat was measured and it was reported that the resonance frequency of the transmissibility with a subject weighing 76 kg was the same as that with an equivalent rigid mass of 60 kg (allowing for the mass of the legs not supported on the seat), although the transmissibility at resonance was greater with the mass than with the subject [2]. Wu and Griffin [3] measured the transmissibilities of the suspension, the seat cushion, and a whole suspension seat with a subject (75 kg) and sand bag (56 kg) using a flat constant bandwidth acceleration spectrum over the range 0.5 to 20 Hz with five different vibration magnitudes (0.35, 0.7, 1.05, 1.40 and 1.75 ms-2 r.m.s.). They concluded that only when the input magnitude was high could the resonance frequency and the transmissibility of the whole seat be expected to be similar to the resonance frequency and the transmissibility of the seat suspension. To assist in modelling the frequency response of a locomotive driver seat, the vertical transmissibility of a suspension seat system was measured using an inert load (57.1 kg representing a medium driver sitting mass of 55 kg plus a cushion mass of 2.1 kg) with sinusoidal inputs at various magnitudes (0.5, 1.0 and 2.0 ms-2 r.m.s.) at frequencies between 0.5 and 8.0 Hz [4]. They observed changes in the damped natural frequency with increasing magnitude of vibration, indicating nonlinearity in the suspension. Using the vibration measured on the floor of the locomotive of a passenger train in field tests and computer-generated broadband excitation (1.0 ms-2 r.m.s between 1 and 80 Hz), Smith et al. [5] determined the transmission characteristics in three orthogonal translational directions for two locomotive driver seats. They concluded that without considering the effect of off-axis coupling and other factors, the system transfer matrix evaluated using a multipleinput single-output model would be less than ideal for predicting the low frequency vibration experienced when using a suspension seat.
The main objective of this paper was to study the dynamic characteristics of the suspension seat of a motor grader so as to understand how the seat behaves under different magnitudes and spectra of vibration excitation and provide useful data for modelling and optimisation of the dynamic system of the suspension seat. The seat performance was assessed according to ISO 7096 (2000) [6], and the acceleration transmissibility were measured with various seat and loading conditions. It was hypothesised that the transmissibility of the seat suspension and the complete seat would depend on the magnitude and the spectrum of excitation, and that the transmissibility of the seat with a rigid mass would differ from that measured with human subjects.
Apparatus
The study was conducted in the 1-m vertical simulator in the Institute of Sound and Vibration Research at the University of Southampton. One single-axis Entran ECGS-DO10/V10 accelerometer and two SIT-pads embedded with Entran EGCS-DO- 10V accelerometers were used to measure the acceleration at the seat base (z), the seat surface (z), and the backrest (x). A displacement transducer was used to measure the relative motion of the seat suspension in the vertical direction.
Vibration stimuli, subjects and inert mass
The study involved measurements with subjects and inert masses.
Three male subjects participated in the study. One subject was light (55 kg) and one heavy (93 kg plus 5 kg mass carried in a belt around the waist), consistent with the requirements of ISO 7096 (2000). The third subject had medium weight (76.5 kg). The experiment was approved by the Human Experimentation Safety and Ethics Committee of the Institute of Sound and Vibration Research at the University of Southampton. Informed consent to participate in the experiment was given by all subjects.
The test was also conducted with three inert masses (45, 60 and 75 kg).
The vertical vibration stimuli were broadband random accelerations with approximately flat constant-bandwidth spectra over the frequency range 0.5 to 25 Hz in a duration of 120-second. They were presented at four vibration magnitudes (0.25, 0.5, 1.0, and 1.5 ms-2 r.m.s.).
Data acquisition
The vertical acceleration at the seat base, the vertical and fore-andaft accelerations on the top plate of the suspension, or beneath the inert mass, or at the interface between the seat cushion and subject, and fore-and-aft acceleration at the backrest (for subject tests only) were measured. The relative displacement between the top and bottom plates of the suspension was also acquired. The signals were acquired via 50-Hz anti-aliasing filters with a sampling rate of 512 samples per second. In this paper, only the vertical accelerations are presented and discussed.
Signal processing
Signal processing was conducted using in-house software HVLab with MATLAB R2009b. The number of FFT was 2048 which gave a frequency resolution of 0.25 Hz.
The efficiency of vibration isolation of the seat was evaluated using the seat effective amplitude transmissibility (SEAT) value, determined when the seat was exposed to EM4 excitation according to ISO 7096 (2000). The SEAT value gives an indication of the useful attenuation provided by a seat and is calculated from:
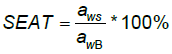 (1)
(1)
where aws is the r.m.s. magnitude of the acceleration measured on the seat surface after frequency weighting by Wk, according to ISO 2631-1 (1997), and awB is the r.m.s. magnitude of the acceleration measured on the vibrator platform and also weighted with Wk.
The vibration transmission was characterised by calculating acceleration transmissibility from seat base to seat surface or backrest, using the cross-spectrum density method:
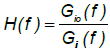 (2)
(2)
where Gi(f) was cross spectral density of the input (vertical or foreand- aft acceleration at the seat base) and output (vertical acceleration at the seat surface or fore-and-aft acceleration at the backrest) and Gi(f) was the power spectral density of the input. The coherence function which was computed (Equation 2) to show how the output accelerationlinearly accounted for by the input acceleration:
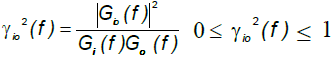 (3)
(3)
In the above equation G∞(f) was power spectral density of the output acceleration.
Transfer function H(f) contains both modulus and phase information:
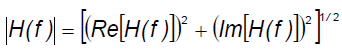 (4)
(4)
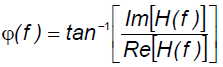 (5)
(5)
Test procedure and method
The suspension seat was assessed with ISO 7096 (2000) for its damping characteristics and isolation efficiency using EM4 input spectrum. During the damping test conducted according to ISO 7096 (2000), the seat was loaded with an inert mass of 75 kg. It was then excited by a sine sweep (0.5 - 3 Hz) from low to high frequency and back to the low frequency again. The frequency sweep had duration of 92 s and was performed at a constant peak-to-peak displacement of 37.5 mm (about 40% of the total suspension stroke). The transmissibility at the resonance was calculated at 0.125 Hz increments over the range 0.5 to 3.0 Hz based on unweighted r.m.s. values of the vertical accelerations on the seat and the platform.
After the seat performance test with ISO 7096 (2000), a series of measurements for acceleration transmissibility in various conditions were conducted: (i) the seat suspension loaded with rigid masses (Figure 1a), (ii) the complete seat loaded with rigid masses (Figure 1b), and (iii) the complete seat loaded with light, medium, and heavy subjects (Figure 1c).
Dynamic performance according to ISO 7096 (2000)
The resonance frequency and the corresponding maximum transmissibility obtained during the damping test were 1.38 Hz and 1.70, respectively. According to ISO 7096 (2000) the acceptance value of the maximum transmissibility for EM4 machine class should be less than 1.5.
Table 1 lists the average results of three repetitive measurements conducted using the simulated input vibration (ISO 7096:2000 class EM4). The SEAT values were lower than the acceptance value (i.e. less than 1.1) as required by ISO 7096.
| Subject | Unweighted acceleration on the platform ms-2 r.m.s | Wk weighted acceleration | SEAT values | |
|---|---|---|---|---|
| Platform ms-2 r.m.s. | Seat ms-2 r.m.s. | |||
| Heavy | 0.99 | 0.64 | 0.58 | 0.91 |
| Light | 1.01 | 0.66 | 0.68 | 1.02 |
Table 1: Vertical vibration characteristics of the seat according to ISO7096:2000 Class EM4.
Vibration transmissibility of the seat suspension with inert masses
The modulus, phase, and coherency of the transmissibility between the vertical accelerations at the base and the top of the suspension supporting the inert mass are shown in Figure 2, while the relative displacements of the suspension are shown in Figure 3.
The modulus of the transmissibility generally exhibited one primary peak in the frequency range 0.5 to 25 Hz. The peak was around 21 Hz when the magnitude of excitation was low (0.25 ms-2 r.m.s.) and shifted from about 21 Hz to 16 Hz with the inert mass increased from 45 kg to 75 kg. Increasing the vibration magnitude progressively reduced the peak frequency to below 5 Hz, although the peak also became less clear. The phase lag generally increased with increasing magnitude of vibration. The corresponding coherency also reduced with increasing the magnitude of vibration.
When the vibration magnitude was low (0.25 and 0.5 ms-2 r.m.s.), the relative displacement of the suspension was less than ±1 mm (Figure 3). The suspension travel increased with increasing magnitude of vibration and reached about ±8.5 mm with vibration excitation at 1.5 ms-2 r.m.s.
Vibration transmissibility of the complete seat with inert masses
The modulus, phase, and coherency of the transmissibility between the vertical accelerations at the seat base and the seat cushion for the complete seat supporting the inert mass are shown in Figure 4, while the relative displacements of the suspension shown in Figure 5.
The modulus of the transmissibility exhibited a single clear primary peak in the frequency range 5 to 10 Hz and a second peak between 10 to 20 Hz. The modulus and frequency of the primary peak reduced as the magnitude of vibration increased (from 0.25 to 1.5 ms-2 r.m.s.) and reduced as the inert mass increased (from 45 to 75 kg). With a vibration magnitude of 1.5 ms-2 r.m.s., the primary peak became indistinct with the peak frequency lower than 2 Hz. As the magnitude of vibration increased, the phase lag increased at lower frequencies and the coherency was reduced at all frequencies.
Table 2 shows the frequency of the primary peak and the corresponding transmissibility with various vibration magnitudes when tested with the same inert mass (75 kg) used in the ISO 7096 (2000) damping test.
| Magnitude of input acceleration. (ms-2 r.m.s) | 0.25 | 0.5 | 1 | 1.5 |
| Primary peak frequency (Hz) | 7.38 | 6.13 | 3.25 | 1.38 |
| Transmissibility at the primary peak frequency | 2.73 | 1.82 | 1.19 | 1.2 |
Table 2: Primary peak frequency and transmissibility of the complete seat with 75 kg mass.
The relative displacements of the suspension were small (maximum of ± 1.5 mm) when the vibration magnitude was low (0.25 and 0.5 ms-2 r.m.s.) but increased as the vibration magnitude increased (about ± 11 mm with 1.5 ms-2 r.m.s., Figure 5).
Vibration transmissibility of the complete seat with subjects
With the complete seat supporting the light, medium, and heavy subjects, the modulus, phase, and coherency of the transfer function between the vertical accelerations at the seat base and the seat cushion are shown in Figure 6, while the relative displacements of the suspension are shown in Figure 7.
The modulus of the transmissibility exhibited three peaks with a primary peak in the frequency range below 6 Hz, a second peak in the range 7 to 15 Hz, and a third peak between 15 and 25 Hz. The moduli and frequencies of the peaks reduced with increasing vibration magnitude (from 0.25 to 1.5 ms-2 r.m.s.) and with increasing subject weight from 55 to 93 kg. With a vibration magnitude of 1.5 ms-2 r.m.s., the modulus at the primary peak was reduced and the peak frequency shifted to lower than 2 Hz, close to the resonance frequency of 1.38 Hz identified during the ISO 7096 (2000) damping test. As the magnitude of vibration increased, the phase lag increased and the coherency was reduced.
The relative displacements of the suspension were small (maximum of ±1.0 mm) when the vibration magnitude was low (0.25 and 0.5 ms-2 r.m.s.) but increased as the vibration magnitude increased and reached to about ±10 mm when the magnitude was 1.5 ms-2 r.m.s. (Figure 7).
The vibration characteristics of the suspension seat, including SEAT values calculated in a way analogous to that used during the simulated input vibration test with ISO 7096 (2000) are shown in Table 3.
| Complete seat with heavy subject: | ||||
|---|---|---|---|---|
| Magnitude of the input acceleration (ms-2 r.m.s.) | 0.25 | 0.5 | 1 | 1.5 |
| Primary peak frequency (Hz) | 4.88 | 4.38 | 2.25 | 1.38 |
| Unweighted acceleration at the seat base in the range 0.89 to 11.22 Hz (ms-2 r.m.s.) | 0.15 | 0.3 | 0.6 | 0.91 |
| Wk weighted acceleration at platform (ms-2 r.m.s) | 0.14 | 0.28 | 0.56 | 0.84 |
| Wk weighted acceleration at seat (ms-2 r.m.s.) | 0.18 | 0.3 | 0.43 | 0.49 |
| SEAT value | 1.24 | 1.06 | 0.77 | 0.58 |
| Complete seat with light subject: | ||||
| Magnitude of the input acceleration (ms-2 r.m.s.) | 0.25 | 0.5 | 1 | 1.5 |
| Primary peak frequency (Hz) | 5.25 | 4.37 | 3.62 | 2.25 |
| Unweighted acceleration at the seat base in the range 0.89 to 11.22 Hz (ms-2 r.m.s.) | 0.16 | 0.32 | 0.63 | 0.93 |
| Wk weighted acceleration at platform (ms-2 r.m.s.) | 0.15 | 0.3 | 0.59 | 0.87 |
| Wk weighted acceleration at seat (ms-2 r.m.s.) | 0.17 | 0.32 | 0.51 | 0.61 |
| SEAT value | 1.13 | 1.04 | 0.86 | 0.7 |
Table 3: Vibration characteristics of the seat measured with heavy and light subjects and calculated in a way analogous to that used during the simulated input vibration test with ISO 7096 (2000).
Comparison of the transmissibility between the suspension and complete seat
The transmissibility of the vertical acceleration from the seat base to the seat surface measured with the complete seat loaded with inert masses showed a lower primary peak frequency than the transmissibility of the suspension alone with the same loading condition (the first two rows in Figure 8). This was mainly due to the combination effect of the compliance of the seat cushion and the extra mass of the seat and backrest cushion assembly (about 20 kg) on the top of the suspension. The complete suspension seat with inert mass can be idealised as a twodegree- of-freedom system, while the suspension alone with inter mass as a single-degree-of-freedom system.
With low magnitude vibration, the suspension was locked up by friction and hence the overall dynamic performance of the complete seat was dominated by the dynamics of the seat cushion, yielding the primary resonance frequency in the region of 7-8 Hz with a modulus of the transmissibility in excess of 3 (Figure 4). With increasing magnitude of vibration, both the resonance frequency and the associated modulus of the transmissibility reduced and the transmissibility became closer to that measured with the seat suspension alone (see last two rows of Figure 8). When a suspension seat is subjected to high magnitude vibration the dynamics of the suspension becomes dominant and the influence of the cushion dynamics becomes less important.
The transfer function obtained with the complete seat supporting 75 kg inert mass during random broadband excitation showed the same primary peak frequency (1.38 Hz, Table 2) as the ISO 7096 (2000) damping test, but with lower maximum transmissibility (1.20) than the damping test (1.70). The ISO 7096 (2000) damping test employed a sinusoidal sweep over the range 0.5 to 3 Hz with an acceleration magnitude of 1.55 ms-2 r.m.s., whereas the transfer function was determined with random broadband excitation between 0.5 and 25 Hz with 1.5 ms-2 r.m.s. The difference in the peak transmissibilities in the two tests may be due to the difference in the excitations applied and the fact that the suspension seat is nonlinear.
Comparison of the seat transmissibility between with subject and with inert mass
The transmissibility of the complete suspension seat supporting a subject differed from the transmissibility of the seat supporting an inert mass of equivalent weight (Figure 9). The transmissibility with an inert mass showed mostly one primary peak and seldom a secondary peak. In addition to the primary peak, the transmissibility with subjects showed second and even third peaks, especially when the vibration magnitude was low (0.25 and 0.5 ms-2 r.m.s.).
The moduli of the transmissibilities of the complete seat with inert masses exposed to low magnitude vibration were much higher than with subjects. With increasing vibration magnitude, the transmissibilities of the complete seat with inert masses tended to converge towards those with subjects. When the vibration magnitude reached 1.5 ms-2 r.m.s., the two transmissibilities became very similar (Figure 9). These observations are consistent with the findings of Wu and Griffin [3] and others (e.g., Fairle et al. [2]; Toward MGR et al. [7]). Dynamic characteristic of the seat with a mass is different from that of the seat with a subject. At low magnitudes, the suspension is almost locked and the response is dominated by the cushion dynamics. With an inert mass, the effective stiffness of the seat–mass system is higher but the effective damping of the system is lower than the corresponding values of the seat-body system. This is because the human body is a multi-degree-of-freedom and highly damped system resulting in relatively low effective stiffness and high effective damping of the seatbody system. At high magnitudes, on the other hand, the friction in the suspension is overcome and the suspension comes into play. As a result, both the suspension and seat cushion become effective, and the effective damping and stiffness or dynamics of the two systems converge, resulting in the seat transmissibility in the seat-mass system close to that of the seat-body system. At the lower frequencies, the apparent mass of the body is similar to the inert mass, giving similar transmissibility.
Comparison of the transmissibility between random broadband and ISO 7096 EM4 inputs
As can also be seen from Figure 10, the primary resonance frequency of the seat transmissibility measured with the seat-body system exposed to broadband random excitation at 1.5 ms-2 r.m.s. (Table 3) is similar to that determined in the simulated vibration input test using ISO 7096 (2000) Class EM4 excitation. The transmissibility with ISO 7096 (2009) EM4 input spectrum is only presented up to 5 Hz because at the frequencies above 5 Hz the coherency of the transmissibility was found very low, owing to low vibration energy in this frequency band. Inspection of Tables 1 and 3 reveals that in the ISO 7096 (2000) simulated input vibration test the unweighted acceleration r.m.s. values at the seat base was 0.99 ms-2 for the heavy subject and 1.01 ms-2 for the light subject, close to the corresponding values of 0.91 and 0.93 ms-2 r.m.s. in the laboratory measurement of seat transmissibility with broadband random excitation at 1.5 ms-2 r.m.s.. However, the two tests yielded different SEAT values. Although the excitations were both random vibration with similar acceleration magnitudes in the frequency range between 0.89 and 11.22 Hz, they had different frequency-weighted accelerations at the seat base and on the seat. For the EM4 test, the weighted accelerations were 0.64 and 0.66 ms-2 r.m.s. at the seat base and 0.58 and 0.68 ms-2 r.m.s. at the seat surface, for the heavy and light subjects, respectively (Table 1). For the laboratory transmissibility tests, these weighted magnitudes were 0.84 and 0.87 ms-2 r.m.s. at the seat base and 0.49 and 0.61 ms-2 at the seat surface, for the heavy and light subjects, respectively (Table 3). The difference is likely due to different distributions of the vibration energy over the frequency range in the two tests (Figure 11).
The vibration excitation must be sufficient to overcome friction existing in a seat suspension mechanism before it can function properly as a vibration isolator. A seat suspension has nonlinear characteristics that depend on not only properties of the suspension components but also the suspension structure.
The acceleration transmissibility of a suspension seat supporting subjects can be very different from that with the seat supporting an inert mass. With an inert mass, the transmissibility at resonance may be greater than with a human subject, especially with low magnitudes of excitation. The influence of the biodynamics of the human body should not be ignored and needs to be taken into consideration when optimising the dynamics of seat suspensions.