Basic dynamics of rockets has been well understood for a long time [1]. In this short Note we focus on the effects of flexibility of long slender rockets, and in particular on possibilities of buckling due to thrust on an elastic booster vehicle with rapid mass loss. To describe the dynamics, we define a body reference frame B moving in a Newtonian frame N, and introduce generalized speeds [2] for the rotation of B in N and the velocity in N of a point O fixed in B, as follows:

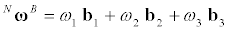(1)

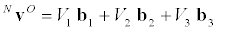(2)

Use of assumed vibration modes of the body, defined in frame B, yields for the position and velocity of a particle P of the body,

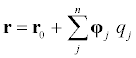(3)

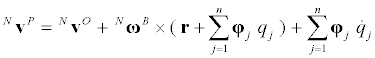(4)

Here 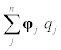describes the elastic deformation in a Rayleigh-Ritz sense [3] using generic modes of vibration at a node in a finite element model of the booster body. Introducing efficient generalized speeds [4], for elastic deformation, σ_j associated with the j-th mode of vibration,

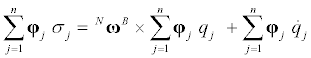(5)

Renders Equation (4) free of the vibration mode coordinates, q_j, leading to the simplification:

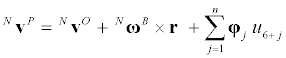(6)

Kinematical equation for modal coordinates follow 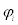from dotmultiplying Equation (5) by and integrating over the body mass at time t.

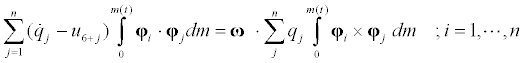(7)

Equation (7) can be written in matrix form as

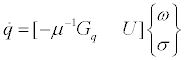(8)

Here q and σ are n×1 column matrices, μ is a nxn matrix of generalized modal mass, U is a nxn unity matrix, and G_q is a n×3 matrix shown below, involving 3×3 skew-symmetric matrices corresponding to vector cross-products of the vector , k=1,…,n:

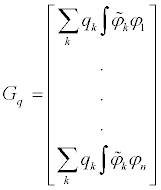(9)

Kane’s equations for variable mass, can now be formed by extending those for the particle model of [5] to flexible bodies, and are written for the 6+n generalized speeds as follows:

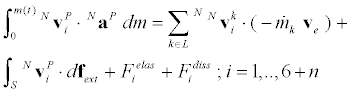(10)

Here 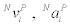are the i-th partial velocity [2] and acceleration of P, respectively, obtained directly as the coefficient vectors from Equation (4), 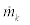is the mass loss rate and v_e is the mass ejection velocity, with sum of representing thrust T; df_ext is the external (gravity and aerodynamic) force, 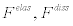are respectively, the generalized elastic and dissipation forces, with the former derivable from the potentials due to elastic and geometric stiffness [6].

Equation (10) is expressed in terms of eight modal integrals matrices, the elements of which are of the following form, that can be evaluated for the time-varying mass m(t) = m_f g(t), where m_f is the final mass, and k=1,..,8 and j=1,..,n (the total number of modes).

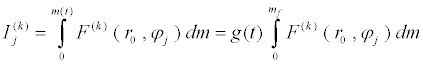(11)

We make an assumption here that the Rayleigh-Ritz vibration modes remain meaningful for rapid mass loss. Note that the modal integrals are evaluated only for the final mass m_f. Instantaneous mass is represented by a Hermite polynomial in terms of initial mass loss rate and initial and final mass, with

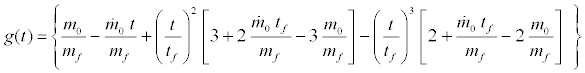(12)

Finally, note that the generalized forces derivable from a potential function P and dissipation function D follow from Kane’s theory [2] as the matrix equation

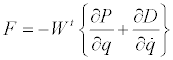(13)

Here W is the matrix that relates the rate of change of the generalized coordinates, by definition, to all the generalized speeds, in the kinematical equations of the general form,

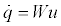(14)

Based on nominal elasticity and geometric stiffness due to thrust T, respectively due to elastic and thrust-dependent stiffness, Kg, [6], we have:

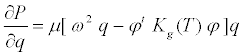(15)

Note that thrust opposing acceleration would actually provide a buckling effect. Now assuming normal vibration mode damping one has

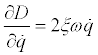(16)

Use of Equations (13-16) and Equation (8) lead to the generalized forces due to elasticity and damping in the rotational and modal generalized speeds as

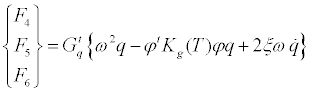(17)

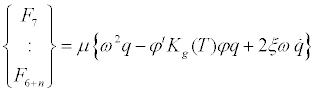(18)

Now the final equations of motion of the rocket emerge as follows, with Equation (10) represented in matrix form as,

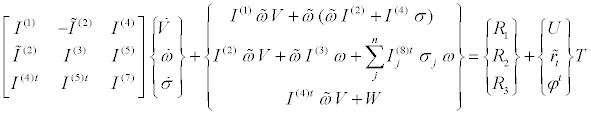(19)

Here R₁, R₂, R₃ are all terms representing forces other than thrust, namely, contributions from gravity, aerodynamics, normal and geometric stiffness, and damping. To these are added the kinematical equations, Equation (8), and the equations relating the inertial x-, y-,zdisplacements rates to the body components of velocity, and the Euler parameter or quaternion rate equations to the body components of angular velocity [7].

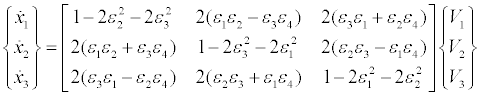(20)

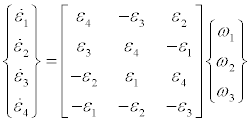(21)

Because of the usual classified nature of actual applications, only idealized simulation results are presented here. Sample results of simulation for the flight of a flexible body rocket are shown in Figures 1-4. Figure 1 shows the flight altitude time history for the rocket, and Figure 2 its attitude history, as indicated for example, by the second quaternion of an Euler parameter attitude description. Figure 3 shows the time-history of the third-assumed mode of vibration of the rocket. Figure 4 shows the mass depletion rate, bringing out the crucial variable mass character of the rocket. The results show the generality of the mathematical equations provided in this paper. The formulation itself should be useful for nonlinear control design of the flight of a rocket that can bend in flight.

Figure 1: Altitude vs Time.

Figure 2: Attitude Quaternion 2 vs Time.

Figure 3: Mode 3 vs Time.

Figure 4: Total Mass vs Time.

We have extended Kane’s equations for variable mass to flexible bodies, to simulate the dynamics of a flexible rocket. The features include computing geometric softness due to thrust, and can thus simulate possibilities of buckling. The choice of motion variables and the interpolation scheme for evaluating modal integrals make the formulation time-efficient.