Journal of Drug Metabolism & Toxicology
Open Access
ISSN: 2157-7609
+44-77-2385-9429
ISSN: 2157-7609
+44-77-2385-9429
Research Article - (2016) Volume 7, Issue 4
P-glycoprotein (P-gp) is a multispecific transporter which has a natural detoxification role. The inhibition of substrate transport by P-gp can be presented by a number of parameters, including percentage inhibition and IC50. Inhibition constant, Ki, is believed to be a more universal parameter allowing easy comparison of data from different substrate conditions. The aim of this investigation was to use molecular descriptors of the inhibitors, docking scores, and the parameters of the probe substrate for the development of Quantitative Structure-Activity Relationships (QSARs) for the prediction of P-gp inhibition constants. QSARs were developed using a number of data mining and pre-processing feature selection methods. A chi-square based regression tree followed by a boosted trees model were the most accurate in the estimation of Ki. The selected models incorporated molecular descriptors of the inhibitors followed by the molecular descriptors of probe substrates, whereas no docking scores were selected by the models. Potent P-gp inhibitors showed higher lipophilicity and molecular weights than those molecules defined by Oprea's rule.
Keywords: P-glycoprotein; QSAR; Docking; Inhibitor; Substrate
BT: Boosted Trees; CART: Classification and Regression Tree; CHAID: Chi-square Automatic Interaction Detector; I-tree: Interactive Tree; MARS: Multivariate Adaptive Regression Splines; MDR: Multidrug Resistance; P-gp: P-glycoprotein; QSAR: Quantitative Structure-Activity Relationships; RF: Random Forest; RT: Regression Tree
One in four deaths in the United States is due to cancer and recently the American Cancer Society reported a total of 1,660,290 new cancer cases and 580,350 cancer deaths are projected to occur in the United States in 2013 [1]. The failure of cancer treatment can be attributed to a variety of different pharmacological and clinical reasons; but one major cause of the treatment failure is Multidrug Resistance (MDR) to chemotherapeutics [2]. MDR mechanisms can result in resistance to a number of structurally and functionally unrelated chemotherapeutic agents. The MDR behaviour is mainly linked to the activity of transmembrane efflux pumps such as P-glycoprotein 1 (P-gp/ABCB1), breast cancer resistance protein (BCRP/ABCG2) and multidrug resistance-associated protein 1 (MRP1/ABCC1), which are members of ATP-Binding Cassette transporter family [3]. P-gp, also known as multidrug resistance protein 1 (MDR1), is a well-studied glycoprotein that demonstrated its function as a transporter of hydrophobic drugs, lipids, steroids and metabolic products [4].
Apart from its role in multidrug resistance, P-gp has a profound role in pharmacokinetics, affecting drug absorption, distribution and excretion [5]. It is found in high amounts at the apical surface of epithelial cells lining the colon and small intestine and in hepatocytes, pancreas ductules, proximal tubules in kidneys and the adrenal gland [6,7]. P-gp is also known to play a major role in transporting compounds out of the brain in the blood brain barrier [8]. In the BBB, only suitably lipophilic compounds can diffuse across the endothelial cells and enter the brain. However, a high proportion of P-gp that surrounds this area of the brain prevents their accumulation by distributing substrates back into the blood circulation [8]. In the gastrointestinal tract and in hepatocytes, P-gp is responsible for the efflux of drugs back into lumen/bile, thus reducing the bioavailability of substrate drugs [9]. Similarly, in kidneys, P-gp is located primarily in glomerular mesangium cells and the apical membrane of proximal tubule epithelia and plays a significant role in the tubular secretion of organic cations [9].
Substrates of P-gp can have molecular weights ranging from 250-1850 Da, different ionization states, acid/base properties, hydrophobicities or amphipathic properties [10]. There are drugs and herbal products that can affect the function of P-gp transporters and the number of drugs that are found to be the P-gp substrates is continuously growing. For instance, rifampin (an antituberculosis drug) induces the intestinal expression of P-gp [11]. Due to the broad substrate specificity, drug-drug interactions involving P-gp are very likely [5]. Drug-drug interaction is an important issue observed in cancer patients, especially because they often receive multiple medications concurrently with complex chemotherapy regimens [12]. Due to the potential significance of P-gp in drug interaction, the FDA has urged that every new molecular entity should be routinely checked for possible interactions with P-glycoproteins [13].
Overexpression of P-gp in cancer cells contributes significantly to the resistance of cancer cells against chemotherapeutic agents [14]. Pgp is able to export a number of structurally diverse anticancer agents including anthracyclines, epipodophyllotoxins and vinca alkaloids. As a result, P-gp has been suggested as a viable target for inhibition in the treatment of MDR cancer [15]. Drugs such as actinomycin-D and azithromycin can strongly block the P-gp and limit the efflux of P-gp substrates. Inhibitors that block the transport of chemotherapeutics or other compounds may act as competitive or non-competitive inhibitors [16]. In recent years, the inhibitory activity against P-gp has been tested in many compounds in order to overcome P-gp mediated resistance of cancer cells to the chemotherapeutics [17].
Given the clinical relevance of P-gp, it is important to elucidate the mode of interaction with the ligands of this enzyme. Higginis and colleagues proposed the "hydrophobic vacuum" model to explain the polyspecificity of P-gp [18]. In the proposed model, the hydrophobic substrates enter the transmembrane domain of P-gp and are transported outside the cell. A recent study by Aller et al. [19] provided a detailed structural description of mouse P-gp, which indicates a substantial internal cavity comprising mostly hydrophobic and aromatic residues. Despite the substrate promiscuity, several studies have been valuable in identifying structure activity relationships for the modulators. Evidences from x-ray crystallography, [19] chromatography [20] and several biochemical techniques [21,22] suggest the presence of multiple substrate-binding sites and inhibitory mechanisms, which may be the cause of substrate promiscuity. As a result, it may be necessary to generate more than one pharmacophore for P-gp, one for the inhibitors of each probe substrate [23]. Similarly, structure-activity relationships may be different for the inhibition of efflux of different substrates, or different inhibition mechanisms. Using IC50 as the measure of inhibition potency is the other additional reason for the need for different models for P-gp inhibition when different substrates and/or substrate conditions have been used for IC50 measurement. The use of IC50 (concentration of inhibitor required for 50% inhibition) has the disadvantage of not allowing data from different substrate conditions to be compared easily. Unlike IC50, the inhibition constant, Ki, is a more universal parameter that is standardised according to the substrate concentration and Km values [24].
The first aim of this investigation was to use, several data mining techniques to enable development of universal models for the prediction of P-gp inhibition constant (Ki). In particular, Classification and Regression Tree (CART) is a powerful decision tree technique that can select significant features for partitioning of the data. The use of molecular descriptors for the substrates in addition to the inhibitor parameters can be useful for splitting Ki data if the substrate type has an effect on the measured Ki values. The second aim examined, docking scores as a complementary parameter to investigate the significance of interaction energy between the inhibitors and P-gp in the models for the estimation of the binding constants.
Dataset
IC50 and Ki values for P-gp inhibitors were collated from the literature [23,25-47]. IC50 values of P-gp inhibitors were used to calculate the Ki values using the Cheng-Prusoff equation below.
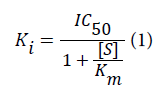
In this equation, [S] is the substrate concentration and Km is the Michaelis-Menten constant for the substrate (the concentration of substrate at which enzyme activity is at half maximal). Km values for the substrates not reported in the publication were obtained from the authors through personal communication. The rationale behind converting the IC50 values to Ki values is that the Ki is a more universal scale, which, in theory, should be independent of the substrate used.
In case there were several IC50/Ki values available for a single inhibitor from different sources, the average Ki values were used, unless the probe substrate was different. If there was a significant difference in the reported IC50/Ki values, we contacted the authors to find out if they could provide an explanation for the observed differences before using the reported values. In total, the dataset consisted of Ki values for 219 unique inhibitor/substrate pairs, with data measured in different cell systems, including human colon carcinoma cell line (Caco-2), Madin-Darby canine kidney cells (MDCK)-MDR1, MDCK II-MDR1, K562-MDR, MDR1 transfected LLC-PK1 and P388 lymphoma cells. Caco-2 and MDCK was the most common cell lines used in our dataset. The inhibitors in the dataset are from different chemical/pharmacological classes, such as anticancer and anti-HIV agents, statins, antiretrovirals, cephalosporines, ergopeptides, antipsychotics, opioids, NSAIDs, analgesics, and antiarithmetic drugs. The dataset is presented in the Supporting Information I.
Molecular descriptors
Molecular descriptors were calculated for the inhibitors and the substrates using ACD Labs/LogD Suite version 12 (Advanced Chemistry Development, Inc. Ontario, Canada), TSAR 3D version 3.3 (Accelryls Inc. San Diego, CA), MOE version 2011.10 (Chemical Computing Group Inc. Montreal, Canada) and Symyx QSAR software (Accelryls Inc. San Diego, CA). The fractions of compounds that are ionised at pH 7.4 as acid (FiA), as base (FiB), or (for zwitterionic compounds) as acid and base (FiAB), and the fraction unionised (Fu) were calculated from the lowest acidic and the highest basic pKa values [48].
P-gp-ligand docking
Docking energy for all inhibitors was calculated using MOE software and was used as an additional molecular descriptor for the inhibitors. For docking, the x-ray structure of mouse P-gp was obtained from the protein data bank (PDB code 3G60) [http://www.rcsb.org]. The use of this PDB structure was due to a previous docking investigation that showed better scoring poses using mouse 3G60 structure in comparison with the other two mouse P-gp structures (PDB codes: 3G61 and 3G5U), or the human homology model of P-gp [49]. Moreover, it has been shown from BLAST alignment studies that human and mouse P-gps have 87% overall sequence identity and 100% identity within the binding cavity with the exception of mouse Ser725 and human Ala729 [50]. It should be noted that 3G60 structure of mouse P-gp was co-crystalised with a ligand and the complex had two stereo-isomers of cyclic hexapeptide inhibitors, cyclic-tris-(R)-valineselenazole (QZ59-RRR) and cyclic-tris-(S)- valineselenazole (QZ59-SSS) in the active site [19]. The protein was protonated and protonatable residues were titrated using the default software parameters. For the ligands, following the atomic charge calculation using SCF optimization (AM1 Hamiltonian), molecular structures of the ligands (P-gp inhibitors) were optimised. In enzymeligand docking, default parameters of the software were used for ligand interactions. These are energy cut-off for H-bond and ionic interactions of -0.5 kcal/mol and maximum distance for non-bonded interactions of 4.5 Å. In the MOE dock panel, the placement method was Triangle Matcher, the scoring methodology was set to London dG as the first and the second scoring functions, the refinement methodology was set to Forcefield, and the 30 best scoring poses and the mean energies were retained. The binding site was defined in MOE software using the co-crystallised ligand QZ59-RRR. This docking methodology has been previously validated for P-gp [51].
Model development and validation
To perform QSAR analyses, P-gp inhibitors were divided into validation and training sets. To divide the inhibitors, they were ordered with ascending Ki values and then from every five compounds, four were randomly allocated into the training and one into the validation set. This validation set remained external and was not used at any stage of the model development. The process of allocating chemicals into training and validation sets ensured similar Ki ranges for the validation and training sets. In this way, the training and external validation data sets consisted of 176 and 43 compounds, respectively. In addition to using this external validation set, all the model development methods employed a ‘cross-validation’ procedure that allowed leaving 1/7th or 1/10th of the compounds out (Leave-Many-Out) by random splitting of the training set compounds. This ‘V-fold’ cross validation was used by the software for decisions on the complexity of models and model optimization in terms of their accuracy for the internal validation set. Besides, ‘Cross-validate tree sequence’ was used in addition to V-fold cross-validation to ensure the validity of each level of the tree for accurate prediction of log Ki in both training and validation sets.
STATISTICA Data Miner version 11 was used for the statistical analysis. Statistical methods consisted of decision tree methods and ensemble methods, including Classification and Regression Tree (CART), Chi-square Automatic Interaction Detector (CHAID), Boosted Trees (BT), Random Forest (RF) and Multiple Linear Regression (MLR). As the multiple linear regression models using stepwise regression descriptor selection did not produce an acceptable level of accuracy, Multivariate Adaptive Regression Splines (MARS) model was developed. Log Ki was the dependent variable and the predictors were selected by the embedded feature selection methods in CART, CHAID, BT and RF from all the molecular descriptors and docking scores available for the inhibitors and substrates. For the development of the MARS model, several pre-processing feature selection techniques were examined.
Regression Tree (RT) and Interactive tree (I-tree) using CART
STATISTICA version 11 (StatSoft Inc. Tulsa, OK) was used to develop the RTs using the CART algorithm. The analysis has an embedded feature selection method, which picks the most significant molecular descriptors for splitting the data into two most homogeneous groups (called branches or nodes) and carries the splitting until all the data in the nodes have the same value or a stopping criterion has been fulfilled. By doing so, it builds an optimal tree structure to predict continuous dependent variables via V-fold cross-validation. The size of a tree in CART analysis is an important issue, since an unreasonably big tree can lead to overfitting and can make the generalisation to external data and the interpretation of the model more difficult. Several stopping criteria were examined, including the default settings in STATISTICA. The default stopping criteria were minimum number of cases of 24 to allow further splitting and the maximum number of nodes set to 100. The default V-value of 10 or seven was used in the V-fold cross-validation and the standard error for the internal test set was used to check the reliability of the resulting RTs.
Interactive tree is a CART-style tree, which allows for the molecular descriptors to be selected manually by the operator. This tool is useful when investigating the effect of certain variables/molecular descriptors on the property under investigation, in this case log Ki . In I-tree, apart from the usual V-fold cross-validation procedure, another crossvalidation option, “Cross-validate tree sequence” was also applied. This validation method is applied to the entire tree sequence, instead of just the final tree in V-fold cross-validation [52].
Chi-square Automatic Interaction Detector (CHAID)
CHAID is one of the oldest tree methods, initially suggested by Kass in 1980 [53]. This tool performs multi-level splits, where CART uses binary splits. CHAID is well suited for large data sets. Cross validation was used to safeguard against overfitting the CHAID tree. STATISTICA default setting for stopping criteria were used, including minimum number of cases for splitting of 22, maximum number of nodes of 1000, probability for splitting of 0.05 and probability for merging of 0.05. To test the statistical significance of splits, CHAID computes a Bonferroni adjusted P-value for the respective descriptor [52]. Bonferroni adjustment is an option in CHAID, used to control the type one error rate (familywise error rate) when testing multiple hypotheses. It is usually accomplished by dividing the alpha level by the number of tests being performed (usually 0.05/n). In this work, we used a Bonferroni adjustment as our preliminary results showed lower cross validation error when this adjustment was used.
Boosted Trees (BT)
BT analysis in STATISTICA generates a series of very simple boosting regression trees (BT), where each successive tree is built for the prediction of residuals of the preceding tree. Each of these trees has weak predictive accuracy but using the weak predictors together can create a strong predictor [52]. The default values for learning rate, the number of additive terms (number of trees), random test data proportion (percentage of data points in internal testing pool) and subsample proportion were 0.1, 200, 0.2 and 0.5, respectively. Various subsample proportions of 0.45, 0.50, 0.55 and 0.60 were also examined in combination with the learning rates of 0.10, 0.03, 0.05 and 0.08. The best model was selected based on the performance indicators for the internal validation set. The seed for random number generation, which controls which cases are selected in sampling, was set to one. The maximum number of nodes was set to three, meaning that each tree will have one binary split.
Random Forest (RF)
An RF model is an ensemble of tree predictors such that each tree depends on the values of a random vector (a random selection of molecular descriptors and training set compounds) sampled independently. The method builds a series of simple trees where the predictions are taken to be the average of the predictions of all the trees [54]. Various subsample proportions of 0.45, 0.50, 0.55 and 0.60 were examined while the number of predictors (to be randomly considered at each node) was 9. The random test data proportion was 0.3 for the internal validation and number of trees was 100. The default settings were used for stopping conditions including minimum number of cases, maximum number of levels, minimum number in child node and the maximum number of nodes of 5, 10, 5 and 100, respectively. The best model was selected based on the estimation error for the internal test data.
Multivariate Adaptive Regression Splines (MARS) model
MARS is a non-parametric regression procedure that constructs a relation between the dependent and independent variables from a set of coefficients and basic functions that are entirely driven from the regression data [55]. It is a very flexible technique that automatically models non-linearities and interactions between variables. The nonlinearities (knots) are represented by the so-called ‘hinge functions’; these are expressions of the type ‘max (a,b)’ where the value of this expression will be ‘a’ if ‘a>b’, or else ‘b’. Interactions between each variable pairs can also be expressed in the formula. MARS model is developed by stepwise addition of basic functions in pairs (forward pass) to reduce the sum-of-squared residual error and then step-bystep removal of the least significant terms to achieve better generalisation (backward pass). Model subsets are compared using the Generalized Cross-Validation (GCV) criterion. GCV is the adjusted form of residual sum-of-squares that penalises the addition of knots in order to limit the model flexibility and overfitting.
In addition to using all the molecular descriptors in MARS analysis and allowing MARS to select the significant descriptors, we performed a pre-processing feature selection to select a limited number of molecular descriptors for use in MARS analysis. Feature selection methods were the Chi-square method as implemented in STATISTICA [52], stepwise regression analysis and variable importance rank from RF and BT analyses. The Chi-square-based feature selection in STATISTICA picks a subset of descriptors from the descriptor pool without assuming that the relationships between the predictors and the dependent variables are linear or even monotone. In this feature selection, the range of continuous variable values was divided into 10 intervals. The six best descriptors picked by STATISTICA feature selection, the six best descriptors selected by stepwise regression analysis, as well as the top 5, 10, 15, 20 and 25 descriptors picked by RF, and the top 5, 10 and 15 descriptors picked by BT were examined in separate MARS analyses and the resulting models were compared in terms of the prediction error. In MARS analysis, the default model specifications for maximum number of basic functions, degree of interactions, penalty and threshold were 21, 1, 2 and 0.0005, respectively.
P-gp is an important polyspecific transporter protein that can significantly affect the pharmacokinetics of various pharmaceuticals as well as the effectiveness of chemotherapeutics. In this investigation, a large dataset of inhibition constant was collated to investigate the development of a universal model for P-gp inhibitors. To help overcome the problem of heterogeneity of the data from various laboratories, that incorporate various substrates at differing concentrations in the design of their experiments, several strategies were implemented. First, the IC50 values were converted to Ki values, which is a more comparable measure of inhibitory activity. Secondly, the molecular descriptors of the probe substrates were also used in the analyses and model development process. Third, the non-linear decision trees and MARS methods were employed that are flexible; therefore, in theory they should be able to deal with more heterogeneous data.
Various decision trees and ensemble models as well as MARS model were developed for the prediction of P-gp inhibition constant. Table 1 summarises the selected models developed using various statistical methods. All models obtained were cross-validated and pruned accordingly. The selected models were those with the lowest standard error for the internal test set. Models listed in Table 1 resulted from various feature selection and data analysis methods. The majority of these models can be easily interpreted in terms of the molecular characteristics required for an effective P-gp inhibitor. Here we provide a brief description of the models and the inferred molecular characteristics. The molecular descriptors employed in these models have been described in Supporting Information II.
| Model | Descriptors supplied | Descriptors incorporated manually | Group | Risk Estimate | Standard Error (±) |
|---|---|---|---|---|---|
| RT | All descriptors | - | Train | 0.428 | 0.044 |
| Test | 0.856 | 0.197 | |||
| CHAID | All descriptors | - | Train | 0.559 | 0.069 |
| Test | 0.682 | 0.188 | |||
| I-tree | All descriptors | Docking energies | Train | 0.66 | 0.079 |
| Test | 0.556 | 0.105 | |||
| BT | All descriptors | - | Train | 0.162 | 0.016 |
| Test | 0.563 | 0.15 | |||
| RF | All descriptors | - | Train | 0.419 | 0.049 |
| Test | 0.563 | 0.121 | |||
| MARS | Selected descriptors | - | Train | - | 0.051 |
| Test | - | 0.133 |
Table 1: Standard error for the training and internal test sets for the selected models.
Regression trees
Figures 1 and 2 show the regression trees obtained using CART and CHAID, respectively. In the regression trees, N is the number of P-gp inhibitors, Mu is the average, Var is the variance of log Ki in each node, and ID is node number we have referred to in the text (e.g., ID=3 is node 3). Also note that terminal nodes (i.e., leaves) have been shown in red boxes, while non-terminal nodes are in blue boxes. It can be seen in Figure 1, that the molecular descriptor selected by CART algorithm for the first split of the data is SlogP (octanol/water partition coefficient). The tree indicates that compounds with lower lipophilicity than SlogP=3.179 are less potent inhibitors of P-gp and, with average log Ki of 1.88 (node 2), they may be considered as non-inhibitors. On the other hand, potent inhibitors are very lipophilic (node 3), and highly lipophilic compounds with a higher number of aromatic bonds are generally considered as strong inhibitors (node 5), particularly those with no five-membered rings in their structure (node 8). Besides, within the high lipophilicity compounds (SlogP>3.179) those with lower number of aromatic bonds have an intermediate inhibitory activity (node 4) that will be increased based on the presence of atoms with LogP(o/w) contribution of 0.15-0.20 (SlogP_VSA5) in their structures (node 7). Numerous atoms of these types have been presented by Wildman and Crippen [56]. Further splitting in this tree indicates the effect of very large polar surface area (vsa_pol>43.3), which will significantly decrease inhibitor potencies (node 11).
Figure 2 is the selected model developed by CHAID method. Similar to the CART result, SlogP is the first (most important) descriptor in this CHAID model. In this case compounds have been split into five branches, two of which are terminal nodes. According to this first level of data partitioning, there seems to be an optimum level of lipophilicity for the maximum inhibitory potency at the SlogP range within 4.852 < SlogP ≤ 6.852. This is in agreement with previous studies that have described LogP as an important parameter in drug binding to P-gp [20,37,57]. The significance of LogP in P-gp inhibition is due to the presence of several lipophilic and aromatic residues in the binding sites of P-gp [19]. With the exception of a few compounds in node 10, compounds with lower lipophilicity (SlogP < 4.852) are generally poor inhibitors of P-gp. Compounds in node 10 are those with 2.264 < SlogP ≤ 3.874, which have been tested using probe substrates that are moderately ionized (fraction unionized (S-fU) of between 0.000 and 0.240 at pH 7.4 for the substrate). Compounds with lipophilicity in the range 3.874 < SlogP ≤ 4.852 have an average log Ki of 0.89, which will be lower (more potent) if the compounds have large negative surface area (composed of atoms with PEOE atomic charge below -0.30) (node 13 with PEOE_VSA-6 > 7.767).
Relatively hydrophilic compounds with SlogP ≤ 2.264 (node 2) have been partitioned based on their number of double bonds where those compounds with three or less double bonds are much weaker p-gp inhibitors (compare node 7 and 8), especially those in node 14 that have 8 or fewer rotatable bonds (opr_nrot).
Significance of P-gp docking energies
Despite using P-gp/inhibitor interaction energies from docking studies as one of the molecular descriptors, none of the decision tree algorithms above picked docking scores for partitioning of the log Ki data. This was explored further by using the docking scores in interactive tree (I-tree) model (Figure 3). Docking score was incorporated as the first variable for partitioning of the data and this was found statistically significant by cross validation. Figure 3 shows that the statistically selected threshold for docking energy is -13.140 (kcal/mol). Compounds with docking energy below this value (node 2) are more effective inhibitors than those with higher docking scores especially if they contain a large hydrophobic volume at the highest hydrophobic interaction level (77.062 ≤ vsurf_D8) (61 compounds in node 5). However, this tree is not successful in identifying the very strong inhibitors (top 25% with average log Ki of -0.128), and all the terminal nodes of the tree have a moderate log Ki . More specifically, Figure 1 has a terminal node with average log Ki of -0.85 and another with the average log Ki of 0.09, while the minimum log Ki in Figure 3 is 0.43 (node 5).
Docking is a very useful tool in computer-aided drug discovery due to the importance of shape-matching in drug-macromolecule interactions, as well as the properties of contact surface between the drug and the protein. It has been postulated that compounds with shape and chemistry similar to those of a known active molecule have a high probability of being active [58]. On the other hand, the interaction energy can be notoriously misleading with large molecular weight compounds often achieving the most negative interaction energies due to the additive nature of the energy formula [59-60]. In our training set, the top ten molecules with the most negative interaction energies had an average molecular weight of 925 Da in comparison with an average of 461 Da for the remaining compounds in the training set. On the other hand, these ten compounds had a lower average log Ki of 0.71 in comparison with 1.26 for the remaining compounds in the training set.
In addition, docking experiments are most reliable when interaction between a rigid protein target and a flexible ligand is investigated [61]. For docking results to successfully guide the predictions of inhibitors and substrates of P-gp, it should take into account the very flexible nature of this enzyme [62]. Previous studies have described the importance of protein flexibility in P-gp ligand interactions [63,64]. Induced fit mechanism explains the fact that both drug and protein are flexible, and can modify their shape to generate more favourable contacts [65]. Current evidence shows that P-gp is able to accommodate a wide range of substrates due to the mobile nature of its transmembrane helices [63,66]. However, docking algorithms have limitations in predicting large conformational changes that are common for some proteins up on binding with the ligands.
Ensemble decision trees
Studies have shown that an ensemble of several trees may result in better prediction accuracy when there is a significant diversity among the models [67]. In this investigation BT and RF were used. BT method is an ensemble method that computes a sequence of simple trees, each built for the prediction of residuals of the preceding tree. Various combinations of subsample proportions and learning rates were examined and the best model was selected based on the prediction error for the test set. The best result was obtained with the subsample of 0.6 and learning rate of 0.05, using the optimum number of trees of 161 (Supporting Information III, Supplementary Figure S1).
The top ten most important descriptors as calculated by STATISTICA software has been described in Supporting Information II. Different orders of molecular connectivity indexes (three descriptors), number of carbon atoms, categorical variable indicating the nature of the substrate, lipophilicity, hydrophilic volume, polar volume, and molecular polarizabilities were the most important BT descriptors.
RF is another ensemble method; it develops a number of decision trees using a random selection of training set compounds and molecular descriptors. The graph of average squared error against number of trees for training and cross-validated test sets indicated that the test error reaches a plateau at around 60-70 trees (Supporting Information III, Supplementary Figure S2).
In this selected RF model, molecular features that indicate surface lipophilicity/hydrophilicy were the most important model features. These included volsurf descriptors indicating ratio of hydrophilic volume, total hydrophobic volume, and hydrophilic/lipophilic balance, lipophilicity parameters (partition coefficient and distribution coefficient), hydrophobic surface area and number of aromatic bonds. In addition VDistEq, an adjacency and distance matrix descriptor that is a highly discriminating topological index representing the extended connectivity and the shape of molecules [68] has been selected as one of the top 10 most significant descriptors of the model.
MARS model
Many combinations of molecular descriptors picked by several preprocessing feature selection methods were used in MARS analysis to obtain the best possible model. The feature selection methods included Chi-square method, stepwise regression analysis, and variable importance rank from RF and BT analyses. Previous investigations have shown that predictor importance using RF is a very successful feature selection method that can be applied for reducing the data dimensionality prior to CART analysis [69]. Here, the best MARS model was obtained using 12 descriptors from STATISTICA feature selection and variable screening as the independent variables. Subsequently, as a result of the pruning function in MARS analysis, four out of the 12 molecular descriptors were used in the selected model (presented in Table 2). The MARS model in Table 2 consists of nine basis functions with two descriptors employed in three basis functions each; one descriptor employed in two basis functions and one remaining descriptor is involved in one basis function. This model does not contain any interaction terms. The descriptors of this model are not highly correlated, with the highest intercorrelation showing a Pearson correlation coefficient of -0.70. In this model, molecular descriptors have been presented according to the rank order of their importance, with the most important descriptor being the first one in the equation.
| LogKi = 4.199+ 1.87*max(0, SlogP-6.119)– 0.46*max(0, 6.119-SlogP) – 0.82*max(0, chi1v_C-13.115) + 0.76*max(0, chi1v_C-10.310) – 0.80*max(0, SlogP-1.785) + 0.56*max(0, LogD(10)-2.790) + 0.42*max(0, opr_leadlike-0.000) – 0.23*max(0, chi1v_C-8.114) – 0.43*max(0, LogD(10)-0.820) | |||
| N=176 | GCV error=0.633 | Mean residual=0.000 | SD(residual)=0.712 |
Table 2: The selected MARS model.
An interesting feature of the MARS model is the knots at 1.785 and 6.119 for octanol/water partition coefficient, SlogP; these show that increasing the lipophilicity of the inhibitors from 1.785 to 6.119 leads to a reduction in log Ki values i.e., stronger inhibitors. On the other hand, for compounds with extremely high or extremely low lipophilicity (SlogP > 6.119 or SlogP < 1.785) with increasing lipophilicity an increased log Ki values will be observed. In addition to this, distribution coefficient at pH 10 (LogD(10)) is also used in the model; it indicates increase in potency of inhibitors when LogD(10) increases from 0.82 to 2.79, but increase in LogD(10) above 2.79 results in the reduction of inhibitory potency. It must be noted that LogD(10) is a lipophilicity parameter that is also affected by acid/base property of compounds, and it is higher for basic compounds while lower for acidic compounds. The next descriptor of the MARS model is carbon valence connectivity index (a topology descriptor) with three knots at 13.115, 10.310 and 8.114. The model indicates that increasing the connectivity index results generally in increased potency (reducing Ki values) with the exception of compounds with 10.115 < chi1v_C > 13.115 where the relationship is opposite.
Finally, lead-like descriptor (opr_leadlike) in the model indicates that compounds with non-lead-like molecules (according to Oprea’s definition [70]) have strong inhibitory activity towards P-gp. This observation regarding the higher inhibitory activity of non-lead-like compounds is in agreement with a recent study by Wang et al., in which lead-like compounds had lower propensity to be P-gp substrates [71].
Validation of models
All models were validated using an external validation set of 43 compounds. Table 3 shows the error of the selected models for the prediction of log Ki values of the training set and external validation set. It can be seen that the chi-square based decision tree model (CHAID model) gives the most accurate prediction of log Ki for the validation followed by BT and RF. For the training set, BT calculates the most accurate log Ki values followed by CHAID and the RF model. The difference between model accuracy for training and validation sets may indicate the possibility of overfitting into training data. In this case, amongst the top three models listed above for the validation set prediction accuracy, CHAID has the lowest difference between the training and the validation set errors, while RF has the greatest difference.
| Model | MAE* for training set | MAE for validation set |
|---|---|---|
| RT | 0.519 | 0.707 |
| CHAID | 0.399 | 0.511 |
| I-tree | 0.626 | 0.607 |
| BT | 0.322 | 0.554 |
| RF | 0.488 | 0.601 |
| MARS | 0.589 | 0.651 |
Table 3: The summary of the prediction accuracy of the Ki values. *MAE is mean absolute error.
Effect of substrates on the Ki measured for the inhibitors
It has been suggested that there are several binding sites for the molecularly diverse spectrum of P-gp substrates, inhibitors and modulators. For example, using equilibrium and kinetic radioligand binding assays, Martin and co-workers established the presence of at least four distinct interaction sites on P-gp which were able to communicate allosterically [21]. Moreover, various competitive, cooperative allosteric and anticooperative allosteric interactions are possible between the substrates and regulators [20]. As a result, the inhibitory activity measured using different substrates will be different for the same inhibitor [42]. The x-ray structure of mouse P-gp with 87% sequence identity to human P-gp has recently been described [19].
It was found that P-gp can distinguish between different 3D shapes, and that stereoisomers may bind to different binding locations. Given the complexity of the binding locations and modes of inhibition, it has been suggested that a single pharmacophore cannot effectively describe the inhibitors of various P-gp substrates and, therefore, different pharmacophores have been proposed for the inhibition of the transport of different P-gp substrates [72]. The modelling strategy described in this study should be able to deal with the diversity of the binding sites. In particular, molecular descriptors of the substrates were incorporated in the model development in addition to molecular descriptors of inhibitors.
Regression tree is a powerful data mining tool that is able to select the important features for dividing the data into high or low activity groups (distinct groups of compounds with high or low average log Ki values). The models described above indicate the importance of substrate in the measured inhibitory activity as, the two most accurate models, BT and CHAID models, contain substrate descriptor selected by the feature selection methods.
Structural determinants of potent P-gp inhibitors
Inhibitors of P-gp can be competitive inhibitors that may bind to the substrate binding site, or non-competitive which may bind to other distinct binding sites such as the ATP-binding site. An investigation that involved docking of multispecific inhibitors into the ATP-binding domain of P-gp has shown that some of the less lipophilic inhibitors can bind to this site, which may contribute to their inhibitory activity [37]. On the other hand, the more common, lipophilic inhibitors do not interact with the ATP-binding domain of P-gp. Inhibitors from the steroid and flavonoid chemotypes are examples that may bind to the ATP-binding site [73,74]. The training set in this study did not contain any flavonoids but included five steroids (testosterone, progesterone, spironolactone, digoxin and cortisol). These steroids are also expected to bind to the substrate binding site. For example, studies for several sex-steroid hormones have shown that they are substrates of P-gp mediated transport as well as being a P-gp enzyme inducer [75]. Another example is digoxin with a steroid structure that is also a known substrate of P-gp as well as acting as an inhibitor [76].
From the description of the models outlined above, it can be seen that lipophilicity is the key factor for P-gp inhibition along with the molecular topology and the size of the inhibitors as well as the nature of the substrate probe. In terms of the lipophilicity, a higher partition coefficient than what is recommended for drug-like molecules (based on Lipinski or Oprea’s rules) improves the inhibitory activity towards P-gp. According to the best model (CHAID), the ideal lipophilicity is SlogP value in the range (3.874,6.852). A similar pattern can be observed in MARS model where SlogP increase from 1.785 to 6.119 increases the inhibitory potency. Previous studies using classification models have found a higher lipophilicity (log P) for multispecific inhibitors of P-gp in comparison with non-inhibitors [37,74], although these studies have not specified a maximum lipophilicity threshold. For P-gp substrates also a higher lipophilicity requirement has been reported in an investigation using a large set of proprietary GSK compounds (i.e., a log P>4 for the substrate class) [77].
Apart from the partition coefficient, other lipophilicity measures, which also indicate the size of the lipophilic regions, are found to have an impact. Hydrophobic volumes measured by volsurf parameters (vsurf_D1, vsurf_D2, vsurf_D6 and vsurf_D8) are among the top 10 most important parameters of the BT and RF models and a large vsurf_D8 indicates higher inhibitory potency in the I-tree model, while a small Polar van der Waals surface area (vsa_pol) in RT model improves potency of the inhibitors. These parameters are indicators of both size and lipophilicity. The positive impact of large molecular size and lipophilicity is in agreement with the known structure of P-gp and its proposed substrate binding pocket, where the large binding site of P-gp consists of a considerable number of lipophilic amino acids [2]. The surface area as a descriptor has also been used by Demel and colleagues for the classification of substrates/nonsubstrates, which indicates compounds with hydrophobic surface area>300, log P<7 and more than seven hydrogen bond acceptor groups are substrates of P-gp [78]. Lipophilicity and molecular size have also been indicated in local QSAR models for individual classes of modulators/ substrates [57].
Higher inhibitory activity of non-lead-like compounds (based on Oprea’s definition) in the MARS model may indicate the positive effect of large molecular size and higher lipophilicity than lead-like molecules. Compounds that accommodate the Opera’s test are defined as compounds with molecular weight ≤ 460 Da, -4 ≤ Log P ≤ 4.2, Log Sw ≥ -5, number of rotatable bonds ≤ 10, number of rings ≤ 4, number of hydrogen donors ≤ 5 and number of hydrogen acceptors ≤ 9 [70]. According to our models, compounds that violate more than two of the above rules are better inhibitors of P-gp. A close observation of such compounds indicates higher lipophilicity, as well as higher molecular size and number of rings are the reason for the violations that results in compounds considered to be inhibitors. Examples are paclitaxel, nicardipine and vinblastine.
Other significant molecular determinants of P-gp inhibitors are the molecular topology and shape as described by the adjacency and distance matrix descriptors, such as the Kier and Hall molecular connectivity index (chi0_C, chi0v_C and chi1v_C) in the BT and MARS models, number of rings in the RT model and VDistMa in the RF model. Broccatelli and co-workers [74] have hypothesised that an optimal shape may exist for P-gp inhibitors, but the optimal shape needs to have adequate lipophilicity and H-bond acceptor ability. Hbond acceptor ability has also been emphasised by Demel et al. [78] which show the importance of a high number or a large surface area of H-bond acceptor groups. In the models presented in this study, the effect of H-bonding is seen in the top 30 RT and RF models, including negative charge weighted surface area (CASA-) and partial charge descriptors [79]. It must be noted that these parameters as well as the H-bonding parameters of Demel et al. may also relate to the molecular size as larger molecules are more likely to contain many H-bond groups.
It is worth mentioning that the most accurate model in this study, i.e., CHAID model relies heavily on the lipophilicity of compounds as there are only four additional molecular descriptors in the tree to further adjust the predictions based on other molecular properties. Outliers of this model clearly indicate that more specific structural characteristics of the molecules are involved in their binding and inhibition of P-gp. For example, there are five outlier compounds with an absolute log Ki error of >1.6. Of these outliers, dipyridamole and loperamide were both overpredicted, while montelukast, paroxetine and verapamil (when digoxin or irinotecan were the probe substrates) were underpredicted. All of these outliers, except paroxetine, have very large (five times larger than the average of all compounds) van der Waals surface area of minimally charged (mainly carbon) atoms identified by SlogP_VSA2. This shows a large SlogP may be misleading in the prediction of log Ki when other structural characteristics are also involved.
The Best model (CHAID) showed a similar MAE for the compounds with or without Lipinski’s rule of five violations and Oprea’s lead like violations (MAE values ranging from 0.393-0.411, differences not significant with P > 0.05). The range of descriptors used in the CHAID model for the training set were SlogP within -1.651 to 7.889, b_double within 0-5, S-fU within 3.753E-8 to 0.999, PEOE_VSA-6 within 0.136-25.687 and opr_nrot within 0 to 25. It is expected that any test set data within these descriptor ranges will perform well with an MAE of 0.399.
In order to develop accurate models for the P-gp inhibition, this study used Ki values of large set of P-gp inhibitors calculated from the reported IC50 and the probe substrate’s Km and concentration values from the literature using Cheng and Prusoff’s equation. In comparison with IC50, this parameter allows a better comparison between inhibitory activities measured using different probe substrates and substrate concentrations. In addition to the molecular descriptors of the inhibitors, this QSAR study also incorporated the molecular descriptors calculated for the probe substrates as the nature of the substrate used in the experimental measurement of IC50 or Ki may affect the inhibitory activity of the inhibitor.
The study resulted in a few predictive models based on the accuracy of the prediction for the external validation set. The results indicated that substrate parameters were important for the prediction of the inhibitory activity as the top two best models incorporated substrate molecular descriptors in addition to the molecular descriptors of the inhibitors as selected by their feature selection procedures. In this study docking scores were not found to be good predictors of inhibitory activity, as they were not selected by any of the feature selection methods described here. However, when these docking scores were incorporated manually in CART analysis, docking scores were statistically significant in the regression tree model (I-tree) with an average prediction error for the validation set. The most significant models indicated a higher lipophilicity of the potent inhibitors than lead-like compounds. The potent inhibitors contained a high molecular weight, a high volume of hydrophobic groups and a large surface area.
The best model was based on a chi-squared based regression tree; CHAID followed by the BT model the RF models. The statistical parameters of the CHAID and the RF models indicate that they have a lower chance of overfitting in comparison to the BT model. Models indicated that the potent P-gp inhibitors have higher lipophilicity and molecular weights than drug-like molecules identified by Oprea's rule.
Authors gratefully acknowledge the NIH Fellows Editorial Board for constructive comments, careful review and correction of the manuscript, support and assistance for this work. M. Sharifi would like to thank Jon Wilkes at NCTR for his assistance and also would like to thank Natalia Aniceto at Medway School of Pharmacy for helping with recalculation of molecular descriptors.
Supporting Information associated with this article can be found in the online version. These data include the dataset containing Ki values (Supporting Information I), molecular descriptors employed in the models (Supporting Information II), graphs of average squared error against number of trees for BT and RF models (Supporting Information III).
The authors declare no conflict of interest. The views presented in this article are those of the authors and do not necessarily reflect those of the US Food and Drug Administration. No official endorsement is intended nor should be inferred.