The life cycle of intra organelle naonpores depends on the organelle membrane elasticity which is numerically the function of surface tension, pressure and characterized by rest potential or in the form of pore current as reported by Kotnik et al., Pakhomov et al. and Ferrier et al. [1-3] shows that these parameters have a remarkable effect on life cycle of pores and they have direct influences on the nanopore formation into the intraorganelle membrane of a rigid bone cell like osteoblast. A numbers of experimental study carried on at the outside of the micro fluidic but all the reported studies on cell membrane surface tension, pressure and pore current considered the cells in an infinitely large medium. In micro fluidic devices, the cells are usually located in micro channels or micro chambers. The results of the current published studies may not reflect the boundary effects of micro fluid-based electroporative devices. It should be focus out that all the reported studies on cell membrane surface tension considered the cells contained single layer placed in an infinitely large medium and electrodes are placed at bottom or top layer of the micro fluidic devices. As a result the results are influenced by reflect the boundary effects of micro fluid-based electroporative devices and perfect optimization is to be needed. As a result the original and realistic information about the surface tension of outer and inner membrane is limited for multi layer or bi layer cell mainly in rigid cell like bone cell. Hartig U et al. [4] vstate that as per the morphological structure the osteoblast cell is more rigid than other biological cell. This structure gives a challenge to the scientist for its intra organelle pore current characterizations. The current doctoral research we mainly focus on the above limitations and investigate the membrane surface tension, pressure and pore current of a bi-layer osteoblast cell located in a non uniform micro fludic system. In this context the pulse shape was chosen as a square wave, which is widely used in the micro fluidic devices. This electric pulse shape can be easily generated by contracting the cross-sectional area of the micro channels or using a high-voltage pulse generator.

In this analysis we consider the process of membrane rupture or pore formation into the intraorganelle of rigid cell like Osteoblast. There have been several theoretical models developed to describe Bi-Layer Membrane (BLM) stability and breakdown at an elevated transmembrane potential and the key elements are reviewed. Hall et al. was first suggested that the compression of the entire membrane by the electric field might cause mechanical collapse leading to membrane rupture. In this approach, the BLM is treated as an elastic capacitor with a constant elasticity of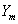. The pressure on the membrane due to the electric field is given by 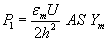is a constant, So the elastic forces per unit area, P_m is given by 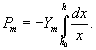Where h₀ is the membrane thickness when applied voltage is zero. Beebe et al. [5], state that for electromechanical equilibrium, P₁=P_m, gives an equilibrium thickness value of h, which is a function of the transmembrane voltage (U). However, when U is larger than a critical value, 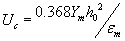there is no root for the equation. Roland Winter et al predicts that breakdown takes place when the trans-membrane voltage exceeds this critical voltage U_c, which is too large. This model also suggests that a trans-membrane voltage less than U_c does not lead to electric breakdown, whereas experiments have shown that rupture is a stochastic process with higher probability at higher trans- membrane and longer pulse durations. Crowley et al. [6] shows that an alternative approach to the rupture of a BLM, to the creation of pores, considers the electro hydrodynamic instability of a bi-layer membrane. In this study we find out the effect of membrane pressure on intraorganelle nanoporation which is characterized by pore energy and pore density as well as pore radius.

Weaver et al. [7] explores the internal structure of intra organelle bilayer membrane is moderately elastic and most of the time it is respond through a squeezing mode, that will be damped due to the large elasticity of membrane compression and the constant volume constraint that applies to the membrane. According to Montal Mueller et al. [8] model, the membrane is unstable with respect to long-wave perturbations if 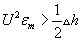.For Γ = 10^-3 J m^-2, U_c = 0.375 V in reasonable agreement with the experimental results. According to electro-compression model, the threshold voltage for breakdown is 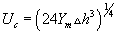. Again, this model fails to describe the stochastic nature of membrane rupture, and the strong dependence of the membrane lifetime on the transmembrane voltage (U). The surface tension can be expressed by the integral of the normal pressure 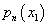and tangential pressure pn (x₁) along the (field) direction denoted by coordinate (x₁). So the surface tension is numerically defined as 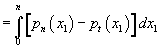The external electric field, by generating additional stresses T1, T2 and T3 changes the membrane surface tension to 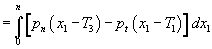. The overall change in surface tension is 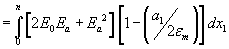. Where E₀ is the natural resting field of the cell membrane and E_a the additional field, a₁denotes the strain in the membrane in thex₁ direction. From this relation it is come to know that for large values of E_a, stress is always negative and the field may therefore reduce the membrane surface tension to zero, resulting in the total loss of cohesion of the phospholipid molecules and rupture the bi-layer membrane. This rearrangement may cause the formation of pore into the intraorganelle membrane. In this analytical and theoretical study we explore the role of surface tension on pore energy, pore density and radius that elucide the property of intraorganelle nanoporation.

Peter Tieleman et al. state the Laplace’s equation, that can be used to measure the intracellular and extracellular transembrane potential denoted as 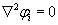for intracellular and 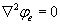extracelluler potential. The current density across the membrane S is given by 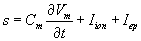.Where C_m is the specific membrane capacitance, v_m is the transmembrane potential on the membrane, t is time, I_ion is the ionic current, and I_ep is the current due to electroporation. To focus on the effects of electroporation, the cell is assumed to have passive membrane kinetics in which I_ion can be described as 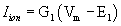, where G₁ is the specific membrane conductance and E₁ is the rest potential of the ionic current. As the rest potential is the sole component of current density so it has great influences on free energy, density and radius of intraorganelle nanopores. In this current doctoral research we investigate the role of rest potential on intraorganelle nanoporation

In this research papers we analytically explain the dependency of pressure, surface tension and rest potential on free energy of pores as well as density and radius of nano pores, which produces within the intra organelle.

In theoretical and numerical study, we assume the bi-layer model of the system shown in Figure 1, which is used to investigate the change of membrane surface tension, electrostatic pressure and pore current by applying external electric field in an non uniform micro channel at radio frequency. In current research the bi-layer model of the cell located in the micro chip to study the effects of various boundary conditions, including the pulse, micro electrode micro channel dimensions and basic property on intra organelle pore current, pressure and surface tension.

Figure 1: Schematic of Multi Layer Spherical Cell in Suspension

Intra organelle voltages, current, pressure and surface tension

Yao [9] gave the following Schematic diagram of double-shelled spherical cell in suspension, which is used for theoretical explanation of outer and inner membrane potential of a biological cell.

After simplification of equation we get the outer membrane potential 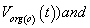inner membrane potential are as 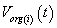follows

--(1)

--(2)

The following Schematic diagram of double -shelled spherical cell in suspension, which is used for theoretical explanation of outer and inner membrane potential of a biological cell. According to the transfer functions defined by Yao, Saeid Movahed, Dongqing [9,10] the inner and outer membranes of intraorganelle to a given rectangular pulse electric field E(s) , that the pore current are expressed respectively,

--(3)

--(4)

--(5)

Where

I_epo= Outer membrane intraorganelle pore current.

I_epi = innermembrane intraorganelle pore current.

V_n(i)(t) = Intraorganelle Inner membrane potential.

V_n(o)(t) = Intraorganelle Outermembrane Potential.

If we replace the value of V_n(o)(t) and V_n(i)(t) in equation (1) and (2) than established the relation among the pore current with pulse specification.

It is reported in that when electric field is applied on a biological cell specific pressure is inserted into the intraorganelle, which is mathematically expressed as

--(6)

--(7)

Where P_o and P_i are the outer and inner membrane intraorganelle pore current, εm and εn are the permittivity of the outer and inner membrane, h shows the thickness membrane and “F” accounts for applied force on membrane. So the surface tension also changes in both layers, which is mathematically expressed as intraorganelle Surface tension for outer membrane.

--(8)

Where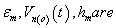 permittivities, thickness, potential of the outer membrane respectively, If we put the value of from the equation 2.26 in equation (6) we get,

--(9)

Whereas the innermembrane surface tension of intraorganelle is calculated as

--(10)

Where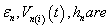permittivity, potential, thickness, of the intraorganelle, than if put the value of from the equation in equation (8) we get,

Radius of nanopores

Based on the theory of membrane permeabilization, given by Weaver et al. [7] , the nano pores are initially created with a radius of r*. By increasing the applied electric field, nano pores start to develop in order to minimize the energy of the cell membrane. For the intra organelle with nanopores, the rate of change of their radius of pore (r) can be determined by the following set of equations.

--(11)

Where D is the diffusion co efficient,K = boltz man constant, T= absolute temp, 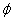(r,θ ) = intra organelle potential. γ = Surface tension

Intra organelle pore density

DeBruin and Krassowska [11] exposed that the rate of creation of nanopores at intra organelle can be found as

--(12)

Where N(t) is the pore density.

Intra organelle ion uptake

It is known from the bio chemistry that the ion uptake can be calculated by following mathematical calculation

--(13)

D = Diffusion of Co efficient

V_c = Area of pore

d = thickness, Sc = N.π.r²

T = Temp in kelvin. Kb=Boltz man constant.ε w = permitivity of water, εc = permitivity of cytoplasm. te = pulse duration. r1= radius of pore, r = radius of initial pores, V_org(i) (t) =intra organelle potential.

Numerical simulation

In this study, above Equations are solved numerically to find the each and every parameters of nanoporation to investigate the creation of nano-pores on the cell membrane. The Mat lab 7.2 & Comsol-4.3a, commercial package was used in the numerical simulations. In order to discrete the solution domain, unstructured meshes were applied. The solution domain was broken into small meshes to allow meshes to fully cover the solution domain without overlapping.

Electric field strength analysis

Figure 2 depicts the potential distribution with the proposed 3D micro chip where we find the non uniform distribution of potential and intra cellular organelle also effect by this field. At pole θ = 90° and θ = 270° the maximum potential are exposed which is similar as our numerical result. Figure 3 complete electrical potential distribution within the 3D hybrid micro chip. All the information exposed in COMSOL simulation is as similar as numerical and experimental values of intra organelle nano poration of multi layer dense osteoblast cell.

Figure 2: Electrical field gradient within the 3D hybrid micro electrode

Figure 3: complete electrical potential distribution within the 3D hybrid micro chip

Design layout

It is reported that the effective nanoporation in intraorganelle membrane or nucleous membrane need specific type of pulse, microfloudic chip and suspension media. The optimum value of the applied pulse having the duration of 5 peco second, pulse intensity of 1 volt is suitable and effective intraorganelle nanoporation of osteoblast cell. it also exposed that intraorganelle nanoporation can easily obtained if the shape of the electrode is triangular or saw tooth which are made by gold bismuth alloy in specified micro channel having the height and width of micro -fluidic channel should be moderate and same and it would be taken as 200 micrometer for successful and effective intraorganelle nanoporation. The resistances of micro channel should be as high as possible for above purpose. We optimised the system and designs a simulating micro fluidic chip on the bases of following specification with in which the osteoblast cell is placed, to explore the numerical and analytical characterization of intraorganelle nanoporation. The simulation tool is composed of a 100 μm thick SU8 micro fluidic channel including thick bi metallic electrode (Bi and Au) electrodes with a typical thickness of 50 μm, in which cells suspended in a biological medium are injected. Bi-metallic is chosen as material for the electrodes because of its excellent electrical properties and bio compatibility. The biochip is designed in such a way that the pulsed electric field is absorbed and dissipated mainly in the biological medium placed between the electrodes within which cells to be treated are flowed.

Figures 4-6 shows the top view of nanoporative devices. This numerical model satisfy the all simulating and analytical values of intra organelle nanoporation. Length, Height & Width of the microchip are 2300, 100, 900 μm respectvely. The inlet and outlet path are same i.e 10 μm. Within the micro chip a non uniform sidewall having the mixed dimension micro-electrode is places which is made by bismuth and gold

Figure 4: Dimension and design of microelectrode and micro channel within the 3D hybrid micro chip (Top view)

Figure 5 represents the sidewall micro electrode reside the micro chip. The shape of this electrode is the combination of three different shaped electrodes. The central part consists of triangular, medial part consists semicircle and terminal part attached with square shaped electrode. The length, width and height of the micro electrode are 1000, 900, 100 μm, as the electrode is hybrid in nature so inter electrode gap is non uniform throughout the whole micro channel. The inter electrode distances of central, medial and lateral part are 50, 150, 250 μm respectively.

Figure 5: Dimension and design of microelectrode placed within the 3D hybrid micro chip

Figure 6 explores that complete design of 3D hybrid micro chip; contain microelectrode, micro channel and their combination. The micro channel is specified by Length, Width, Height and their dimention are 2300, 250, 100 μm.

Figure 6: Dimension and design of complete 3D hybrid micro chip

Effect of pressure

Free energy of pore: The Figure 7 shows that free energy pore is gradually decrease with the increase of radius of the pore for hydrophilic pore (a) until the nanopores are formed. After the formation of nanopores pore energy starts to increase but after a certain limit energy is constant due to the sustainibility of pores. But variation of energy does not depends on the pressure of membrane. It only depens life cycle of the pores.In case of hydrophobic pores (b) the pore energy is expotentially increase with the increase of radius but independent of pressure.

Figure 7: Variation of free energy with radius for (a) hydrophilic pore (b) hydrophobic pore in different pressure of membrane

Density of pores: The Figure 8 shows the variation of pore density with the change in angle of applied electric field for (a) outermembrane and (b) innermembrane in different pressure. On the basis of polar location, the outer membrane pore density is non uniform but independent of pressure.In case of innermembrane pore density is nonuniformly distributed. The maximum pores are exposed at theta (θ) = 100° and value of pore density is direcly proportional with the electrostatic pressure of membrane.

Figure 8: Variation of pore density with change in angle of applied electric pulse a) outermembrane (b) Inner membrane in different pressure

Effect of pressure on pore density and pore radius: Figure 9 reflects the variation of (a) pore density and (b) pore radius with different pressure. The pore density is linearly increased whereas pore radius is exponentially increase with the change of membrane pressure due to the different elestic property of the membrane.

Figure 9: Variation of (a) Pore density (b) Pore radius with change in different pressure

Effect of surface tension

Free energy of pore: The Figure 10 shows that free energy pore is gradually decrease with the increase of radius of the pore for hydrophilic pore (a) until the nanopores are formed. After the formation of nanopores pore energy starts to increase and variation of energy depends on the surface tension of membrane. But in case of hydrophobic pores (b) the pore energy is expotentially increase with the increase of radius but independent of surface tension.This observation conclude that the formation of pores in the membrane considers the energy balance in the membrane, which, undisturbed, has an energy per unit area, when a circular pore is created, there is an energy gain from the creation of a circular rim under strain denoted by surface tension but there is also a reduction in energy due to the loss of the discshaped cut-out in the membrane surface of the osteointraorganelle.

Figure 10: Variation of free energy with radius for (a) hydrophilic pore (b) hydrophobic pore in different surface tension of membrane

Radius of nanopores: The Figure 11 shows the variation of pore radius with the change in angle of applied electric field for (a) outermembrane and (b) innermembrane in different surface tension. For same electric field, the different size of nanopores are appears on the both layer and they are nonuniformly distributed. The biggest nano pore is situated at theta (θ) = 90° and value of pore radius is direcly proportional with the surface tension of the membrane. As per the numerical value radius of outer membrane pore bigger than inner membrane in same surface tension and electric field due to different elastic property of the membrane.

Figure 11: Variation of radius of pores with change in angle of applied electric pulse (a) outermembrane (b) Inner membrane in different pressure

Density of pores: The Figure 12 shows the variation of pore density with the change in angle of applied electric field for (a) outermembrane and (b) innermembrane in different surface tension. On the basis of polar location, the pore density is non uniformly distributed but independent of surface tension in outer and inner membrane. The maximum pore density is obtained at theta (θ) = 100° and it is uneffected by surface tension.

Figure 12: Variation of pore density with change in angle of applied electric pulse (a) outermembrane (b)Inner membrane in different pressure

Effect of surface tension on pore density and pore radius: Figure 13 reflects the variation of (a) pore density and (b) pore radius with different surface tension.The pore density is linearly increased whereas pore radius is exponentially increase with the change of surface tension of the membrane.Although in polar position there is non effect on pore density but in numerical value the pore density is effected by surface tension. This result concludes that the Bi-Layer Membrane act as a metastable system, in which the surface tension (energy per unit area) of the membrane is positive. Thus, broken membranes have lower free energy than intact membranes. Nanoporation is then considered as the nucleation of a new phase (a membrane containing pores) from the intact state, in the presence of a pulse electric field.

Figure 13: Variation of (a) Pore density (b) Pore radius with change in different surface tension.

Effect of rest potential

Free energy of pore: Figure 14 shows the variation of pore energy with radius of pore presences (a) and absences (b) of rest potential. But there is no remarkable observation regarding the effect of rest potential on pore energy.

Figure 14: Variation of free energy of pore with radius (a) Without rest potential (b) With rest potential

Radius of nanopores: The Figure 15 shows the variation of pore radius with the change in angle of applied electric field for (a) outermembrane and (b) innermembrane for presents and absences of rest potential. For same electric field,the different size of nanopores are appears on the both layer and they are nonuniformly distributed .The biggest nano pore is situated at theta (θ) = 100° and value of pore radius is inversely proportional with the rest potential. As per the numerical value radius of outer membrane pore bigger than inner membrane due to different elastic property of the membrane.

Figure 15: Variation of radius of pores with change in angle of applied electric pulse (a) outermembrane (b) Inner membrane for the effect of rest potential

Density of pores: The Figure 16 shows the variation of pore density with the change in angle of applied electric field for (a) outermembrane and (b) innermembrane for presents and absences of rest potential. The pore density is non uniformly distributed and maximum pore density is obtained at theta (θ) = 100° for both layer and value of pore density is inversely proportional with the rest potential. As per the numerical value pore density of outer membrane is greater than inner membrane due to different elastic property of the membrane.

Figure 16: Variation of pore density with change in angle of applied electric pulse (a) outermembrane (b) Inner membrane for the effect of rest potential

due to different elastic property of the membrane. The numerical values of pore density and pore radius with or without presences of rest potential are shown are shown in Table 1.

The intrinsic rest Potential (V_rest) of the cell will alter the pore density (N) and radius (r) profile by shifting it in the direction of V_rest N and r at the poles would still be symmetric about the equator, but they are at that location would be equal to the rest potential. However, in this scenario, the transmembrane potentials still far exceed the critical potential for electroporation, so significant electroporation will occur at both ends of the cell. Intuitively, one would expect that the negative bias of the rest potential would cause the hyperpolarized end to electroporate earlier than the depolarized end. Quantitatively, the asymmetry in r and N is very small, and it is unlikely that this minor variation would be detectable experimentally. This offset disappears during the initial charging transient because the nearly step increase in N increases the electroporation current or pore current by four orders of magnitude that supports the rest potential. The electrical behavior of the cell is governed by rest potential and pore current, even in regions which are not electroporated. The intrinsic rest potential of the cell plays an important role for nano pore formation into the both layer of intraorganelle.

The electrostatic pressure, surface tension and rest potential have great influences on pore energy, pore density as well as pore radius. We have shown that free energy pore is gradually decrease with the increase of radius of the pore for hydrophilic pore but for hydrophobic pores the pore energy is expotentially increase with the increase of radius but independent of pressure. As per the polar location, the outer membrane pore density is non uniform but independent of pressure whreeas in innermembrane pore density is depends on pressure.The maximum pores are exposed at theta (θ) = 100° and value of pore density is direcly proportional with the electrostatic pressure of membrane. Analytically the pore density is linearly increased whereas pore radius is exponentially increase with the change of membrane pressure due to the different elestic property of the membrane. In this analytical and theoretical study we investigate that for large values of E_a, stress is always negative and the field may therefore reduce the membrane surface tension to zero, resulting in the total loss of cohesion of the phospholipid molecules and rupture the bi-layer membrane. This rearrangement may cause the formation of pore into the intraorganelle.

It also observed that the formation of pores in the membrane considers the energy balance in the membrane and reduction of energy due to the loss of the reshaped cut-out in the membrane surface. We also find that the nanopores are nonuniformly distributed appears on the both layer and the biggest nano pore is situated at theta (θ) = 90°. Outer membrane pore bigger than inner membrane in same surface whereas the maximum pore density is obtained at theta (θ) = 100° and it is uneffected by surface tension.It also revels that Although in polar position there is non effect on pore density but in numerical value the pore density is effected by surface tension.

The pore density is non uniformly distributed and maximum pore density is obtained at theta (θ) = 100° for both layer and value of pore density is inversely proportional with the rest potential. The intrinsic rest Potential (V_rest) of the cell will alter the pore density (N) and radius (r) profile by shifting it in the direction of Vrest. N and r at the poles would still be symmetric about the equator, but they are at that location would be equal to the rest potential. Quantitatively, the asymmetry in r and N is very small, and it is unlikely that this minor variation would be detectable experimentally. The electrical behavior of the cell is governed by rest potential and pore current, even in regions which are not electroporated. The intrinsic rest potential of the cell plays an important role for nano pore formation into the both layer of intraorganelle.

To summarize, the behavior of lipids and water within the bilayers differs, depending on whether a pore is induced by an electric field or by mechanical stress. In the presence of an electric field, water becomes highly oriented. Pores form with little change in surface area. It is observed that the surface tension and pressure developed in intra organelle pore current are non uniformly distributed over the both membrane of osteoblast cell in different magnitude and polar position and their profile is cosine in nature. We also explore the effect of pressure, surface tension and rest potential on pore energy, pore density and pore radius, which are the key component of intraorganelle nanoporation. All the results in our current research provides the new information regarding life cycle and viability of intra organelle nano pores of regid bone cell like osteoblast that enhanced the concept of drug delivery system in bone cell.