Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2013) Volume 2, Issue 2
The mispricing of the deep-in-the money and deep-out-the-money generated by the Black and Scholes model is now well documented in the literature. In this paper, we discuss different option valuation models on the basis of empirical tests carry out on the French option market. We examine methods that account for non-normal skewness and kurtosis, relax the martingale restriction, mix two log-normal distributions, and allows either for jump diffusion process or for stochastic volatility. We find that the use of a jump diffusion and stochastic volatility model performs as well as the inclusion of non normal skewness and kurtosis in terms of precision in the option valuation.
<Keywords: Implied Volatility, Stochastic Volatility Model, Jump Diffusion Model, Skewness, Kurtosis
The failure of the Black and Scholes [1] model to provide correct valuation is attributable to the parsimonious assumptions used to derive the model. One of the strong assumptions of the model is that security prices follow a constant variance diffusion process with logreturns normally distributed whereas the constant variance assumption has always been rejected by many studies.
The ARCH models literature set up by Engle [2] and Bollerslev [3] has been devoted to the volatile behavior of stock return variances. This empirical literature has proved the stochastic nature of stock return variances and their correlation with security price levels shoing that returns are both skewed and leptokurtic. The systematic deviations from the observed prices correspond to a “gap” in the option valuation as noticed Black (1975) when stating that “one possible explanation for this pattern is that we have left something out of the formula”.
As Rubinstein [4] notice, the Black and Scholes [1] model tends to systematically misprice in-the-money and out-the-money options. Different studies lead to different conclusions knowing whether this model underprices deep-out-of-the-money and overprices deep-inof- the-money options or the contrary. Nevertheless, Rubinstein [4] concluded that the bias direction can change across different periods. The biases are not in the same direction for all markets and they are not constant over time. Observed moneyness biases constitute evidences against the hypothesis that asset returns are homoskedastic and normally distributed; this gave an impulse to the development of option pricing models for alternative processes.
The Constant Elasticity of Variance option pricing model of Cox and Ross [5] relax the constant volatility hypothesis and enabled the instantaneous conditional volatility of asset returns to depend deterministically upon the level of asset price. The implied binomial tree models of Dupire (1994), Derman and Kani (1994), and Rubinstein (1994) can be considered as flexible generalizations of the CEV model while the stochastic volatility option pricing models of Scott [6], Wiggins [7], Johnson and Shanno (1987) use numerical methods as the Monte Carlo simulations to price options when the variance varies.
Hull and White [8] solve explicitly for the options price by using Taylor expansion. But to produce analytical results they imposed the correlation between increments to be null. They solve the case for non zero correlation through Monte Carlo simulations. Hull and White [9] derive a model in series expansion form allowing for instantaneous correlation between stochastic volatility and the stock price.
Stein and Stein [10] derive a closed-form solution when volatility is driven by an Ornstein-Uhlenbeck (AR1) process but with zero correlation between both increments. Heston [11] proposes a closedform solution, but with arbitrary correlation between volatility and spot returns.
Jarrow and Rudd [12] approximate the log-normal probability distribution by an arbitrary distribution in terms of a series expansion. The idea is to derive an option pricing model expressed as the sum of the [1] formula plus adjustment terms permitting to capture the impact on the option price of the third and fourth moments of the underlying security stochastic process. In the same manner, Corrado and Su [13] derive and test empirically a European option pricing model that extends the [1] model to take into account for non-normal skewness and kurtosis in the distribution of stock returns.
The skewness and kurtosis coefficients are estimated simultaneously along with the implied standard deviation. They find that the adjustments for skewness and kurtosis are effective in removing systematic strike price biases from Black-Scholes [1] model for S&P500.
The recognition that asset returns are leptokurtic, especially for short periods, incited [14] to look for option pricing through jumpdiffusion processes. Ball and Torous [15,16] propose a simplified version of the jump-diffusion model known as the as the Bernoulli Jump process. Later on, Maltz [17] fitted this model to market option price data in order to estimate the ex-ante probability distribution of exchange rates. Bates [18] fit a jump diffusion option pricing model to option data extracting implicit volatility, skewness and kurtosis.
Duan [19] develops a GARCH option pricing model capable of reflecting the changes in the conditional volatility using numerical simulation. Ritchken and Trevor [20] developed also an option pricing model using a lattice algorithm to price both American and European options under discrete time GARCH processes. We recall that [21] showed that the GARCH model can be written as an approximation to certain diffusion equations which has been postulated in the option pricing literature. Duan, Gautier and Simonato [22] propose a series approximation to value American options for GARCH processes with one lag in the variance dynamics. Heston and Nandi [23] develop a closed-form option valuation formula for an asset whose variance follows a NGARCH process.
In this paper, we adopt Whaley’s [24] simultaneous equations procedure to estimate the implied parameters serving for the calculation of the option prices. This paper is organized as follows. Section 2 presents the models that are implemented. Section 3 gives details about sampling methodology. Section 4 displays the empirical results. Section 5 assesses the statistical performance of the models. Section 6 summarizes and concludes.
We compare the out-of-sample performances of different option pricing models using the Black-Scholes [1] model as a benchmark.
Skewness and kurtosis adjusted model
The expansion methods are now largely used in quantitative finance. The idea is to start with an expansion formula for the risk neutral density considered as a general probability distribution. The first term of the expansion corresponds either to log-normal or normal distribution. The following terms can be therefore considered as successive corrections to the log-normal or normal approximations. The series is truncated at a finite order fixed empirically, which gives a parametric approximation of the risk neutral distribution. From this expression, we can derive an option pricing formula. The only drawback of this method is that when the infinite sum in the expansion represents a probability distribution, finite order approximations of it may become negative, leading to negative probabilities far enough in the tails, which generates severe mispricing for options that are far enough from the money.
We follow the approach of Corrado and Su [13] in the use of a semiparametric option pricing formula. They use the Gram-Charlier series expansion to model the distribution of stock log-prices. This method focuses on the skewness and kurtosis deviations from normality. Stuart and Ord (1987) discussed the distinction between Edgeworth expansion and Gram-Charlier expansion. To obtain an option pricing formula that correct the bias of the Black-Scholes [1] model, they add to this formula, adjustment terms accounting for non normal skewness and kurtosis. For a density function f(x), the Gram-Charlier series expansions are defined as:
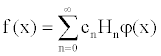
φ(x) is a normal density function and H(x) are Hermite polynomials derived from successively higher derivatives of φ(x) while the coefficient Cn are determined by moments of the distribution function F(x). The Gram-Charlier series, which are infinite series, are here truncated to eliminate terms after the fourth moment. This turns out to be a good proxy for option pricing due to the consideration of non-normal skewness and kurtosis. A truncated series that take into account skewness and kurtosis gives the following density function with centered mean and reduced variance for the following density:
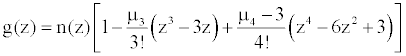
with
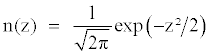
Under risk-neutral measure, one can apply the density function g(z) to derive a formula for a European call as being the present value of an expected payoff at expiration. This call price is derived from the following expression:
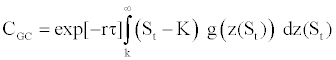
where
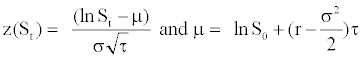
We obtain an option pricing call formula based on the Gram- Charlier series as being:
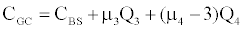
where
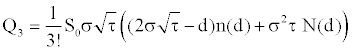
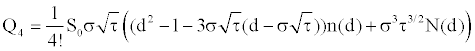
with
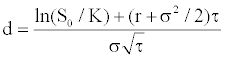
Implicit stock price adjusted model
The principle of the no-arbitrage approach is that the price of an option is obtained by taking the expectation of its discounting payoffs relative to a risk-neutral density. Arbitrage is not feasible in the condition that the risk-neutral density mean satisfy the martingale restriction. This restriction states that the price of the underlying asset implied by the option price must be the same that its observed market price, otherwise its should means the existence of arbitrage opportunities within a market with no frictions as shown by Harrisson and Kreps [25].
In the situation of frictions in the market, the option prices are determined by equilibrium and not by no-arbitrage reasoning, thus, the martingale restriction need not to be met. Among the frictions that can be encountered in the market, such as transaction costs or illiquidity, we can add information costs. The idea of estimating an implicit stock price is not recent. Manaster and Rendleman [26] is the first to invert [1] formula to estimate daily implied stock prices and daily implied volatility parameters. They concentrate their work around the idea of forecasting returns using the implied stock price.
They find that the implied stock price exceeds the observed price and affirmed that implied prices contain information regarding equilibrium stock prices that is not totally reflected in observed stock prices. One other reason to explain the difference between both stock prices was that transactions between both markets were not synchronous and thus, the difference represents more a recent rather than better information.
However, if they find that the second hypothesis explains a large part theses differences, “it is still possible that a significant fraction of implied prices represents more recent information than observed stock prices”. Later on, Longstaff [27] carries out a similar test on what he called “the martingale restriction”. He uses S&P100 index options data from 1988 to 1989, with American call options for which the American exercise effect should be alleviated. He focuses on a five minute window from 2:00 PM to 2:05 PM using index values during this window.
He find that the implied S&P100 index cost is superior to the actual index cost for 442 cases out of 444 daily estimates by an amount of 1.004. He explaines that since an option can be seen as a levered position in the underlying asset, which means that purchasing a stock through the option market costs more than on the spot market. We intuitively understand that accessing to a derivative market implies additive costs such as transaction or information costs.
Comparing the Black-Scholes [1] model with an equilibrium version of the model in which the martingale restriction is relaxed, he obtaines that, more than a half of the pricing errors occurring with the [1] model, is eliminated. We note that Patilea, Ravoteur and Renault (1995) propose an econometric approach based on the concept of implicit stock prices applied to the Hull and White [8] model and Renault [28] explains that introducing an implicit stock price may explain the skewness observed in the smile.
In this paper, we don’t test the martingale restriction following the very same methodology of Longstaff [27], we just want to check whether relaxing the martingale restriction, i.e, estimating an implicit stock price, will improve in our context the option pricing. We don’t limit ourselves to a small time period window since we don’t have enough observations per window.
Mixture of lognormal distributions
Melick and Thomas [29] estimate option pricing as a mixture of log-normal densities. They consider that the risk-neutral density can be adjusted correctly as a mixture of various log-normal densitites, representing different views of future reality. This method integers a number M of log-normal distributions but we limit our case to the simple case M=2. We suppose the risk-neutral density being equal to:
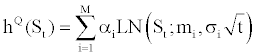
with
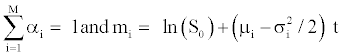
and LN(St;mQ,σ2t) is the log-normal density function under riskneutral measure. Within this configuration, the investors can imagine a situation for the future where, for instance, two configurations are expected, for which they affect two probabilities α1 and α2 and where the asset growth rate will be subject to two drift dynamics (μ1 and μ2) and two volatilities (σ1 and σ2). The call price of a mixture of log-normal densities can be written as:
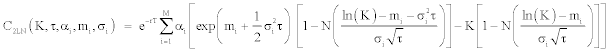
Under the risk-neutral probability, we impose the following constraint:
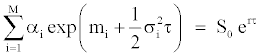
The advantage of the procedure is that the option prices are given as an average of the Black-Scholes [1] prices for different volatilities weighted by the respective weights of each distribution in the mixture. By construction, this mixture of log-normals has thin tails unless one allows high values of variance. As recall Campa, Chang and Reider [30], probability in the tails declines monotonically and always decays quickly enough for preventing unrealistic kurtosis. The only drawback of this procedure is that it is not supported by any theoretical economic background, which could lead to a lack of economic meaning.
Stochastic volatility model
Hull and White [9] consider the following stochastic processes for the returns and for the volatility through the risk-neutral data generating process given by:
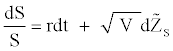
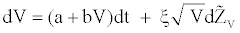
where a, b, and ξ are constant and 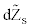 and
and 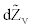 are Wiener processes under risk-neutral probability and r is the instantaneous interest rate supposed constant. V is the asset’s instantaneous variance rate. In order to ensure that the drift rate of V will not be negative, it is required that a≥0. From the dynamic of the variance, we can obtain a constant drift with b=0, a constant proportional drift with a=0 or a mean reverting process with a>0 and b=0 from which V will tend to revert to a longrun level –a/b with a mean reversion rate –b. The time required for the expected deviation to be halved, the half-life is given by –ln2/b.
are Wiener processes under risk-neutral probability and r is the instantaneous interest rate supposed constant. V is the asset’s instantaneous variance rate. In order to ensure that the drift rate of V will not be negative, it is required that a≥0. From the dynamic of the variance, we can obtain a constant drift with b=0, a constant proportional drift with a=0 or a mean reverting process with a>0 and b=0 from which V will tend to revert to a longrun level –a/b with a mean reversion rate –b. The time required for the expected deviation to be halved, the half-life is given by –ln2/b.
Hull and White [9] set up a power series expansion procedure based on the security price distribution conditional on the average value of the stochastic variance. This technique remains one of the most tractable one since if one compare it to the analytical approach proposed by Heston [11] based on Fourier inversion method. As in Corrado and Su [13], we set in the series expansion, the variance being equal to its long run reversion value since it is a credible hypothesis; however, running the model as it appears in the Hull and White [9] article is not more difficult, it simply requires an additional parameter to be estimated. Under this expansion, they showed how to correct the bias in the [1] model using a precise approximation from a second order Taylor series expansion:
Bias correction = 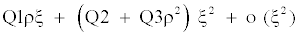
The terms of the series expansions are defined as:
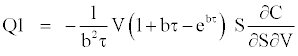
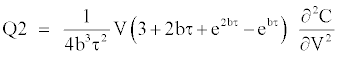
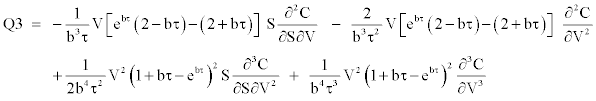
We obtain a stochastic-adjusted call price when adding the bias correction to the Black and Scholes [1] call price, which yields:
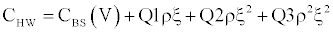
If we assume a constant process variance, i.e, ξ = 0, we collapse in the Black and Scholes [1] formula since the pricing bias is null.
Jump diffusion model
The research of a distribution that fit the best the behavior of stock returns still continue to be a dominant issue in finance. After the introduction of arithmetic and geometric Brownian motions, much attention was devoted to Poisson distributions as a valid specification of stock returns. In addition to empirical evidence, these models succeeded in capturing the “abnormal” components of the total change in stock price as recalled Ball and Torous [15], while the “normal” component, considered as marginal changes, is captured by a standard log-normal diffusion process.
We know that large values of returns occur too often to be consistent with normality and also, positive and negative returns of a given size are not equally likely. We observe kurtosis if jumps in either direction are equally likely and we observe in addition skewness, if jumps in one direction are larger or more frequent. Both skewness and kurtosis are captured by the Poisson distribution as noticed Jorion [31]. However, as recalled Renault [28], the expansion of these models are limited to the fact that there are few cases where closed-form solutions are given, specifically when there is a non zero probability of early exercise, or when the distribution of jumps is neither lognormal nor discrete. We follow Maltz [17] for pricing options with Jump Diffusion Model. In this section we assume that follows a log-normal jump diffusion, i.e., the addition of a geometric Brownian motion and a Poisson jump process. This price process under the risk-neutral probability can be shown to be:
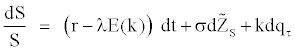
with qτ a Poisson counter with average rate of jump occurrence λ (prob(dq = 1) = λdt) and k the jump size. [15-17] suppose as a simplification that during the life of the option there will occur at most one jump of constant size. If no events occur in the option life, the associated probability is (1–λτ) and will be λτ if one event occurs during this time interval. When such event occurs, there is an instantaneous jump in the stock price. This simplified version is called by Ball and Torous [15,16] as the Bernoulli distribution version of the jump-diffusion model:
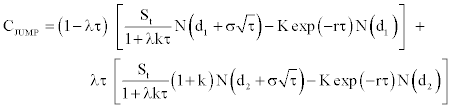
where:
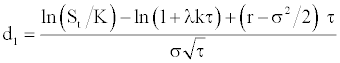
and:
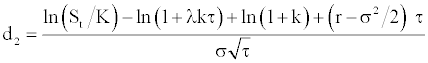
This formula corresponds to the Black and Scholes [1] call option value weighted by the probability of a jump and by the probability of no jump with the stock price divided by the expected value of a jump (1–λkτ).
The description of the data
Option prices are extracted from SBF-BOURSE DE PARIS. The data set contains the PXL option quotations, the strike prices, the maturity and the CAC 40 quotations during October 1998. We use intra-day observations for all quotations. The PXL options are European style options that are written on the CAC 40 Index. Our study is based on call options. Their maturity lasts 6 month. The interest rate is taken from DATASTREAM. We chose the PIBOR 6 months as the risk-free interest rate. For the dividend yield, we use ex-post dividend rate downloaded from DATASTREAM.
The sampling methodology
We have in total 1402 intra-daily observations that represent option premium and all the features linked to these options, such as, the strike price, the underlying index price, the maturity, the minimum number of purchasable options, the risk-free interest rate. The maturity chosen is March 1999 and the minimum number of purchasable options is 50. The PIBOR interest rate is a daily rate.
To each option quote, correspond two intra-minutes CAC 40 quotes, since the index is quoted every 30 seconds, which means that there is a quotation for the first 30 seconds of a minute and another quotation for the last 30 seconds. We retain only the quotation pertaining to the first 30 seconds of the minute as underlying quote. We delete each quotation resembling exactly to the following.
There are 600 out-of-the-money calls and 28 in-the-money calls, i.e. 628 calls. There are 554 out-of-the-money puts and 220 in-themoney puts, i.e. 774 puts. For our study, we consider the 600 out-ofthe- money calls and the 554 out-of-the-money puts due to the fact they are more traded; they represent 1154 observations. We transform the out-of-the-money puts into theoretical observed in-the-money calls. Using the Black and Scholes [1] formula as a function, we extract the volatility by equating the function with the corresponding premium. Using this extracted volatility and the other corresponding parameters of the out-of-the-money puts, we re-compute through the Black and Scholes [1] formula for a call, a theoretical price of a supposed in-themoney call.
We don’t display the results showing the out-of-sample performance of the Black and Scholes [1] model as a benchmark. We first estimate daily implied standard deviation (ISD) of call options written on the CAC 40 index from intra-day data sample. We calculate a prior-day ISD and we use it as an input to compute the current-day option price. Theoretical Black and Scholes [1] prices based on an outof- sample ISD are then compared to their corresponding observed prices. The next models follow the same procedure.
First estimation procedure
We compute the Skewness and Kurtosis-adjusted Black and Scholes [1] option price model. We estimate the ISD, the option implicit skewness SK and the option implicit kurtosis KU, through the Simultaneous Equations Procedure, which gives us implied values of our parameters by minimizing the following sum of squares:
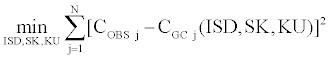
CGC(ISD,SK,KU) is the call price of the proposed model computed with the ISD parameter and which includes the implied third and four moments SK, KU. This call price is calculated for any option in a given current day’s sample.
Column 7 gives the details about the results obtained by the comparison between the skewness and kurtosis-adjusted [1] model and the corresponding observed prices in the market. The average deviation spread in is computed as follows:
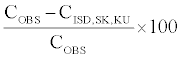
Table 1 gives the results obtained from the first estimation procedure.
| Trading date | Number of data | ISD (%) | Option Implied Skewness ISK | Option Implied Kurtosis IKU | Proportion of Theoretical Prices Different from the Observed Prices at ± 1 % | Average Spread between Observed and Theoretical Price (%) | Average Deviation of Theoretical Price from Observed Prices (FF) | Average Call Price (FF) |
| 02/10/98 | 153 | 49.416 | -1.083 | 3.151 | 0.810 | 28.702 | 20.378 | 419.250 |
| 05/10/98 | 69 | 47.436 | -1.062 | 2.831 | 0.696 | 1.909 | 17.839 | 528.873 |
| 06/10/98 | 53 | 45.694 | -1.025 | 2.815 | 0.698 | 2.564 | 16.868 | 506.300 |
| 07/10/98 | 49 | 45.580 | -1.195 | 3.712 | 0.673 | 19.961 | 20.444 | 406.673 |
| 08/10/98 | 56 | 46.754 | -1.027 | 2.821 | 0.804 | 31.224 | 19.376 | 441.110 |
| 09/10/98 | 41 | 48.173 | -1.447 | 4.203 | 0.659 | -7.466 | 19.913 | 338.436 |
| 12/10/98 | 68 | 43.203 | -1.196 | 2.883 | 0.985 | -3.986 | 23.798 | 500.436 |
| 13/10/98 | 55 | 42.325 | -1.253 | 2.894 | 0.400 | 1.082 | 18.696 | 626.313 |
| 14/10/98 | 86 | 42.859 | -1.366 | 3.789 | 0.651 | 0.435 | 12.718 | 345.208 |
| 15/10/98 | 59 | 40.170 | -1.195 | 2.907 | 0.864 | 11.065 | 16.228 | 378.210 |
| 16/10/98 | 60 | 39.765 | -1.371 | 2.903 | 0.700 | -5.325 | 14.172 | 385.422 |
| 19/10/98 | 32 | 39.941 | -1.366 | 2.852 | 0.719 | 3.327 | 9.551 | 395.641 |
| 20/10/98 | 88 | 39.165 | -1.289 | 2.916 | 0.580 | 7.274 | 11.190 | 526.652 |
| 21/10/98 | 57 | 40.007 | -1.299 | 2.885 | 0.667 | 6.378 | 11.160 | 564.885 |
| 22/10/98 | 47 | 39.291 | -1.330 | 2.893 | 0.532 | -1.952 | 10.054 | 566.498 |
| 23/10/98 | 31 | 40.482 | -1.269 | 2.827 | 0.903 | 24.462 | 15.179 | 391.574 |
| 26/10/98 | 25 | 38.303 | -1.148 | 2.817 | 0.760 | 11.033 | 18.150 | 341.497 |
| Average | 64.111 | 42.857 | -1.222 | 3.054 | 0.712 | 7.688 | 16.219 | 451.166 |
All the observed prices correspond to call options traded in October 1998 in the MONEP.
Table 1: Comparison of non normal skewness and kurtosis model prices and observed prices of PXL call options.
We notice that the average implied volatility is about 42.86% with a spike observed the second day reaching 49.41%. The average percentage obtained for the option implied skewness is -1.22. The average implied kurtosis is 3.05. We see in column six that in average, 71.2% of the theoretical prices are outside the ± 1% spread applied in the observed prices. Using the Black and Scholes [1] model, we obtain for the calls an average of 97.1%, which signifies a gain of about 26 %. The average deviation is around 16.22 FF (column 8) for an average call price of 451.16 FF (column 9). The average spread between the observed price and the corresponding theoretical price is about 7.68%, which indicates that the mispricing generally observed in the different models is significantly reduced with this model. Figure 1 shows the effects of allowing non-normal skewness and kurtosis in the theoretical ISD Black and Scholes [1] formula on October, 2nd 1998. We recall that positive moneyness signifies out-of-the-money options and negative moneyness implies in-the-money options. We see that this model reduces sharply the price deviation or bias effect observed in figure 1. This constitutes a clear improvement in terms of precision in the option valuation.
Second estimation procedure
We compute the implicit stock price in addition to the implied volatility from the Black and Scholes [1] model. We estimate the ISD, the option implied volatility and IS, the implicit underlying asset price, through the Simultaneous Equations Procedure, which gives us implied values of our parameters by minimizing the following sum of squares:
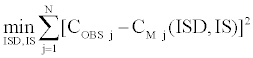
CM(ISD,IS) is the call price of the second model computed with the ISD parameter and IS, the implied stock price. This call price is calculated for any option in a given current day’s sample (Table 2).
| Trading date | Number of data | ISD (%) | Option Implied Stock Price IS | Proportion of Theoretical Prices Different from the Observed Prices at ± 1 % | Average Spread between Observed and Theoretical Price (%) | Average Deviation of Theoretical Price from Observed Prices (FF) | Average Call Price (FF) |
| 02/10/98 | 153 | 38.158 | 3036.741 | 1.000 | -60.031 | 76.532 | 419.250 |
| 05/10/98 | 69 | 37.506 | 3097.794 | 0.942 | -19.283 | 45.895 | 528.873 |
| 06/10/98 | 53 | 37.433 | 3150.394 | 0.830 | -16.927 | 50.194 | 506.300 |
| 07/10/98 | 49 | 34.885 | 3203.877 | 0.959 | -44.953 | 33.987 | 406.673 |
| 08/10/98 | 56 | 37.989 | 3045.192 | 1.000 | -68.087 | 79.396 | 441.110 |
| 09/10/98 | 41 | 30.986 | 3213.468 | 0.976 | -11.808 | 54.859 | 338.436 |
| 12/10/98 | 68 | 32.368 | 3316.699 | 1.000 | 14.847 | 72.750 | 500.436 |
| 13/10/98 | 55 | 33.166 | 3339.479 | 0.836 | -1.775 | 39.135 | 626.313 |
| 14/10/98 | 86 | 28.806 | 3422.876 | 0.919 | -8.973 | 32.703 | 345.208 |
| 15/10/98 | 59 | 30.550 | 3457.335 | 0.847 | -6.200 | 33.062 | 378.210 |
| 16/10/98 | 60 | 29.257 | 3496.891 | 0.900 | -2.293 | 24.723 | 385.422 |
| 19/10/98 | 32 | 29.516 | 3492.022 | 0.938 | -9.126 | 22.979 | 395.641 |
| 20/10/98 | 88 | 32.620 | 3477.614 | 0.898 | -3.893 | 32.953 | 526.652 |
| 21/10/98 | 57 | 32.520 | 3492.155 | 0.947 | -12.402 | 31.770 | 564.885 |
| 22/10/98 | 47 | 33.129 | 3503.112 | 0.915 | -8.276 | 36.129 | 566.498 |
| 23/10/98 | 31 | 28.902 | 3500.633 | 0.968 | -49.638 | 36.298 | 391.574 |
| 26/10/98 | 25 | 30.023 | 3529.909 | 0.960 | -6.669 | 29.141 | 341.497 |
| Average | 64.111 | 33.035 | 3339.776 | 0.931 | -18.558 | 43.089 | 451.166 |
All the observed prices correspond to call options traded in October 1998 in the MONEP.
Table 2: Comparison of implicit stock price model and observed values of PXL call options.
We notice that the average implied volatility is about 33.03% with a spike observed the second day reaching 38.16%. The average percentage obtained for the option implied stock price is 3339.77. We see in column five that in average, 93.1% of the theoretical prices are outside the ± 1% spread applied in the observed prices. Three of them are completely outside, which indicates a very slight improvement, but that is not significant relative to our benchmark, i.e., the Black and Scholes [1] model. The average deviation is around 43.09 FF in column 7 for a average call price of 451.16 FF. The average spread between the observed price and the corresponding theoretical price is about -18.56%, which indicates that the mispricing generally observed in the benchmark is reduced by two. Figure 2 shows the effects of estimating implicitly the stock price in the theoretical Black and Scholes [1] formula on October, 2nd 1998. We globally see that options around the money are generally all over-estimated. The estimation failed to provide an improvement in terms of price deviation. 16 out of 18 daily implicit stock prices are superior to the observed stock prices and the average difference between them is about 2.27% with a median value at 2.54% and about 2.50% when compared to the average of observed values in the day.
Third estimation procedure
In this procedure, we compute an option price as a mixture of two log-normal distributions. We estimate two implied volatilities and m1, m2, α1, α2 through the Simultaneous Equations Procedure, which gives us implied values of the parameters. The Simultaneous Equations Procedure minimizes the following sum of squares:
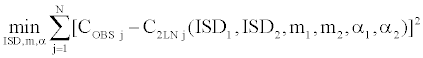
C2LN(ISD1, ISD2, m1, m2, α1, α2) is the call price of the proposed model computed for any option in a given current day’s sample (Table 3).
| Trading date | ISD1 (%) | ISD2 (%) | m1 | m2 | α1 | Proportion of Theoretical Prices Different from the Observed Prices at ± 1 % | Average Spread between Observed and Theoretical Price (%) | Average Deviation of Theoretical Price from Observed Prices (FF) |
| 02/10/98 | 36.503 | 39.046 | 8.047 | 8.042 | 0.848 | 1.000 | -60.557 | 76.632 |
| 05/10/98 | 46.494 | 10.486 | 7.841 | 8.236 | 0.685 | 0.986 | 5.865 | 39.746 |
| 06/10/98 | 26.979 | 41.575 | 8.211 | 7.854 | 0.404 | 1.000 | -18.158 | 41.204 |
| 07/10/98 | 19.579 | 68.446 | 8.187 | 7.595 | 0.606 | 0.918 | -18.724 | 27.639 |
| 08/10/98 | 34.642 | 33.996 | 8.070 | 8.013 | 0.834 | 1.000 | -66.727 | 79.382 |
| 09/10/98 | 41.005 | 11.800 | 7.889 | 8.250 | 0.725 | 0.976 | 10.982 | 40.351 |
| 12/10/98 | 30.449 | 32.399 | 8.079 | 8.024 | 0.827 | 0.971 | 15.293 | 75.205 |
| 13/10/98 | 23.065 | 45.590 | 8.196 | 7.776 | 0.685 | 0.945 | 3.711 | 33.933 |
| 14/10/98 | 31.404 | 43.655 | 8.113 | 8.045 | 0.862 | 0.930 | -8.326 | 31.660 |
| 15/10/98 | 26.341 | 45.359 | 8.157 | 7.968 | 0.837 | 0.864 | -6.018 | 32.795 |
| 16/10/98 | 17.729 | 55.596 | 8.257 | 7.736 | 0.652 | 0.817 | 5.180 | 15.740 |
| 19/10/98 | 44.034 | 18.006 | 7.947 | 8.260 | 0.441 | 0.875 | -4.066 | 14.355 |
| 20/10/98 | 45.498 | 16.593 | 7.898 | 8.271 | 0.442 | 0.955 | 7.003 | 30.265 |
| 21/10/98 | 51.874 | 16.550 | 7.890 | 8.269 | 0.419 | 0.526 | -1.264 | 15.680 |
| 22/10/98 | 45.592 | 17.366 | 7.916 | 8.275 | 0.424 | 0.872 | 4.011 | 22.267 |
| 23/10/98 | 47.876 | 19.694 | 7.909 | 8.266 | 0.390 | 1.000 | -26.642 | 42.918 |
| 26/10/98 | 19.857 | 17.260 | 7.950 | 8.286 | 0.411 | 0.960 | 11.267 | 23.085 |
| Average | 50.495 | 15.995 | 7.961 | 8.256 | 0.425 | 0.917 | -8.657 | 37.815 |
All the observed prices correspond to call options traded in October 1998 in the MONEP.
Table 3: Comparison of mixture of lognormal distribution model and observed values of PXL call options.
We notice that the average implied volatility is about 50.50% for ISD1 and three times less for ISD2 with 16%. We see in column seven that in average, 91.7% of the theoretical prices are outside the ±1% spread applied to the observed prices. Four of them are completely outside, which indicates a slight improvement, but that is not significant relative to our benchmark.
The average deviation is around 37.81 FF in column 9 for an average call price of 451.16 FF. The average spread between the observed prices and the corresponding theoretical prices is about -8.66%, this is an improvement in pricing compared to the benchmark (Figure 3) shows the effects of considering a mixture of two log-normal distributions on October, 2nd 1998.
This form of estimation failed to provide an improvement in terms of price deviation and we observe that the prices generated by this mixture are globally the same than those generated by the implicit stock price model.
Fourth estimation procedure
We estimate implicitly the parameters of the Hull and White [9] model. We estimate the correlation parameter ρ, the volatility of volatility parameter ξ and the coefficient of mean reversion b and the ISD through the Simultaneous Equations Procedure, which gives us implied values of our parameters by minimizing the following sum of squares:
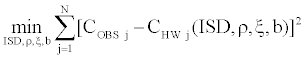
CHW(ρ, ξ, b) is the call price of the Hull and White [9] model. This call price is calculated for any option in a given current day’s sample (Table 4).
| Trading date | Number of Data | ISD (%) | Implied Volatility of Volaility | Implied Correlation | Half-Life Of Volatility (Days) | Proportion of Theoretical Prices Different from the Observed Prices at ± 1 % | Average Spread between Observed and Theoretical Price (%) | Average Deviation of Theoretical Price from Observed Prices (FF) |
| 02/10/98 | 153 | 44.397 | 2.655 | -0.560 | 21.357 | 0.974 | 35.785 | 30.525 |
| 05/10/98 | 69 | 43.575 | 2.101 | -0.696 | 21.229 | 0.913 | 16.722 | 25.472 |
| 06/10/98 | 53 | 41.858 | 2.994 | -0.520 | 21.443 | 0.943 | 13.139 | 19.630 |
| 07/10/98 | 49 | 41.391 | 2.241 | -0.624 | 21.253 | 0.898 | 33.809 | 21.958 |
| 08/10/98 | 56 | 42.251 | 3.156 | -0.478 | 21.456 | 1.000 | 52.034 | 28.610 |
| 09/10/98 | 41 | 41.497 | 1.856 | -0.717 | 21.165 | 1.000 | 0.751 | 20.252 |
| 12/10/98 | 68 | 40.347 | 2.531 | -0.629 | 21.333 | 0.897 | 3.734 | 25.566 |
| 13/10/98 | 55 | 40.843 | 3.549 | -0.460 | 21.563 | 0.818 | 5.202 | 22.714 |
| 14/10/98 | 86 | 37.122 | 4.496 | -0.421 | 21.795 | 0.860 | 6.620 | 15.132 |
| 15/10/98 | 59 | 35.363 | 2.082 | -0.715 | 21.224 | 0.966 | 44.622 | 25.641 |
| 16/10/98 | 60 | 35.043 | 1.699 | -0.655 | 21.127 | 0.983 | 0.208 | 21.515 |
| 19/10/98 | 32 | 36.232 | 2.337 | -0.652 | 21.278 | 0.938 | 10.951 | 23.923 |
| 20/10/98 | 88 | 35.031 | 2.936 | -0.526 | 21.415 | 0.932 | 12.970 | 22.693 |
| 21/10/98 | 57 | 36.609 | 2.577 | -0.516 | 21.316 | 0.947 | 12.752 | 27.162 |
| 22/10/98 | 47 | 35.676 | 3.063 | -0.495 | 21.437 | 0.872 | 2.533 | 18.458 |
| 23/10/98 | 31 | 37.675 | 2.873 | -0.512 | 21.392 | 0.968 | 34.398 | 26.174 |
| 26/10/98 | 25 | 34.912 | 3.101 | -0.486 | 21.445 | 0.920 | 17.998 | 20.984 |
| Average | 64.111 | 39.038 | 1.858 | -0.606 | 21.157 | 0.931 | 17.896 | 23.318 |
All the observed prices correspond to call options traded in October 1998 in the MONEP
Table 4: Comparison of implicit Hull and White (1988) model and observed values of PXL call options.
The average percentage obtained for the implied correlation parameter is –0.60. We see in column five that in average, 93.1% of the theoretical prices are outside the ± 1% spread applied to the observed prices. Two of them are completely outside, which indicates a very slight improvement, but that is not significant relative to our benchmark. The average deviation is around 23.32 FF in column 9 for a average call price of 451.16 FF. The average spread between the observed price and the corresponding theoretical price is about 17.89%, which shows that the mispricing generally observed in the benchmark is reduced two times. (Figure 4) shows the effects of estimating option prices with a stochastic volatility model on October, 2nd 1998.
The Hull and White [9] model provides significant improvements in terms of price deviations for far from the money call options.
Fifth estimation procedure
We estimate implicitly the parameters of the jump diffusion model. We estimate the jump occurrence parameter λ, the jump size parameter k and the implied volatility through the Simultaneous Equations Procedure, which gives us implied values of three parameters by minimizing the following sum of squares:
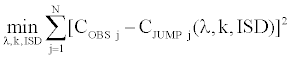
CJUMP(λ, k, ISD) is the call price given by the jump diffusion model. This call price is calculated for any option in a given current day’s sample (Table 5).
| Trading date | Number of data | ISD | Option Implied Jump Occurrence | Option Implied Jump Size | Proportion of Theoretical Prices Different from the Observed Prices at ± 1 % | Average Spread between Observed and Theoretical Price (%) | Average Deviation of Theoretical Price from Observed Prices (FF) | Average Call Price (FF) |
| 02/10/98 | 153 | 0.273 | 0.377 | -0.537 | 0.778 | 4.490 | 17.148 | 419.250 |
| 05/10/98 | 69 | 0.279 | 0.421 | -0.537 | 0.768 | -13.107 | 16.414 | 528.873 |
| 06/10/98 | 53 | 0.269 | 0.387 | -0.544 | 0.642 | -6.343 | 14.829 | 506.300 |
| 07/10/98 | 49 | 0.272 | 0.359 | -0.542 | 0.857 | -17.044 | 16.482 | 406.673 |
| 08/10/98 | 56 | 0.259 | 0.389 | -0.509 | 0.875 | 6.844 | 17.806 | 441.110 |
| 09/10/98 | 41 | 0.265 | 0.397 | -0.538 | 0.805 | -9.838 | 15.616 | 338.436 |
| 12/10/98 | 68 | 0.237 | 0.517 | -0.473 | 0.926 | -6.087 | 19.867 | 500.436 |
| 13/10/98 | 55 | 0.254 | 0.382 | -0.498 | 0.582 | -3.704 | 17.429 | 626.313 |
| 14/10/98 | 86 | 0.254 | 0.341 | -0.510 | 0.709 | -5.438 | 10.354 | 345.208 |
| 15/10/98 | 59 | 0.233 | 0.421 | -0.471 | 0.763 | -12.297 | 11.351 | 378.210 |
| 16/10/98 | 60 | 0.225 | 0.415 | -0.467 | 0.767 | -3.076 | 10.705 | 385.422 |
| 19/10/98 | 32 | 0.227 | 0.397 | -0.463 | 0.563 | -1.906 | 7.855 | 395.641 |
| 20/10/98 | 88 | 0.211 | 0.477 | -0.440 | 0.693 | -1.053 | 19.192 | 526.652 |
| 21/10/98 | 57 | 0.237 | 0.335 | -0.492 | 0.596 | -1.349 | 17.138 | 564.885 |
| 22/10/98 | 47 | 0.254 | 0.270 | -0.536 | 0.574 | -5.698 | 15.451 | 566.498 |
| 23/10/98 | 31 | 0.249 | 0.268 | -0.533 | 0.871 | -5.348 | 14.571 | 391.574 |
| 26/10/98 | 25 | 0.214 | 0.516 | -0.427 | 0.920 | -6.417 | 15.680 | 341.497 |
| Average | 64.111 | 0.239 | 0.297 | -0.529 | 0.746 | -5.139 | 15.170 | 451.166 |
All the observed prices correspond to call options traded in October 1998 in the MONEP.
Table 5: Comparison of jump diffusion model prices and observed prices of PXL call options.
We notice that the average implied volatility is about 24 %. The average percentage obtained for the implied average rate of jump occurrence is 0.297 and the implied average jump size is about –0.53. About 74.62% of the theoretical prices are lying outside the ±1% spread applied to the observed prices. No one is totally outside, showing that the improvements that brings this jump diffusion model.
The total gain relative to the benchmark is about 23 %. The average deviation is around 15.17 FF for an average call price of 451.16 FF. The average spread between the observed prices and the corresponding theoretical prices is about –5.14 %, which indicates a considerable decrease in the mispricing. Figure 2 shows the effects of allowing one jump of constant size in the theoretical [1] framework on October, 2nd 1998 (Figure 5).
The reduction in the price deviation is clear comparing to the benchmark and is very comparable to model 2 and model 5.
We want to evaluate the statistical significance of the improvement in terms of performance from out-of-sample adjustments brought by each model and for that, we use the following Z-statistic that represents the difference between the two proportions, P1 and P2 Hoel (1984):
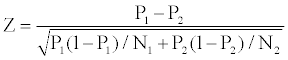
P1 and P2 are sample proportions, while N1 and N2 are corresponding sample sizes.
We obtain after computation:
For the first model: Z=18.218 - P1=0.971 and P2=0.712; N1=N2= 1154
For the second and fourth model: Z=4.470 - P1=0.971 and P2=0.93; N1=N2=1154
For the third model: Z=5.680 - P1=0.971 and P2=0.917; N1=N2=1154
For the fifth model: Z=16.383 - P1=0.971 and P2=0.746; N1=N2=1154
The Z-statistics of 4.470, 5.680 and 18.218 are statistically significant at more than 99.99% confident level, which corresponds to a fractile of 2.32.
We want to go further into the analysis of the out-of-sample performance of our various models. We denote C, the observed price of the option and C , the theoretical price of the same option. We use the Mean of Absolute forecast Error (MAE) and the Mean Absolute Percentage forecast Error (MAPE) (Lauterbach and Schultz (1990)). For n being the number of options, the value of the MAE is equal to the mean of the difference in absolute value between the observed prices and the theoretical prices:
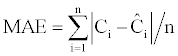
For each option the valuation error percentage is given by:
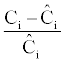
The MAPE value is:
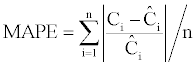
The value of MAE and MAPE are actually complementary because if the first one gives a classical estimation of the difference, the second one gives the difference relative to the theoretical price. Tables 6 and 7 give the results obtained using the PE, MAE and MAPE measures (Table 6).
| Models | MAE | MAPE | PE |
| Benchmark | 38.827 | 0.209 | 1.206 |
| I - Series expansions | 11.248 | 0.413 | -1.668 |
| II - Martingale restriction | 40.760 | 0.171 | -1.312 |
| III - Mixture of log-normals | 36.818 | 0.146 | 0.030 |
| IV - Stochastic volatility | 18.589 | 0.628 | 10.497 |
| V - Jump diffusion | 10.007 | 0.0632 | -0.899 |
The pricing errors are computed as the difference between the observed call price and the theoretical price.
Table 6: Comparison between alternative models.
| Models | MAE | MAPE | PE | |||
| ITM | OTM | ITM | OTM | ITM | OTM | |
| Benchmark | 41.673 | 36.271 | 0.061 | 0.342 | 42.806 | -36.349 |
| I - Series expansions | 9.785 | 12.563 | 0.014 | 0.772 | -0.514 | -4.783 |
| II – Martingale restriction | 60.235 | 23.262 | 0.0869 | 0.247 | 28.734 | -12.489 |
| III – Mixture of log-normals | 55.285 | 20.225 | 0.074 | 0.211 | 20.146 | -1.045 |
| IV – Stochastic volatility | 22.418 | 15.149 | 0.03 | 1.166 | 21.717 | 0.336 |
| V - Jump diffusion | 12.24 | 8 | 0.0165 | 0.105 | -0.907 | -4.389 |
Table 7: Comparison between alternative models for ITM and OTM call options.
The jump diffusion model holds the best MAPE and MAE and the second best pricing errors while the stochastic volatility model has surprinsingly the worst MAPE and pricing errors. (Table 7) presents the forecast errors distinguishing in-the-money options and out-themoney options.
We observe that the series in expansion model produces the best forecasts concerning ITM options for PE, MAE and MAPE measures. However, the best MAE and MAPE measures concerning OTM options, are obtained by the jump diffusion model, which has also the second best pricing error measure. The martingale restriction model has the worst performance among the five other models. The two models (1 and 5) that overestimate the ITM options have the best PE; the only model (4) that underestimates the OTM options has also the best PE. We globally note that the stochastic volatility model and the series in expansions model suffer form severe mispricing of OTM options.
In this paper, we carry out empirical tests of different models likely to correct the pricing bias that occurred in the classical Black and Scholes [1] framework and we also test the statistical performance of the given models. We observed that the Black and Scholes [1] model undervalues out-the-money calls and overvalues in-the-money calls. The jump diffusion model performs better than the other four models and overall has the best results concerning the out-the-money call options while the series in expansion model holds the best forecasts concerning the in-the-money call options. The stochastic volatility model arrives in third position with no outstanding performances. As for the mixing two log-normal distibutions and the implicit stock price model, they didn’t offer the expected precision. In further research, we will extend this work to propose an option valuation model that incorporates both transaction costs and information costs in order to correct the bias due to the frictions in the market.