Journal of Medical Diagnostic Methods
Open Access
ISSN: 2168-9784
ISSN: 2168-9784
Research Article - (2016) Volume 5, Issue 1
Objective: The aim of this study was to optimize the performance of an Adaptive Neuro-Fuzzy Inference System (ANFIS) in terms of its connection weights which is usually computed based on trial and error when used to diagnose Typhoid fever patients.
Methods: This research proposed the use of Genetic Algorithm (GA) technique to automatically evolve optimum connection weights needed to efficiently train a built ANFIS model used for Typhoid fever diagnosis. The GA module computes the best set of connection weights, stores them, and later supplies them to the corresponding hidden layer nodes for training the ANFIS. The medical record of 104 Typhoid fever patients aged 15 to 75 were used to evaluate the performance of the multi-technique decision support system. 70% of the dataset was used training data, 15% was used for validation while the remaining 15% was used to observe the performance of the proposed system.
Results: From the evaluation results, the proposed Genetic Adaptive Neuro Fuzzy Inference System (GANFIS) achieved an average diagnosis accuracy of 92.7% compared to 85.4% recorded by the ANFIS method. It was equally observed that the diagnosis time was much lower for the proposed method when compared to that of ANFIS.
Conclusion: Therefore, the proposed system (GANFIS) has the capability to attenuate the key problems associated with Neuro-Fuzzy Based diagnostic methods if fully embraced and as well it could be adopted to solve challenging problems in several other domains.
Keywords: Decision support system; Fuzzy logic; Neural network; Genetic algorithm; Typhoid fever; Diagnosis
The administration of efficient healthcare services has been a major challenge in developing countries due to inadequate healthcare delivery personnel and the inappropriate diagnostic techniques often adopted. In most parts of the tropics, the diagnosis of TF is based on smear microscopy and Widal test, while in rare cases it includes bacterial culture [1]. However, in rural settings of Africa, clinical diagnosis (based on symptoms) remains the only option for TF diagnosis and this makes accurate diagnosis unlikely. Research has equally reported poor diagnosis as a major hindrance to efficient management of TF in developing countries. Several factors including lack of good water supply, high prevalence of asymptomatic infections in rural communities, improper waste management system, insufficient access to trained healthcare providers, inadequate healthcare facilities, and widespread practice of self-treatment for clinical suspected TF, contributes to poor diagnosis of TF in the tropics [1,2]. Acute TF may be severe depending on the clinical setting and the quality of available medical care, up to 10% of typhoid patients may develop serious complications [3]. Accurate and timely diagnosis often aids the administration of therapy which at the long run improves patients’ health status [4].
Quite a number of methods have been proposed for the Diagnosis of TF [5-9]. Among these methods, Neuro-Fuzzy based approach seems promising because of its high level of diagnosis accuracy. In short, the problem with neural networks (NN) is that a number of parameter such as optimal number of hidden nodes, selection of the relevant input variables and selection of optimal set connection weights has to be set before training can begin [10]. However, there are no clear rules on how to set these parameters. Yet these parameters determine the success of the training of the neural network [11]. Despite the promising results Quite a number of methods have been proposed for the Diagnosis of TF [5-9]. Among these methods, Neuro-Fuzzy based approach seems promising because of its high level of diagnosis accuracy. In short, the problem with neural networks (NN) is that a number of parameter such as optimal number of hidden nodes, selection of the relevant input variables and selection of optimal set connection weights has to be set before training can begin [10]. However, there are no clear rules on how to set these parameters. Yet these parameters determine the success of the training of the neural network [11]. Despite the promising results
This research proposes an enhanced diagnostic decision support system which adopts genetic algorithm technique to optimize the performance of a neuro-fuzzy diagnostic method. The proposed system consists of a Fuzzy logic (FL) component which uses Mamdani inference technique, and takes as input the key attributes of TF diagnosis, the NN component was designed to compute the membership function parameters needed by the FL module for prediction, while the Genetic Algorithm component was designed to automatically generate a set of optimal connection weights needed to efficient train the NN. The proposed system is built with the aim of providing a decision support platform with the capability to aid medical practitioners in administering efficient diagnosis outcome for TF patients. The remaining part of this paper is structured as follows: Section 2 presents review of related work; Section 3 presents the architecture of the proposed system, method and materials adopted by the research; Section 4 presents experiment and results; Section 5 presents the evaluation results of the proposed system; while Section 6 presents the conclusion of the research.
Soft computing
The understanding, processing or solving of complex problems require intelligent systems that combine knowledge, techniques and methodologies from various sources [12]. Therefore, intelligent systems should aggregate human knowledge in a specific domain, adapt and learn the best way possible in environments that are constantly changing. For this reasons, it is of great advantage to use several computational techniques instead of just one, which is the essence of our geneticneuro- fuzzy technique: genetic algorithm which generate optimal set of solutions from a given population, neural networks that recognize patterns and are able to adapt to changes and the fuzzy inference system that incorporates human knowledge for making decisions. Typically a fuzzy system incorporates a rule base, membership functions and an inference procedure and has been recording success in systems that handles ambiguous elements [13,14].
Fuzzy logic
Fuzzy Logic (FL) is a form of many-valued logic which deals with reasoning that is approximate rather than fixed and exact. Compared to traditional binary sets (where variables may take on true or false values), fuzzy logic variables may have a truth value that ranges in degree between 0 and 1 [15]. Due to the flexibility of FL concept, Fuzzy Logic Systems (FLSs) have attracted growing interest in modern information technology, production technique, decision making, pattern recognition, data mining, and medical diagnosis among others [16-19]. FL has found a variety of applications in industrial process control and securities trading [20-23]. It has equally been employed in the modeling of medical diagnosis systems [24-27]. Figure 1 presents the architecture of a typical FLS.
A typical FLS is strongly based on the concepts of fuzzy sets, linguistic variables and approximate reasoning. The fuzzifier transforms crisp inputs into fuzzy values while the Fuzzy Rule Base makes up the Knowledge Base which stores relevant data and knowledge of human experts in a specific domain; the Decision-making unit combines all the fired rules for a given case and makes inference; while the defuzzifier converts fuzzy results into a crisp value for easy analysis and interpretations.
Generally, when a problem has dynamic behavior and involves several variables, FL technique can be applied to solve such problem [28]. However, a major problem of the FLSs is the determination of its fuzzy sets and fuzzy rules which require deep knowledge of human experts in a particular domain [5]. The Membership Functions (MFs) of FLSs are arbitrarily chosen, therefore fixed in nature. Generally, the shape of the MFs depends on certain parameters that can be adjusted. Rather than choosing the MF parameters arbitrarily, the neural network learning and tuning techniques provides a method for the FLS to learn information about a given dataset in order to automatically compute its MF parameters.
Neural networks
Neural Networks (NNs) are a family of statistical learning algorithms inspired by biological neural networks (the central nervous systems of animals, in particular the brain) and are used to estimate or approximate functions that can depend on a large number of inputs. They are equally seen as large number of highly inter-connected processing elements (nodes) that demonstrate the ability to learn and generalize from training patterns or data. Research has proved NN as an excellent tool for developing systems that can perform the same type of information processing tasks that our brain performs [29,30]. NN was traditionally referred to as a network or circuit of biological neurons [31]. Figure 2 shows the model of a perceptron (A single layer NN).
The perceptron is a single layer NN whose weights and biases could be trained to produce a correct target vector when presented with the corresponding input vector. The training technique used is called the Perceptron Learning Rule. A Perceptron is especially suited for simple problems in pattern classification. The inputs received by a single processing element (depicted in Figure 2) can be represented as an input vector Xi = (X1, X2), where Xi is the signal from ith input. A weight is associated with each connected pair of neurons. Hence, weights connected to the jth neuron can be represented as a weight vector of the form Wj = (W1j, W2j), where Wij represents the weight associated to the connection between the processing elements Xi and Xj respectively. Y which is the output represents the activation function (f) of the weighted sum of all incoming signals.
A combination of NN and FL techniques provides a solution that is capable of integrating the strength of both and eliminating their weaknesses [32]. Therefore, this hybrid technique provide a method that allows the NN model to learn the required information from a given dataset and compute the MF parameters that best drives the associated FIS [33]. Neuro-Fuzzy systems still suffer a major setback in terms of optimal connection weights for the NN model. However, optimization technique such as Genetic Algorithm could be employed to solve this problem.
Genetic algorithm
The Genetic Algorithm (GA) is a method for solving both constrained and unconstrained optimization problems that is based on the principle of natural selection, a process that drives biological evolution. GA employs a search technique based on the concept of evolution [34], and in particular with the concept of the survival of the fittest [35]. The technique is conceptually based on evolution mechanism which works on population of solutions in contrast to other search techniques that work on a single solution [36]. The workability of GA is based on Darwinian’s theory of survival of the fittest. GA usually contains a chromosome, a gene, a set of population, fitness function, breeding, mutation and selection. GA technique begins with a set of solutions represented by chromosomes, called population. Solutions from one population are taken and used to form a new population, which is motivated by the possibility that the new population will be better than the old one. Further, solutions are selected according to their fitness score to form new solution known as offspring. The above procedure is repeated until certain conditions are satisfied [37]. Its basic implementation involves the following processes: Initial population generation; Fitness evaluation; and the Application of genetic operations of Selection, Crossover, and Mutation and it usually provide acceptable solution within a reasonable time frame when solving optimization problems [38,39]. In summary, GA has the capability of evolving the best set of connection weights for optimal training of NN. Therefore, there is need to apply GA technique in order to automatically generate a set of connection weight that would be used to the NN module.
Proposed system’s architecture
Figure 3 present the overall architecture of the proposed Multi technique driven decision support system. It consists of a Knowledge Base (KB), Genetic-Neuro-Fuzzy Inference Engine (GNFIE), Decision Support Engine (DSE) and a User Interface which serves as a medium for entering diagnosis variables and displaying diagnosis results. The details of the components of Figure 3 are presented in subsequent subsections.
The attributes considered for the diagnosis of TF after consultations with medical experts and standard literature in the field of tropical medicine is presented in Table 1.
| S/N | Category | TF diagnosis attributes | Code |
|---|---|---|---|
| 1 | Elevated Liver Function Test | Q1 | |
| 2 | Patient Laboratory Investigation (PLI) | Blood Test | Q2 |
| 3 | Stool Test | Q3 | |
| 4 | Urine Test | Q4 | |
| 5 | Fever | Q5 | |
| 6 | Headache | Q6 | |
| 7 | Abdominal Pain | Q7 | |
| 8 | Patient Medical History (PMH) | Stomach Pain | Q8 |
| 9 | Myalgia | Q9 | |
| 10 | Lassitude | Q10 | |
| 11 | Loss of Appetite | Q11 | |
| 12 | Vomiting | Q12 | |
| 13 | Patient Physical Examination(PPE) | Body Temperature | Q13 |
| 14 | Pulse Rate | Q14 |
Table 1: Categories of typhoid fever diagnosis attribute.
Fuzzy logic component
The FL component of Figure 3 is made up of a fuzzifier, fuzzy inference engine, and a defuzzifier. The fuzzifier converts crisp input values to their corresponding fuzzy values. Assuming v is a fuzzy set of diagnosis variables in V (Universe of Discourse) and xi represents an element in v, then v is:
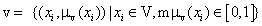 (1)
(1)
where vμ ( xi) is the Membership Function (MF) of ( xi) in v and it represents the degree of contribution of ( xi) towards the diagnosis outcome of TF. The fuzzy set employed by this research to describe the attributes of TF diagnosis consist of; very mild, mild, moderate, severe, and very severe. Each diagnosis attribute in Table 1 is represented by a linguistic term that belongs to the defined fuzzy set, while each linguistic term has its associated numeric value. For example, the linguistic term of the ith diagnosis variable is defined by equation (2) as follows:
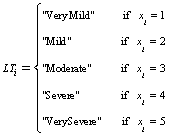 (2)
(2)
where LTi represents the linguistic term for the ith diagnosis variable, i = 1, 2, 3,…,14; and xi (Qi) denotes the value of the ith diagnosis variable. Figure 4 shows the MF graph of input variables which represents the degree of contribution for each input variable towards the diagnosis outcome.
The knowledge of medical experts employed in the diagnosis of TF is represented in the Rule Base using “If Then” construct. The number of rules (NR) in each category of diagnosis attribute was computed using equation (3)
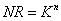 (3)
(3)
where K is the number of linguistic variables considered in the fuzzy set, and n is the number of variables in each category of diagnosis attribute. The rule base therefore contains rules that assume the following format:
IF FEV is Mild AND HDA is Very Mild AND…. THEN TF is Mild.
where FEV and HDA are the input variables and “TF is Mild” is the output of the diagnosis. Both the inputs and output have their associated linguistic term drawn from the given fuzzy set above. Detail description of the Fuzzy Inference System operation is presented in ref. [4].
Neural network component
The NN component of Figure 3 is made up of attributes of patient medical history, patient physical examination, and patient laboratory investigation. This component learns certain information from the above modeled FIS in order to automatically generate the required MF. The resulting output at each stage of the NN model is given by equations 4 and 5. The values of TF diagnosis variables (Q1-Q14) are supplied to the network via the input layer and the outcome of each category of diagnosis variables is determined at the hidden layer of the network as shown in equation (4).
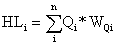 (4)
(4)
HLi is the Hidden Layer diagnosis result for the ith category (node), n is the number of variables in HLi and Qi is the ith diagnosis variable with corresponding weight WQi .
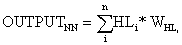 (5)
(5)
The result of the NN output is computed by equation (5), where WHLi is the connection weight of HLi result. Note that the neurons in each layer are connected to the ones in the succeeding layer by a link known as connection weight which is generated by the GA module in order to produce the desired outcome.
Genetic algorithm component
The Genetic Algorithm (GA) component of Figure 3 evolves the optimal connection weights for the NN component by providing the best set of parameters for training the NN. The GA implementation procedure adopted by this research work involves four basic steps (Initial population generation, Selection, Crossover, and Mutation) [40,41]. GA is classed into two based on the level at which learning is modeled. A first possibility is a model of population learning where rules specifying some actions are set up. A number of variations have been developed to improve performance of GAs on problems with a high degree of fitness epistasis. In this possibility, learning is modeled before exploiting the beneficial phenotypic interactions of the genes and as such, they are aligned with the building block hypothesis in adaptively reducing disruptive recombination. Hence, fitness of a rule is determined by members of the population executing their specified action, and thus observing a feedback generated from the environment. The other possibility is modeling individual learning by means of genetic operators like crossover, mutation or intermediate and discrete recombination. Basically this is a classifier designed to solve problems in real-value domain by adjusting control parameters of the search that is, self-adaptation. In this study, the former GA method was adopted in order to obtain the optimal sets of NN weights required for training the NN model within the shortest time.
The procedure for the adopted GA technique is described as follows: from the NN in Figure 5, suppose p is the number of input nodes, q, the numbers of nodes in the hidden layers, and r, the nodes at the output layer, then the link (connection weight) between the ith node of the input layer and the jth node of the hidden layer is Wij. The set of connection weights from the input layer to the hidden layer is therefore {W11, W12, . . . , Wnq} while the set of weights between the hidden layer nodes and the output layer nodes is {W11, W21, . . . , Wqr}. Since the NN structure in Figure 5 has one output node, then r = 1 and the set of weights becomes {W11, W21, W31, . . ., Wq1}. A gene was represented by the connection weight Wij. The total number of connection weights is equivalent to the total number of genes while the chromosome which is an embodiment of genes is encoded as a string of genes as follows:
Chromosome = {gene1, gene2, gene3, . . ., genen} (6)
Equation (6) also corresponds to the set of connection weights which is show in equation (7)
Connection Weights = {W11, W12, W13, …, Wnq, W11, W21, W31,…, Wqr} (7)
N = (p*q) + (q*r) (8)
where N represents the total number of nodes in the NN. This research adopted a hybrid encoding scheme (Binary and Real Value encoding) for the encoding of genes (connection weights) and the Cost function respectively [42]. The Binary encoding technique is explained as follows: Given a set of genes, such that each gene is encoded with a five binary bits. For example if a gene has a value of 4, then the binary encoded equivalent is 00111. Meanwhile, the first bit of the encoded string denotes the sign bit which could be 0 (Negative) or 1 (Positive). In this research work, -10 and +10 (01010 and 11010) forms the lower and upper bounds of the set from which all genes (connection weights) were drawn. The following Binary encoded genes denote inputs to the NN.
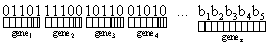
where z denotes the total number of genes employed in the NN. For instance, gene1 denote the connection weight of the first diagnosis variable (Q1), gene2 denote the connection weight of the second diagnosis variable (Q2) and so on. The Real value encoding converts binary encoded genes to their real value equivalent as follows: Given that
genei = {b1, b2, b3, . . . , bM} (9)
such that b1 is the sign bit and M is the length of genei, the function that computes the sign bit of the ith gene is:
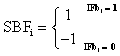 (10)
(10)
where SBFi denotes the Sign Bit Function for the ith gene. Finally, the Real value encoding of the ith gene is computed by equation (11).
 (11)
(11)
Where, RVEi represents the Real Value Encoding for the ith gene in the chromosome.
The NN model in Figure 5 has fourteen input nodes which denote the input diagnosis variables, three hidden layer nodes which represent the intermediate diagnosis results and one output layer node which represent the overall diagnosis result. In summary, there are a total of seventeen connection links each with its weight (gene). Figure 6 is an equivalent of Figure 5 but this time around with a set of connection weights ready for training.
The initial population of chromosomes which was generated randomly and encoded in a fixed order from left to right, top to bottom and placed in list as shown by equation (12).
Chromosomes = {0.4 0.9 -0.4 0.2 0.5 0.6 0.1 -0.5 0.3 0.1 -0.1 0.8 0.7 0.6 0.4 0.2 0.3} (12)
In this research work a population of size P was set to 2N (where N is the total number of nodes in the NN). The suitability of each individual to the environment is tested by subjecting them to the fitness function (Fi) which is given by equations (13) and (14):
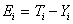 (13)
(13)
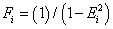 (14)
(14)
where Ei is the ith error term (low error means high fitness), Ti is the ith desired output, Yi is the ith actual output and Fi is the fitness value of the ith chromosome. Reproduction is achieved by a selection operation and in this process, structures with higher fitness values are duplicated while those with low fitness values are ignored. The fitness proportionate selection technique was adopted in this research work for selecting optimal individuals for the next generation of combination. A description of the evaluation procedure is given as follows:
The fitness function is first evaluated for each individual, providing fitness values which are then normalized. The normalized fitness value for each individual in the population is computed by equation (15).
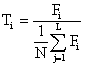 (15)
(15)
where j = 1, 2, 3 . . . L and Fi denote the probability of the ith chromosome to be selected for crossover and mutation. Hence, the population is sorted in descending order of fitness values while the accumulated normalized fitness (ΣLFi) values are computed. Finally, a random number R between 0 and 1 is chosen while the first individual with LF2 ≥ R is selected. This process is repeated until a complete set of optimal connection weights is achieved.
Genetic adaptive neuro fuzzy inference system (GANFIS)
The multi technique based diagnostic system (GANFIS) provides the ANFIS subsystem with the best set of connection weight. The ANFIS is made up of six layers of neurons in which the first, second, and fifth layers consists of adaptive nodes, while the third and fourth layers consists of fixed nodes. The layers are:
Layer 1: This layer consists of active nodes which denote inputs to the system. These inputs are numeric values which represents diagnosis variables drown from the following categories; PLI, PMH, and PPE. The output of this layer is the linguistic labels corresponding to each input value.
Layer 2: This layer is made up of adaptive nodes and the nodes receive as input the output of the preceding layer and produce their corresponding membership grade as shown in equation (16).
 (16)
(16)
There are various types of MFs, this research work adopted the triangular MF due to its ease of use and its formula is presented in equation (17).
 (16)
(16)
where a and b are the attributes of the triangular MF that bounds its shape such that b ≤ x ≤ a.
Layer 3: The nodes in this layer are fixed in nature and they are all labeled M indicating that they simply act as multipliers. The nodes in this layer compute the firing strengths of their associated rules. This layer’s output is represented by equation (18).
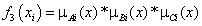 (18)
(18)
Layer 4: This layer is made up of fixed nodes labeled N and they normalize the firing strength of each rule. For example, the normalized firing strength of Rule 1 is shown in equation (19).
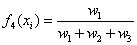 (19)
(19)
while the normalized firing strength of the kth Rule is given by equation (20).
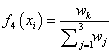 (20)
(20)
Layer 5: This layer is made up of adaptive nodes and the output of each node is the product of the normalized firing strength of a rule and its corresponding output value. This is shown in equation (21).
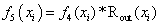 (21)
(21)
Layer 6: This layer consists of a single fixed node labeled Y which represents the final output. It is computed by summing all the incoming signals as shown in equation (22).
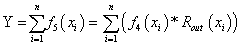 (22)
(22)
The final output of GANFIS is in crisp form and its represents the diagnosis result of a given patient. This crisp output is classified as Very Mild or Mild or Moderate or Severe or Very Severe, depending on its value by using equation (23).
 (23)
(23)
The medical records of 104 TF patients aged 15 to 75 were collected from the Federal medical center, Owo, Nigeria. This acquired data was analyzed and preprocessed to the required format. Matrix Laboratory (MATLAB) Version 8.0.0783 (R2012b) was used to implement the proposed system. Microsoft Access 2010 Version served as the Database for patient medical records while Microsoft Excel 2010 Version was used to preprocess the require dataset into a format that could be exported to MATLAB workspace. The signs, symptoms, and laboratory investigation for TF patients were rated as Very Mild (1), Mild (2), Moderate (3), Severe (4), and Very Severe (5). Table 2 shows the weight assigned to the diagnosis variables of patients after an extensive interaction with a medical doctor in the field of tropical medicine. The dataset was partitioned into three parts, the first (70%) was used for training the network, the second (15%) was used to validate the trained network, while the remaining part (15%) was used to test the performance of the proposed system.
| PatientID | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | Q9 | Q10 | Q11 | Q12 | Q13 | Q14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FMCO-001 | 3 | 3 | 1 | 1 | 5 | 4 | 4 | 3 | 5 | 3 | 4 | 3 | 4 | 2 |
| FMCO-002 | 4 | 4 | 3 | 1 | 4 | 3 | 2 | 3 | 4 | 3 | 1 | 3 | 3 | 3 |
| FMCO-003 | 4 | 2 | 4 | 3 | 2 | 1 | 5 | 4 | 3 | 4 | 3 | 4 | 5 | 1 |
| FMCO-004 | 1 | 3 | 2 | 2 | 3 | 2 | 2 | 4 | 5 | 3 | 4 | 3 | 3 | 4 |
| FMCO-005 | 5 | 2 | 2 | 4 | 3 | 4 | 3 | 2 | 2 | 2 | 3 | 3 | 3 | 2 |
| FMCO-006 | 3 | 1 | 1 | 2 | 4 | 2 | 1 | 3 | 3 | 3 | 3 | 5 | 4 | 4 |
| FMCO-007 | 2 | 3 | 4 | 3 | 3 | 5 | 4 | 2 | 2 | 1 | 1 | 2 | 4 | 5 |
| FMCO-008 | 2 | 2 | 4 | 2 | 5 | 3 | 3 | 2 | 4 | 3 | 4 | 3 | 4 | 3 |
| FMCO-009 | 2 | 3 | 2 | 2 | 5 | 4 | 2 | 2 | 3 | 3 | 3 | 1 | 2 | 1 |
| FMCO-010 | 1 | 2 | 3 | 1 | 3 | 2 | 4 | 3 | 1 | 1 | 2 | 4 | 1 | 1 |
| FMCO-011 | 3 | 3 | 1 | 1 | 4 | 3 | 2 | 2 | 3 | 2 | 5 | 1 | 5 | 2 |
| FMCO-012 | 4 | 2 | 2 | 1 | 4 | 2 | 2 | 3 | 1 | 1 | 3 | 2 | 1 | 2 |
| FMCO-013 | 3 | 3 | 2 | 1 | 3 | 4 | 1 | 3 | 1 | 2 | 3 | 2 | 3 | 1 |
| FMCO-014 | 1 | 1 | 2 | 2 | 3 | 3 | 2 | 1 | 4 | 2 | 3 | 2 | 5 | 5 |
| FMCO-015 | 1 | 1 | 2 | 4 | 3 | 2 | 1 | 2 | 1 | 1 | 1 | 2 | 2 | 4 |
| FMCO-016 | 2 | 2 | 1 | 2 | 3 | 1 | 5 | 3 | 3 | 4 | 2 | 2 | 1 | 1 |
| FMCO-017 | 3 | 3 | 3 | 5 | 3 | 3 | 4 | 2 | 3 | 1 | 4 | 5 | 3 | 3 |
| FMCO-018 | 3 | 2 | 1 | 2 | 1 | 2 | 2 | 3 | 1 | 1 | 2 | 1 | 1 | 3 |
| FMCO-019 | 1 | 2 | 4 | 1 | 2 | 4 | 3 | 3 | 2 | 4 | 3 | 3 | 4 | 1 |
| FMCO-020 | 3 | 4 | 4 | 2 | 4 | 5 | 5 | 4 | 4 | 3 | 2 | 5 | 4 | 3 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| FMCO-101 | 2 | 1 | 1 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
| FMCO-102 | 2 | 2 | 2 | 1 | 2 | 1 | 1 | 5 | 1 | 1 | 2 | 1 | 2 | 3 |
| FMCO-103 | 1 | 1 | 3 | 4 | 5 | 4 | 1 | 4 | 3 | 2 | 1 | 1 | 2 | 2 |
| FMCO-104 | 2 | 1 | 2 | 2 | 3 | 1 | 2 | 2 | 2 | 1 | 1 | 5 | 4 | 2 |
Table 2: Intensity of TF diagnosis variables.
Figure 7 shows the Genetic Algorithm module built to automatically compute the connection weights of the Neural Network component of the proposed system. This module computes the best set of weights needed by the hidden layers of the NN for training. It stores the weights and supplies the corresponding nodes with their respective weights for training. The graph in Figure 8 shows the Initial Fitness values for each individual in the first iteration (potential NN connection weight) with a Best fitness value of 0.00180071 and a Mean of 0.064424.
The graph in Figure 9 presents the Best, Worst, and Mean Scores of individual generations of the GA. In this figure, the 100th generation happens to be the worst while the 4th and 5th generations appears to be the Best and most probably contains the optimum connection weights for the NN training. Figure 10 represents a graph of the fitness level of each individual in the best generation, that is the 4th and 5th generations in Figure 10. From the information in Figure 10, it is evident that 12th individual has the highest score and there for represents the best individual of the generation followed by the 11th individual. The value of the best individual then represents the connection weight of the first node in of the NN and the same process is repeated until the all weights for the NN nodes are generated.
Performance evaluation often shows how valid a given system is in providing efficient solution. In an attempt to validate the efficiency of the proposed system, a comparative analysis of the diagnosis results of TF patients obtained from the conventional approach and that of the proposed system (GANFIS) was carried out in the first phase of the evaluation process as follows. Table 3 contains the diagnosis outcome of eight randomly selected patients using the conventional approach and the proposed method. Suppose P = {P1, P2, P3, P4, P5, P6, P7, P8} and S = {S1, S2, S3, S4, S5, S6, S7, S8} are sets of diagnosis results obtained from the conventional system and the proposed system respectively, then the empirical analysis of both set of results is presented in Table 3.
| Patient ID | FMCO-01 | FMCO-02 | FMCO-03 | FMCO-04 | FMCO-05 | FMCO-06 | FMCO-07 | FMCO-08 |
|---|---|---|---|---|---|---|---|---|
| DRCA | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
| DRPS | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
| ei | | P1-S1 | | | P2-S2 | | | P3-S3 | | | P4-S4 | | | P5-S5 | | | P6-S6 | | | P7-S7 | | | P8-S8 | |
| (1-ei) | [1-(P1-S1)] | [1-(P2-S2)] | [1-(P3-S3)] | [1-(P4-S4)] | [1-(P5-S5)] | [1-(P6-S6)] | [1-(P7-S7)] | [1-(P8-S8)] |
Table 3: Analysis of diagnosis results obtained from the conventional and the proposed systems.
Given that P = {P1, P2, P3, P4, P5, P6, P7, P8} = {0.56, 0.47, 0.61, 0.51, 0.49, 0.717, 0.670, 0.730} and S = {S1, S2, S3, S4, S5, S6, S7, S8} = {0.545, 0.45, 0.558, 0.484, 0.481, 0.683, 0.503, 0.451}, the replica of Table 3 with the required values is presented in Table 4.
| Patient ID | FMCO-01 | FMCO-02 | FMCO-03 | FMCO-04 | FMCO-05 | FMCO-06 | FMCO-07 | FMCO-08 |
|---|---|---|---|---|---|---|---|---|
| DRCA | 0.560 | 0.470 | 0.610 | 0.510 | 0.492 | 0.717 | 0.670 | 0.730 |
| DRPS | 0.545 | 0.450 | 0.580 | 0.484 | 0.481 | 0.683 | 0.503 | 0.451 |
| ei | 0.015 | 0.020 | 0.030 | 0.026 | 0.011 | 0.034 | 0.167 | 0.279 |
| ( 1-ei) | 0.985 | 0.980 | 0.97 | 0.974 | 0.989 | 0.966 | 0.833 | 0.721 |
Table 4: Analysis of diagnosis results obtained from the conventional and the proposed methods.
The mean accuracy of the proposed system and its efficiency are computed as shown in equations (24) and (25) respectively.
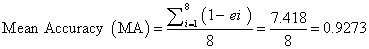 (24)
(24)
 (25)
(25)
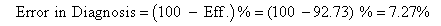 (26)
(26)
Therefore, from the outcome of the preceding statistical computations, it was deduced that the efficiency of proposed system in providing accurate diagnosis is 92.73%. Also, the time it takes the GA module to generate the optimal NN weights was significantly reduced compared to its manual equivalent.
In the second phase of the evaluation exercise, a comparative analysis of the proposed method (GANFIS) and that of an Adaptive Neuro-Fuzzy Inference System (ANFIS) was also carried out in terms diagnosis accuracy of TF. The eight randomly selected records were used to predict the diagnosis accuracy of the patients with respect to TF with GANFIS and ANFIS techniques. The errors in diagnosis for both techniques were computed by subtracting the diagnoses results of each method from that of the conventional method and then taking the absolute value. Finally, the diagnosis accuracy of each method (GANFIS and ANFIS) for the 8 randomly selected patients was determined using equation 27 and the results are presented in Figure 10.
Diagnosis accuracy = (1-ei) *100 (27)
where ei represents the error in diagnosis.
It can be seen from Figure 11 that out of a total of eight patients, our proposed method outperformed the ANFIS technique in terms of diagnosis accuracy for seven of the patients (Pat1, Pat2, Pat4, Pat5, Pat6, Pat7, and Pat8) except for the third patient (Pat3). The proposed technique (GANFIS) had an overall average diagnosis accuracy of 92.7% as against that of the ANFIS method which was 85.4% and this seem promising and could help increase the survivors of TF in the tropics and other parts of the world.
Also, it terms of diagnosis time, it could be seen from Figure 12 that the proposed system (GANFIS) has lower diagnosis time for all the patients compared to that of the conventional ANFIS which equally suggest that our proposed system would be more efficient.
A Multi-technic decision support system powered by genetic algorithm, neural network, and fuzzy logic concepts for the diagnosis of typhoid fever has been investigated in this study. An improved genetic algorithm concept was used to automatically supply the optimal set of weights needed to effectively train the neural network module. Usually, the membership function parameters of FIS are manually set thereby making it difficult for the FIS to provide accurate diagnosis results when confronted with new cases. To address this problem, the trained, validated, and tested neural network module was configured to automate the provision of membership function parameters for the fuzzy inference system, that is, building some form of learning and tuning capability into the fuzzy inference system. With this development, the fuzzy inference system was able to provide timely and reliable diagnosis outcome for new cases. The outcome of the evaluation process conducted in this research shows that the proposed system (GANFIS) had 7.27% with respect to the conventional diagnosis approach and it attained a diagnosis accuracy of 92.7% as compared to 85.4% of the ANFIS method. Also, in terms of time taken to diagnose a patient, the proposed system also performed better than the conventional ANFIS. Therefore, the proposed technique (GANFIS) has the capability to alleviate the key problems associated with Neuro-Fuzzy Based diagnostic methods if fully embraced and as well it could be adopted to solve challenging problems in several other domains.
We appreciate Dr. Oluwasanmi Olajide Samuel of the Federal Medical Center, Owo, Ondo State, Nigeria for providing us with the dataset and as well for his input to the research. Also, we thank the management of the Department of Computer Science, Federal University of Technology, Akure, Ondo State, Nigeria for their cooperation during this research project. Lastly, special thanks to the Chinese Academy of Sciences and the Institute of Biomedical and Health Engineering, Shenzhen Institutes of Advanced Technology, China for the opportunity to embark on this research project.