Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
+44-77-2385-9429
ISSN: 2168-9792
+44-77-2385-9429
Research Article - (2016) Volume 5, Issue 4
Axial flow compressors have a limited operation range due to the difficulty of controlling the secondary flows. Therefore, a new design of vortex generators is considered in the current investigation to control the secondary flow losses and consequently enhance the compressor’s performance. Different sets of curved side vortex generators with varying configurations are studied to find their effect on the secondary flow losses. Numerical simulations of a three-dimensional compressible turbulent flow have been performed to explore the effect of vortex generators on the reduction of secondary flow losses. Based on the simulation results, the pressure, velocity, and streamline contours are presented to track the development of secondary flows in the compressor cascade. Thus, the total pressure loss and static pressure rise coefficients, blade deflection angles, and diffusion factors are estimated. Results indicate that vortex generators have a significant impact on secondary flow losses such as reducing the corner vortices, and improving the location of separation lines which are moving toward the trailing edge. At the cascade design point, it is found that vortex generators have a significant effect on the reduction of normalized total pressure loss which is evaluated to be up to 20.7%. Using vortex generators do not lead to a significant change in flow deflection and accordingly the off-design conditions will still be far from reached.
<Keywords: Secondary flows; Axial compressors; Vortex generators; Turbulence
The importance of axial compressors due to its relevance to gas turbine applications has motivated many re-searchers toward enhancing its overall performance. Controlling the secondary flow phenomena associated with the flow in compressor cascades will significantly improve the aerodynamic performance of compressors. This is because secondary flows are extracting energy from the fluid and increasing the flow instability. Endwall boundary layer separation, horseshoe vortex, corner vortex, tip vortex, endwall crossflow, and passage vortex are secondary flow components in the cascade. Many researchers investigated the impact of three-dimensional blades and endwall boundary layer separation as well as flow separation in corners of blade passages on the development of secondary flows [1-5]. To control the secondary flows, both passive and active methods have been applied to reduce or overcome the effects of secondary flows in axial compressors. It was found that the passive control methods remain the preferable techniques because of their simplicity and cost effectiveness [6,7]. Numerous types of passive flow control devices were investigated such as slotted blading in linear cascades [8], vane and plow vortex generators placed on several positions [9], counter rotating and co-rotating rectangular, triangular, and parabolic vane type vortex generators [10-12], cavity as a control of shock wave interactions with the turbulent boundary layer [13], low profile vortex generators to reduce the boundary layer thickness [14], and doublet vortex generators [15]. An excellent comprehensive review of boundary-layer flow-separation control by a passive method and their applications had been compiled Lin JC [16,17].
There are numerous other reported studies on the control of separation in turbulent boundary layers using low profile vortex generators. In such devices, the mechanism of flow control is to energize the low momentum layers near a solid surface without adding extra energy through the momentum transfer from the outer (freestream) flow to the near wall region. Yet, this leads to an overwhelmed stronger adverse pressure gradient and hence avoids or delay the flow separation. In case of turbulent flow over a flat plate, experimental results indicated that the vane and wheeler type of vortex generators can efficiently reduce the flow separation. Using the vortex generator height (h/δ) of 0.1 to 0.4 was efficient with much reduce in the drag effect [18]. It was reported that flow control by means of vane-type vortex generator arrays is robust with respect to changes in the pressure gradient and changes of the separation point [19]. In addition, the van type with height (h/δ) of 0.8 attained the largest pressure recovery [20]. McCormick [21] experimentally compared between two passive methods for controlling shock induced separation on a turbulent flat plate boundary layer. A doublet wedge type vortex generator with h/δ=0.36 was used versus passive cavity (porous wall with a shallow Cavity underneath). He reported that the low-profile vortex generators were found to be significantly suppressing the shock induced separation and improve the boundary layer characteristics downstream the shock whereas the mass-averaged total pressure loss increased. In case of turbulent flow over backward facing ramp [22], wheeler doublet and wishbone type vortex generators were used to control flow separation. They concluded that both wheeler doublet and wishbone type achieved the best effect in separation control when their heights (h/δ) varied in the range of 0.1 to 0.2.
A theoretical investigation was conducted of three-dimensional turbulent flow provoked in a boundary layer by an array of low-profile vortex generators on the surface [23]. Triangular type vortex generators, with various span wise spacing were considered. He concluded several suggestions for vortex generator designs such spanwise packing, enlarged vortex generator length, and suitably of non-smooth spanwise profile. Recently, experimental and numerical studies of the effect of two vortex generator types with different configurations on the performance of the compressor cascade were conducted by Hergt [24]. They reported that at the cascade design point, the total pressure losses were reduced by about 9% with the vortex generator. Moreover, vortex genera-tors have a significant effect on the cascade deflection and a remarkable enhancement of the cascade stall range. However, the static pressure rise due to inserting a vortex generator was nearly unaffected.
To conclude, many types of low profile vortex generator devices were widely investigated for different applications. However, application on compressor cascade is still limited, and the optimal design and position of vortex generators to control the development of secondary flows are not fully established yet. Therefore, the objective of the present research is to investigate the influence of vortex generators on the development of secondary flows and flow separation zones of compressor cascade. Therefore, different sets of vortex generators with varying configurations are numerically studied. Based on the numerical results, pressure, velocity, and streamline contours are presented in order to track the development of the secondary flow losses. Furthermore, the total pressure loss coefficient, static pressure rises, blade deflection angles, and diffusion factors are estimated and discussed.
Compressor cascade
In the present work, a linear high speed compressor cascade that was reported by the research group of Hergt et al. [24] is used. Their compressor cascade was designed by “MTU Aero Engines”. The design parameters and the operating conditions of the cascade are summarized in Table 1. In addition, the inlet and staggered angles of the compressor cascade are shown in Figure 1.
| Mach number at inlet | M1 = 0.66 |
| Inlet flow angle | β1=132° |
| Turning angle | Δβ = 38° |
| Stagger Angle | βst =105.2° |
| Blade chord | c = 40 mm |
| Blade span | L = 40 mm |
| Pitch to chord ratio | s/c = 0.55 |
| End-wall boundary layer thickness at inlet | δ = 4 mm |
| Maximum blade thickness | t = 2.6 mm |
| Relative maximum camber | n/c = 0.446 |
Table 1: Compressor cascade design parameters and operating conditions.
Computational domain and boundary conditions
The computational domain used in the present work is depicted in Figure 2. The non-slip boundary condition is applied at the walls representing the top boundary, the bottom boundary (Endwall), and the blade surfaces demonstrating the suction and pressure sides including the leading and trailing edges. Periodic boundary conditions are applied on the domain sides. The pressure outlet boundary condition is defined at the outlet plane. The fully developed flow is adopted at the inlet with an average Mach number of 0.66 and inlet angle (β1) of 132°. Turbulence intensity is set to be 1% at the inlet and 3% at the exit. The blade is tested under the design operating conditions.
Numerical solution
To investigate the effect of inserting vortex generators with varying dimensions on secondary flow losses, the Reynolds-average Navier–Stokes with fully coupled turbulence model equations are numerically solved using the commercial flow solver Fluent-14. The three dimensional multiblock grid is constructed using a structured mesh of H-O-H topology. Five different numbers of grids are selected in order to investigate the effect of grid size on the computed results. Figures 3a and 3b present the effect of grid size on the mass flow averaged integrated velocity, and the velocity contours at (exit plane). Based on these figures, it is found that there is no grid dependency after 0.8 million cells. Therefore, the present simulation is performed using 1.2 million cells to get free grid independent results and to reduce the computational time and with minimum y+<1 near the walls, which is considered to capture and resolve the boundary layer at the blade surfaces and enwalls.
Computational investigations for curved side vortex generators (CSVGs) with and without a rounded nose are performed to find their effects on the development of secondary flows. The dimensions of studied sets of vortex generators named A, B, C, D, E, and F are summarized in Table 2. All tested CSVGs are shown in Figure 4, h/δ is varied from 0.1 to 0.5 for each set which is defined as low profile vortex generators as reported by [16].
| e/h | w/h | h/δ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 3 | 4 | 5 | 6 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 | |
| Set A | X | X | - | - | - | X | X | X | X | X | X | X |
| Set B | X | - | X | - | - | X | X | X | X | X | X | X |
| Set C | X | - | - | X | - | X | X | X | X | X | X | X |
| Set D | X | - | - | - | X | X | X | X | X | X | X | X |
| Set E | e/h | w/h | h/δ | |||||||||
| 4 | 5 | 6 | 8 | 6 | 0.4 | |||||||
| X | X | X | X | X | X | |||||||
| Set F | e/h | w/h | h/δ | r/δ | ||||||||
| 5 | 6 | 0.4 | 0.25 | 0.5 | 0.8 | 1 | ||||||
| X | X | X | X | X | X | X | ||||||
Table 2: Different parameters values for CSVG used in sets A, B, C, D, E and F.
This section is classified into six subsections. The first subsection demonstrates the validation of computational results by comparing with the available experimental data and numerical results. The second one depicts the influence of vortex generators on the development of secondary flows. The third subsection describes the influence of vortex generators on the total pressure loss coefficient. The influence of vortex generators on cascade deflection is shown in the fourth subsection. The fifth subsection illustrates the influence of vortex generators on the static pressure rise coefficient. In the last subsection, the influence of vortex generators on the diffusion factor is presented.
Validation
The numerical results are validated, first, by comparing between the isentropic Mach, Mis, distribution at mid span calculated from the numerical and the experimental results of Hergt et al. [24] as shown in Figure 5. Comparisons indicate that a good agreement exists between the present simulation and the experimental results where the maximum deviation is found to be less than 3.4%.
Second, the total pressure loss distribution is compared with the results obtained by Hergt [24] at the same plane (exit plane) as shown in Figure 6. Based on comparison, a reasonable agreement is observed where the maximum deviation is less than 4% except near the endwall. It reaches about +9%. Hergt et al. [24] reported that the predicted total pressure loss near the endwall is undepreciated the measured value, consequently the difference between the present results and measured by Hergt [24] is expected to be much less than 9%. Thereby the numerical method can predict the time-averaged blade loading with adequate engineering accuracy as appropriate boundary conditions are applied.
Figure 6: Mass flow averaged total pressure loss distribution of Hergt's simulation and the present simulation at a plane located at 40 % of chord behind the trailing edge.
Influence of vortex generators on the development of secondary flows
Streamline patterns are used to display the separation lines and the translations that occur to their positions on the suction surface for the different sets of vortex generators. Figures 7-9 illustrate the streamline contours on the suction side for different configurations of vortex generators of A, C, D, E, and F. Figure 7 shows the streamline contours for the reference case and set A where h/δ varies between 0.1 and 0.5 in step of 0.1. Based on Figure 7, comparisons between the reference set and other sets indicate that at h/δ=0.1, streamlines show how separation lines move at the suction surface. The cross flow from the endwall moves toward the leading edge where a new separation line and the formation of a separation bubble are observed. This occurs in the position between the cross flow and the corner separation while it moves slightly downstream. Increasing h/δ to 0.2 indicates that streamlines move to the corner separation downstream, and endwall cross flows are still developed and formed towards the leading edge. Furthermore, for h/δ=0.3, streamlines show a movement of the corner separation towards the trailing edge and a separation line is noticed near the corner separation region. Thus, causing the endwall cross flow to be deflected in the downstream direction. At h/ δ=0.4, streamlines show a noticeable displacement of the corner separation downstream, and so leading the endwall cross flow is to be translated in the downstream direction as well. In addition, the growth of previous formed separation lines occurs. Finally, at h/ δ=0.5, streamlines show regression of the corner separation towards the trailing edge, and at the same time the endwall cross flow deflects in the downstream direction, as well as the separation line near the corner region disappears. The changes in streamlines for set B is like that cause by A, so it is not reported.
Figure 8 shows the streamline contours for the reference case and set C where h/δ varies between 0.1 and 0.5 in interval of 0.1. Comparisons between the reference set and other sets indicate that at h/δ=0.1, streamlines show a translation of corner separation in the downstream direction towards the trailing edge. As the endwall cross flow propagates towards the leading edge, a separation bubble is noted between the endwall cross flow and the corner separation. However, at h/δ=0.2, no significant changes in streak lines are noted. At h/δ=0.3, streak lines also show a translation of the corner separation towards the trialing edge, and a formation of a separation line between the endwall cross flow and the corner separation. At h/δ=0.4, streak lines show a significant movement of the corner separation downstream towards the trailing edge, and the endwall cross flow is deflected in a downstream direction. However, the separation line formed in the previous case disappears. Finally, at h/δ=0.5, streak lines show that the corner separation is at 0.85 of chord (downstream) which is significantly translated, and the endwall cross flow is deflected in the downstream direction as well.
Figure 9 shows the streamline contours for the reference case and set D where h/δ varies between 0.1 and 0.5 in intervals of 0.1. Comparisons between the reference set and other sets indicate that at h/δ=0.1, the cross flow is slightly reduced meanwhile it propagates in the span direction, while separation lines do not display significant changes. Though, at h/δ=0.2, no significant changes in streak lines are noted. At h/δ=0.3, streamlines show a translation of the corner separation towards the trialing edge, a formation of laminar separation line between the endwall cross flows, a corner separation, and a turbulent reattachment line. At h/δ=0.4, streak lines are significantly moved from the corner separation region towards the trailing edge, and the endwall cross flow is deflected in the downstream direction. However, the separation line formed in the previous case disappeared. Finally, at h/δ=0.5, streak lines show that the corner separation is at 0.85 of chord (downstream) which is significantly translated, and the endwall cross flow is also deflected in the downstream direction.
To conclude, for all those sets, the pressure side effects the development of the passage vortex and its propagation which in turn affects the flow structure on the blade suction side. As a result of inserting the vortex generators, the passage vortex is lifted from the endwall and swept downstream which travels the separation line on the blade suction surface towards the trailing edge of sets A, C, and D. Increasing h/δ results in the downstream movement of this separation line as noted in the previous figures. For set E, increasing e/h leads to the increase of the downstream movement of the separation line on the blade suction surface. A similar trend is observed by increasing r/δ as set F.
Influence of vortex generators on total pressure loss coefficient
Total pressure loss coefficient (TPLC) is usually used as an indicator for losses that take place in a cascade. Reducing pressure losses tends to increase the cascade efficiency and consequently enhances the compressor performance. TPLC (ζ*) refers to local mass averaged total pressure loss coefficient (TPLC) and it can be defined as the following:
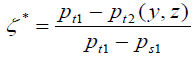 (1)
(1)
where: Pt1 is the total pressure at the inlet, and Pt2 (y,z) is the total pressure at the exit plane while, Ps1 is the static pressure at the inlet. TPLC is estimated as a function of (y, z) based on the calculated values at a plane downstream of the trailing edge at the distance of 0.45 of the chord (C). This plane is defined as the exit plane where variables computed at this plane take the index 2.
Total pressure loss coefficient contours: TPLC contours for set A, B, C, and D shows gradual change in the TPLC by increasing the dimensions of the VG. The reported results are from set D where the changes are very noticeable. Figure 10 shows the total pressure loss contours for set D. For set D, the total pressure loss contours are depicted for different values of h/δ varied from 0.1 to 0.5 in intervals of 0.1 along with the contours for the reference case. As reported earlier, the reference case is related to the flow in the compressor cascade without the vortex generator. Comparisons between the TPLC for reference case and those for different values of h/δ show two different trends. Firstly, a slight reduction in TPLC values are observed for h/δ ranged from 0.1 to 0.25 (values in-between are not reported in figures). Secondly, further increase of h/δ beyond 0.3 results in a significant reduction in TPLC. This is most likely because of increasing h/δ which strengthens the generated vortices and consequently increases the mixing of high momentum fluids with low ones. This process enriches the boundary layer velocity and therefore exhibits more resistance to separate from the suction side. Furthermore, increasing h/δ leads to an increase of the mean stream wise momentum of the boundary layer till h/δ=0.4, nevertheless beyond this value further increase in h/δ has no effect in TPLC reduction. This is due to energizing the lower part of the boundary layer velocity profile, since it is more crucial to reduce the tendency of the flow to separate.
Figure 11 shows the TPLC for the reference case and set E where e/h=4, 5, 6, and 8, while h/δ=0.4, and w/h=6. As shown in Fig. 11, the reduction in TPLC increases from e/h=4 to 5. Further increase in e/h from 5 to 8 leads to a decrease in TPLC. The reason is that the increase of e/h leads to a reduction in bluntness factor, and consequently a reduction in stretching rate and vortex strength. This trend can be attributed to when the parameter “e” increases the BF decreases, on the other hand as “e” increases, “a” increases which can increase or decrease the BF. Therefore, the results show that the reduction gained in TPLC increases by increasing “e/h” up to 5. As e/h becomes larger than 5, the reduction in TPLC decreases due to the weakness of the generated vortices and consequently the reduction in its stretching rate.
Figure 12 shows the TPLC for the reference case and set F with r/δ = 0.25, 0.5, 0.75, and 1.0, where h/δ=0.4, w/h=6, and e/h= 5. It was found that a significant reduction in TPLC occurs with increasing r/δ from 0.25 to 0.5. Further increase of r/δ beyond 0.5 results in a decrease of TPLC. The reason is most probably due to the increase of the bluntness factor which is a correlation on the effect of wing shape on the horseshoe vortex stretching rate developed as reported by Fleming [25]. In rounded nose vortex generator, the parameter “e” affects the blunt nose shape which controls the vortices strength through the bluntness factor “BF” [26,27]. Moreover, as the vortex generator nose radius increases, the time-mean vortex size and strength increase as reported [25]. These strong generated vortices enhance the performance of the compressor cascade till r/δ≈0.5. Further increase in r/δ leads to stronger vortices with larger vortex stretching rate which in turn reduces the enhancement degree [28].
The relationship between Bluntness Factor (BF) and geometrical parameters of vortex generators can be written as:
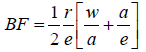 (2)
(2)
where: r is the nose radius, “a” is the distance from the nose head along the CSVG surface to the maximum thickness “w” is the width of vortex generator, and “e” is the length of vortex generator as shown in Figure 4.
Total pressure loss coefficient distribution: The integrated of local total pressure loss coefficient (ζ) distribution is calculated as a function of Z/L by integrating the mass averaged TPLC from y = 0 to y = S for each value of Z/L with a constant Δ Z.
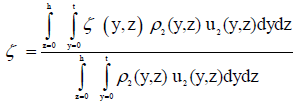 (3)
(3)
where: ζ is defined as the integrated local total pressure loss coefficient, and s is defined as the distance between two blades (pitch).
For sets A, B, C, D, E, and F, the total pressure loss coefficient distribution at the exit plane from the endwall till the midspan is calculated. It was found that for all investigated sets, the mass average of TPLC at Z/L = 0 is approaching unity. The results of sets A, B and C is not reported here. Total pressure loss distribution of sets D, E, and F is reported as shown in Figures 13-15. Figure 13 shows the total pressure loss distribution for set D, at Z/L<0.24, the TPLC is slightly less than the corresponding TPLC for the reference case except at h/δ =0.4, 0.5 where the TPLC is slightly higher than those of the reference case. Whereas at Z/L > 0.32, the TPLC is slightly less than the corresponding TPLC for the reference case except at h/δ=0.1, and 0.15 where the TPLC is slightly higher than those of the reference case.
Figure 14 shows that the TPLC distribution is reduced compared to the reference case along the span for e/h=4, 5, while it’s slightly reduced for e/h=8. For e/h=6 it is reduced at Z/L< 0.06, and increased until Z/ L=0.3, then reduced again. The highest reduction in TPLC occurs at e/ h=5. Figure 15 shows that the TPLC is reduced for all values of r/δ from 0.25 to 1. The highest reduction in TPLC occurs with r/δ=0.5 which is the highest of all sets.
Normalized total pressure loss coefficient: Normalized TPLC is defined as ζn = Δζ/ζRef and it is calculated for all sets by integrating the mass-averaged TPLC value across the exit plane and subtracting it from the integrated mass-averaged TPLC for the reference case. Figure 16 presents the variation of ζn versus h/δ for sets A, B, C, and D. Based on Fig. 16, for set A the ζn reduces by 2.3% at h/δ=0.1. As h/δ increases, the reduction in ζn increases from 3% at h/δ=0.15 to about 5.3% at h/δ=0.4 then decreases to about 3.7% at h/δ=0.5. A Similar trend is observed for set B where ζn is reduced by 1.9% at h/δ=0.1. As h/δ increases, the reduction in ζn increase from 3.25% at h/δ=0.15 to about 6.67% at h/δ=0.4 then decreases 5.82% at h/δ=0.5. For set C, the ζn is reduced by 1.7% at h/δ=0.1. As h/δ increases, the reduction in ζn increase from 3.73% at h/δ=0.15 to about 7% at h/δ=0.4 then decreases to 5.1% at h/δ=0.5. Finally for set D, the ζn is reduced by 1% at h/δ=0.1. As h/δ increases, the reduction in ζn increases from 3.4% at h/δ=0.15 to about 12.6% at h/δ=0.4 then reduced to 5.1% at h/δ=0.5. Figure 17 presents the variation of ζn versus e/h for set E. As shown in Fig. 17, ζn is about 13.4% at e/h=4. As e/h increases, ζn reaches to 18.6% at e/ h=5 and then reduces to about 5.73% at e/h=8. The effect of varying the vortex generator nose radius r/δ on the normalized total pressure loss coefficient is shown in Fig. 18. Based on this Figure 18, ζn is about to 18.62% at r/δ=0. Increasing r/δ to 0.5 results in an increase of ζn to 20.7%, while further increase in r/δ to 1.0 leads to a decrease in ζn to 15.8%. In conclusion, the normalized total pressure loss coefficient can be reached to up 20.7% for set F with r/δ=0.5. This value of 20.7% can be considered the best achievable reduction in a normalized total pressure loss coefficient.
Influence of vortex generators on cascade deflection
Cascade deflection (ε) can be calculated from the following equation:
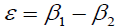 (4)
(4)
where: β1 is the inlet blade angle and β2 is the outlet angle. Figure 19 shows the variation of the percentage of deflection angle Δε/εRef versus h/δ for sets A, B, C, and D. Based on Fig.19, deflection is slightly enhanced for all sets between h/δ=0.1-0.5. However, for set D a significant reduction is observed between h/δ=0.4 and 0.5. As shown in Fig. 19 set E has a slight change in deflection occurring by varying e/h. It is noted that deflection increases by increasing the value of e/h. For set F, as shown in Figure 19 deflection barely changes it’s values range from 0 to -0.5% with r/δ =0.25, 0.5, 0.75, and 1. These results are important for multistage compressors, since the change in deflection angle causes an off design operation for the next stages. However, using vortex generators does not lead to a significant change in deflection and consequently the off-design conditions will still be far from reached.
Influence of vortex generators on static pressure rise coefficient
Static pressure rise coefficient can be calculated from the following:
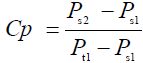
where: Pt1 is the total pressure at the inlet; Ps1 is the static pressure at the inlet; and Ps2is the static pressure at the exit. Fig. 20 shows the variation of the normalized static pressure rise coefficient Cpn=ΔCp/ CpRef at mid span versus h/δ for sets A, B, C, and D. As shown in Fig. 20 Cpn is decreased for all sets, this reduction almost remains constant for set A, while it increases for sets B, C, and D. The percent of change in Cpn has the minimum reduction of 2.7% at set D with h/δ=0.1 and the maximum reduction of -11.6% at set D with h/δ=0.5. For set E, as shown in Figure 20, increasing e/h leads to a decrease in the reduction of Cpn from -12 to -8% as e/h =4, 5, 6, and 8.
For set F, as shown in Figure 20, the reduction in normalized static pressure rise coefficient is almost constant with various r/δ values. This reduction with the increase in total pressure means that there is a considerable increase in the dynamic pressure when using the vortex generators. To benefit from the increase in the dynamic pressure, optimization study can be carried out on the suction blade profile to recover part of the dynamic pressure into static pressure.
Influence of vortex generators on diffusion factor
Blade loading is assessed by the diffusion factor (DF) which relates to the peak velocity on the suction surface of the blade to the velocity at the trailing edge. The diffusion factor can be defined by the following equation [28]:
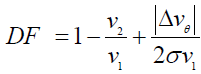 (6)
(6)
where: ν1 is the inlet relative velocity at inlet plane, ν2 is the outlet relative velocity at exit plane, Δνθ is the difference of tangential components of inlet and outlet velocity, and σ is the solidity.
Figure 21 shows the variation of the normalized difference of the diffusion factor DFn (=ΔDF/DFRef) for sets A, B, C, and D versus h/δ at midspan. The diffusion factor is used as an indicator of probability of occurrence in separation. Based on Figure 21, as h/δ increases, the diffusion factor is decreased for all sets except for set C, at h/δ=0.4, and set D at h/δ=0.5 where the diffusion factor is slightly increased. Reduction of the normalized diffusion factor as a percentage varies from 0.5% for set C with h/δ=0.4 to 5.5% for set C with h/δ=0.5. The reduction in the diffusion factor causes a reduction in separation occurrence which may be reflected in the delay or for some sets leading to eliminate separation on the suction surface. For set E, as shown in Figure 21, the diffusion factor reduction is almost constant at -2%. This is also similar to set F, as shown in Figure 21, where the reduction is also constant at -2%. Values of DF in excess of 0.6 are thought to indicate blade stall [24]. In addition, the DF for the reference case is about 0.35.
Figure 21: Normalized diffusion factor for sets A, B, C, D, E and F.
New designs of vortex generators are considered in the current investigation in order to control the secondary flow losses in compressor cascades and therefore enhance the compressor’s performance. Six different sets of vortex generators with varying geometrical parameters and designs are numerically investigated. The flow in the compressor cascade is a 3-d compressible turbulent flow with an inlet Mach number of 0.66 and an inlet angle (β1) of 132°. Numerical simulations are performed using a numerical solver Fluent-14 of the flow through the compressor cascade without and with vortex generators placed on the endwall region near the leading edge of the cascade blade. Considering the current study, some important observations can be made. First, vortex generators have a significant impact on secondary flow losses such as improving the location of separation lines by its moving toward the trailing edge, and reducing the corner vortices. Second, a significant reduction in the normalized total pressure loss of up to 20.7% is accomplished using the curved surface vortex generator with a rounded nose of r/δ=0.5, w/h=6, e/h=5, and h/δ=0.4. Third, using vortex generators results in reduction of the diffusion factor of about -2.0%. This will increase the safe range of operating conditions without stall. Finally applying vortex generators has insignificant effect on the change of deflection and consequently the off design conditions will still be far from reached. However, there is a reduction of static pressure rise which leads to an increase of dynamic pressure. To benefit from the increase in the dynamic pressure, a further investigation is needed to recover part of the dynamic pressure into static pressure.