Enzyme catalysis has been studied as a supportive process in biochemical reactions since the 1800s. The conventional paradigm states that a catalyst accelerates a chemical reaction without affecting its equilibrium) outcome. This notion was formed by decades of analysis of biochemical catalysis under the conditions defined by Henri in 1903, which stipulate that enzyme, substrate and the enzyme-substrate complex are at equilibrium, that a fixed amount of substrate is added at the onset of the reaction, that the substrate concentration is much larger than the enzyme concentration and not affected by the formation of an enzyme-substrate complex (measurement of initial reaction velocity), and that there is no change in enzyme concentration over time. These constraints were developed into the Michaelis-Menten equation (and with the even more restrictive assumption of irreversible reaction steps into the van Slyke equation). They were somewhat released by Briggs and Haldane, who defined quasi-steady state conditions and rephrased these equations to

v=(v_max ⋅ [S])/(k_m+[S])⋅

If [S]<m, then

v=(v_max/k_m) ⋅ [S]=constant ⋅ [Etotal] ⋅ [S],

accounting for incomplete saturation of the enzyme present when only the initial reaction rate is measured. Only at substrate concentrations much above the k_m is the initial velocity of the reaction directly proportional to the enzyme concentration

v=v_max=k_p ⋅ E_total

with k_p=velocity of the conversion from ES to E+P [1]. These formalisms, derived from the Briggs-Haldane conditions, are effectively an artifactual linearization of the complex process of catalysis. It is not reflective of the far-from-equilibrium conditions or the coupled reaction pathways that exist in vivo.

Two prominent characteristics of biochemical reactions taking place in situ are that they occur far from equilibrium and that they are interconnected in non-linear pathways. Homeostasis is distinct from equilibrium, and equilibrium conditions are not compatible with life. Cells are compartmentalized to allow for the formation of concentration gradients. Energy-consuming transport mechanisms exist across compartment barriers to sustain the concentration differences. Biochemical reactions in situ do not produce a mass balance between a fixed amount of substrate and its reaction product, but the substrate input is a function of time. Also, multiple reaction pathways are connected. They are branched at key decision points (e.g. the conversion of pyruvate either to lactate or to acetyl-CoA) to allow for communication among subdomains of the intermediary metabolism (in the pyruvate example, between anaerobic glycolysis and the tricarboxylic acid cycle). Further, In situ biochemical pathways form hypercycles to permit the regulation in hierarchies of feedback loops [2]. Therefore, the study of enzyme catalysis needs to take into account non-steady-state conditions and branched reactions.

Complexity in catalyzed chemical reactions that involve a multitude of reactants has been described. A common laboratory model, the Belusov-Zhabotinski reaction (non-enzymatic, inorganic catalysis by cerium, the reaction proceeds at unphysiologically low pH) can display non- linear behavior [3,4]. In a biological system, glycolysis for ATP generation is a multi-step catalyzed process that may become instable under specific initial conditions [5]. However, whether individual catalysts (enzymes) of single, not coupled reactions have the potential to affect outcome by turning periodic substrate input into non-periodic product generation has been uncertain. Examples were found in the oxidase-peroxidase reaction [6] and a hemin-hydrogenperoxide- sulfite model of catalysis [7], but broad potential for nonlinearity in other enzyme-catalyzed systems has not been established. Enzymatic reactions can be described in general terms by a set of ordinary differential equations for all reactants (Figure 1). Their format has some resemblance to the differential equations describing the Lorenz and Rössler systems of non-linear dynamics [8,9], and therefore implies the potential to generate complex, possibly chaotic behavior.

Figure 1: General enzyme kinetic equations. A) Biochemical notation. B) Differential equations. Commonly k₄ → 0. In the specialized case of substrate inhibition k₂→0. The first term in the differential equation for substrate change assumes rhythmic substrate input in the form of a sine wave.

Here we test the hypothesis that enzyme catalysis can affect the outcome of biochemical reactions. We investigate the parameter space for the rate constants in substrate-activated and general enzyme catalysis, and we study enzyme catalysis in a branched reaction with two competing arms.

In silico modeling

The chemical reactions under study can be defined as sets of ordinary differential equations (ODEs) that describe the rate of change of each reactant per time-step. The solutions of those equations show constant, periodic, or non-periodic flow over time. Here, a solver from a SciPy [10] package (scipy.integrate.odeint) was used to model enzyme catalysis. To solve the equations under study, the time step was set to 0.01 seconds, resulting in a sampling frequency of 100 Hz. The input fluctuated at a constant rate of 0.01 Hz, i.e. each oscillation took 100 seconds or 10000 points. A double precision arithmetic (64 bit) was applied.

Non-linear systems can be represented in a bifurcation diagram as a set of densely packed points. The use of a Fourier transform gives another method of visualization. The Fourier transform is a signal representation in a frequency space. Whereas a signal in the time domain shows how much energy is carried in a given time period, the Fourier spectrum shows how much energy is carried in a given frequency range. The periodicity of a signal is particularly well represented on a Fourier spectrum–as a peak at a specific frequency (and at harmonic frequencies). Because in the chaos regime every period is present, the Fourier spectrum of a chaotic signal has peaks for every frequency.

A bifurcation diagram is a graphical method of presenting a change in a dynamical system depending on a change in one of the underlying parameters. A bifurcation plot represents a map, not a flow (the system is represented by a recurrence, not differential, equation). If a system has only fixed points in some parameter range, this should be represented on the diagram as a solid line. Limit cycles are represented as multiple, vertical lines. The number of lines depends on the period of oscillations. Chaos in this case is represented as a block of densely packed points. To define the reaction states of the enzyme catalysis, we generated bifurcation maps by solving the set of differential equations (Figure 2) for each of its parameters. At every iteration, local minima and maxima values of a chosen variable were plotted on a vertical axis. Upon completion of the desired range of parameters, the resulting graph presents the change of the system’s variables depending on the defined parameter change.

Figure 2: A) Possible reaction scheme for enzyme catalysis with substrate activation (Wang et al. [34]). B) Set of differential equations describing the reaction scheme of substrate activation (E´=E_total–E–ES). The first term in the reaction of substrate change assumes rhythmic substrate input in the form of a sine wave.

Agent-based modeling

For agent-based modeling, a basic NetLogo model on enzyme kinetics was edited to allow for continuous rhythmic substrate input and the visualizations of rate changes (“advanced enzyme kinetics”, program in Netlogo Model Library http://ccl.northwestern.edu/netlogo/models/). The program models the general enzyme kinetic reactions (Figure 1) with each reaction constant (k₁ through k₄), initial substrate volume, and the rate of the driving force (amplitude and frequency) to be set by the investigator.

Cytochrome c reduction assay

The reduction of cytochrome c (type III, from horse heart) by 0.05 mM xanthine and 4 mU/ml xanthine oxidase (grade III, from buttermilk) was determined in 1 ml 50 mM potassium phosphate buffer, pH 7.8, containing 0.1 mM EDTA at room temperature as change in absorbance at 550 nm (calculation of concentration according to the extinction coefficient of 21 000 M^-1cm^-1 [11]). The concentrations of cytochrome c and bovine Cu, Zn-superoxide dismutase were varied systematically. The maximal change in absorbance at equilibrium rather than the initial velocity was determined. Under these conditions, accumulation of hydrogen peroxide and exposure to light could cause reoxidation of cytochrome c [12]. Therefore, 200 U/ml catalase (thymol-free, from beef liver) was present in the assay and the light path remained covered allowing for absorbance readings only in time periods of 2 minutes.

Non-Linearity far from equilibrium

We tested the possibility that an enzyme can alter the outcome of a reaction if it is active far from equilibrium. We first analyzed a case of substrate activation (Figure 2A), because it contains a step of positive feedback that may facilitate instability. This type of reaction is described by a set of differential equations (Figure 2B), where the first term in the change of substrate over time is a rhythmic input reflective of natural changes in substrate supplies that arise in biological systems. The reaction was simulated in silico using Python. Individual calculations of changes in product concentration over time and the Fourier analyses of these traces indicated the possibility of bistabilities and instabilities in these reactions (Figure 3A). We therefore determined the influence of systematic changes in the individual reaction constants and the total enzyme amount present. We generated bifurcation plots for ΔP versus variations in k_n (n=1, 2, 3, or 5) with the other parameters fixed. As shown in Figures 3B and C, this mapping of the parameter space displays ranges of instability that are preceded and succeeded by distinct stable states. Of note, the type of rhythmic input matters to the reaction as the bifurcation plots are very different between sinusoidal and square (on/off) substrate feeds, describing otherwise the same set of differential equations (Figure 4). Hence, in an enzyme reaction with substrate activation that proceeds far from equilibrium, each kinetic parameter and the type of substrate input all have the potential to influence the state of the outcome.

Figure 3a: Individual traces of bistability (left) and chaos (right) in a substrate-activated enzyme reaction. The top panels reflect ΔP (change in product concentration per time interval) over time; the bottom panels display the corresponding Fourier analyses. Y-axis, top panel=label×10^-4, y- axis bottom panel=label×10^-6 (k₁=0.01, k₂=0.1, k₃=14.3, k₄=1, k₅=0.1, E_total=0.5, with sinusoidal substrate input on the left panel and square substrate input on the right panel).

Figure 3b: Bifurcation plots for enzyme catalysis with substrate activation. At their fixed levels, the parameters are k₁=0.01 (varied in top graph), k₂=0.1 (varied in middle graph), k₃=14.3, k₄=1, k₅=0.1 (varied in bottom graph), E_total=0.5.

Figure 3c: Mapping of the parameter space around variations of k₃. Shown are bifurcation plots for ΔP versus variations in k₃ with the other parameters fixed as indicated in the graphs. In A) through C), the substrate input is rhythmic on/off.

Figure 4: Bifurcation plot displaying the effects of different input modes on ΔP versus variations in K₃ for enzyme catalysis with substrate activation. k₁=0.01, k₂=0.1, k₄=1, k₅=0.1, E_total=0.5. The graph for a sinusoidal input 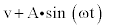with K₃ ranging from 13 through 15 is overlaid on the graph for square input ( 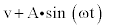alternates between 1 and 0).

The case of substrate activation contains a positive feedback loop. A positive feedback loop induces instability, whereas a negative feedback loop prevents the affected system from being exponentially unstable. A class of oscillatory networks may be defined by the existence of at least one destabilizing and a stabilizing feedback loop. These requirements represent a condition for the occurrence of oscillations [13]. To address whether instability may arise in enzyme catalysis that lacks an autocatalytic step, we also studied a set of general enzyme equations that are more broadly relevant than the case of substrate activation.

Having identified conditions for stability, bistability and chaos in enzyme reactions with the positive feedback mechanism of substrate activation, we applied the same mathematical models to the general enzyme equations (Figure 1). Mapping of the parameter space around the kinetic constant k₃ with bifurcation plots indicated the existence of bistabilities, but provided no evidence for chaos (Figure 5). To gain independent confirmation, we extended this analysis with agent- based modeling using NetLogo [14]. Although no conditions for chaos were found, mapping of the parameter space around the four reaction constants revealed a remarkable role for a non-negligible k₄. k₄ can terminate an enzyme reaction, even if there is a continuous flow of substrate (Figure 6A-C). K₃ is critical for the rate of catalysis (Figure 6D). The influence of k₂ in the range from k₂=0 to k₂=k₁ is minimal (Figure 6B-C).

Figure 5: Mapping of the parameter space around variations of k₃ in the general enzyme equations. Shown are bifurcation plots for ΔP versus variations in k₃ with the other parameters fixed as indicated in the graphs.

Figure 6a: Netlogo models of rates (top panel) and concentrations (bottom panel) of reactants for variations of k₄.

Figure 6b: Netlogo models of reaction rates under variation of k₂ from 0 to k₁ with k₄=0.

Figure 6c: Netlogo models of reaction rates under variation of k₂ from 0 to k₁ with k₄=10.

Figure 6d: Netlogo models of rates (top panel) and concentrations (bottom panel) of reactants for variations of k₃.

Equilibrium shift in competing reactions

Theoretical Basis: In traditional settings, enzymes accelerate the adjustment of the equilibrium in a biochemical reaction without affecting its balance. However, if the catalyzed reaction is one of two possible reactions involving the same substrate, competition for this substrate molecule may cause the enzyme to shift the resulting equilibrium at the end of the reaction. Superoxide anion is very reactive and in vivo can interact with various substrates to form diverse products in competing reactions. For reactions with low turnover rates (such as the spontaneous dismutation) the possibility for diverting superoxide to reactions with other substrates is high. By contrast, the presence of the enzyme superoxide dismutase accelerates the dismutation reaction and diminishes the likelihood of collisions with other substrates that may form distinct products. The equilibrium is shifted in favor of the generation of hydrogen peroxide.

Assume the chemical reactions in the cytochrome c reduction assay where superoxide anion, generated by xanthine and xanthine oxidase, can either reduce cytochrome c or be reduced to hydrogen peroxide by superoxide dismutase (k=reaction constant; the subscripts (+) and (-) indicate the forward or reverse reactions respectively)

k_dismutation=k_dism(+)/k_dism(-)=(- k_reduction(+) ⋅ [cytc(Fe³⁺)]/[H⁺]²)/(-k_reduction(-) ⋅ [O₂] ⋅ [cytc(Fe²⁺)]/[H₂O₂])k_dismutation=k_reduction ⋅ [cytc(Fe³⁺)]/[O₂] ⋅ [cytc(Fe²⁺)] ⋅ [H₂O₂]/[H⁺]²

On the assumption that substrate is in excess and that the reaction is performed in buffer, the equation can be simplified to

k_dismutation=k_reduction ⋅ [H₂O₂]/[cytc(Fe²⁺)]

which indicates that a change in the reaction constant is directly proportional to the change in the ratio of the resulting products in the competing reactions. In general, it holds that

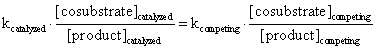
Therefore, the ratio of the products resulting from the competing reactions is proportional to the ratio of the reaction constants multiplied by the co substrate concentrations.

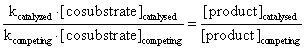
Experimental evidence: The cytochrome c reduction assay provides a versatile model for analysis of the biochemistry of superoxide and superoxide dismutase. The reduction of cytochrome c by xanthine and xanthine oxidase was determined as change in absorbance at 550 nm. The concentrations of cytochrome c and bovine Cu,Zn-superoxide dismutase were varied systematically. In contrast to the classical method [15] the maximal change in absorbance at equilibrium rather than the initial velocity was determined. Under these conditions, accumulation of hydrogen peroxide and exposure to light could cause reoxidation of cytochrome c [12]. Therefore, catalase was present in the assay and the light path remained covered except for readings every 2 minutes.

The xanthine oxidase-catalyzed reaction is complete after circa 14 minutes. On the assumption that xanthine oxidase at pH 7.8 transfers electrons by 30% on a univalent path and 70% on a bivalent path [16], theoretical prediction rates the generation of superoxide anion at 15 nmol and of hydrogen peroxide at 35 nmol. This estimate is confirmed by the spectrophotometric measurements. Figure 7 shows that increasing concentrations of cytochrome c shift the equilibrium of the reaction almost completely toward cytochrome c reduction. In the presence of superoxide dismutase (0.12-0.96 U/ml) this saturation curve is dosedependently lowered. The concentration of ferricytochrome c in the standard assay [15] is 1×10^-5 M. This reacts with about 6 nmol of the 17 nmol O₂^¯ generated. In the presence of 0.12 U/ml superoxide dismutase it is only 4.8 nmol, and after doubling of the superoxide dismutase concentration 3 nmol of cytochrome c are reduced. In conformity to the theoretical calculations, increasing concentrations of superoxide dismutase decrease cytochrome c reduction dose-dependently (Figure 7).

Figure 7: A) chemical reaction for measuring cytochrome c reduction. In the process of converting xanthine to urate, xanthine oxidase generates superoxide anion. In the absence of SOD, superoxide anion reduces cytochrome c (arrow down). In the presence of SOD, the dismutation reaction to hydrogen peroxide is greatly accelerated (arrow up). The addition of superoxide dismutase leads to a competition for superoxide between cytochrome c and SOD. B) Equilibrium of the cytochrome c reduction reaction in the presence (open symbols) or absence (closed symbols) of superoxide dismutase..

Enzymes have commonly been viewed as facilitators, accelerating the formation of an equilibrium that would also form spontaneously, albeit at a lower rate. Here we show that even in a simple competition reaction, the presence or absence of an enzyme affects the resulting equilibrium conditions (Figure 7). The phenomenon can be compared to a flow through a split pipe. The volume flow through each side after the split is proportional to the ratio of the radiuses. The increase in reaction constant, mediated by the addition of an enzyme (over no enzyme), is equivalent to an increase in radius on that part of the split pipe. It leads to a higher substrate flow through the catalyzed reaction.

The ordinary differential equations that describe enzyme catalysis imply the possibility of bistability, and-in the case of substrate activation-of chaos in the rate of product generation (Figures 3 and 5). Of note, the general enzyme equation investigated here is of the most basic form that describes the conversion of one substrate into a product (Figure 1). Further studies are required to determine whether reactions with two substrates may give rise to non-linearity. Experimental observations have demonstrated earlier that coupled enzymatic reactions can - under certain conditions - display complex behavior ranging from birythmicity to chaos [5,17,18]. Bursting pH oscillations were found in the hemin-hydrogen-peroxide–sulfite model of catalysis [7], where hemin is believed to represent the reaction mechanisms mediated by heme-containing enzymes [19]. On the individual enzyme level, the oxidase-peroxidase reaction has displayed complex behavior [6,20], and mapping of the parameter space in bifurcation diagrams has revealed the possibility of chaos [21-23]. The brain tyrosine and tryptophan hydroxylase systems can display non-linear behavior for certain ratios of their substrates [24]. However, the underlying models involve more variables and are less generally applicable than the equations investigated here. Our models provide a theoretical basis to explain non-linear phenomena, and they characterize enzymes in their physiological context of far-from equilibrium, branched reactions.

The traditional spectrophotometric analysis of enzyme kinetics is largely limited to Michaelis-Menten or Briggs-Haldane conditions. The study of far-from-equilibrium states is effectively accomplished with mathematical modeling, which also has the advantage of providing general answers without being constrained to one particular enzyme. A technique we have employed here is the mapping of the parameter space for the enzyme kinetic constants using bifurcation diagrams. The application of graphical approaches to study biological systems can provide insights for the analysis of complicated relations, as demonstrated by many previous studies on related biological topics, such as enzyme-catalyzed reactions [25-28], enzyme inhibition [29], and drug metabolism systems [30].

There has been a gap between the observation that enzymes can have dramatic effects in vivo, when given therapeutically or when absent due to inborn errors of metabolism, and the biochemical dogma that catalysts accelerate the equilibrium but do not change the result of a chemical reaction. Our study has implications for the assessment of enzyme efficacy and toxicity when used in therapy. Like all drug compounds, enzymes have limited dose windows of efficacy, below which they are ineffective and above which they display adverse effects. For superoxide, an enzyme used in this study, the loss of protection from free radical damage at high doses was documented about 30 years ago [31,32]. Various explanations, such as over-scavenging of superoxide, were put forward [33,34]. The present analysis shows that state changes far from equilibrium or competitions in non-linear reaction pathways may provide valid explanations for such phenomena.

Historically, the reductionist approach has been tremendously successful in research. Yet, key accomplishments within this framework (such as Newton’s mechanics in physics and Henri- Michaelis-Menten kinetics in biochemistry) have generated progress in insight at the expense of idealizing the systems under study to provide essentially linear models. These models disregard complexity, even though a nonlinear progression of events is much more common in nature than a linear one. Since Newton’s mechanics (developed in 1687), physics has expanded to thermodynamics, quantum mechanics and non-linear systems dynamics. As shown here, the set of ordinary differential equations that describes enzyme kinetics in general terms, and in the case of substrate activation, allows for a much broader spectrum of outcomes than can be obtained under the conventional laboratory conditions defined by Henri, Michaelis and Menten or Briggs and Haldane (published in 1925). It is inevitable to recognize the complex potential of enzyme catalysis and to expand enzymology beyond the conventional, linear models.

GFW is supported by DOD grants PR094070 and BC095225. We thank the Santa Fe Institute Complex Systems Summer School for stimulating discussions.