Forest Research: Open Access
Open Access
ISSN: 2168-9776
+44 1300 500008
ISSN: 2168-9776
+44 1300 500008
Research Article - (2014) Volume 3, Issue 2
The measurement of above-ground biomass is important to understand carbon flow between trees and the atmosphere; remote sensing plays an important role in making this possible for extensive and hard-to-reach areas. This study compared above-ground forest biomass estimation models using data from different sources, including Landsat ETM ster GDEM, ALS (LiDAR) and forest inventories. Two sets of predictors were established: the first included variables extracted from Landsat ETM and Aster GDEM, while the second included variables from Landsat in combination with LiDAR products (Digital Terrain Model, Digital Surface Model and Canopy Height Model). The Random Forest algorithm was used to build all models; this method explicitly returns the importance of each predictor and therefore allows the selection of the best set of variables. Estimations were made separately by forest cover for Pinus radiata, Eucalyptus globulus and second-growth Nothofagus glauca. Better results were obtained using the combination Landsat-LiDAR than those using Landsat-Aster GDEM data. Also, the results were better when applying the model to pine cover (pseudo R2 77.22%).
<Keywords: Above-ground biomass; Landsat ETM+; LiDAR; Random forest.
The study of forests is a growing area of research due to their importance in different natural processes; the carbon cycle is one of the main processes. This is due to the fact that terrestrial ecosystems are the greatest contributors to the global carbon balance [1]; they contain close to 60% of the carbon stored in vegetation and 50% of that stored in the soil [2]. Carbon in forests may be divided into three components: biomass in living plants; plant remains and soil [3].
Most studies related to carbon content in forests are performed on the above-ground biomass, defined as the weight or equivalent estimation of organic material growing above the ground [4]; the different methods of estimating this content may be classified by the type of information they utilize.
The method most used to estimate above-ground forest biomass is that of forest inventories. These use allometric equations which relate easily-measured field data such as tree height and diameter at breast height (DBH) with above-ground biomass [5]. Although this is the most precise method it has greater cost, especially when it is desired to estimate biomass in extensive or hard-to-reach zones. Given the operational difficulties, methods have been developed which combine inventories with information acquired by remote sensing [6,7] and environmental variables (i.e. slope, exposition, altitude and ground curvature) [8].
Passive remote sensors use solar energy to obtain spectral information about objects. Among the most used are the mediumresolution multispectral satellites Landsat ETM+ and Aster (30 and 15 meters, respectively) [9]. The information provided by these sensors allows relating reflectance, vegetation indices and/or transformations of different spectral bands to above-ground biomass. One of the advantages of using these images is that some of them may be acquired free or at low cost. The same is true for the Digital Elevation Models (DEM), SRTM (“Shuttle Radar Topography Mission”) and Aster GDEM (Aster “Global Digital Elevation Model”), from which it is possible to derive topographic information to be correlated with aboveground biomass [10,11].
LiDAR (“Light Detection and Ranging”) is an active remote sensor that obtains a cloud of points with X,Y, and Z coordinates which provide information about the structure of objects on the ground [12]. Measurements are obtained by estimating the distance between the sensor and its objective by the time between the emission and return of a laser pulse [13]. Data of this type have been used by various authors [14-16] to obtain metrics or high-resolution models related to forest heights. One of the models most used is that of Digital Surface Models (DSM), which represent the surface of the Earth including all objects on it, and the Canopy Height Model (CHM), which estimates the height of the trees. One of the main difficulties and disadvantages of this type of data, compared to multi-spectral images, is the high cost of acquiring and processing them.
There are two major types of statistical models, those which focus on the data and those which focus on algorithms [17]. The focus based on the data begins by assuming a stochastic model such as linear or logistic regression, whose fit is used both to predict responses (Y) to future data (X) and to extract information about the nature of the relation between variables X and Y. The approach based on algorithms focuses on prediction and uses estimations of its exactitude to validate the models, without considering the type of relation between the variables. The latter approach is generally called machine-learning models.
In the construction of statistical models for the estimation of aboveground biomass both approaches have been used. Initially techniques were employed such as multiple regression, k-NN classification and neural networks [18] on data from active and/or passive sensors. However, in recent years the use of machine-learning type algorithms based on classification and regression trees has increased. Among these, the Random Forest regression has been used to estimate forest parameters [10,19-22], with better results than other methods.
About 22% of the surface area of continental Chile (16.6 million ha) is covered with native forests and forest plantations, concentrated mainly in the central part [23]. This makes the country an interesting place for biomass studies, to estimate the capacity for carbon storage, to implement management measures or to estimate the potential production of biofuel.
The objective of this study is to compare models of above-ground forest biomass estimation, combining satellite information obtained from the Landsat ETM+ sensor, Aster elevation data, information derived from LiDAR point clouds and field measurements.
Test site
The study area is an experimental forest property of the Universidad de Chile named Pantanillos, located in central Chile (Figure 1), between coordinates UTM (WGS84) 744187 – 746042 meters east and 6074000 – 6070800 meters north.
Pantanillos has a surface area of approximately 400 ha, the majority of which is covered with plantations of Pinus radiata D. Don and in lesser quantity of Eucalyptus globulus Labill. It also has sectors of second-growth native forest, in which hualo (Nothofagus glauca Phil. Krasser) is the predominant species.
Field reference data
Field data were compiled in February, 2011, by establishing a systematic net of conglomerates every 200 m. Each conglomerate was formed by five sampling subunits, one central and four at 30 m distance in each of the cardinal directions. Each subunit consisted of concentric circular plots of 2, 4 and 8 m radius, which included trees with DBH ≥ 5, 10 and 20 cm, respectively (Figure 1). The following state variables were recorded in each plot: DBH (cm), species, total height (m), and other complementary descriptors. A total of 83 conglomerates were measured which encompass 330 plots (some plots were missing due to accessibility issues).
Estimation of the above-ground biomass with field data
The following allometric functions were used to estimate the aboveground biomass of individual trees:
E. globulus [24]:
BA = −92 + 2.3* LN(DBH) (1)
P. radiata [25]:
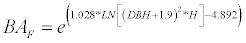 (2)
(2)
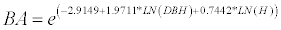 (3)
(3)
BA is the total above-ground biomass (kg), BAF is stem biomass (kg), DBH (cm) and H is height (m).
For radiata pine BAF is the above-ground biomass of the stem with bark; thus it was necessary to add the above-ground biomass component of branches and needles (non-stem biomass). This was done using the component equations of Corvalán and Hernández [27] for the percentage of stem above-ground biomass (BF%) and that of the non-stem biomass (BNF%).
The final equation for the stem above-ground biomass (BF%) was:
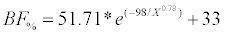 (4)
(4)
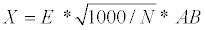 (5)
(5)
Where X is the mean distance between trees, E is the age of the stand, AB is the basal area and N is the number of trees. Finally, BNF% was calculated as the complement of the stem biomass area, assuming a constant bark biomass of 10%.
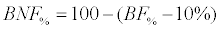 (6)
(6)
Total above-ground biomass per hectare in each plot was calculated by summing the individual stem biomass of each tree multiplied by its respective expansion factor, plus the non-stem biomass expressed as an aggregate function of total stem biomass divided by total biomass.
Processing of satellite images
We obtained two Landsat ETM+ scenes from 8 December 2010 and 9 January 2011 (Path/row 233/85). Both images were rectified by polynomial functions using the UTM projection (WGS84 zone 18 south).
A radiometric correction was performed by conversion of Digital Number (DN) to radiance using the specific gain and offset of the sensor. We then applied an atmospheric correction using the method of Dark Object Subtraction proposed by Chávez [28], and a topographic correction using the method of Civco [29]. Reflectance was obtained by applying a simplified model with the correction parameters of Chuvieco [30]. Since the images were taken after 2003, that is, they contain the SLC-off error, both images were fused using the method of Scaramuzza et al. [31] (Figure 2). The reflectance bands were also used to obtain the Tasseled Cap transformation [32] and the vegetation indices shown in Table 1.
| Index | Equation | Reference |
|---|---|---|
| Difference Vegetation Index (DVI) | 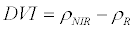 |
Roujean and Breon [33] |
| Simple Ratio (SR) | 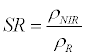 |
Jordan [34] |
| Red Green Ratio (RGR) | 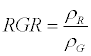 |
Gamon and Surfus [35] |
| Red Green Index (RGI) | 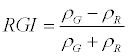 |
Coops et al. [36] |
| Normalized Difference Vegetation Index (NDVI) | 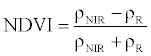 |
Rouse et al. [37] |
| Corrected Normalized Difference Vegetation Index (NDVIc) | 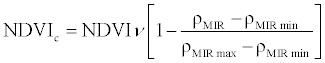 |
Nemani et al. [38] |
ρNIR = Near Infrared, ρR = Red, ρG = Green, ρMIR = Middle Infrared.
Table 1: Vegetation Indices utilized in the study.
Processing of the aster elevation digital model
We obtained the free Aster GDEM Elevation Digital Model from the web site of the same name, with a spatial resolution of approximately 30 meters. From this we obtained topographical variables of aspect (in azimuth degrees), slope (in percentage) and land curvature (concave, convex or flat).
Processing of LiDAR data
LiDAR data were obtained in March 2011 with a mean density of the point cloud of 5 points per m2, and a true three-band ortho image (visible RGB) with a spatial resolution of 0.5 m.
As a first step to obtain the Digital Terrain Model (DTM) from the LiDAR, we used the multi-scale curvature algorithm to identify the points at ground level [39]. The points not classified as ground were interpolated to obtain a Digital Surface Model (DSM) [40]. We also obtained a Canopy Height Model (CHM) as the difference between DTM and DSM, which shows the tree heights. The three models (DTM, DSM and CHM) were obtained at a spatial resolution of 1 m. As with the Aster GDEM, from the LiDAR DTM we obtained the topographic variables elevation, slope, aspect and land curvature.
Parceling
Parceling consisted in the identification of homogeneous units according to the dominant vegetation present. This was done by photo interpretation of the true ortho image complemented with field data. We identified 5 types of vegetation cover: P. radiata plantations, E. globulus plantations, second-growth native forests, mixtures of forest covers and a class called other, which included bare areas, buildings and areas outside the forest property.
Estimation of above-ground biomass
We used the method based on classification and regression trees called Random Forest (RF), available in the statistical software R-Project [41], under the name random forest package. This algorithm, proposed by Breiman [42], constructs a tree of classification or regression using a process called bagging (“Bootstrap + Aggregation”) [43,44]. In RF each node is separated using the best division chosen among a subset of randomly chosen predictor variables. This algorithm produces an internal error estimation, thus the results do not require cross-validation or independent validation [45].The error of estimation is calculated by leaving out of the bootstrap sample about one third of the reference cases not used in the construction of the tree. These data are so-called “out-of-bag” (OOB), and are predicted using the tree created by the bootstrap sample. On the average each datum is an OOB about 1/3 of the time; these predictions are averaged and the mean square error (MSE) is calculated [46].
RF provides a pseudo R2 similar to the R2 of a standard linear regression; it is called pseudo because it uses the values predicted by RF to calculate the MSE. Pseudo R2 may take negative values, which are interpreted as very poor fits [47]. RF also calculates the relevance of the predictor variables, assigning a score that depends on the changes in the error when the values of this variable are permuted (called %IncMSE); if the effect is larger the variable is assigned greater importance [48].
We estimated above-ground biomass for P. radiata, E. globulus and second-growth native forest separately. Since RF includes an element of randomness, each estimation was repeated 100 times. To evaluate the sources of information, the root mean square error (RMSE) (equation 7) and percentage RMSE (equation) were calculated from the MSE returned by RF.
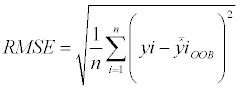 (7)
(7)
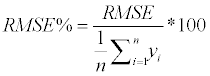 (8)
(8)
Where the yi are the observed data.
Variables were extracted based on a point cloud established every 30 m, in which were also included the coordinates of each point and the point above-ground biomass calculated with field data when available. For the variables obtained with LiDAR data the extraction was performed based on an area of influence of 8 m radius based on the net of points, obtaining the mean value for the area. In the extraction of DCM and DSM the standard deviation was also estimated.
To compare the capacity of Landsat, Aster GDEM and LiDAR to estimate above-ground biomass, two sets of predictors which occupy combined sources of information were used (Table 2).
| Landsat +GDEM Set | Landsat+LiDAR Set |
|---|---|
| Landsat: Reflectivity (TM1 - TM5 y TM7) Vegetation Index Tasseled Cap (TC1-TC6) |
Landsat: Reflectivity (TM1 - TM5 y TM7) Vegetation Index Tasseled Cap (TC1-TC6) |
| GDEM: Elevation (E) Slope (S) Aspect (Asp) Curvature (C) |
LiDAR: Elevation (Li_E) Slope (Li_S) Aspect (Li_Asp) Curvature (Li_C) |
| DSM (Li_DSM) Standard deviation DSM (Li_DSM_sd) CHM (Li_CHM) Standard deviation CHM (Li_CHM_sd) |
Table 2: Sets of predictors used in the estimation of aboveground biomass.
With the Landsat + GDEM set using all the predictors the best fit was obtained in pine plantations, 56.02%. However, for eucalyptus and second-growth native forest the pseudo R2 were low, with values of -5.73% and 2.5%, respectively. The selection of variables improved the fit and decreased the error (Table 3).The estimations in P. radiata and second-growth hualo selected variables related to topography and the spectral response, while in E. globulus only three predictors derived from Landsat were selected (Figure 3a).
| PR | EG | NG | ||
| Landsat + GDEM |
Pseudo R2 | 60.26 (± 0.55) | 37.84 (± 2.19) | 7.76 (± 1.24) |
| RMSE | 44.58 (± 0.31) | 25.81 (± 0.83) | 55.2 (± 0.37) | |
| RMSE% | 51.59 (± 0.32) | 60.83 (± 1.95) | 75.24 (± 0.51) | |
| Landsat + LiDAR |
Pseudo R2 | 77.22 (± 0.37) | 37.92 (± 1.78) | 30.95 (± 1.05) |
| RMSE | 33.75 (± 0.27) | 25.79 (± 0.37) | 47.76 (± 0.37) | |
| RMSE% | 35.40 (± 0.28) | 60.79 (± 0.87) | 65.09 (± 0.50) |
PR= Pinus radiata, EG= Eucalyptus globulus and NG= Nothofagus glauca.
Table 3: Fits and mean errors for estimations with selection of variables for the two proposed sets of predictors.
Figure 3: The graphs show the order of importance of the variables obtained in RF for the Landsat + GDEM and Landsat + LiDAR sets according to the dominant species. Red bars indicate the variables selected for the second estimation. PR= Pinus radiata, EG= Eucalyptus globulus and NG= Nothofagus glauca (native forest).
In estimations using Landsat and LiDAR the fit values increased for P. radiata (pseudo R2=75.72%) and second-growth hualo (pseudo R2=13.90%) compared to those obtained using Landsat + GDEM, while E. globulus continued with negative pseudo R2 (pseudo R2=-0.92%). With selection of variables the fit in P. radiata was improved using variables of Landsat and LiDAR. For E. globulus a fit of only 37.92% was achieved (similar to that of Landsat + GDEM with selection of predictors) in which the variables of canopy structure were not relevant, in contrast to the estimations in second-growth hualo, in which only this class of variables was selected (Figure 3b).
The set of predictors which used variables from Landsat and GDEM produced poorer fits than the second set, which incorporated information related to canopy height extracted from the LiDAR point cloud. These results concur with those of Lefsky et al. [49], who indicated that the metrics of canopy structure, mainly height and its standard deviation are highly correlated with the above-ground biomass of forests. Latifi et al. [19] also found this relation using a genetic algorithm for variable selection, although they also used other predictors extracted directly from the point cloud such as height percentiles.
In the estimations of pine and eucalyptus plantations and a second-growth native forest, both the fits and the type of predictors selected were considerably different for the two sets of predictors. The differences in fit among the three vegetation types may be due both to their horizontal and vertical structures. In pine plantations the horizontal structure is more homogeneous than in areas with native forest, which have not only a more complex and irregular canopy geometry but are also less dense. Clark et al. [50] found that plantations had higher correlations with metrics from LiDAR than forests with irregular structure. Our results agree with those of Popescu et al. [51], who obtained fits of 0.33 for deciduous forests (RMSE 44 ton/ha) and 0.82 for pine (RMSE 29 ton/ha), similar to our results.
Although eucalyptus plantations are homogeneous horizontally, the vertical structure of individual trees produced a large difference in the results. In pine plantations, the canopy structure allows a greater proportion of points to be intercepted in the canopy, which allows the creation of more precise models of the canopy surface, and thus also more precise DCM. On the contrary, in eucalyptus plantations trees are less leafy and canopies are sparser, thus many more points do not fall in the canopy of the trees but rather in the ground or the undergrowth, thus the DSM and DCM are less precise. LiDAR point clouds with higher densities may be suitable to compensate this problem but computing cost may also rise.
We conclude that the use of data which include information related to the canopy structure, such as the Digital Surface Models and Digital Canopy Models, produced better results (greater correlations) and lower errors. This was true in the estimations of pine and secondgrowth native forest but not for the estimations in E. globulus.
The differences in the fits of the estimations may be due to the precision obtained in the canopy models, given the vertical structure present in the different kinds of cover evaluated. In the estimations for E. globulus the utilization of LiDAR data did not improve the fit, which may indicate that the point density (5 points/m2) is not dense enough to represent correctly the tree canopies, sub-estimating the height of the stand.
This study estimated biomass using digital models related to canopy height, which estimates the mean height of the vegetation in each pixel. However, it is also possible to use other variables extracted directly from the LiDAR cloud points which may reveal the structure of other strata (such as understory); using these variables could improve the fits estimations.
This study was financed by the BIOCOMSA Consortium (CORFO-INNOVA) as part of their project “Evaluation and monitoring of existing Aerial Biomass and optimization of supply networks to biofuel plants. We also thank the Laboratorio de Geomática y Ecología del Paisaje (GEP) of the Universidad de Chile.