A rich phase diagram containing a hierarchy of structures manifested at different length and time scales is the signature of colloidal gel which is a unique state of soft matter [1-9]. Gelation and their arrested phases have been well studied in the literature in the past [1-13]. Multiple arrested phase states can be best followed, and hence probed using colloidal clay dispersions as model systems. The anisotropy associated with the geometrical shape and charge distribution in clays like laponite attributes unique properties to their dispersions. For instance, such systems contain both attractive and repulsive potentials in their interactions that allow either the system to form gel or to form a glassy phase. An interesting feature of clay suspension is the existence of interactions at different length and time scales which lead to a variety of structural and dynamical phenomena occurring as function of clay concentration and of the ionic strength. Recent studies performed on laponite dispersions have unveiled clear understanding of aggregation and glass formation which has further led to the unambiguous description of dynamical arrest and viscoelastic phase separation [9,10]. The gelation of dispersions of clay particles is both industrially important, as well as scientifically challenging [11,12]. In general, gels have found applications in drilling fluids, paints, varnishes and in cosmetic and pharmaceutical formulations. In addition, clay-polymer nanocomposites with customized properties could be successfully made [13].Thus, it is imperative to consider new clay based soft matter systems that can widen the potential of their applications to newer domains.

Clays like laponite are discotic platelets with fixed aspect ratio (30, diameter ≈ 30 nm thickness ≈ 1 nm) and surface charge density (zeta potential ≈ -35 mV), and their dispersions exhibit an array of soft matter phases that evolve with waiting time as well as solid concentration. Laponite is known to exhibit significant age dependent dynamics in aqueous dispersions [7-12]. Similarly, the salt dependent phase states of this clay have been reported extensively in the literature.In the recent times there has been a lot interest in room temperature ionic liquids. Ionic liquids (ILs) are salts composed of poorly coordinating organic cations and inorganic anions which are liquid below the boiling point of water. They possess appealing features such as low melting point, negligible vapor pressure, non-volatility, no-flammability, wide electrochemical windows and so on [14-26]. ILs are often referred to as “designed solvents” because their physical properties could be tailored by adjusting the structures and species of the constituting cations and/ or anions [19]. The variety of possible combinations of ILs with laponite can, in principle, generate a wide spectrum of designer soft materials. These can be used as filling material and matrices to tailor requirement based personal care, pharmaceutical and other industrial products.

Gels prepared in ionic liquid environment (ionogels) display unusual properties [27-36]. In ionic liquid (IL) solutions, one introduces mobile ions (in the form of mobile anions and comparatively heavy cations), hydrophobicity (alkyl chain length) and hydrogen bonding (N---H) possibility simultaneously into the continuous phase. These liquids, comprising of organic ions, are associated with negligible vapor pressure, high thermal, chemical and electrochemical stability that enable these to be treated as green solvents [37]. There exist several examples of ionogels depicting unusual properties. Preparation and microscopic dynamics of ionogels exhibiting two glass transition temperatures, which drastically decrease as the ionic liquid content increased due to increased plasticization of the polymer, was studied and has been reported [31,32].

In this work, we explore the gelation kinetics of laponite dispersions made in ionic liquid solutions in a systematic and comprehensive manner in a bid to establish their structure-property relationship. Further, the study was extended to probe the temporal relaxation dynamics of concentration fluctuations through the measurement of dynamic structure factor. The following protocol was used to achieve the above mentioned objective. The laponite dispersions were prepared and ionic liquid was added to this preparation to evaluate their influence on temporal effects of re-organisation self assembly, gelation kinetics and relaxation dynamics.

We have performed a systematic and comprehensive study to establish the time dependent formation of gel phase of laponite dispersions in ionic liquid (IL), 1-Ethyl-3-methyl imidazolium chloride, solutions at room temperature. Self-assembly of IL coated laponite platelets preceded gelation. Considering the fact that this particular nanoclay, in its gel form, has found applications in pharmacy, food, and cosmetic industry etc. modifying its thermal and rheological properties is called for.

The IL, 1-ethyl-3-methyl imidazolium chloride, was bought from Sigma-Aldrich and was used as received. Deionized water from Organo Biotech Laboratories, India, was used to prepare the solutions. Laponite RD clay was purchased from Southern Clay Products, USA. We dried the laponite powder for 4 hrs at 120°C to remove its moisture content. IL solution was prepared by dissolving IL in double distilled deionized water for an hour. Laponite dispersions (2% w/v) were prepared by dispersing Laponite into double distilled deionized water and stir for 2 hours [19]. The desired IL concentration was achieved by adding a concentrated stock of IL solution. The pH of Laponite dispersion was adjusted to 10. All dispersions appeared optically clear and transparent. The concentration of laponite was maintained fixed at 2% (w/v) and the IL concentration was varied from [IL] = 0.01 to 0.05% (w/v). All preparations were made at room temperature 20º C and the relative humidity in the room was less than 50%. All the concentrations are in % (w/v) unless otherwise stated.

Dynamic light scattering (DLS) experiments were performed on a 256-channel digital correlator (Photocor Instruments, USA) that was operated in the multi-tau mode (logarithmically spaced channels). The time scale spanned over eight decades, i.e. from 0.5 μs to 10s. This instrument used a 35mW linearly polarized He-Ne laser. A Glan Thomson analyzer was used in front of the photomultiplier tube to enable collection of polarized components of scattered light. The scattered intensity values were measured for 20º <θ< 150º. The probe length scale is defined by the inverse of the modulus of the scattering wave vector q where the wave vector q = (4πn/λ) sin (θ/2), the medium refractive index is n, excitation wavelength is λ (= 654 nm) and θ is scattering angle. Further details on dynamic light scattering can be obtained from ref [20].

Light scattering analysis

Dynamic light scattering (DLS) probing was used to study time dependent fluctuations of light scattered from laponite dispersion containing Ionic liquid (IL). In order to observe the effect of ionic liquid (IL) concentrationon the aging dynamics of 2% laponite dispersion we performed dynamic light scattering measurements. Here, we measured the polarized (VV) intensity correlation functions independently at different scattering angles 20º <θ< 150º that allowed probing the sample over various length scales. The polarized autocorrelation function g1(q,t) gives information on the translational diffusion coefficient. The dynamic structure factor or electric field correlation function g1(q,t) could be described as sum of exponential term and Kohlrausch- Williams-Watts (KWW) stretched exponential function given as [38]

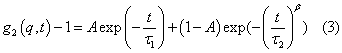
where the exponential term describes fast relaxation with characteristic time τ₁ whereas the stretched exponential term which is governed by characteristic time τ₂ and stretching parameter β describes slow relaxation. A and (1-A) are the weights of the two contributions. For an ergodic scatterers, i.e. 0 ≤ g1(q,t) ≤ 1 and at t→∞, the correlation function relaxes to a value equal to zero (baseline). In non-ergodic systems, the scatterer is dynamically arrested and is unable to probe the entire phase space. As a consequence, the g1(q,t) at t → ∞ cannot relax to its limiting value, but remains frozen at value greater than 0. The deviation of the baseline from the fully relaxed state is a measure of non ergodicity present in the system (defined as h_vv).

Figure 1 illustrate the polarized correlation function g1(q,t) data for measurements pertaining to θ = 90° for samples containing various amount of IL in the dispersion. The effect of aging is clearly visualised in this data. The observation can be clearly made from this data. The correlation function did not fully relax with aging time of the samples implying the emergence of non-ergodicity in the samples.

Figure 1: Waiting time evolution of normalized polarized autocorrelation function measured at an angle 90º for 2% (w/v) laponite with (a) 0% (b) 0.01%(c) 0.03% and (d) 0.05% (w/v) [IL]. The solid lines represent fits to equation (1).

Figure 1 shows the waiting time evolution of polarized autocorrelation function at scattering angle 90° and indicate that all the system undergo transition from ergodic to non ergodic state. The system undergo transition from sol to gel state can be visually confirmed by titling the vials filled of samples and observing that the samples doesn’t flow after a certain time and second through the decay of correlation function which doesn’t undergo fully decay as system is undergoing transition from sol to gel state. The measurement times was varied from 9 hr to 18hr depending on the concentration so that accurate correlations functions are measured during the sol to gel transition process. For pure laponite, we can see that with increase in waiting time, g₁(t) did not completely relax which indicate the confinement of laponite platelets in arrested phase. On introducing IL into the Laponite dispersion the system undergo earlier transition as compared to pure Laponite. On comparing the decay of correlation function of Laponite- IL dispersion we observethat the samples exihibited non-ergodicity much earlier above 0.03% as compared to low concentration. Thus, we conclude that with the increase in concentration of [IL] in laponite dispersion, the system developed non ergodic phase rather quickly as compared to pure laponite dispersion. Thus, introducing IL into the Laponite dispersion enhances the transition to non-ergodic state.

From the correlation function also we classified our samples into two gels. The decay of correlation function for higher IL concentration is earlier and also the difference is much less. The decay of correlation function varies from 1 to approximately 0.88 which led us to conclude that above 0.03% (w/v) IL concentration the gels formed are fragile. From time dependence behaviour of Laponite-IL we can say that above 0.03% (w/v) the gels formed are soft as compared to below this IL concentration.

We now have a look at the behavior of stretching exponent (β) which characterized the broadness of the distribution of slow relaxation mode contributing to the correlation function. In figure 2 the behavior of stretching parameter (β) which characterized the broadness of the distribution of slow mode contributing to the correlation function as the function of waiting time (tw) is shown for samples with [IL] concentration 0% 0.01%, 0.03% and 0.05% (w/v) and it was found that the value of stretching parameter decreased with time from a value of ~0.7 to an extremely low value ~ 0.01 in the case of 0%, 0.01% and 0.03% (w/v) IL samples which implies that at higher waiting times the correlation functions become more and more stretched. However, decrease in case of 0.05% (w/v) is also seen but it is very small because above 0.03% the samples undergo much earlier transition as compared to others. The decrease in stretching parameter with waiting time implies that as the waiting time increases, the system is reaching to arrested state i.e transition from ergodic to non ergodic takes place. This decrease in stretching parameter shows that the dynamical properties of the sample change with waiting time and the structural rearrangement inside the sample during the transition from ergodic to an arrested non ergodic state has been observed. However, the variationof stretch exponent β remains independent of wave vector (q) for different IL concentration.

Figure 2: (a) A plot of stretching exponent as a function of waiting time for different angles with 2% laponite and different concentration of [IL]. (b) Value of gvv1(t) at long delay time say hvv as a function of waiting time for laponite with different concentration of [IL].

It is impossible to determine transition from ergodic to non ergodic in the system because of low signal modulation, thus the value of g₁(t) at long delay time (t → ∞ ) abbreviated as h_vv for polarized mode. This hvv value provides quantitative estimation of ergodicity and non ergodicity. This value of g₁(q,t)at t → ∞ which defines the degree of non–ergodicity (h_vv parameter) increases with aging time for all the samples. For fully ergodic systems it assumes a value of 0 whereas for a completely non ergodic system it has a value approximately equal to1. Figure 2(b) shows variation of h_vv as a function of waiting time for different concentration of [C2mim][Cl] i.e.0 , 0.01, 0.03 and 0.05% (w/v),respectively, in which increase in hvv value is observed.

The sharp change in value of the stretching exponent (β) and h_vv value with waiting time gives us the ergodicity breaking time (t_EB). The variation of ergodicity breaking time calculated from both the parameter of Figure 2 is shown in Figure 3.The aging time at which there is sharp change correspond to ergodic –nonergodic transition. Higher concentration of IL i.e>0.03% (w/v) take less time as compared to low concentration to get arrested. From Figure 3 also we can demarcate two regions one below 0.03% where structured gels are formed and other above 0.03% IL where fragile gels are formed.

Figure 3: Value of ergodicity breaking time (tEB) as a function of [IL] concentration from hvv and stretching exponent analysis. The verticle lines represent the error bars.

Next we study the angular dependence of the scattering function g1(q,t) shown in Figure 1. The correlation function were measured at different angles changing the scattering wave vector in the range 0.006< q < 0.0231 nm-1(30º <θ< 130º). The relaxation time τ₁ and τ₂ were obtained from the analysis of correlation functions.

However, observing their angular dependence we found that τ₁varies as q^-2seen from Figure 4 (a). The q^-2 dependence of τ₁ led us to conclude the diffusive nature of fast mode relaxation time. On observing the behaviour of τ₂, it was also found to scale as q^-2. Thus the variation of relaxation time as q^-2 confirms the diffusive nature in our system (Figure 4b).

Figure 4: Plot of q dependence of (a) fast relaxation time (τ₁) and (b) slow relaxation time (τ₂) for 2% (w/v) laponite with different [IL] concentration ( t = 0). Representative error is shown.

To further investigate the characteristics of the slow mode, the time dependence of the relaxation rate of the fast and slow mode was determined. The behavior of slow mode relaxation time τ₂ for polarized correlation function is shown in Figure 5 as a function of waiting time in a logarithmic plot for our [IL] samples. From these we observed increase in slow mode relaxation time with increase in waiting time. The slow mode decay time of correlation function provide information for the time a particle needs to forget its initial position. From the figure representing the time dependence of slow relaxation rate, two distinct regions are evident where τ₂ progressively increased with waiting time initially and after certain time it become nearly constant. The increase in relaxation time τ₂ with waiting time implies that very rapidly the aging freezes in a certain degree of system. The increase shows the exponential behaviour in one region and linear in second region.

Figure 5: Evolution of the fast and slow relaxation timeas function of waiting time, tw for samples with 2% (w/v) laponite and different IL concentration.

The relaxation time τ₁ correspond to fast relaxation mode was found to increase with aging time. The selective binding of polar head groups of monomeric and oligomeric IL molecules to negatively charged faces of laponite platelets dominates over the other usual interactions. The degree of charge neutralization thus achieved combined with the favourable hydrophobic interactions facilitated the gelation and arrest kinetics. The matured arrested phase was found to be gels in responses to dilution. The coherent picture that emerged was that IL molecules due to their large polar head groups and short hydrophobic tails are capable of exfoliating the colloidal dispersions and hence making betters gels. ILs can produce interesting soft matter systems, both potential-wise and scientifically.

We have performed a systematic and comprehensive study to establish the gelation kinetics of ionogels of laponite platelets in ionic liquid (IL), 1-ethyl-3-methyl imidazolium chloride, solutions at room temperature. The phenomenon of self-assembly of IL coated laponite platelets preceded gelation transition. In our earlier work, we discussed the two categories of ionogels produced one of which is a homogeneous and structured gel having high gel strength and the other one is a heterogeneous, fragile gel with low gel strength [39]. The binding was strongly dominated by electrostatic forces in low IL concentration samples whereas at higher IL concentration the network was held together by weak edge-face associations. Incidentally, the relaxations of density fluctuations were found to be governed by a fast and a slow mode. The fast mode contained two distinguishable components, one manifesting at low length scale and another operating at high length scale. Both these modes were diffusive and were IL concentration dependent. The slow mode, on the other hand, was observed to be frozen in space.

Ionic liquids are surfactant-like molecules with considerable surface activity. The complexity arises from the fact that the IL molecules interact with water molecules and laponite platelets simultaneously through electrostatic, hydrophobic and hydrogen bonding forces. In aqueous laponite dispersion (2% w/v) in presence of 1-methyl-3-ethylimidazolium chloride ionic liquid (IL, [C2mim] [Cl], concentration 0.01-0.05% (w/v). With aging, the time-dependent relative viscosity increased and the the time required for the system to get arrested decreases was increased from the IL concentration 0 to 0.03% (w/v). Hence, the arrest kinetics slows down as we increase IL concentration [39]. This time dependent behaviour was measured from dynamic light scattering studies revealing formation of IL mediated finite size colloidal networks on a time scale ≈ 4x103 s whereas the dispersion developed a large viscosity a decade in time later (≈ 4x104 s). Dynamic light scattering exhibited bimodal relaxation time of concentration fluctuations.

The behavior of laponite dispersions in ionic liquid (IL), 1-ethyl-3- methyl imidazolium, was studied by dynamic light scattering (DLS) in this manuscript. The results of this study suggest that the interaction between laponite dispersions may increase in a time-dependent manner. Hence, we conclude that the presence of ionic liquid greatly promotes the formation of gel network in aqueous laponite dispersions.

NJ acknowledges University Grants Commission, Government of India for a research fellowship. KR is thankful to Department of Science and Technology, Government of India-Inspire Faculty Award. This work was supported by a research grant received from Department of Science and Technology, Government of India.