Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2015) Volume 4, Issue 3
Prediction of Exchange rates has been a challenging task for traders and practitioners in modern financial markets. Statistical and econometric models are extensively used in the analysis and prediction of foreign exchange rates. This paper investigates the behavior of daily exchange rates of the Indian Rupee (INR) against the United States Dollar (USD), British Pound (GBP), Euro (EUR) and Japanese Yen (JPY). This paper attempts to examine the performance of ARIMA, Neural Network and Fuzzy neuron models in forecasting the currencies traded in Indian foreign exchange markets. Daily RBI reference exchange rates from January 2010-April 2015 were used for the analysis.
<Keywords: ARIMA, Forecasting, Fuzzy systems, Neural network
The foreign Exchange market in India started in 1978 when the government allowed banks to trade foreign exchange with one another. The globalization and liberalization have improved the scope for exchange market in India. The growth of foreign exchange market in the last decade has been phenomenal. Introduction of currency derivatives in Indian stock exchanges has increased the traded volume in exchange market by manifold. Corporates with exposure to the currency fluctuations in the market started trading in derivative markets.
In the last 5 years, from 2009 to 2014, trading volume in the foreign exchange market (including swaps, forwards and forward cancellations) has grown more than 25%1 . Figure 1 shows the growth of foreign exchange trading in India between 2009 and 2014. The interbank forex trading volume has accounted for 77% of the total trade during this period (2009-2014). This signifies that forex-market in India is dominated by inter-bank traders. Consequently, Indian forex market has emerged as one of the significant markets for global traders to make arbitrage gains. Several structural changes in the market led to efficient market place and reduced the scope for making abnormal profits. Hence, practitioners and traders use various sophisticated methods to predict forex markets. This paper analyses the behavior of Indian forex market using ARIMA, Neural Network and Fuzzy models and compare the performance of the models in the given scenario.
Several researchers have applied different techniques to understand forex rates. Patnaik examined Indian foreign exchange market and equilibrium exchange rate, using simulation techniques [1]. They found that there is a significant increase in the integration of domestic markets with international money markets. This is revealed by the increasing importance of interest differentials in the determination of the exchange rate. Kamruzzaman investigated three neural based forecasting models to predict six currencies namely USD, GBP, SGD, NZD, CHF and JPY against Australian dollar (AUD) using historical data and moving average technical indicators, and a comparison was made with the traditional ARIMA model [2]. They demonstrated that neural based model can forecast the forex rates more closely to the actuals. Zhang examined performance of Autoregressive Integrated Moving Average (ARIMA) model with simple regression model [3]. Rout developed an efficient exchange rate prediction scheme using an Autoregressive Moving Average (ARMA) structure with Differential Evolution (DE) Technique [4]. The prediction performance of rupees, yen and pound exchange rates with respect to US dollar was evaluated through the new model. In predicting the sunspot Chattopadhyay have applied ARIMA and Neural Network models. The results indicate that the performance of the autoregressive neural network-based model is much better than the autoregressive moving average and autoregressive integrated moving average-based models for the univariate forecast of the yearly mean sunspot numbers [5]. Durat compared three time series forecasting techniques using a classical statistical forecasting method and Artificial Neural Networks and Neo Fuzzy Neurons as emergent intelligent methods in predictingbirth rate in Spain [6]. They concluded that neo fuzzy neuron method better predicts the birth rate in Spain. Alam has examined the application of autoregressive model for forecasting and trading the BDT/USD exchange rates [7] from July 03, 2006 to April 30, 2010 as in-sample and May 01, 2010 to July 04, 2011 as out of sample data set. He concluded that the ARMA and AR models jointly outperform other models for forecasting the BDT2/USD exchange rate respectively in the context of statistical performance measures. Ayodele used ARIMA and Neural Networks models for Stock Price Prediction. Their results reveal the superiority of neural networks model over ARIMA model [8].
In the Indian context only a few studies were carried to predict exchange rates and stock market. However, those studies had applied individual models to study the behavior of the exchange rates. None of the studies compared the performance of different exchange rate prediction models. Perwej examined the effects of the number of inputs and hidden nodes and the size of the training sample on the insample and out-of-sample performance of Neural Networks [9]. They found that the number of input nodes have greater significance while deciding the neural network structure.
There is a lot of literature available on applications of fuzzy logic in financial predictive modeling. Tektaş has studied the performance of fuzzy model and ARIMA model to forecast weather in Istanbul and found that Fuzzy model yields better results [10]. Khashei found that fuzzy model effectively improved the forecasting accuracy than ARIMA and Neural network in predicting exchange rates in Iran [11]. Kumar studies shown that fuzzy logic predicts better than neural network in predicting prices in Indian stock markets [12]. Comparison of the performance of ARIMA, Neural Network and Fuzzy models in predicting prices in Indian stock market and exchange rate markets is untouched. Hence, this paper attempts to fill this research gap.
ARIMA (p, d, q) model
This paper used the exchange rate that covered the period from January 01, 2010, to April 30, 2015, having a total number of 1284 observations. It was observed that the original pattern of the time series of the index is not stationary. The time series have random walk pattern and vary randomly with no global trend or seasonality pattern observed. ADF test is used to determine whether a particular series is stationary or non-stationary. The ADF test values are reported in Table 1.
| Currency | Zero Level | P Value | 1st Level | P Value |
|---|---|---|---|---|
| USD | -0.51028 | 0.88670 | -27.4112 | 0.0000 |
| GBP | -0.65979 | 0.85450 | -34.1506 | 0.0000 |
| EURO | -1.06068 | 0.73300 | -33.2777 | 0.0000 |
| YEN | -1.7474 | 0.40710 | -35.8402 | 0.0000 |
Source: Authors Computations
Table 1: Test of Stationarity (ADF Test).
At the zero level all the exchange rate time series were nonstationary. Hence, lag differencing technique is used to convert these non-stationary series to stationary series. The reported ADF test values confirm the stationary of the series at 1st level i.e., the series are stationary series at first difference. Therefore, integrated term (p) is 1 in the ARIMA (p) structure for this study [13].
In order to construct the best ARIMA model for exchange rate time series, the autoregressive (p) and moving average (q) parameters are need to be identified for an effective model. After a time series has been stationarised by lag differencing, the next step in fitting an ARIMA model is to determine whether AR or MA terms are needed to correct any autocorrelation that remains in the differenced series. Autocorrelation (ACF) and partial-autocorrelation (PACF) correlograms were used to identify autoregressive term and moving average term. Since the ACF and PACF coefficients are not significant, we decided to determine the best model based on Bayesian Information Criterion (BIC) for various orders of autoregressive (p) and moving average (q) terms keeping integrated term (d) as order 1 [14]. Table 2 reports the values of BIC for various orders of ARIMA model for Indian Rupees against USD, GBP, Euro and Yen.
| ARIMA (p, d, q) | USD | GBP | Euro | Yen |
|---|---|---|---|---|
| (1,1,0) | 0.554702 | 1.594022 | 1.328843 | 1.484726 |
| (0,1,1) | 5.350015 | 6.439164 | 5.773487 | 5.147386 |
| (1,1,1) | 0.549155 | 1.592298 | 1.329075 | 1.479155 |
| (2,1,0) | 1.246268 | 2.32676 | 2.087253 | 2.169167 |
| (0,1,2) | 5.373939 | 6.457489 | 5.790546 | 5.172656 |
| (2,1,2) | 1.246485 | 2.336581 | 2.092735 | 2.173603 |
Source: Authors Computations
Table 2: BIC value for various orders of ARIMA.
Table 2 shows the different parameters p and q in the ARIMA model. Lowest BIC value is considered as best fit of the model. Hence, ARIMA (1, 1, 1) is considered the best for modelling USD, GBP and Yen and ARIMA (1, 1, 0) is considered the best for modelling Euro. In forecasting form, the general ARIMA model selected can be expressed as follows.
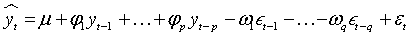 (1)
(1)
Where 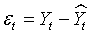 is the difference between the actual value and the forecast value of the series.
is the difference between the actual value and the forecast value of the series.
Neural network model
Forecasting of exchange rate poses many challenges. Exchange rates are influenced by many economic factors. As like economic time series exchange rate has trend cycle and irregularity. Classical time series analysis does not perform well on economics time series [15]. Hence, the idea of applying Neural Networks (NN) to forecast exchange rate is considered. NN tries to emulate human learning capabilities, creating models that represent the neurons in the human brain. Neurons are nervous cells that are the principal elements of the nervous central system. They can receive signals, process them and transmit electrical pulses to other neurons [16]. NN is composed of nodes or units connected by directed links. Each link has a numeric weight (ω is the weight matrix).
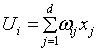
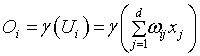
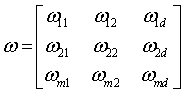
Where γ is the activation function, xj is the input neuron j, Oi is the output of the hidden neuron i, and W is theweight matrix. The NN learns by adjusting the weightmatrix. Therefore the general process responsible for training the network is mainly composed of three steps:
1. Feed forward the input signals
2. Back propagate the error
3. Adjust the weights
This paper applies nonlinear autoregressive neural network (NAR) model for predicting the exchange rates [17]. The structure of a NAN used in the present study is depicted in the below chart, 70% of the data contains training set and 30% of the data used for checking and validation (Figure 2).
Fuzzy model
In this paper, Adaptive Neuro-Fuzzy Inference System (ANFIS) is used for creating the fuzzy structure. ANFIS is a hybrid model which was first developed by Jang. ANFIS combines the learning skill by artificial neural networks with conjecture skill of expert opinion based FIS models [18]. It adjusts the membership functions of input and output variables and generates the rules related to input and output, automatically. ANFIS can produce all the rules by using the data set thus enabling the researchers to interpret these rules. Therefore, it is the widely used model in the studies of classification and estimation.
In an ANFIS model consisting of three inputs and one output,a typical rule set with base fuzzy if–then rules can be expressed as:
If X is Ai and Y is Bi and Z is Ci then
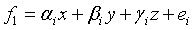 (2)
(2)
where α, β, and γ are linear output parameters. The ANFIS’ architecture with two inputs and one output is as shown.
ANFIS architecture to implement the three rules is shown in Figure 3.
Layer 1: In the first layer, each node generates membership grades to which they belong to each of the appropriate fuzzy sets such as high, medium and low sets using membership functions. This layer’s outputs are the fuzzy membership grade of the inputs. The linguistic variables of the fuzzy rules are expressed in the form of fuzzy sets and these variables are defined in terms of degree of membership functions with which the variables are associated. This method of calculating the degree of belongingness of the crisp input in the fuzzy set is called fuzzification, which is given by
O1,i= μAi(X) for i = 1,2,3 O1,i = μBi-3(Y) for i = 4,5,6 O1,i = μBi- 6(Z) for i = 7,8,9
Where, X, Y and Z are the crisp inputs to ith node, Ai, Bi, Ci (small, medium, large) are the linguistic labels characterized by appropriate membership functions μAi, μBi and μCi respectively. μ is membership function of the ANFIS. Triangular, Trapezoidal, Gaussian or Bell shape are the different methods of membership functions in ANFIS. Information is lost in the regions of membership functions where the slope is zero, as at these points the membership functions are not differentiable in triangular or trapezoidal membership functions. Therefore fuzzy systems with triangular or trapezoidal membership function can encounter problems of learning from data [18]. The gausssian membership function is also smoother than the bell shaped membership function [19]. Hence, Gaussian membership function is used in this study. The Gaussian membership function is as follows.
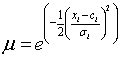 (3)
(3)
where Xi is the ith input variable, Ci is the ith center of the membership function for each fuzzy set, where the membership function achieves a maximum value, and σi is a constant related to the spread of the ith membership function.
Layer 2: In the second layer, every node multiplies product of the incoming signals and sends the product out. Each node output is the firing strength of a fuzzy rule. Oi,2 is the output 2 of the second layer.
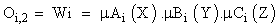 (4)
(4)
Layer 3: The third layer calculates the ratio of each ith fuzzy rule’s firing strength to the sum of all fuzzy rules’ firing strength. Consequently, Wi is taken as the normalized firing strength.
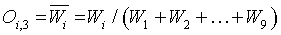 (5)
(5)
Layer 4: The nodes are adaptive in fourth layer. The output of each node in this layer is simply the product of a first order polynomial Sugeno model and the normalized firing strength. Thus, the outputs of this layer are given by
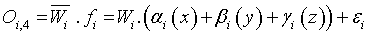 (6)
(6)
where Wi is the ith node’s output from the previous layer. Parameters αi, βi and γi are the coefficients of this linear combination and are also the parameter set in the consequent part of the Sugeno fuzzy model.
Layer 5: In the fifth layer is one single fixed node. This node computes the overall output by adding all the incoming signals as represented by the formula shown below.
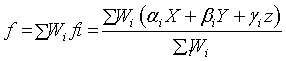 (7)
(7)
In this layer, the de-fuzzification process transforms each rule’s fuzzy results into a crisp output represented by f.
In this study, ANFIS was trained by hybrid learning algorithm. Out of 1284 days data, 896 days exchange rates were used as training data. Remaining 388 days data were used as checking data to formulate the ANFIS structure with 40 epochs (Figure 4).
Comparison of models
The above chart 4 plots the predicted exchange rates using ARIMA, NN and Fuzzy models with the actual exchange rates for the period from April 2014 to April 2015. The graphs clearly depict that fuzzy models deviates much from the actual for all the four currencies. Further to understand between NN and ARIMA, BIC and AIC values are computed. In order to fit the best model that shows the characteristics of actual return series, we applied Akaike’s Information criterion and Schwarz’s Bayesian Information criterion for model selection [20]. These two models apply the concept of information theory to measure amount of disorderliness in system. AIC and BIC were calculated using the formulae shown below.
Log Likelihood =(-T)/2(1+ln(2π)+ln(ěě/T)
Akaike info criterion (AIC) = -2(Log Likelihood/T) + 2(k/T)
Schwarz Bayes info criterion (BIC) = -2(Log Likelihood/T) + k ln((T)/T)
As per the AIC and BIC model selection, ARIMA has the lowest value among other models (Table 3). Hence, ARIMA best predicts the Indian exchange rates [21].
| ARIMA | NN | Fuzzy | ||
|---|---|---|---|---|
| USD | AIC | -3.38905 | -3.38193 | -3.37801 |
| BIC | -3.3836 | -3.37648 | -3.37256 | |
| GBP | AIC | -6.4023 | -6.38637 | -6.18149 |
| BIC | -6.39685 | -6.38092 | -6.17604 | |
| EURO | AIC | -7.34613 | -7.34627 | -7.32883 |
| BIC | -7.34068 | -7.34082 | -7.32338 | |
| YEN | AIC | -6.39327 | -6.38435 | -6.4469 |
| BIC | -6.38382 | -6.3789 | -6.44145 |
Source: Authors Computations
Table 3: Model selection.
This paper has examined predictability of exchange rates of Rupee against USD, GBP, Euro and Yen using classical time series method (ARIMA) and complex nonlinear methods such as Neural Network and Fuzzy neurons. Interestingly, the results and findings of the paper contradict with existing literature. Earlier studies confirm that neural network models performs better than ARIMA model [5,8] and fuzzy neuron model performs better than neural network model [6-12]. However, in predicting exchange rate market in India ARIMA model does better than those of the complex nonlinear models.