Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Review Article - (2014) Volume 1, Issue 2
In the present methodical study, FT-IR, FT-Raman and NMR spectra of the Propylbenzene were recorded and the fundamental vibrational frequencies were tabulated and assigned. The Gaussian hybrid computational calculations were carried out by HF and DFT (B3LYP and B3PW91) methods with 6-311+G(d,p) and 6-311++G(d,p) basis sets and the corresponding results were compared with experimental values. The change of chemical environment of present compound due to the addition of Ethyl and methyl chain was studied. Moreover, 13C NMR and 1H NMR were calculated by using the gauge independent atomic orbital (GIAO) method with B3LYP methods and the 6-311++G(d,p) basis set and their spectra were simulated and the chemical shifts related to TMS were compared. A study on the electronic and optical properties; absorption wavelengths, excitation energy, dipole moment and frontier molecular orbital energies, were performed by HF and DFT methods. The calculated HOMO and LUMO energies (kubo gap) were displayed in the figures which show that the occurring of charge transformation within the molecule. Besides frontier molecular orbitals (FMO), molecular electrostatic potential (MEP) was performed. NLO properties related to Polarizability and hyperpolarizability was also discussed. The local reactivity of the molecule has been studied using Fukui function.
<Keywords: Propylbenzene, Gauge independent atomic orbital, Chemical shifts, FMO, Fukui function
Propylbenzene is an organic compound that is based on the aromatic hydrocarbon with an aliphatic substitution. It is inflammable and colorless liquid, insoluble in water and less dense than water. The chemical is also flammable and incompatible with strong oxidizing agents. It is stable, but may form peroxides in storage if in contact with the air. It is important to test for the presence of peroxides before heating or distilling. Other synonyms of Propylbenzene are: n-Propylbenzene; Isocumene; Propylbenzene; 1-Phenylpropane; 1-Propylbenzene; Phenyl propane; Benzene, n-propyl. When there is contact between aromatic hydrocarbons and strong oxidizing agents it amounts to vigorous reactions sometimes amounting to explosions. They can react exothermically with bases and with diazo compounds. Substitution at the benzene nucleus occurs by halogenations (acid catalyst), nitration, sulfonation, and the Friedel-Crafts reaction.The propylbenzene is a byproduct while alkylation of benzene with propylene and it is useful a starting material for chemical synthesis [1]. Moreover, DIPB can be dehydrogenated to di-isopropenylbenzenes which can further be applied to produce plastics, elastomers and resins with valuable properties [2].
The literature survey reveals that, to the best of our knowledge, no intensive observation of spectroscopic [FT-IR and FT-Raman] and theoretical [HF/DFT] investigation has been reported so far. Therefore, the present investigation was undertaken to study the vibrational spectra, geometrical frame work review, inter and intra molecular interaction between HOMO and LUMO energy levels and first order hyperpolarizability of non linear optical (NLO) activity of the molecule.
The compound Propylbenzene is purchased from Sigma–Aldrich Chemicals, USA, which is of spectroscopic grade and hence used for recording the spectra as such without any further purification. The FT-IR spectrum of the compound is recorded in Bruker IFS 66V spectrometer in the range of 4000–400 cm−1. The spectral resolution is ±2 cm−1. The FT-Raman spectrum of same compound is also recorded in the same instrument with FRA 106 Raman module equipped with Nd:YAG laser source operating at 1.064 μm line widths with 200 μW power. The spectra are recorded in the range of 4000–100 cm−1 with scanning speed of 30 cm−1min−1 of spectral width 2 cm−1. The frequencies of all sharp bands are accurate to ±1 cm−1.
In the present work, HF and some of the hybrid methods; B3LYP and B3PW91 are carried out using the basis sets 6-31+G(d,p) and 6-311+G(d,p). All these calculations are performed using GAUSSIAN 09W [3] program package on Pentium IV processor in personal computer. In DFT methods; Becke’s three parameter hybrids function combined with the Lee-Yang-Parrcorrelation function (B3LYP) [4,5], Becke’s three parameter exact exchange-function (B3) [6] combined with gradient-corrected correlational functional of Lee, Yang and Parr (LYP) [7,8] and Perdew and Wang (PW91) [9,10] predict the best results for molecular geometry and vibrational frequencies for moderately larger molecules. The calculated frequencies are scaled down to give up the rational with the observed frequencies. The scaling factors are 0.959, 1.028, 1.297 for HF/6-311++G(d,p). For B3LYP/6-311+/6- 311++G(d,p) basis set, the scaling factors are 0.993, 0.810/0.994,1.046, 1.09. For B3PW91/6-31+G/6-311+G(d,p) basis set, the scaling factors are 0.983, 1.04,1.08/1.01, 0.940,0.794. The optimized molecular structure of the molecule is obtained from Gaussian 09 and Gaussview program and is shown in Figure 1. The comparative optimized structural parameters such as bond length, bond angle and dihedral angle are presented in Table 1. The observed (FT-IR and FT-Raman) and calculated vibrational frequencies and vibrational assignments are submitted in Table 2. Experimental and simulated spectra of IR and Raman are presented in the Figures 2 and 3.
| Geometrical parameter | HF/ 6-311+G(d,p) | HF/ 6-311++G (d,p) | B3LYP/ 6-311 +G (d,p) | B3LYP/ 6-311++G(d, p) | B3PW91/ 6-311+G(d,p) | B3PW91/ 6-311++G(d,p) |
|---|---|---|---|---|---|---|
| Bond length(Å) | ||||||
| C1-C2 | 1.390 | 1.390 | 1.399 | 1.399 | 1.393 | 1.397 |
| C1-C6 | 1.385 | 1.386 | 1.393 | 1.393 | 1.388 | 1.391 |
| C1-H7 | 1.076 | 1.007 | 1.085 | 1.085 | 1.085 | 1.086 |
| C2-C3 | 1.390 | 1.390 | 1.399 | 1.399 | 1.393 | 1.397 |
| C2-C12 | 1.513 | 1.513 | 1.512 | 1.512 | 1.507 | 1.507 |
| C3-C4 | 1.385 | 1.385 | 1.393 | 1.393 | 1.388 | 1.391 |
| C3-H8 | 1.076 | 1.076 | 1.085 | 1.085 | 1.085 | 1.086 |
| C4-C5 | 1.385 | 1.385 | 1.393 | 1.394 | 1.388 | 1.391 |
| C4-H9 | 1.075 | 1.075 | 1.084 | 1.084 | 1.083 | 1.085 |
| C5-C6 | 1.385 | 1.585 | 1.394 | 1.394 | 1.388 | 1.391 |
| C5-H10 | 1.075 | 1.075 | 1.084 | 1.084 | 1.083 | 1.085 |
| C6-H11 | 1.075 | 1.075 | 1.084 | 1.084 | 1.083 | 1.085 |
| C12-C13 | 1.535 | 1.535 | 1.541 | 1.541 | 1.533 | 1.535 |
| C12-H17 | 1.087 | 1.087 | 1.095 | 1.095 | 1.094 | 1.096 |
| C12-H18 | 1.087 | 1.087 | 1.095 | 1.095 | 1.094 | 1.096 |
| C13-H14 | 1.087 | 1.087 | 1.095 | 1.095 | 1.094 | 1.096 |
| C13-C15 | 1.527 | 1.527 | 1.530 | 1.530 | 1.524 | 1.525 |
| C13-H16 | 1.087 | 1.087 | 1.095 | 1.095 | 1.094 | 1.096 |
| C15-H19 | 1.086 | 1.086 | 1.093 | 1.093 | 1.092 | 1.093 |
| C15-H20 | 1.087 | 1.087 | 1.094 | 1.094 | 1.093 | 1.095 |
| C15-H21 | 1.087 | 1.087 | 1.094 | 1.094 | 1.093 | 1.095 |
| Bond Angle(º) | ||||||
| C2-C1-C6 | 121.024 | 121.024 | 121.059 | 121.057 | 121.010 | 121.049 |
| C2-C1-H7 | 119.540 | 119.540 | 119.350 | 119.383 | 119.350 | 119.352 |
| C6-C1-H7 | 119.434 | 119.434 | 119.638 | 119.558 | 119.638 | 119.598 |
| C1-C2-C3 | 118.182 | 118.181 | 118.247 | 118.145 | 118.247 | 118.158 |
| C1-C2-C12 | 120.903 | 120.902 | 120.861 | 120.909 | 120.861 | 120.908 |
| C3-C2-C12 | 120.903 | 120.904 | 120.865 | 120.922 | 120.865 | 120.906 |
| C2-C3-C4 | 121.024 | 121.025 | 121.010 | 121.056 | 121.010 | 121.049 |
| C2-C3-H8 | 119.540 | 119.539 | 119.351 | 119.386 | 119.351 | 119.352 |
| C4-C3-H8 | 119.435 | 119.434 | 119.638 | 119.556 | 119.638 | 119.598 |
| C3-C4-C5 | 120.201 | 120.200 | 120.131 | 120.144 | 120.131 | 120.143 |
| C3-C4-H9 | 119.750 | 119.751 | 119.814 | 119.799 | 119.814 | 119.799 |
| C5-C4-H9 | 120.047 | 120.048 | 120.053 | 120.055 | 120.053 | 120.055 |
| C4-C5-C6 | 119.366 | 119.367 | 119.469 | 119.452 | 119.469 | 119.455 |
| C4-C5-H10 | 120.316 | 120.316 | 120.265 | 120.273 | 120.265 | 120.271 |
| C6-C5-C10 | 120.316 | 120.315 | 120.265 | 120.273 | 120.265 | 120.271 |
| C1-C6-C5 | 120.201 | 120.200 | 120.131 | 120.143 | 120.131 | 120.143 |
| C1-C6-H11 | 119.751 | 119.751 | 119.814 | 119.800 | 119.814 | 119.799 |
| C5-C6-H11 | 120.047 | 120.047 | 120.053 | 120.055 | 120.053 | 120.056 |
| C2-C12-C13 | 113.214 | 113.218 | 112.942 | 113.225 | 112.942 | 112.984 |
| C2-C12-H17 | 109.311 | 109.310 | 109.552 | 109.515 | 109.552 | 109.546 |
| C2-C12-H18 | 109.312 | 109.314 | 109.550 | 109.518 | 109.550 | 109.551 |
| C13-C12-H17 | 109.148 | 109.144 | 109.045 | 108.940 | 109.045 | 109.060 |
| C13-C12-H18 | 109.149 | 109.145 | 109.046 | 108.941 | 109.046 | 109.057 |
| H17-C12-H18 | 106.483 | 106.486 | 106.495 | 106.474 | 106.495 | 106.426 |
| C12-C13-H14 | 109.131 | 109.131 | 108.989 | 108.972 | 108.989 | 108.944 |
| C12-C13-C15 | 112.702 | 112.701 | 112.693 | 112.872 | 112.693 | 112.893 |
| C12-C13-H16 | 109.133 | 109.132 | 108.990 | 108.972 | 108.990 | 108.941 |
| H14-C13-C15 | 109.686 | 109.689 | 109.921 | 109.842 | 109.9213 | 109.926 |
| H14-C13-H16 | 106.295 | 109.294 | 106.103 | 106.102 | 106.103 | 105.970 |
| C15-C13-H16 | 109.685 | 109.686 | 109.921 | 109.845 | 109.921 | 109.922 |
| C13-C15-H19 | 111.070 | 111.065 | 111.376 | 111.269 | 111.376 | 111.322 |
| C13-C15-H20 | 111.212 | 111.213 | 111.180 | 111.258 | 111.180 | 111.297 |
| C13-C15-H21 | 111.211 | 111.211 | 111.181 | 111.261 | 111.181 | 111.295 |
| H19-C15-H20 | 107.732 | 107.741 | 107.685 | 107.655 | 107.685 | 107.614 |
| H19-C15-H21 | 107.732 | 107.741 | 107.684 | 107.655 | 107.684 | 107.613 |
| H20-C15-H21 | 107.699 | 107.699 | 107.548 | 107.552 | 107.548 | 107.501 |
| Dihedral Angle (º) | ||||||
| C6-C1-C2-C3 | -0.2286 | -0.2368 | -0.1521 | -0.1869 | -0.1521 | -0.1666 |
| C6 -C1-C2-C12 | 178.5556 | 178.5336 | 178.0406 | 178.1085 | 178.0406 | 177.9944 |
| H7-C1-C2-C3 | 179.5007 | 179.5038 | 179.5501 | 179.5035 | 179.5501 | 179.5225 |
| H7-C1-C2-C12 | -1.7151 | -1.7257 | -2.2572 | -2.2012 | -2.2572 | -2.3165 |
| C2-C1-C6-C5 | 0.0739 | 0.0838 | 0.0302 | 0.0399 | 0.0302 | 0.0255 |
| C2-C1-C6-H11 | 179.829 | 179.8267 | 179.776 | 179.7575 | 179.776 | 179.747 |
| H7-C1-C6-C5 | -179.6557 | -179.6572 | -179.6712 | -179.6499 | -179.6712 | -179.6628 |
| H7-C1-C6-H11 | 0.0994 | 0.0858 | 0.0746 | 0.0677 | 0.0746 | 0.0587 |
| C1-C2-C3-C4 | 0.2286 | 0.2368 | 0.1525 | 0.1871 | 0.1525 | 0.1667 |
| C1-C2-C3-H8 | -179.4989 | -179.5024 | -179.5501 | -179.5054 | -179.5501 | -179.5221 |
| C12-C2-C3-C4 | -178.5556 | -178.5336 | -178.0401 | -178.1081 | -178.0401 | -177.9944 |
| C12-C2-C3-H8 | 1.7169 | 1.7272 | 2.2573 | 2.1995 | 2.2573 | 2.3169 |
| C1-C2-C12-C13 | -89.3641 | -89.3567 | -89.0743 | -89.0714 | -89.0743 | -89.0769 |
| C1-C2-C12-H17 | 32.5395 | 32.5431 | 32.6862 | 32.7195 | 32.6862 | 32.7267 |
| C1-C2-C12-H18 | 148.7309 | 148.7389 | 149.165 | 149.1335 | 149.165 | 149.1201 |
| C3-C2-C12-C13 | 89.3802 | 89.3802 | 89.071 | 89.1765 | 89.071 | 89.0334 |
| C3-C2-C12-H17 | -148.7094 | -148.7201 | -149.1686 | -149.0326 | -149.1686 | -149.1631 |
| C3-C2-C12-H18 | -32.518 | -32.5243 | -32.6898 | -32.6186 | -32.6898 | -32.7696 |
| C2-C3-C4-C5 | -0.074 | -0.0838 | -0.031 | -0.0404 | -0.031 | -0.0257 |
| C2-C3-C4-H9 | -179.8288 | -179.8268 | -179.7766 | -179.759 | -179.7766 | -179.7468 |
| H8-C3-C4-H9 | 179.6539 | 179.6557 | 179.6707 | 179.6516 | 179.6707 | 179.6622 |
| H8-C3-C4-H9 | -0.1009 | -0.0873 | -0.0749 | -0.0671 | -0.0749 | -0.0589 |
| C3-C4-C5-C6 | -0.0862 | -0.0751 | -0.0942 | -0.1109 | -0.0942 | -0.1189 |
| C3-C4-C5-H10 | -179.8106 | -179.8093 | -179.8245 | -179.8336 | -179.8245 | -179.8281 |
Table 1: The optimized geometrical parameters of propylbenzene.
| S. No | Symmetry Species C s | Observed Frequency(cm-1) | Methods | Vibrational Assignments | |||||
|---|---|---|---|---|---|---|---|---|---|
| FT-IR | FT-Raman | HF | B3LYP | B3PW91 | |||||
| 6-311+G (d, p) | 6-311+G (d, p) | 6-311++G (d, p) | 6-311+G (d, p) | 6-311++G (d, p) | |||||
| 1 | A′ | 3090w | - | 3093 | 3097 | 3095 | 3090 | 3096 | (C-H) υ |
| 2 | A′ | 3080m | - | 3080 | 3084 | 3082 | 3079 | 3083 | (C-H) υ |
| 3 | A′ | - | 3070m | 3071 | 3076 | 3073 | 3070 | 3075 | (C-H) υ |
| 4 | A′ | - | 3060m | 3059 | 3063 | 3060 | 3057 | 3062 | (C-H) υ |
| 5 | A′ | - | 3040s | 3056 | 3062 | 3059 | 3056 | 3060 | (C-H) υ |
| 6 | A′ | 3030s | - | 2976 | 2997 | 2994 | 2998 | 3006 | (C-H) υ |
| 7 | A′ | - | 3010w | 2973 | 2994 | 2991 | 2993 | 3001 | (C-H) υ |
| 8 | A′ | 3005w | 3005w | 2956 | 2972 | 2970 | 2973 | 2979 | (C-H) υ |
| 9 | A′ | 2960s | 2937 | 2951 | 2949 | 2954 | 2958 | (C-H) υ | |
| 10 | A′ | 2940s | 2927 | 2937 | 2935 | 2935 | 2938 | (C-H) υ | |
| 11 | A′ | 2930s | - | 2920 | 2931 | 2930 | 2930 | 2931 | (C-H) υ |
| 12 | A′ | - | 2870m | 2912 | 2928 | 2925 | 2927 | 2929 | (C-H) υ |
| 13 | A′ | 1610w | - | 1653 | 1596 | 1596 | 1621 | 1605 | (C=C) υ |
| 14 | A′ | 1605w | 1605m | 1628 | 1578 | 1575 | 1599 | 1584 | (C=C) υ |
| 15 | A′ | 1590w | 1590m | 1524 | 1513 | 1558 | 1490 | 1478 | (C=C) υ |
| 16 | A″ | 1500s | - | 1505 | 1499 | 1503 | 1461 | 1454 | (CH3) α |
| 17 | A′ | 1495s | - | 1491 | 1486 | 1490 | 1448 | 1443 | (C-C) υ |
| 18 | A′ | 1455m | - | 1442 | 1484 | 1442 | 1440 | 1436 | (C-C) υ |
| 19 | A′ | 1450s | - | 1436 | 1476 | 1434 | 1438 | 1430 | (C-C) υ |
| 20 | A′ | - | 1440w | 1428 | 1421 | 1429 | 1433 | 1428 | (C-C) υ |
| 21 | A′ | 1380w | - | 1374 | 1353 | 1361 | 1363 | 1354 | (C-C) υ |
| 22 | A′ | 1340w | 1340w | 1352 | 1325 | 1333 | 1323 | 1330 | (C-C) υ |
| 23 | A′ | - | 1290w | 1315 | 1305 | 1312 | 1293 | 1316 | (C-H) δ |
| 24 | A′ | - | 1280w | 1277 | 1286 | 1294 | 1267 | 1306 | (C-H) δ |
| 25 | A′ | - | 1250w | 1272 | 1267 | 1275 | 1253 | 1273 | (C-H) δ |
| 26 | A′ | - | 1200s | 1221 | 1262 | 1203 | 1253 | 1262 | (C-H) δ |
| 27 | A′ | - | 1190w | 1181 | 1196 | 1193 | 1186 | 1201 | (C-H) δ |
| 28 | A′ | - | 1180w | 1170 | 1175 | 1172 | 1174 | 1188 | (C-H) δ |
| 29 | A′ | 1160w | 1160w | 1150 | 1152 | 1149 | 1142 | 1157 | (C-H) δ |
| 30 | A′ | 1105w | - | 1100 | 1132 | 1129 | 1117 | 1137 | (C-H) δ |
| 31 | A′ | 1100w | - | 1106 | 1094 | 1075 | 1100 | 1069 | (C-H) δ |
| 32 | A′ | 1095w | 1095w | 1077 | 1078 | 1059 | 1094 | 1057 | (C-H) δ |
| 33 | A′ | 1050w | - | 1051 | 1041 | 1023 | 1051 | 1019 | (C-H) δ |
| 34 | A′ | 1040w | - | 1032 | 1022 | 1004 | 1036 | 1007 | (C-H) δ |
| 35 | A′ | 1030w | - | 1024 | 1010 | 993 | 1032 | 1002 | (C-C) δ |
| 36 | A′ | - | 1000s | 1018 | 990 | 972 | 1001 | 968 | (C-C) δ |
| 37 | A′ | 910w | 943 | 974 | 952 | 997 | 913 | (C-C) δ | |
| 38 | A″ | 895w | - | 929 | 956 | 937 | 979 | 902 | (C-H) γ |
| 39 | A″ | 890w | 890w | 882 | 868 | 886 | 895 | 896 | (C-H) γ |
| 40 | A″ | - | 865w | 824 | 835 | 855 | 839 | 871 | (C-H) γ |
| 41 | A″ | - | 840w | 814 | 821 | 841 | 815 | 846 | (C-H) γ |
| 42 | A″ | 820w | 820 | 806 | 798 | 815 | 802 | 826 | (C-H) γ |
| 43 | A″ | 740vs | 740vs | 757 | 770 | 788 | 771 | 760 | (C-H) γ |
| 44 | A″ | 705vs | - | 710 | 711 | 727 | 714 | 700 | (C-H) γ |
| 45 | A″ | 700vs | - | 682 | 697 | 713 | 691 | 682 | (C-H) γ |
| 46 | A″ | - | 610m | 664 | 665 | 649 | 666 | 655 | (C-H) γ |
| 47 | A″ | 590s | 590w | 583 | 594 | 580 | 591 | 581 | (C-H) γ |
| 48 | A″ | 570vs | 550 | 559 | 546 | 558 | 547 | (C-H) γ | |
| 49 | A″ | 530vw | 505 | 493 | 542 | 496 | 489 | (C-H) γ | |
| 50 | A′ | 490s | - | 418 | 410 | 442 | 404 | 398 | (CCC) δ |
| 51 | A′ | 480s | - | 341 | 343 | 370 | 337 | 332 | (CCC) δ |
| 52 | A′ | 470vw | - | 305 | 307 | 330 | 302 | 299 | (CCC) δ |
| 53 | A″ | 400 m | - | 278 | 276 | 297 | 271 | 266 | (CCC) γ |
| 54 | A″ | 370m | 238 | 227 | 245 | 225 | 222 | (CCC) γ | |
| 55 | A″ | 280s | - | 103 | 101 | 109 | 99 | 98 | (CCC) γ |
| 56 | A″ | 270s | - | 84 | 82 | 89 | 82 | 80 | (C-C) γ |
| 57 | A″ | 260s | _- | 37 | 45 | 48 | 38 | 43 | (C-C) γ |
Table 2: Observed and calculated vibrational frequencies of propylbenzene using HF and DFT (B3LYP & B3PW91) at the 6-31+& 6-311+G (d, p) level.
The 1H and 13C NMR isotropic shielding are calculated with the GIAO method [11] using the optimized parameters obtained from B3LYP/6-311++G(d,p) method. 13C isotropic magnetic shielding (IMS) of any X carbon atoms is made according to value 13C IMS of TMS, CSX=IMSTMS-IMSx. The 1H and 13C isotropic chemical shifts of TMS at B3LYP methods with 6-311++G(d,p) level using the IEFPCM method in DMSO, Nitromethene and CCl4. The absolute chemical shift is found between isotropic peaks and the peaks of TMS [12]. The electronic properties; HOMO-LUMO energies, absorption wavelengths and oscillator strengths are calculated using B3LYP method of the time-dependent DFT (TD-DFT) [13,14] method in gas phase and solvent phase. Moreover, the dipole moment, nonlinear optical (NLO) properties, linear polarizabilities and first hyperpolarizabilities have also been studied. The local reactivity of the molecule has been studied using Fukui function. The condensed softness indices are found and it is used to predict both the reactive centers and possible sites of nucleophilic and electrophilic attacks.
Molecular geometry
The molecular structure of Propylbenzene belongs to CS point group symmetry. The optimized structure of the molecule is obtained from Gaussian 09 and Gauss view program [15] and is shown in Figure 1. The present molecule contains two ethyl and one methyl groups which are loaded in the left moiety. The hexagonal structure of the benzene is broken at the point of substitution due to the addition of heavy mass. It is also evident that, the bond length (C1-C2&C2-C3) at the point of substitution is 0.059Å is greater than rest of others in the ring. Consequently, the property of the same also changed with respect to the ligand (ethyl and methyl groups). The bond angle of C1-C2-C3 is 1.306º elevated than C4-C5-C6 in the ring which also conform the breaking of hexagonal shield.
The structure optimization and zero point vibrational energy of the compound in HF and DFT(B3LYP/B3PW91) with 6-311+/6-311+G(d,p) are 123.00, 115.69, 115.679, 116.943,and 115.89 Kcal/Mol, respectively.The calculated value of HF is greater than the values of DFT method because the assumption of ground state energy in HF is greater than the true energy. Though, both C loaded by CH2, the bond length values between C2-C12 and C12-C13 are differed 0.0290 Å since further weighted by CH3 in the chain. The entire C-H bonds in the chain and methyl group having almost equal inter nuclear distance. Form the optimized molecular structure; it is observed that there is no arithmetical change in the chain. So there is no further change in geometrical property.
Vibrational assignments
In order to obtain the spectroscopic signature of the propylbenzene, the computational calculations are performed for frequency analysis. The molecule, has CS point group symmetry, consists of 21 atoms, so it has 57 normal vibrational modes. On the basis of Cs symmetry, the 57 fundamental vibrations of the molecule can be distributed as 39 in-plane vibrations of A′ species and 18 out of plane vibrations of A″ species, i.e., Γvib = 39 A′ + 18 A″. In the CS group symmetry of molecule is non-planar structure and has the 57 vibrational modes span in the irreducible representations.
The harmonic vibrational frequencies (unscaled and scaled) calculated at HF, B3LYP and B3PW91 levels using the triple split valence basis set along with the diffuse and polarization functions, 6-31+/6-311++G(d,p) and observed FT-IR and FT-Raman frequencies for various modes of vibrations have been presented in Tables 2 and 3. Comparison of frequencies calculated at HF andB3LYP/B3PW91 with the experimental values reveal the over estimation of the calculated vibrational modes due to the neglect of a harmonicity in real system. Inclusion of electron correlation in the density functional theory to certain extends makes the frequency values smaller in comparison with the HF frequency data. Reduction in the computed harmonic vibrations, although basis set sensitive is only marginal as observed in the DFT values using 6-311+G (d,p).
| S. No. | Observed frequency | Calculated frequency | ||||
|---|---|---|---|---|---|---|
| HF | B3LYP | B3PW91 | ||||
| 6-311+G (d, p) | 6-31+G (d, p) | 6-311+G (d, p) | 6-31+G (d, p) | 6-311+G (d, p) | ||
| 1 | 3090w | 3347 | 3187 | 3187 | 3211 | 3198 |
| 2 | 3080m | 3333 | 3174 | 3174 | 3199 | 3185 |
| 3 | 3070m | 3323 | 3166 | 3165 | 3190 | 3176 |
| 4 | 3060m | 3310 | 3152 | 3152 | 3176 | 3163 |
| 5 | 3040s | 3307 | 3151 | 3151 | 3175 | 3161 |
| 6 | 3030s | 3220 | 3084 | 3084 | 3115 | 3105 |
| 7 | 3010w | 3217 | 3081 | 3081 | 3110 | 3100 |
| 8 | 3005w | 3199 | 3059 | 3058 | 3089 | 3077 |
| 9 | 2960s | 3178 | 3037 | 3037 | 3069 | 3055 |
| 10 | 2940s | 3167 | 3023 | 3023 | 3050 | 3035 |
| 11 | 2930s | 3160 | 3017 | 3017 | 3044 | 3028 |
| 12 | 2910m | 3151 | 3013 | 3012 | 3041 | 3025 |
| 13 | 1610w | 1789 | 1643 | 1643 | 1684 | 1658 |
| 14 | 1605w | 1762 | 1622 | 1622 | 1661 | 1636 |
| 15 | 1590w | 1649 | 1525 | 1525 | 1548 | 1527 |
| 16 | 1500s | 1629 | 1510 | 1510 | 1518 | 1502 |
| 17 | 1495s | 1614 | 1497 | 1497 | 1505 | 1491 |
| 18 | 1455m | 1614 | 1495 | 1495 | 1503 | 1488 |
| 19 | 1450s | 1607 | 1487 | 1487 | 1501 | 1482 |
| 20 | 1440w | 1598 | 1482 | 1482 | 1496 | 1479 |
| 21 | 1380w | 1537 | 1411 | 1411 | 1423 | 1403 |
| 22 | 1340w | 1513 | 1382 | 1382 | 1402 | 1378 |
| 23 | 1290w | 1471 | 1361 | 1361 | 1371 | 1363 |
| 24 | 1280w | 1429 | 1342 | 1342 | 1343 | 1353 |
| 25 | 1250w | 1423 | 1322 | 1322 | 1328 | 1319 |
| 26 | 1200s | 1366 | 1316 | 1316 | 1328 | 1308 |
| 27 | 1190w | 1321 | 1248 | 1248 | 1257 | 1244 |
| 28 | 1180w | 1309 | 1226 | 1226 | 1244 | 1231 |
| 29 | 1160w | 1287 | 1202 | 1202 | 1210 | 1199 |
| 30 | 1105w | 1231 | 1181 | 1181 | 1184 | 1178 |
| 31 | 1100w | 1199 | 1124 | 1124 | 1132 | 1122 |
| 32 | 1095w | 1168 | 1108 | 1108 | 1126 | 1110 |
| 33 | 1050w | 1139 | 1070 | 1070 | 1082 | 1070 |
| 34 | 1040w | 1119 | 1050 | 1050 | 1066 | 1057 |
| 35 | 1030w | 1110 | 1038 | 1038 | 1062 | 1052 |
| 36 | 1000s | 1104 | 1017 | 1017 | 1030 | 1016 |
| 37 | 910w | 1097 | 1001 | 996 | 1026 | 995 |
| 38 | 895w | 1081 | 982 | 980 | 1007 | 980 |
| 39 | 890w | 1026 | 929 | 927 | 949 | 926 |
| 40 | 865w | 959 | 894 | 894 | 912 | 900 |
| 41 | 840w | 947 | 879 | 879 | 886 | 874 |
| 42 | 820w | 938 | 854 | 853 | 872 | 853 |
| 43 | 740vs | 881 | 824 | 824 | 838 | 826 |
| 44 | 705vs | 826 | 761 | 760 | 776 | 761 |
| 45 | 700vs | 794 | 746 | 746 | 751 | 741 |
| 46 | 610m | 772 | 712 | 712 | 724 | 712 |
| 47 | 590s | 678 | 636 | 636 | 642 | 632 |
| 48 | 570vs | 640 | 598 | 599 | 606 | 595 |
| 49 | 530vw | 547 | 507 | 507 | 515 | 505 |
| 50 | 490s | 452 | 413 | 414 | 420 | 411 |
| 51 | 480s | 369 | 346 | 346 | 350 | 343 |
| 52 | 470vw | 330 | 309 | 309 | 314 | 309 |
| 53 | 400 m | 301 | 278 | 278 | 282 | 275 |
| 54 | 370m | 258 | 229 | 229 | 234 | 229 |
| 55 | 280s | 112 | 102 | 102 | 103 | 101 |
| 56 | 270s | 91 | 83 | 83 | 85 | 83 |
| 57 | 260s | 40 | 45 | 45 | 40 | 44 |
Table 3: Calculated unscaled frequencies of propyl benzene using HF/DFT (B3LYP&B3PW91) with 6-31+(d,p) and 6-311+G(d,p) basis sets.
C-H Vibrations: The C–H stretching vibrations are normally observed in the region 3100–3000 cm−1 for aromatic benzene structure [16,17] which shows their uniqueness of the skeletal vibrations. The bands appeared at 3090, 3070, 3065, 3060 and 3040 cm−1 in the Propylbenzene have been assigned to C–H ring stretching vibrations. The C–H in-plane ring bending vibrations are normally occurred as a number of strong to weak intensity bands in the region 1300-1000 cm−1 [18]. In the present case, four C–H in-plane bendingvibrations of the present compound are identified at 1290, 1280, 1250 and 1200 cm 1. The calculated frequencies for B3LYP/6-31++G (d,p) and B3LYP/6- 311++G (d, p) methods for C–H in-plane bending vibrations showed excellent agreement with recorded spectrum as well as literature data. The C–H out-of-plane bending vibrationsare normally observed in the region 1000–809 cm−1 [19]. The C–H out of plane bending vibrations is observed at 895, 890, 865, 840 and 820 cm−1. The entire C-H stretching and bending vibrations are located at the top end of the expected region which is because of these vibrations have not affected by ethyl and methyl group in the molecule. Whereas, all the out of plane bending vibrations are suppressed to the lower end of the expected region.
Methyl groups vibrations: With the aromatic ring, for the substitution of CH3 group, the vibrational frequencies for nine fundamental vibrations such as three stretching, in plane and out of plane bending vibrations normally observed in the region of 3000- 2750 cm-1, 1250-950 cm-1 and 950- 720 cm-1 [19,20], respectively.
Accordingly, the stretching vibrational peaks are observed at 3030, 3010 and 3005 cm-1, in plane bending vibrational bands are found at 1180, 1160, and1105 cm-1 and out of plane bending signals are identified at 740, 705 and 700 cm-1. All the CH3 stretching vibrations are located in asymmetric range which shows the enhancement of CH3 group vibrations in the present molecule. Except, two out of plane vibrations, the entire bending signals are received within the expected region. The ethyl group in the chain influences the bending vibrations of CH3. The above assignments go along with the literature of R.N. Singh and Varsanyi [19,20].
Ethyl group vibrations: The aliphatic chain substitution CH2 ethyl group with the aromatic ring will have eight fundamental vibrations such as four stretching, in plane and out of plane bending vibrations normally found in the region of 3000 -2850, 1300-1000 cm-1 and 810- 722 cm-1 [21,22], respectively. In the present study of propylbenzene the stretching vibrations are observed at 2960,2930, 2910, 2870 cm-1 , the in-plane bending vibrations are found at 1100, 1095, 1050, 1040 cm-1 and subsequently out of plane vibrations are at 610, 590, 570 and 530 cm-1. All the stretching and bending vibrational bands are found within the region.
C-C vibrations: The bands due the C-C stretching vibrations are called skeletal vibrations normally observed in the region 1430 - 1650 cm-1 for the aromatic ring compounds [23,24]. Socrates [25] mentioned that, the presence of conjugate substituent suchas C=C causesstretching peaks around the region 1625-1575 cm-1. As predicted in the earlier references, in this title compound,the prominent peaks are found with strong and medium intensity at 1610, 1605 and 1590 cm-1 due to C=C stretching vibrations. The C-C stretching vibrations are appeared at1495, 1455 and1450 cm-1. The CCCin-plane and out of plane bending vibrations are appeared at 490, 480 and 470 cm-1 and 400, 370 and 280 cm-1. Similar to the ring C-H vibrations, these skeletal CC stretching and bending vibrations are found within the expected region and also make a good agreement with literature [26].
NMR assessment: NMR spectroscopy is currently used for structure elucidation of complex molecules. The combined use of experimental and computationaltools offers a powerful gadget to interpret and predict the structure of bulky molecules. The optimized structure of Propylbenzene is used to calculate the NMR spectra at B3LYP method with 6-311++G(d,p) level using the GIAO method and the chemical shifts of the compound are reported in ppm relative to TMS for 1H and 13C NMR spectra which are presented in Table 4. The corresponding spectra are shown in Figure 4.
| Atom position | Gas | Solvent | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Chloroform | DMSO | ||||||||
| B3LYP/6-311+G(d,p) (ppm) | B3LYP/6-311+G (2d,p) GIAO (ppm) | Shift (ppm) | B3LYP/6-311+G(d,p) (ppm) | B3LYP/6-311+G(2d,p) GIAO (ppm) | Shift (ppm) | B3LYP/6-311+G(d,p) (ppm) | B3LYP/6-311+G(2d,p) GIAO (ppm) | Shift (ppm) | |
| C1 | 50.6257 | 131.84 | 81.2143 | 50.6257 | 131.84 | 81.2143 | 50.2521 | 132.214 | 81.9619 |
| C2 | 35.1536 | 147.312 | 112.1584 | 35.1536 | 147.312 | 112.1584 | 33.6205 | 148.845 | 115.2245 |
| C3 | 52.5577 | 129.908 | 77.3503 | 52.5577 | 129.908 | 77.3503 | 52.2505 | 130.215 | 77.9645 |
| C4 | 48.1658 | 134.3 | 86.1342 | 48.1658 | 134.3 | 86.1342 | 48.155 | 134.31 | 86.155 |
| C5 | 51.9287 | 130.537 | 78.6083 | 51.9287 | 130.53 | 78.6013 | 52.2318 | 130.234 | 78.0022 |
| C6 | 48.5706 | 133.89 | 85.3194 | 48.5706 | 133.89 | 85.3194 | 48.5497 | 133.916 | 85.3663 |
| C12 | 142.636 | 39.8297 | 102.8063 | 142.636 | 39.8297 | 102.8063 | 142.899 | 39.5661 | 103.3329 |
| C13 | 167.62 | 14.846 | 152.774 | 167.62 | 14.846 | 152.774 | 167.836 | 14.6298 | 153.2062 |
| C15 | 169.06 | 13.4059 | 155.6541 | 169.06 | 13.4059 | 155.6541 | 169.613 | 12.8531 | 156.7599 |
| 7H | 24.3718 | 7.5103 | 16.8615 | 24.3718 | 7.5103 | 16.8615 | 24.1899 | 7.6922 | 16.4977 |
| 8H | 24.1444 | 7.7377 | 16.4067 | 24.1444 | 7.7377 | 16.4067 | 23.9782 | 7.9039 | 16.0743 |
| 9H | 24.286 | 7.5961 | 16.6899 | 24.286 | 7.5961 | 16.6899 | 24.1354 | 7.7467 | 16.3887 |
| 10H | 24.4747 | 7.4074 | 17.0673 | 24.4747 | 7.4074 | 17.0673 | 24.3433 | 7.5388 | 16.8045 |
| 11H | 24.2974 | 7.5847 | 16.7127 | 24.2974 | 7.5847 | 16.7127 | 24.1446 | 7.7375 | 16.4071 |
| 14H | 30.66 | 1.2221 | 29.4379 | 30.66 | 1.2221 | 29.4379 | 30.628 | 1.2541 | 29.3739 |
| 16H | 31.0626 | 0.8195 | 30.2431 | 31.0626 | 0.8195 | 30.2431 | 31.0074 | 0.874 | 30.1334 |
| 17H | 30.2216 | 1.6605 | 28.5611 | 30.2216 | 1.6605 | 28.5611 | 30.1511 | 1.731 | 28.4201 |
| 18H | 29.2452 | 2.6369 | 26.6083 | 29.2452 | 2.6369 | 26.6083 | 29.191 | 2.6911 | 26.4999 |
| 19H | 31.0626 | 0.8219 | 30.2407 | 31.0602 | 0.8219 | 30.2383 | 31.064 | 0.8181 | 30.2459 |
| 20H | 32.0056 | -0.1235 | 32.1291 | 32.0056 | -0.1235 | 32.1291 | 31.9903 | -0.1082 | 32.0985 |
| 21H | 31.1101 | 0.772 | 30.3381 | 31.1101 | 0.772 | 30.3381 | 31.0941 | 0.788 | 30.3061 |
Table 4: Experimental and calculated 1H and 13C NMR chemical shifts (ppm) of propylbenzene.
In view of the range of 13C NMR chemical shifts for similar organic molecules usually is >100 ppm [27,28] the accuracy ensures reliable interpretation of spectroscopic parameters. In the present work, 13C NMR chemical shifts of some carbons in the chain are >100 ppm, as they would be expected in Table 5. In the case of Propylbenzene, the chemical shift of C1, C3, C3,C4, C5 and C6 are 81.21, 77.35, 86.13, 78.60, and 85.31 ppm, respectively. The shift is higher in C2, C12, C13 and C15 than rest of others.
| λ(nm) | E (eV) | ( f ) | Major contribution | Assignment | Region | Bands |
|---|---|---|---|---|---|---|
| Gas | ||||||
| 234.96 | 5.276 | 0.0048 | H→L (92%) | n→π* | Quartz UV | R-band (German, radikalartig) |
| 210.53 | 5.889 | 0.0162 | H→L (89%) | n→π* | Quartz UV | |
| 205.88 | 6.0220 | 0.0015 | H→L (86%) | n→π* | Quartz UV | |
| DMSO | ||||||
| 234.72 | 5.282 | 0.0082 | H→L-1 (90%) | n→π* | Quartz UV | R-band (German, radikalartig) |
| 210.99 | 5.876 | 0.0258 | H→L-1 (90%) | n→π* | Quartz UV | |
| 201.57 | 6.150 | 0.0022 | H→L-1 (87%) | n→π* | Quartz UV | |
| H+1→L-1 (83%) | σ→σ* | Quartz UV | ||||
| CCl4 | ||||||
| 235.13 | 5.273 | 0.0082 | H→L-1 (86%) | n→π* | Quartz UV | R-band (German, radikalartig) |
| 211.41 | 5.864 | 0.0252 | H→L-1 (85%) | n→π* | Quartz UV | |
| 204.13 | 6.0736 | 0.0020 | H→L-1 (78%) | n→π* | Quartz UV | |
| H+1→L-1(77%) | σ→σ* | Quartz UV | ||||
| Nitro methyl | ||||||
| 234.70 | 5.282 | 0.0080 | H+1→L (86%) | n→π* | Quartz UV | R-band (German, radikalartig) |
| 210.93 | 5.878 | 0.0252 | H+1→L-1 (85%) | n→π* | Quartz UV | |
| 201.59 | 6.150 | 0.002 | H→L-1 (78%) | n→π* | Quartz UV | |
| H+1→L-1(74%) | σ→σ* | Quartz UV | ||||
Table 5: Theoretical electronic absorption spectra of propylbenzene (absorption wavelength λ (nm), excitation energies E (eV) and oscillator strengths (f)) obtained using the TD-DFT/B3LYP/6-311++G(d,p) method.
The C3 in the chain has more shifted than other due to the delocalization of σ and π electrons. The shift of the entire carbons of the ring is found increased when going from gas to solvent due to the solvent effect. The shift values of carbons in DMSO phase are greater than Chloroform phase. The chemical shift values of oxygen have not changed due to the solvent effect. The experimental and theoretical 1H and 13C NMR chemical shift of Propylbenzene are presented in Table 5. This effect of isolation is the main cause to change the chemical property from benzene to Propylbenzene.
Optical properties (HOMO-LUMO analysis)
The UV and visible spectroscopy is used to detect the presence of chromophores in the molecule and whether the compound has NLO properties or not. The calculations of the electronic structure of Propylbenzene are optimized in singlet state. The low energy electronic excited states of the molecule are calculated at the B3LYP/6- 311++G(d,p) level using the TD-DFT approach on the previously optimized ground-state geometry of the molecule. The calculations are performed for Propylbenzenein gasphase and with the solvent of DMSO, CCl4, and Nitromethene. The calculated excitation energies, oscillator strength (f) and wavelength (λ) and spectral assignments are given in Table 6.
| f+ = (q+1)-q | f-=q-(q-1) | Δf=(f+)-(f-) | ΔS =Δfσgs | Δω=Δfωgei |
|---|---|---|---|---|
| -0.0990 | 5.5674 | -5.6665 | -64.971 | -0.3539 |
| 0.10410 | -1.0720 | 1.1761 | 13.4852 | 0.0734 |
| -0.0989 | 5.57436 | -5.6732 | -65.049 | -0.3544 |
| -0.0488 | -3.9275 | 3.8786 | 44.472 | 0.2422 |
| -0.1308 | 0.4939 | -0.6248 | -7.1641 | -0.0390 |
| -0.0487 | -3.9281 | 3.8793 | 44.480 | 0.2423 |
| -0.0636 | -3.1527 | 3.0890 | 35.419 | 0.1929 |
| 0.03984 | -0.0434 | 0.0832 | 0.9542 | 0.0051 |
| -1.1396 | -0.7127 | -0.4268 | -4.8945 | -0.0266 |
ΔS = local softness, σgs- global softeness; -Δω local electophilic index, ωgei- global
electrophilic index
Table 6: Fukui function and global and local softness, and electrophilicity index of propylbenzene.
TD-DFT calculations predict three transitions in the quartz ultraviolet region. In the case of gas phase, the strong transition is at 234.96, 210.53 and 205.88nm with an oscillator strength f=0.0048, 0.0162, 0.0015 with 5.2767 eV energy gap. The transition is n→π* in visible and quartz ultraviolet region. The designation of the band is R-band(German, radikalartig) which is attributed to above said transition of prophyl groups. They are characterizes by low molar absorptivities (ξmax<100) and undergo hypsochromic shift with an increase in solvent polarity. The simulated UV-Visible spectra in gas and solvent phase of Propylbenzene are shown in Figure 5.
In the case of DMSO solvent, strong transitions are 234.72, 210.99, 201.57 nm with an oscillator strength f=0.0082, 0.0258, 0.0022 nm with maximum energy gap 6.1509 eV.They are assigned to n → π* and σ→ σ*transitions and belongs to quartz ultraviolet region. This shows that, from gas to solvent, the transitions moved from visible to quartz ultraviolet region. This view indicates that, the Propylbenzene molecule having crystal property and thus, it is capable of having rich NLO properties. In addition to that, the calculated optical band gap 5.111 eV which ensure that the present compound has NLO properties. In view of calculated absorption spectra, the maximum absorption wavelength corresponds to the electronic transition from the HOMO to LUMO with maximum contribution.
The chemical hardness and potential, electronegativity and Electrophilicity index are calculated and their values are shown in Table 7. The chemical hardness is a good indicator of the chemical stability. The chemical hardness is decreased slightly (1.72-3.01) in going from Gas to solvent. Hence, the present compound has much chemical stability. Similarly, the electronegativity is increased from 3.45 upto 3.36, from Gas to solvent, if the value is greater than 1.7; the property of bond is changed from covalent to ionic. Accordingly, the bonds in the compound converted from covalent to ionic and are independent of solvent. Electrophilicity index is the measure of energy lowering due to maximal electron flow between donor [HOMO] and acceptor [LUMO]. From the Table 7, it is found that the Electrophilicity index of Propylbenzene is 3.45 in gas and 3.36 in solvent, which is moderate and this value ensure that the strong energy transformation between HOMO and LUMO.The dipole moment in a molecule is another important electronic property. Whenever the molecule has larger the dipole moment, the intermolecular interactions are very strong. The calculated dipole moment value for the title compound is 12.24 Debye in gas and 15.75 in solvent. It is too high which shows that; the Propylbenzene molecule has strong intermolecular interactions.
| Parameters | Gas | CCl4 | Nitromethene | DMSO |
|---|---|---|---|---|
| EHOMO (eV) | -6.63169 | -5.25427 | -6.824886218 | -6.82679 |
| ELUMO (eV) | -0.39865 | -0.4928 | -0.572527435 | -0.57443 |
| ΔEHOMO-LUMO gap (eV) | -6.23304 | -4.76147 | -6.252358783 | -6.25236 |
| Electronegativity (χ) | 3.5151 | 2.380736 | 3.126179391 | 3.126179 |
| Chemical hardness (η) | -3.11652 | -2.38074 | -3.126179391 | -3.12618 |
| Global softness (σ) | -0.32087 | -0.42004 | -0.319879276 | -0.31988 |
| Electrophilicity index (ω) | -1.98346 | -1.19037 | -1.563089696 | -1.56309 |
| Dipole moment (μ) | 15.44518 | 17.7527 | 21.17546183 | 20.47384 |
Table 7: HOMO, LUMO, Kubo gap, global electronegativity, global hardness and softness, global electrophilicity index of propylbenzene.
Global softness and local region-selectivity
Molecular charge distribution, molecular orbital surfaces and HOMO and LUMO energies have been used as reactivity descriptors in DFT study. The energy gap between the HOMO and LUMO orbital have been found to be adequate to study the stability and chemical reactivity of great variety of molecular system and is an important stability index. Besides the traditional reactivity descriptors there are a set of chemical reactivity descriptors which can be derived from DFT, such as global hardness (η), global softness, local softness (S), Fukui function (f) and global and local electrophilicity indexes (ω) [29-39]. These quantities are often defined by the Koopman’s theorem [40,41].
Electronegativity (χ) is the measure of the power of an electron or group of atoms to attract electrons towards itself [42] and according to Koopman’s theorem; it can be estimated by using the following equation:
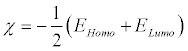 (1)
(1)
Where EHomo is the energies of the highest occupied molecular orbital (HOMO) and ELumo is the energy of the lowest unoccupied molecular orbital (LUMO).Global hardness (η) measures the resistance of an atom to a charge transfer [41] and it is estimated using the equation:
 (2)
(2)
Global softness (S) describes the capacity of an atom or group of atoms to receive electrons [43] and it is estimated by using the equation:
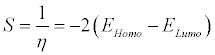 (3)
(3)
Where, η is the global hardness values. Global electrophilicity index (ω) is estimated by using the electronegativity and chemical hardness parameters through the equation:
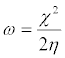 (4)
(4)
A high value of electrophilicity describes a good electrophile while a small value of electrophilicity describes a good nucleophile.
Fukui indices are a measurement of the chemical reactivity, as well as an indicator of the reactive regions and the nucleophilic and electrophilic behaviors of the molecule. The regions of a molecule where the Fukui function is large are chemically softer than the regions where the Fukui function is small, and by invoking HSAB principle in a local sense, one may establish the behavior of different sites with respect to hard or soft reagents. Condensed to atom Fukui function is reactive descriptor to identify nucleophilic and electrophilic attack site in candidate molecules, perhaps it is also used to recognize the electron acceptor center and donor centers. fk+ for any given site is positive then it is a preferred site for nucleophilic attack, on the contrary negative value implies electrophilic attack.
The Fukui function is defined as [44,45]:
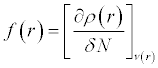 (5)
(5)
Where ρ(r) is the electron density and N
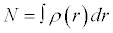 (6)
(6)
N is the number of electrons and r is the external potential exerted by the nucleus.
Phenyl ring gets activated at ortho and para positions as there are electron releasing substituent such as -OH, -NH2, -OR, R, etc. Propyl substituent in fact is an electron releasing substituent, consequently promotes the ortho and para positions for electrophilic attack a common reactivity trend observed in phenyl compounds. Local reactivity descriptors such as fk+,fk-, Δf, Δω for the different sites of phenyl ring are in conformity with the observed reactivity trend of the candidate molecule.
fk+,fk-, Δf, Δω unambiguously reveal the nucleophilic attack to be in the decreasing sequence asC6>C4 >C2 and that of electrophilic attack is found to be in the order C1>C3>C5 in the phenyl ring. This trend for attack of electrophile is in conformity with that of ΔS and Δω. The ortho and para positions show the tendency for attack of electrophile which is indeed a common trend observed in alkyl substituted phenyl ring compounds.
Molecular electrostatic potential (MEP) maps
The molecular electrical potential surfaces illustrate the charge distributions of molecules three dimensionally. This map allows us to visualize variably charged regions of a molecule. Knowledge of the charge distributions can be used to determine how molecules interact with one another and it is also be used to determine the nature of the chemical bond.Molecular electrostatic potential is calculated at the B3LYP/6-311+G(d,p) optimized geometry [46,47]. There is a great deal of intermediary potential energy, the non red or blue regions indicate that the electro negativity difference is not very great. In a molecule with a great electro negativity difference, charge is very polarized, and there are significant differences in electron density in different regions of the molecule. This great electro negativity difference leads to regions that are almost entirely red and almost entirely blue [48]. Greater regions of intermediary potential, yellow and green, and smaller or no regions of extreme potential, red and blue, are key indicators of a smaller electronegativity.
The color code of these maps is in the range between -6.15 a.u. (Deepest red) to 6.15 a.u. (deepest blue) in compound. The positive (blue) regions of MEP are related to electrophilic reactivity and the negative (green) regions to nucleophilic reactivity shown in Figure 6. From the MEP map of the candidate molecule the red regions of the molecule found to be ready for electrophilic attack, and especially in the phenyl ring the atoms are clouded with red colour. From the findings of the Fukui local reactivity descriptor the atoms C1, C3 and C5 are nucleophile ready for electrophilic attack and atoms C2, C4 and C6 are the regions for nucleophilic attack. Molecular electrostatic potential map can be confirmed with the finding of the Fukui descriptors.
In order to investigate the relationships among molecular structures and non-linear optic properties (NLO), the polarizabilities and first order hyperpolarizabilities of the Propylbenzene compound was calculated using DFT-B3LYP method and 6-311+G(d,p) basis set, based on the finite-field approach.
The Polarizability and hyperpolarizability tensors (Table 8) (αxx, αxy, αyy, αxz, αyz, αzz and βxxx, βxxy, βxyy, βyyy, βxxz, βxyz, βyyz, βxzz, βyzz, βzzz) can be obtained by a frequency job output file of Gaussian. However, α and β values of Gaussian output are in atomic units (a.u.). So they have been converted into electronic units (esu) (α; 1 a.u.=0.1482×10−24esu, β; 1 a.u.=8.6393×10−33 esu). The calculations of the total molecular dipole moment (μ), linear polarizability (α) and first-order hyperpolarizability (β) from the Gaussian output have been explained in detail previously [49,50] and DFT has been extensively used as an effective method to investigate the organic NLO materials [51-55].
| Parameter | a.u. | Parameter | a.u. |
|---|---|---|---|
| αxx | - 53.3963 | βxxx | 13.79 |
| αxy | -0.2807 | βxxy | 0.9912 |
| αyy | -52.6869 | βxyy | 3.7575 |
| αxz | -0.9506 | β yyy | 0.8982 |
| αyz | -0.2339 | βxxz | 0.4223 |
| αzz | -59.5384 | βxyz | 0.6611 |
| αot | -55.2072 | βyyz | -0.7173 |
| Δα | 6.695 | βxzz | -9.9781 |
| μx | -0.5586 | βyzz | -1.0315 |
| μy | - 0.0696 | βzzz | 1.4772 |
| μz | 0.0731 | βtot | 2.940 |
| μot | 0.1611 |
Table 8: The electronic dipole moment (μ) (Debye), polarizability (α) and first hyperpolarizability (β) of propylbenzene.
 (7)
(7)
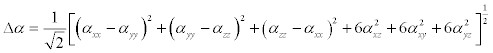 (8)
(8)
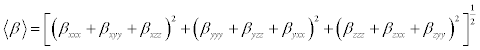 (9)
(9)
In Table 7, the calculated parameters described above and electronic dipole moment {μi(i = x, y, z) and total dipole moment μtot } for title compound are listed. The total dipole moment was calculated using the following equation [56].
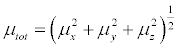 (10)
(10)
It is well known that, molecule with high values of dipole moment, molecular Polarizability, and first hyperpolarizability having more active NLO properties. The first hyperpolarizability (β) and the component of hyperpolarizability βx, βy and βz of Propylbenzene along with related properties (μ0, αtotal, and Δα) are reported in Table 6. The calculated value of dipole moment is found to be 0.16111 Debye. The highest value of dipole moment is observed for component μX. In this direction, this value is equal to 0.0731 D. The lowest value of the dipole moment of the molecule compound is μY component (-0.0696 D). The calculated average Polarizability and anisotropy of the Polarizability is -55.2077×10-24 esu and 6.6956×10−24 esu, respectively. The magnitude of the molecular hyperpolarizability β, is one of important key factors in a NLO system. The B3LYP/6-311+G(d,p) calculated first hyperpolarizability value (β) is 2.9780×10−30 esu. From the above results, it is observed that, the molecular Polarizability and hyperpolarizability of the title compound in all coordinates are active. So that, the Propylbenzene can be used to prepare NLO crystals and those crystal is able to produce second order harmonic waves.
In the present investigation, FT-IR, FT-Raman and 13C NMR and 1H NMR spectra of the Propylbenzene were recorded and the observed vibrational frequencies were assigned depending upon their expected region. The chronological change of finger print and group frequency region of the amino acid with respect to the functional group has also monitored. The change of geometrical parameters along with the substitutions was deeply analyzed. The simulated 13C NMR and 1H NMR were compared with the recorded spectrum and the chemical shifts related to TMS were studied. The change of chemical properties of the molecule by the substitutions has been analysed. The electrical and optical properties of the Propylbenzene were profoundly investigated using frontier molecular orbital (Figure 7). From the UVVisible spectra, it was found that the present compound was optically active and posses NLO properties. The molecular electrostatic potential (MEP) map was performed and from which the change the chemical properties of the compound was also discussed. The possible sites of nucleophilic and electrophilic attacks in the molecule were determined through local reactivity and Fukui condensed softness indices.