
Biochemistry & Pharmacology: Open Access
Open Access
ISSN: 2167-0501
+44-77-2385-9429

ISSN: 2167-0501
+44-77-2385-9429
Research Article - (2015) Volume 4, Issue 4
Vibrational characteristics of 2- nitrophenol have been investigated using experimental IR and Raman data and computational data using DFT method employing the 6-311++G** basis set available on Gaussian-09 software for the most stableconformer C-1. Complete vibrational assignments of the experimental IR and Raman bands have been proposed in light of the results obtained from the DFT computations and the PEDs computed using GAR2PED software. The optimized geometrical parameters suggest that the overall symmetry of the most stablemolecule is Cs. The molecule is expected to have three conformers. In the present article all the characterizations and the analyses of the lowest energy conformer of 2-NP have been studied. The charge transfer occurring in the molecule has been shown by HOMO–LUMO energy orbitals the energy gap of HOMO LUMO orbitals have been found 4.03eV. The mappings of electron density iso-surface with the electrostatic potential (ESP), has been carried out to get the information about the size, shape, charge density distribution and site of chemical reactivity of 2-NP. Current density and magnetic shielding of C-1 have been investigated. Some essential thermo molecular characteristics, namely, enthalpy, Gibb’s free energy, thermal energy, entropy, heat capacity, internal energy and the partition functions of the molecule have also been analyzed.
<Keywords: Optimized structure; Conformers; Entropy; MESP; Magnetic shielding; 2-nitro-phenol
Nitro phenols constitute a class of volatile organic compounds that is increasingly presented in urban as well as in natural environments [1-3]. These are important and versatile compounds in the industrial, agricultural and defence applications [4] and are frequently used as intermediates in the manufacture of explosives, pharmaceuticals, pesticides, pigments, dyes, rubber chemicals, lumber preservatives, photographic chemicals, etc. [5-8]. 2- Nitro-phenols (2-NP), in particular, poses significant health risks since it is a toxic to mammals, microorganisms and anaerobic bacteria. Its toxicity is thought to be due to the nitro group being easily reduced by the enzymes into nitro anion radical, nitroso and hydroxylamine derivatives [4]. Although extensive experimental and theoretical studies are reported on the structural and vibrational studies of mono-substituted phenols [9,10] dealing with their structural features, intra-molecular H-bonding parameters and the vibrational spectra [11-14], only few works of this kind exist on phenols [15-18]. In the present study we report the results of our probing into the application of the DFT based SQM method [19] to the vibrational analysis of hydrogen bonded systems. The main difficulty in such investigations is that the vibrational spectra of these compounds have not been completely analyzed even now and generally only rough assignments are available. Therefore, an investigation of the performance of the DFT-based SQM method has to be carried out simultaneously with a complete vibrational analysis of the molecule. This process was done successfully in the case of 2 6-difluorophenol earlier [20].
The 2-NP molecule, contains a strong intra-molecular (O) H......O(N) hydrogen bonding interaction which has been analyzed by various experimental and theoretical studies [21-31]. The extensive investigations corresponding to the vibrational description of 2-NP is not complete. Most of the numerous spectroscopic studies [24,31-33] focused on the vibrations from which the information can be carried out about the hydrogen bonding interaction, first of all on the OH stretching and OH torsion.
In the present work calculations have been made for the optimized molecular geometries, APT and Mulliken atomic charges and the fundamental vibrational wave numbers along with their intensities in the IR spectrum, Raman activities and the depolarization ratios of the Raman lines using the DFT (B3LYP) method employing the 6-311++G** basis set [34-38] available with Gaussian-09 software [39] for the lowest energy conformer C-1 of 2- NP. The experimental IR and Raman spectral data have been analyzed in the light of the computed fundamentals and the corresponding PEDs calculated, using the GAR2PED software [40]. For the calculation of the PEDs the vibrational problem was set up in terms of the internal coordinates for the GAR2PED software. HOMOLUMO, total density plots, electrostatic potential (ESP) surface and their arrays have been investigated. The essential NLO as well as thermo molecular parameters have been investigated and using NMR analysis employing Continuous Set of Gauge Transformation (CSGT) method electro-magnetic characteristics of 2-NP have been investigated.
One to two milligrams of the pure (98%), a yellow crystalline solid in powdered form, 2-nitro phenol, purchased from Sigma Aldrich Chemical Co. (USA), was used to record the Raman spectra using a home assembled micro-Raman spectrometer: Horiba Jobin-Yuon Spectrometer (iHR-320) system with an inverted microscope (Nikon Eclipse Ti-U, Japan). A Diode laser (Star bright Diode Laser, Torsana Laser Tech, Denmark) of λ=785 nm used as source to illuminate the sample sandwiched between quartz cover slip and borosilicate glass slide. The sample was mounted on the microscope stage and a 60X microscope objective have been used to focus the laser beam and to record the Raman signals. A liquid Nitrogen cooled Symphony CCD detector have been utilized to collect the Raman scattered radiation. The spectral range of the micro-Raman have been kept 200-3100 cm-1 with resolution 5 cm-1, accuracy 2 cm-1 at spectrometer slit width 100 μm. In order to record a better Raman spectrum, data were obtained using a laser power of 47mW with the acquisition times of 5 min.
FTIR spectrum of 2-NP sample was recorded using KBr pellet. The 10 mg of the 2-NP sample was weighed and properly mixed with 990 mg KBr. This mixture was then pelleted using KBr pellet maker by applying pressure using 8 tons weight for half an hour. FTIR spectrum was recorded using the above mentioned pellet at room temperature, using an FTIR spectrometer (Jasco 6300) with a standard source. The spectra have been recorded in the range of 400- 4000 cm-1. The 200 scans have been taken with 2 cm-1 spectral resolution for all the three samples.
To optimize the structure of 2- NP the following procedure was adopted. Initially the benzene ring (including H atoms only) was optimized. After this an OH group was added to a carbon atom of benzene ring and the structure was optimized. With this structure a nitro group was added to the ortho position of phenolic group (Figure 1).
This structure was further optimized. In the optimized structure if hydrogen atom of the OH group faces the NO2 group the structure remains planar. However, if the hydrogen atom of the OH group is kept away from the NO2 group there are two possible conformers of 2-NP, in one conformer the plane of NO2 makes the angle -33.70 while in the other it makes an angle of 33.70 with the plane of phenyl ring (Figure 2).
Therefore total 3 possible conformers have been found to exist of the 2-NP molecule. The energies of all the three optimized conformers are -512.12911314 (C-1), -512.11232617 (C-2) and -512.10755721(C-3) a.u. (Table 1). In the present paper we have considered the vibrational characteristics of the most stableconformer C-1 only.
| Conformers | Point group | Total energy (Hartree) | Relative energy | ||
|---|---|---|---|---|---|
| Hartree | Temp. (K) | kcal/mol | |||
| C-1 | Cs | -512.12911314 | 0 | 0 | 0 |
| C-2 | C1 | -512.11232617 | 0.01678697 | 5300.9405365 | 10.533984965 |
| C-3 | C1 | -512.10755721 | 0.02155593 | 6806.868848 | 13.52655319 |
Table 1: Total and relative energies of all the possible conformers of 2- NP.
The optimized molecular geometries, APT charges and the fundamental vibrational wave numbers along with their corresponding intensities in IR spectrum, Raman activities and the depolarization ratios of the Raman bands for the present molecule were computed at the B3LYP/6-311++G** level using the Gaussian 09 program package. The unscaled B3LYP/6-311++G** vibrational frequencies are generally slightly larger than the experimental values. In order to achieve the reasonable frequency matching, the scale factors proposed by Rauhut and Pulay [42] were employed. The assignments of all the normal modes of vibration have been made on the basis of the computed PEDs. The experimental IR and Raman frequencies corresponding to the fundamental modes have been compared with the calculated fundamental frequencies in light of the PEDs. The molecular electrostatic potential (ESP) surface, used for the predicting sites and relative reactivity towards the electrophilic attack and in the studies of biological recognition and hydrogen bonding interactions, has been plotted and the complete thermo-molecular data analysis, complete description of global reactivity parameters and essential features of electro-magnetism of 2-NP have been investigated.
Molecular geometries
The geometrical parameters of 2-NP computed at the B3LYP/6- 311G** level of theory are compared with the experimental and MP2/6- 31G* data in Table 2. The optimized geometrical structure of 2-NP has overall Cs symmetry for the lowest energy conformer. The computed O–H and N–O bond lengths are larger compared with the experimental values. At the same time, the C–O and C–N bond lengths seem to be somewhat shorter. These geometrical parameters are sensitive to hydrogen bonding [15]. Taking into account the above considerations, the data (Table 2) show good agreement between the experimental and theoretical geometries with some minor discrepancies. The computed O–H and N–O bond lengths are larger compared to the experimental values. The computed bond angles are consistent at both levels (Electron Diffraction and MP2/6-31G*) of theory; the deviations from the experimental values are within or close to experimental error.
| S.No. | Parameters | B3-LYP/6-311++G** | ED@ | MP2(FC) / 6-31G*@ | ||
|---|---|---|---|---|---|---|
| C-1$,# | C-2# | C-3# | ||||
| 1 | r(C1-C2) | 1.382 | 1.389 | 1.389 | 1.388 | 1.387 |
| 2 | r(C1-C6) | 1.404 | 1.396 | 1.396 | 1.399 | 1.402 |
| 3 | r(C1-H7) | 1.084 | 1.084 | 1.084 | 1.089 | 1.086 |
| 4 | r(C2-C3) | 1.404 | 1.400 | 1.400 | 1.406 | 1.405 |
| 5 | r(C2-H8) | 1.083 | 1.086 | 1.086 | 1.089 | 1.086 |
| 6 | r(C3-C4) | 1.415 | 1.405 | 1.405 | 1.411 | 1.410 |
| 7 | r(C3-O11) | 1.336 | 1.352 | 1.352 | 1.359 | 1.351 |
| 8 | r(C4-C5) | 1.402 | 1.393 | 1.393 | 1.402 | 1.401 |
| 9 | r(C4-N13) | 1.453 | 1.473 | 1.473 | 1.464 | 1.456 |
| 10 | r(C5-C6) | 1.380 | 1.387 | 1.387 | 1.387 | 1.386 |
| 11 | r(C5-H9) | 1.081 | 1.082 | 1.082 | 1.089 | 1.086 |
| 12 | r(C6-H10) | 1.082 | 1.082 | 1.082 | 1.089 | 1.086 |
| 13 | r(O11-H12) | 0.982 | 0.964 | 0.964 | 0.969 | 0.986 |
| 14 | r(N13-O14) | 1.219 | 1.221 | 1.221 | 1.225 | 1.239 |
| 15 | r(N13-O15) | 1.248 | 1.228 | 1.228 | 1.241 | 1.255 |
| 16 | α(C2-C1-C6) | 121.031 | 120.5 | 120.5 | 122.9 | 120.5 |
| 17 | α (C2-C1-H7) | 119.217 | 119.3 | 119.3 | -- | -- |
| 18 | α (C6-C1-H7) | 119.752 | 120.2 | 120.2 | -- | -- |
| 19 | α (C1-C2-C3) | 120.786 | 121.0 | 121.0 | 118.1 | 121.1 |
| 20 | α (C1-C2-H8) | 121.644 | 120.2 | 120.2 | -- | -- |
| 21 | α (C3-C2-H8) | 117.570 | 118.8 | 118.8 | -- | -- |
| 22 | α (C2-C3-C4) | 117.659 | 117.8 | 117.8 | 119.4 | 117.4 |
| 23 | α (C2-C3-O11) | 117.741 | 122.0 | 122.0 | -- | -- |
| 24 | α (C4-C3-O11) | 124.600 | 120.2 | 120.2 | 123.9 | 125.6 |
| 25 | α (C3-C4-C5) | 121.165 | 121.1 | 121.1 | 121.4 | 121.7 |
| 26 | α (C3-C4-N13) | 120.816 | 121.5 | 121.5 | 120.8 | 121.0 |
| 27 | α (C5-C4-N13) | 118.019 | 117.4 | 117.4 | -- | -- |
| 28 | α (C4-C5-C6) | 119.999 | 120.3 | 120.3 | 119.0 | 119.6 |
| 29 | α (C4-C5-H9) | 118.254 | 118.2 | 118.2 | -- | -- |
| 30 | α (C6-C5-H9) | 121.747 | 121.5 | 121.5 | -- | -- |
| 31 | α (C1-C6-C5) | 119.360 | 119.2 | 119.2 | 119.3 | 119.7 |
| 32 | α (C1-C6-H10) | 120.505 | 120.7 | 120.7 | -- | -- |
| 33 | α (C5-C6-H10) | 120.135 | 120.1 | 120.1 | -- | -- |
| 34 | α (C3-O11-H12) | 107.393 | 109.5 | 109.5 | 104.4 | 106.8 |
| 35 | α (C4-N13-O14) | 119.320 | 118.1 | 118.1 | 118.2 | 118.4 |
| 36 | α (C4-N13-O15) | 117.914 | 116.9 | 116.9 | 118.6 | 118.8 |
| 37 | α (O14-N13-O15) | 122.766 | 124.9 | 124.9 | 123.3 | 122.8 |
| 38 | δ(C6-C1-C2-C3) | 0.004 | 0.8 | -0.8 | -- | -- |
| 39 | δ(C6-C1-C2-H8) | 179.999 | -179.0 | 179.0 | -- | -- |
| 40 | δ(H7-C1-C2-C3) | 179.997 | -179.6 | 179.6 | -- | -- |
| 41 | δ(H7-C1-C2-H8) | -0.008 | 0.6 | -0.6 | -- | -- |
| 42 | δ(C2-C1-C6-C5) | -0.011 | 0.0 | -0.0 | -- | -- |
| 43 | δ(C2-C1-C6-H10) | 180.001 | 179.9 | -179.9 | -- | -- |
| 44 | δ(H7-C1-C6-C5) | -180.004 | -179.7 | 179.8 | -- | -- |
| 45 | δ(H7-C1-C6-H10) | 0.008 | 0.2 | -0.2 | -- | -- |
| 46 | δ(C1-C2-C3-C4) | -0.004 | -0.4 | 0.4 | -- | -- |
| 47 | δ(C1-C2-C3-O11) | -180.000 | -178.4 | 178.4 | -- | -- |
| 48 | δ (H8-C2-C3-C4) | -179.999 | 179.4 | -179.4 | -- | -- |
| 49 | δ (H8-C2-C3-O11) | 0.004 | 1.4 | -1.4 | -- | -- |
| 50 | δ (C2-C3-C4-C5) | 0.011 | -0.8 | 0.8 | -- | -- |
| 51 | δ (C2-C3-C4-N13) | -180.029 | 179.3 | -179.3 | -- | -- |
| 52 | δ (O11-C3-C4-C5) | 180.007 | 177.3 | -177.3 | -- | -- |
| 53 | δ (O11-C3-C4-N13) | -0.033 | -2.7 | 2.7 | -- | -- |
| 54 | δ (C2-C3-O11-H12) | 180.028 | 2.2 | -2.1 | -- | -- |
| 55 | δ (C4-C3-O11-H12) | 0.032 | -175.8 | 175.9 | -- | -- |
| 56 | δ (C3-C4-C5-C6) | -0.018 | 1.5 | -1.5 | -- | -- |
| 57 | δ (C3-C4-C5-C9) | -180.007 | -178.6 | 178.6 | -- | -- |
| 58 | δ (N13-C4-C5-C6) | 180.020 | 178.5 | 178.5 | -- | -- |
| 59 | δ (N13-C4-C5-H9) | 0.031 | 1.4 | -1.4 | -- | -- |
| 60 | δ (C3-C4-N13-O14) | 180.052 | -33.7 | 33.7 | -- | -- |
| 61 | δ (C3-C4-N13-O15) | 0.050 | 147.8 | -147.8 | -- | -- |
| 62 | δ (C5-C4-N13-O14) | 0.013 | 146.3 | -146.3 | -- | -- |
| 63 | δ (C5-C4-N13-O15) | 180.011 | -32.1 | 32.1 | -- | -- |
| 64 | δ (C4-C5-C6-C1) | 0.017 | -1.1 | 1.1 | -- | -- |
| 65 | δ (C4-C5-C6-H10) | -179.994 | 179.0 | -179.0 | -- | -- |
| 66 | δ (H9-C5-C6-C1) | 180.006 | 179.0 | -179.0 | -- | -- |
| 67 | δ (H9-C5-C6-H10) | -0.006 | -0.9 | 0.9 | -- | -- |
Table 2: Computed and observed geometrical parameters of 2- NP.
The bond lengths of C1-C2, C3-O11, C4-N13 and C5-C6 respectively are shorter while those lengths of C1-C6, C2-C3, C3-C4, C4-C5 and O11-H12 respectively are found to be larger in the most stableconformer than both the C-1 and C-2 conformers. Also, angle α (C4-C3-O11) is found to be larger while angle α (O14-N13-O15) is found to be shorter in the most stableconformer than the other two (Table 2). These conformational discrepancies may be due to intra-molecular hydrogen bonding in the most stableconformer and also due to instability of conformers C-2 and C-3 respectively.
APT charges
Atomic polarizability tensor (APT) charge is interpreted as the sum of charge tensor and charge flux tensor, leading to a charge-charge flux model [43,44]. The APT atomic charges (in unit of e) at various atomic sites of 2-NP are collected in Table 3. The carbon atoms belonging to the ring have alternately positive and negative APT charges with different magnitudes. All the H and N atoms have positive APT charges with different magnitudes, while the O atoms possess negative and different magnitudes of APT charges. The N atom possesses the highest magnitude which is connected directly to the ring and the two O atoms. It is also noticeable that the magnitude of the APT charge on C3 attached to the OH group is the largest of all the C atoms. Also, it is interesting to note that the N atom possesses positive APT charge. The magnitude of the APT charge on H12 is the largest of all the H atoms. The O atoms possess almost equal APT charges.
| Atoms | APT charges | Mulliken atomic charges | ESP charges | ESP Potentials | ||||
|---|---|---|---|---|---|---|---|---|
| (C-1) | (C-2/C-3) | (C-1) | C-2/C-3) | (C-1) | C-2/C-3) | C-1 | C-2/C-3) | |
| C1 | 0.168082 | 0.109390 | -0.251868 | -0.187756 | -0.087841 | -0.070392 | -14.73524 | -14.73734 |
| C2 | -0.168431 | -0.166562 | -0.165953 | 0.112368 | -0.242264 | -0.276459 | -14.74573 | -14.73986 |
| C3 | 0.617390 | 0.569682 | -0.630033 | -0.280495 | 0.387901 | 0.311740 | -14.66298 | -14.66522 |
| C4 | -0.369569 | -0.186726 | 0.559561 | -0.248181 | -0.069178 | 0.011254 | -14.69304 | -14.70101 |
| C5 | 0.098974 | 0.070105 | 0.139598 | 0.278052 | -0.166961 | -0.210985 | -14.73417 | -14.73785 |
| C6 | -0.238821 | -0.186101 | -0.249269 | -0.259811 | -0.137599 | -0.132966 | -14.74581 | -14.74815 |
| H7 | 0.051609 | 0.049260 | 0.175404 | 0.172879 | 0.138456 | 0.134908 | -1.07628 | -1.07627 |
| H8 | 0.067916 | 0.037818 | 0.205976 | 0.138330 | 0.181123 | 0.149018 | -1.07645 | -1.06388 |
| H9 | 0.102578 | 0.094642 | 0.239102 | 0.231315 | 0.166468 | 0.186660 | -1.07216 | -1.07586 |
| H10 | 0.049672 | 0.048614 | 0.185472 | 0.174564 | 0.136537 | 0.133989 | -1.08086 | -1.08272 |
| O11 | -0.726207 | -0.645764 | -0.185498 | -0.177027 | -0.590398 | -0.522159 | -22.31645 | -22.30600 |
| H12 | 0.390488 | 0.297918 | 0.290132 | 0.270747 | 0.471626 | 0.417133 | -0.95701 | -0.94374 |
| N13 | 1.350233 | 1.219919 | -0.296760 | -0.207132 | 0.681548 | 0.736291 | -18.13866 | -18.15683 |
| O14 | -0.688853 | -0.677157 | 0.004956 | -0.034067 | -0.388638 | -0.452560 | -22.32424 | -22.34426 |
| O15 | -0.705060 | -0.635038 | -0.020819 | 0.016214 | -0.480781 | -0.415470 | -22.32304 | -22.34320 |
Table 3: APT, Mulliken and ESP fitted (MK scheme) atomic charges and molecular electrostatic potentials at different atomic sites of 2-NP (C-I).
Mulliken atomic charges
Mulliken atomic charge calculation plays an important role in the application of quantum chemical calculation to molecular systems, because the atomic charges affect the dipole moment, polarizability, electronic structure, and much more properties of the molecular systems. Mulliken atomic charges (in unit of e) at various atomic sites of 2-NP are collected in Table 3 from which it can be noticed that all the carbon atoms except C4 and C5, have negative Mulliken atomic charges. One of the O atoms attached to the N atom with a single bond possesses positive Mulliken atomic charge. However, it is an electronegative atom like N and O atoms. The H atoms possess positive Mulliken atomic charge. The Mulliken atomic charge at the C atom attached to the OH group is the largest of all the C atoms and the H atom of the OH group possesses the largest Mulliken atomic charge of all the H atoms in the C-1 conformer.
ESP charges
The studies of effective atomic charges play a crucial role in the application of quantum mechanical computations to the molecular systems. Despite the conceptual problems associated with the dividing up overall molecular charge density in atomic contributions, and all the conventional problems related to the finding of convenient and robust algorithm applicable to a wide range of the systems [45]. The beauty of effective atomic charges as the parameters for the calculation of electrostatic interactions in a various molecular mechanics simulation packages is certainly one essential area of application. Partial atomic charges play a different, but even more important, role in the qualitative rationalization of organic and inorganic reactivity [46]. The molecular electrostatic potential (ESP) derived charges are those are reproduced by fitting the partial atomic charges to reproduce the molecular electrostatic potential (MEP) at a number of points around the molecule at a (large) number of grid points using Merge-Singh- Kollman (MK) scheme [47].
The molecular ESP derived charges at various atomic sites of 2-NP have been contained in the Table 3. Clearly, the ESP charges at all the C atoms except C3, have negative and small but different value while C3 atom, attached to OH group of 2-NP, have positive and largest value amongst all the C atoms of 2-NP. All the H atoms on the ring possess smaller but positive ESP charges while H atom of OH group attains positive and largest value of all the H atoms in the molecule. The O atoms possess negative ESP charges. The O atom of OH group attains largest negative value (-0.590398 e) while N atom of NO2 group attains largest positive value (0.681548 e) of ESP charges in 2-NP.
Vibrational assignments
The 2-NP molecule is a 15 atomic molecule with 39 normal modes of vibration in which 30 modes are associated with the benzene ring which are : 12 stretching modes -ν, 3 planar ring deformation -α(R), 3 non planar ring deformation -Φ(R), 6 planar deformation modes -β(C-H) and 6 non-planar deformation modes -γ(C-H),out of which 2 of each i.e. β(C-H) and γ(C-H) become β(C-N), β(C-O) and γ(C-N), γ(C-O) respectively. The three normal modes of OH-group are: OH stretching -ν(OH), OH torsion -τ(OH) and C-O-H angle bending. The six normal modes of the nitro group are: anti-symmetric NO2 stretching -νas(NO2), symmetric NO2 stretching -νs(NO2), NO2 rocking -ρ(NO2), NO2 wagging -ω(NO2), NO2 scissoring -δ(NO2) and NO2 torsion -τ(NO2).
The calculated and observed vibrational frequencies along with the corresponding PEDs and vibrational assignments are collected in Table 4. The experimental and calculated IR and Raman spectra are reproduced in Figure 3-6. The normal mode assignments have been discussed under the following sections: (i) The phenyl ring modes (30), (ii) The OH group modes (3) and (iii) The NO2 group modes (6).
| t | Calculated Frequencies (cm-1) | Observed Freq @. (cm-1) | PEDs | Mode Assigned | ||||
|---|---|---|---|---|---|---|---|---|
| [41] | Our work | |||||||
| Sc. | Unsc. | Raman | IR | Raman | IR | |||
| ν1 | 3453 | 3471 (241,108)0.14 | -- | 3253 | -- | 3358 | ν (O11-H12) (100) | n (O-H) |
| ν2 | 3205 | 3222 (4,94)0.16 | -- | 3115* | -- | -- | ν (C5-H9) (91) + ν (C6-H10) (8) | ν (C-H) |
| ν3 | 3186 | 3203 (2,170)0.12 | -- | 3099 | -- | -- | ν (C2-H8) (67) + ν (C1-H7) (17) + ν (C6-H10) (12) | n (C-H) |
| ν4 | 3181 | 3197 (5,88)0.62 | -- | 3091 | -- | 3136 | ν (C6-H10) (67) + ν (C2-H8) (23) | ν (C-H) |
| ν5 | 3034 | 3178 (4,73)0.65 | 3100 | 3060 | -- | 3065 | ν (C1-H7) (78)+ν (C6-H10) (13)+ ν(C2-H8) (9) | ν (C-H) |
| ν6 | 1586 | 1661 (133,9)0.75 | 1615 | 1625 | -- | 1600 | ν (C3-C4) (15) + ν (C1-C6) (13) + ν (C4-C5) (13) + ν (C1-C2) (13) +ν (N13-O14) (6)+ α3 (R) (9) | ν (R) |
| ν7 | 1547 | 1620 (81,31)0.56 | 1600 | 1603 | 1582 | 1559 | ν (C5-C6) (21) + ν (C2-C3) (18) + ν (C1-C2) (7) + ν (C4-C5) (6) + ν (C3-C4) (6) + α (C3-O11-H12) (10) + α2 (R) (9) | ν (R) |
| ν8 | 1511 | 1582 (163,37)0.60 | 1540 | 1550 | 1525 | 1501 | νas (NO2) (52) +n (C1-C2) (8) + n (C3-C4) (7) + β (C4-N13) (8) + ρ (NO2) (8) | νas (NO2) |
| ν9 | 1442 | 1510 (119,2)0.30 | 1465 | 1476 | -- | 1462 | ν (C3-O11) (13) + ν (C1-C6) (11) +ν (C2-C3) (9) + ν (C4-C5) (7) + β (C1-H7) (11) + β (C5-H9) (13) + β (C2-H8) (17) | ν (C-O) |
| ν10 | 1420 | 1487 (107,8)0.44 | -- | 1460* | 1453 | 1423 | ν (C1-C6) (12) + ν (C4-C5) (4) + ν (C3-C4) (3) + νas (NO2) (26) + β (C6-H10) (20)+ α (C3-O11-H12) (6) | ν (R) |
| ν11 | 1349 | 1413 (68,40)0.16 | 1398 | 1380 | 1366 | 1404 | α (C3-O11-H12) (28)+ ν (C3-C4) (10) + ν (C1-C2) (9) + ν (C1-C6) (8) + ν (C2-C3) (6)+ νs (NO2) (9) + β (C1-H7) (9) + β (C5-H9) (7) | α (C-O-H) |
| ν12 | 1306 | 1368 (86,3)0.53 | 1319 | 1333* | 1348 | ν (C3-C4) (15)+ν (C5-C6) (11)+ν (C1-C2) (10)+ν (C4-C5) (5)+ν (C2-C3) (4)+ν (C3-O11) (13) + β (C2-H8) (13) + β (C6-H10) (8) | ν (R) | |
| ν13 | 1260 | 1319 (218,77)0.30 | 1252 | 1325* | 1234 | -- | β (C5-H9) (13) + ν (N13-O15) (22) +ν (C1-C6) (9) + ν (C5-C6) (9) + α (C3-O11-H12) (12) + ν (C4-N13) (8) + δ (NO2) (6) + ν (C3-O11) (6) | β (C-H) |
| ν14 | 1226 | 1284 (175,98)0.23 | 1198 | 1256* | 1181 | 1284 | νs (NO2) (24) + ν (C3-O11) (22) +ν (C4-C5) (9) + ν (C1-C6) (7) + β (C1-H7) (7) + δ (NO2) (7) | νs (NO2) |
| ν15 | 1177 | 1232 (107,42)0.22 | 1160 | 1201 | 1158 | 1209 | β (C2-H8) (19) +ν (C4-C5) (10) + ν (C5-C6) (8) + ν (C1-C6) (5) + α (C3-O11-H12) (17) + β (C5-H9) (10) + ν (C4-N13) (7) | β (C-H) |
| ν16 | 1131 | 1185 (10,3)0.61 | 1145 | 1165 | 1136 | -- | β (C6-H10) (43) + β (C5-H9) (18) +ν (C1-C2) (11) + ν (C2-C3) (5) + β (C1-H7) (12) | β (C-H) |
| ν17 | 1106 | 1158 (41,32)0.33 | 1113 | 1140 | 1117 | 1146 | ν (C3-C4) (9) + ν (C1-C6) (8) + ν (C1-C2) (8) +β (C5-H9) (25) + β (C2-H8) (19) + ν (C4-N13) (11) | ν (R) |
| ν18 | 1051 | 1101 (28,4)0.14 | 1094 | 1080 | -- | 1092 | ν (C4-C5) (13) + ν (C4-N13) (22) + α1 (R) (32) + β (C5-H9) (9) | ν (R) |
| ν19 | 1002 | 1049 (14,26)0.04 | 1055 | 1030 | 1026 | 1040 | ν (C2-C3) (47) + ν (C3-C4) (13) + ν (C1-C2) (7) + β (C2-H8) (10) + β (C5-H9) (8) | ν (R) |
| ν20 | 978 | 1000 (0,0)0.75 | 1022 | 981* | -- | 1002 | γ (C1-H7) (51) + γ (C6-H10) (18) + γ (C2-H8) (14) + Φ1 (R) (11) | γ (C-H) |
| ν21 | 956 | 977 (2,0)0.75 | 998 | 954 | -- | 973 | γ (C5-H9) (53) + γ (C6-H10) (21) + γ (C2-H8) (11) + Φ2 (R) (7) + γ (C1-H7) (6) | γ (C-H) |
| ν22 | 865 | 884 (17,4)0.18 | 883 | 871 | 867 | 882 | α1 (R) (37) + α3 (R) (8) + δ (NO2) (29) + ν (C4-N13) (7) + ν (C3-O11) (6) | α (R) |
| ν23 | 849 | 868 (0,0)0.75 | -- | 860* | -- | -- | γ (C2-H8) (49)+γ (C5-H9) (17)+γ (C6-H10) (9) + γ (C3-O11) (7) + Φ1 (R) (6) + γ (C1-H7) (6) | γ (C-H) |
| ν24 | 819 | 837 (9,35)0.07 | 817 | 820 | 818 | 832 | δ (NO2) (32) +ν (C5-C6) (12) + ν (C4-C5) (10) + ν (C1-C6) (5) + ν (C3-O11) (11) + α1 (R) (8) + α3 (R) (6) | δ (NO2) |
| ν25 | 760 | 777 (48,0)0.75 | -- | 780 | -- | 773 | γ (C6-H10) (39) + γ (C5-H9) (20) + γ (C1-H7) (17) + γ (C2-H8) (10) | γ (C-H) |
| ν26 | 720 | 736 (43,1)0.75 | -- | 690 | -- | 712 | τ (C3-O11) (64) + ω (NO2) (24) + γ (C4-N13) (7) | τ (C-O) |
| ν27 | 683 | 698 (83,0)0.75 | -- | 697** | -- | -- | ω (NO2) (47) + τ (C3-O11) (20) + Φ1 (R) (17) + γ (C1-H7) (7) | ω (NO2) |
| ν28 | 667 | 682 (9,4)0.20 | 667 | 669** | 666 | -- | ν (C4-N13) (9) +α2 (R) (39) + α3 (R) (16) +ν (C5-C6) (8)+ν (C1-C2) (5) + δ (NO2) (12) | ν (C-N) |
| ν29 | 657 | 671 (16,0)0.75 | -- | -- | -- | -- | Φ1 (R) (53)+γ (C3-O11) (23)+γ (C4-N13) (11) | Φ (R) |
| ν30 | 559 | 571 (1,12)0.74 | 581 | 563* | 561 | -- | α2 (R) (25)+α3 (R) (10)+β (C4-N13) (22)+ ρ (NO2) (16)+ν (C4-C5) (9) + β (C3-O11) (8) | α (R) |
| ν31 | 542 | 554 (8,3)0.14 | 549 | 546* | -- | 554 | ρ (NO2) (24) + β (C3-O11) (20) + α2 (R) (12) + α3 (R) (11) + ν (C4-N13) (6) | ρ (NO2) |
| ν32 | 522 | 533 (8,0)0.75 | -- | 531 | -- | 536 | γ (C3-O11) (29) + Φ3 (R) (32) + Φ1 (R) (16) + γ (C6-H10) (9) + Φ2 (R) (6) | γ (C-O) |
| ν33 | 427 | 436 (2,4)0.56 | 427 | 426* | 424 | 437 | β (C3-O11) (34)+ρ (NO2) (33)+α3 (R) (11) +ν (C4-N13) (9) | β (C-O) |
| ν34 | 413 | 422 (1,0)0.75 | -- | -- | -- | 401 | Φ2 (R) (45)+ Φ3 (R) (15) + γ (C4-N13) (28) | Φ (R) |
| ν35 | 373 | 381 (6,1)0.20 | -- | 372* | -- | -- | α3 (R) (24) + α2 (R) (6)+β (C3-O11) (32) + ν (C4-N13) (19) + ρ (NO2) (7) | α (R) |
| ν36 | 285 | 291 (5,3)0.44 | 297 | 285* | 284 | -- | β (C4-N13) (73) + ρ (NO2) (9) | β (C-N) |
| ν37 | 240 | 245 (0,1)0.75 | -- | 251* | -- | -- | γ (C4-N13) (36) + Φ3 (R) (20) + Φ2 (R) (16) + Φ1 (R) (12) + γ (C2-H8) (9) | γ (C-N) |
| ν38 | 141 | 144 (0,1)0.75 | 159* | -- | -- | Φ3 (R) (44) + Φ1 (R) (4) + τ (C3-O11) (24) + γ (C4-N13) (20) | Φ (R) | |
| ν39 | 74 | 76 (1,0)0.75 | 67 | 85 | -- | -- | τ (C4-N13) (74) + τ (C3-O11) (17) | τ (C-N) |
Table 4: Computed and observed vibrational fundamentals, PEDs and vibrational modes assignments for lowest energy conformer C-1 of 2-NP
Phenyl ring modes (30): The four C-H stretching modes ν (C-H) are assigned to the frequencies 3034 (ν5), 3181(ν4), 3186(ν3) and 3205(ν2) cm-1 which correspond dominantly to the modes ν(C1-H7), ν(C6-H10), ν(C2-H8) and ν(C5-H9) respectively. The C-H stretching modes ν (CH) were assigned to the frequencies 3070, 3088, 3096 and 3117 cm-1 [41] and also to the frequencies 3208, 3229 and 3245 cm-1 [48]. The C-H stretching vibrations are pure and highly localized modes. There are 6 C-C stretching modes ν(R) due to the phenyl ring which are identified as the computed frequencies 1002 (ν19), 1051 (ν18), 1306 (ν12), 1420 (ν10), 1547 (ν7), 1586 (ν6) cm-1. These modes are strongly coupled with many other modes. These modes were assigned to the frequencies 1020, 1581 and 1620 cm-1 [41] and also to the frequencies 1369, 1551, 1584 and 1612 cm-1 [48]. The C-N and C-O stretching modes occur at frequencies 667 (ν28), 1442 (ν9) cm-1 corresponding to the modes ν(C4-N13) and ν(C3-O11) respectively. These modes are also coupled with many other modes. The C-O stretching mode in the literature was found to be corresponding to the frequency 1269 [41] and 1464 cm-1 [48].
There are three ring planar deformation modes which we assign as the frequencies 865(ν22), 559(ν30) and 373(ν35) cm-1. These modes are coupled with other modes as shown in the Table 4.The three ring nonplanar deformation modes are correlated to the frequencies 657(ν29), 413(ν34) and 141(ν38) cm-1 corresponding to modes 4 and 16(a,b) of the benzene molecule. These modes were found to occur at frequencies 152, 297 and 565 cm-1 [48].
The four C-H planar deformations β(C-H) and four C-H nonplanar deformations γ(C-H) are assigned at the frequencies 1106(ν17), 1177(ν15), 1260(ν13), 1131(ν16), 978(ν20), 849(ν23), 956(ν21) and 760(ν25) cm-1 corresponding to the modes β(C1-H7), β(C2-H8), β(C5-H9), β(C6-H10), γ(C1-H7), γ(C2-H8), γ(C5-H9) and γ(C6-H10) respectively. These modes are coupled with many other modes. The modes β(C-N), γ(C-N), β(C-O) and γ(C-O) correspond to the frequencies 285(ν36), 240(ν37), 427 (ν33) and 522(ν32) cm-1 respectively. These modes are strongly coupled modes. The modes β(C-N) and β(C-O) were assigned to the frequencies 298 and 432 cm-1 [41].
O-H group modes (3 modes): The OH stretching ν(O11-H12) mode corresponds to the frequency 3453(ν1) cm-1. The O-H stretching vibration is pure and highly localized mode. The O-H stretching mode was found to correspond to the frequency 3255 [41] and to the frequency 3308 cm-1 [48]. The torsion of the OH group - τ(C3-O11) occurs at frequency 720(ν26) cm-1 in our work and at the frequency 711 cm-1 [41] and is strongly coupled with other modes of vibrations. The C-O-H angle bending- α(C3-O11-H12) mode is found to correspond to the frequency 1349(ν11) cm-1 and also to the frequencies 1377 cm-1 [41] and 1266/1426 cm-1 [48], which is also strongly coupled with many modes.
NO2 group modes (6 modes): There are six modes of vibrations due to the NO2 group , namely, asymmetric NO2 stretching -νas(NO2), symmetric NO2 stretching-νs(NO2), NO2 rocking-ρ(NO2), NO2 wagging-ω(NO2), NO2 scissoring -δ(NO2) and NO2 torsion-τ(NO2) which correspond to the frequencies 1511(ν8), 1226(ν14), 542(ν31), 683(ν27), 819(ν24) and 74(ν39) respectively. The NO2 torsion-τ(NO2) is slightly coupled with τ(C3-O11) and the other five modes strongly coupled with various vibrational modes. The modes νas(NO2), νs(NO2), ω(NO2), δ(NO2) and τ(NO2) were found to correspond to the frequencies 1560, 1294, 741, 818 and 75 cm-1 [41] and also 1531, 1258, 702, 825 and 165 and also ρ(NO2) corresponds to the frequency 505 cm-1 [48].
Comparative study of vibrational modes for the three conformers: The computed vibrational fundamentals of the three conformers of 2-NP together with their respective differences have been collected in Supplementary material (Table S1). It could be seen that the modes τ(C-OH) and ν(O-H) of the OH group show very large frequency differences (in the range 350-400 cm-1). Also, the modes τ(C4-N13), β(C3-O11), ω(NO2) α(C3-O11-H12) and νas(NO2) show frequency differences of the order of a few tens of a wave number. Clearly, major contribution for this frequency difference is expected to come from H bonding between H12 and O15 atoms in the conformer C-1 which is absent in the conformers C-2 /C-3. The phenyl ring modes Φ3(R),α3(R), Φ2(R), γ(C-H) and ν(C-H) in the C-1 conformer have higher magnitudes than the corresponding modes in the conformers C-2 / C-3. However, the modes ω(NO2), β(C3-O11), ν(O11-H12), Φ1(R), ν(C3-O11), ν(R) and β(C2-H8) have higher frequencies in the conformers C-2 /C-3 than their corresponding modes in the most stableone.
The IR intensities and Raman activities for each of the three conformers are collected in Supplementary material (Table S2). It is noticeable that the IR intensities for the C-1 conformer are much higher than those of the C-2/C-3 conformers for the modes ν(O11-H12), ν(C3-O11), νs(NO2), β(C2-H8), β(C1-H7), ν(R) ω(NO2), ρ(NO2) and β(C4-N13) (S2).
The IR intensities for the modes α(C3-O11-H12), νas(N13-O14), τ(C3-O11), α1(R), ν(C2-H8), ν(C5-H9), ν(O11-H12), νs(NO2), α2(R), γ(C6-H10), β(C2-H8), β(C5-H9), δ(NO2) β(C3-O11), ν(C1-H7) and γ(C4-N13) for the conformers C-2/C-3 are much higher than the conformer C-1. One could see the major differences in the Raman activities for the modes νs(NO2), ν(C3-O11), α(C3-O11-H12), ν(C2-H8), ν(R) ν(C5-H9), as(NO2), ν(O11-H12), ν(C1-H7), δ(NO2), β(C1-H7), β(C6-H10) ν(C6-H10), and β(C4-N13). Such discrepancies could be due to the hydrogen bonding in the conformer C-1and the non-planar geometry of the C-2/C-3 conformers of 2-NP. The highest IR intensity and Raman activity for C-1 occur for the modes ν(O11-H12) and ν(C2-H8) respectively and those for C-2/C-3 for νas(NO2) and ν(C2-H8) respectively. From the above discussion it is clear that the intra-molecular H-bonding plays a crucial role in the molecular conformation.
HOMO–LUMO energy gap
The HOMO and LUMO studies are very important for quantum chemistry. These orbitals are also known by the name frontier orbitals, because they lie at the outermost boundaries of the electrons of the molecules. Both the HOMO and the LUMO are the main orbitals that take part in the chemical stability [49]. The kinetic stability of the molecule is measured in terms of energy gap DE [32,50] and the difference of the energies of the HOMO and LUMO is a measure of the excitability of the molecule, the smaller the energy, more easily it can be excited and vice versa. The lower HOMO and LUMO energy gap explains the eventual CT interaction taking place within the molecule, which is responsible for the bioactivity of the molecule. The larger the value of the energy gap the higher the kinetic stability and lower the chemical reactivity because it is energetically unfavorable to add electrons to a high lying LUMO, to remove electrons from a low lying HOMO and so to form the activated complex of any potential reaction [33]. The sketch of the atomic orbital compositions of the frontier MOs are shown in Figure 7. The green and red solid regions in Figure 7 represent the MOs with completely opposite phases. The present calculations predict that the energy gap (DE) of the 2-NP, i.e. the transition energy from HOMO to LUMO of the 2-NP is 0.148189 a.u. This electronic transition corresponds to the transition from the ground to the first excited state and is mainly described by an electron excitation from HOMO to LUMO.
Global reactivity descriptors
A molecule having high ionization potential (Vp) or electron affinity (VA) loses or admits electron hardly [51,52]. By Koopmans’ approximation [53,54], the ionization potential and electron affinity of any molecule can be calculated using the relations,
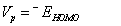

Koopmans` theorem for closed-shell molecules [54] results in the hardness of the molecule;
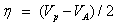
The chemical potential of the molecule;
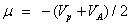
The softness of the molecule;
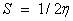
The electro negativity of the molecule;
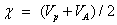
The electro-philicity index of the molecule;
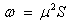
Using the above relations we find the electro molecular characteristics for 2-NP has been presented in Table 5.
| Reactivity Descriptor | Dipole Moment (μ) | Polarizability (α) | 1st order Hyperpolarizability (β) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Para. | Exact | Perturbation to α | |||||||||
| Para. | Value | Para. | Debye | (a.u.) | esu *10-24 | (a.u.) | esu *10-24 | Para. | a.u. | esu *10-32 | |
| Vp | 6.635 | (μx)FI | -3.951 | αxx | 123.434 | 18.268 | 74.308 | 10.998 | βxxx | 524.773 | 4534.563 |
| VA | 0.881 | (μy)FI | -0.611 | αxy | -0.198 | -0.029 | -1.208 | -0.179 | βxxy | -125.223 | -581.160 |
| η | 2.877 | (μz)FI | -0.001 | αyy | 105.178 | 15.566 | 95.758 | 14.172 | βxyy | -102.311 | -884.069 |
| μ | - 3.758 | (μ)FI | 3.998 | αxz | -0.005 | -0.001 | -0.002 | -0.0003 | βyyy | -95.389 | -824.256 |
| S | 0.174 | (μx)esp | -3.964 | αyz | 0.012 | 0.002 | 0.023 | 0.003 | βxxz | -0.080 | -0.691 |
| χ | 3.758 | (μy)esp | -0.603 | αzz | 47.285 | 6.998 | 23.282 | 3.446 | βxyz | -0.023 | -0.199 |
| ω | 2.457 | (μz)esp | -0.003 | α0 | 91.966 | 13.612 | 64.449 | 9.538 | βyyz | -0.014 | -0.121 |
| Eg | 4.03 | (μ)esp | 4.010 | Δα | 9483.787 | 1403.600 | 8325.284 | 1232.142 | βxzz | -75.942 | -656.215 |
| βyzz | -27.380 | -236.590 | |||||||||
| βzzz | -0.013 | -0.112 | |||||||||
| βtotal | 426.118 | 3681.229 | |||||||||
Table 5: Molecular reactivity and NLO parameters of C-1 conformer of 2-NP.
NLO characteristics: Static polarizability and first order hyperpolarizability
Quantum chemical computational theory has been shown to be essential in the description of the relationship between the electronic structure of the systems and its NLO response [55]. The NLO activities provide the key functions for frequency shifting, optical switching, optical modulation and optical logic to develop the technologies for the communication, signal processing and optical interconnections [56]. The electric dipole moment (μ), the polarizability (α) and the hyper polarizability (β) of the 2-NP molecule have been calculated by finite field method using DFT-B3LYP method employing 6-311++G(d,p) basis set for the isolated molecule, the origin of the Cartesian coordinate system (x, y, z) = (0, 0, 0) was chosen at own centre of mass of 2-NP. In the presence of an external electric field, the energy of a system is a function of the field and the first hyperpolarizability is a third rank tensor that can be described by a 3x3x3 matrix. The 27 components of the 3D matrix can be reduced to 10 components using the Klein man symmetry [57]. The matrix can be given in the lower tetrahedral format. Clearly, the lower part of the 3x3x3 matrices is a tetrahedral. The components of β are defined as the coefficients in the Taylor series expansion of the energy in the external electric field. If the external field is weak and homogeneous, this expansion is as given below,
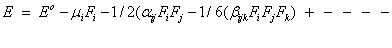
Here, Eo is the energy of the unperturbed molecules, Fi is the field at the origin, μi, αij and βijk are the components of dipole moment, polarizability and first hyperpolarizability, respectively.
The total static dipole moment μ, the mean polarizability α0, the anisotropy of the polarizability Δα and the mean first hyperpolarizability β0, using the x, y and z components are defined as;
Dipole moment;
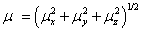
Static polarizability;
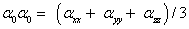
The total polarizability;
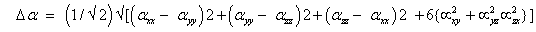
First order hyperpolarizability;
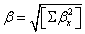
Where
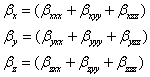
The static polarizability α0 (91.966 au) and total polarizability Δα (9483.787 au) of the 2-NP together with all its components and perturbation to all its components, first order hyperpolarizability (β = 426.118 au) and its components and the total as well as components of the dipole moment have been tabulated in the Table 5.
Electrostatic potential
The electrostatic potential (ESP) is the tool which is used to study the intermolecular association and molecular properties of small molecules, actions of drug molecules and their analogues, the biological function of haemoglobin and enzyme catalysis [33,58-61]. ESP is widely used as the reactivity map displaying most probable regions for the electrophilic attack of charged point-like reagents on organic molecules [62]. The values and spatial distribution of ESP are in fact responsible for the chemical behaviour of an agent in a chemical reaction. They strongly influence the binding of a substrate to its active site. ESP is typically visualized through mapping its values onto the molecular ED. The different values of the electrostatic potential at the surface are represented by different colors; the red represents regions of the most negative electrostatic potential, the blue represents regions of the most positive electrostatic potential and the green represents regions of zero potential. Potential increases in the order red, orange, yellow, green and blue. While the negative electrostatic potential corresponds to an attraction of the proton by the concentrated ED in the molecule (and is colored in shades of red), the positive electrostatic potential corresponds to the repulsion of the proton by atomic nuclei in regions where a low ED exists and the nuclear charge is incompletely shielded (and is colored in shades of blue). The total density plot and its array of the 2-NP are shown in the Figure 8. The molecular ESP values, corresponding to Merge-Singh-Koll man scheme [47], of the 2-NP molecule have been arranged in the Table 3. Also, the diagrammatic demonstration of the MESP via map and its contour has been shown in Figure 9. These Figs provide a visual representation of the chemically active sites and comparative reactivity of atoms. The ESP plots and the value arranged in the Table 3 predict that there are no regions of positive and zero potential present in the molecule. Also, the Figure 9 and the data in the Table 3 predict that the sites associated with the functional groups, namely, OH and NO2 groups are most reactive sites for the neucleophilic reactions.
Thermo molecular characteristics
The studies of some thermo molecular characteristics, namely, zero point vibrational energy, enthalpy, Gibb’s free energy, internal energy, entropy, heat capacity, thermal energy and the partition functions etc. have been found to play crucial role in the material characterization. We have presented some thermal parameters in Table 6. It can be noticed that all of the analysed thermodynamic parameters are increasing with the temperature but G is found to decrease with T [Figure 10(a)-10(h)] while the zero point vibrational energy remains constant (67.226 Kcal/ mol) at all the temperature because it is a characteristic property of the molecule. All the fitting parameters and other essential statistical data have been demonstrated together with the fitted graphs of these parameters. All of the characteristic thermal properties of crystalline 2- NP solid have been found to be in agreement with the explanation of Dulong-Pettit law as well as of Einstein’s thermo dynamical theory of crystalline solids. The fitting equations of the thermal parameters of 2-NP are as given below;
| T (K) | G Kcal/mol | H Kcal/mol | Q Kcal/mol | C cal/mol-K | S cal/mol-K | U Kcal/mol | ZPE Kcal/mol | LnQV=0 | LnQBot |
|---|---|---|---|---|---|---|---|---|---|
| 100 | 61.7744 | 68.2344 | 68.037 | 11.236 | 64.604 | 67.6919 | 67.226 | 27.427241 | -310.866945 |
| 200 | 54.7113 | 69.9739 | 69.578 | 19.973 | 76.312 | 69.4314 | 67.226 | 31.484367 | -137.662726 |
| 298.15 | 46.7007 | 72.6006 | 72.010 | 29.552 | 86.870 | 72.0581 | 67.226 | 34.641248 | -78.823178 |
| 300 | 46.5394 | 72.6589 | 72.064 | 29.728 | 87.066 | 72.1164 | 67.226 | 34.697505 | -78.067224 |
| 400 | 37.3109 | 76.2864 | 75.493 | 38.613 | 97.440 | 75.7439 | 67.226 | 37.633424 | -46.940123 |
| 500 | 27.0689 | 80.7254 | 79.734 | 45.928 | 107.316 | 80.1829 | 67.226 | 40.415236 | -27.243602 |
| 600 | 15.8687 | 85.8181 | 84.628 | 51.726 | 116.585 | 85.2756 | 67.226 | 43.073074 | -13.309290 |
| 700 | 3.7721 | 91.4280 | 90.039 | 56.315 | 125.223 | 90.8855 | 67.226 | 45.615146 | -2.712595 |
| 800 | -9.1554 | 97.4488 | 95.861 | 60.001 | 133.258 | 96.9063 | 67.226 | 48.045839 | 5.759065 |
| 900 | -22.8595 | 103.8028 | 102.017 | 63.013 | 140.739 | 103.2603 | 67.226 |
Table 6: Some crucial molecular thermodynamic parameters of C-1 conformer of 2-NP.
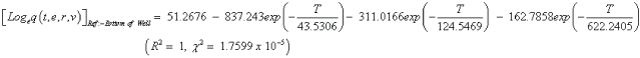
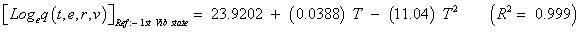
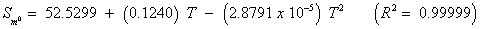
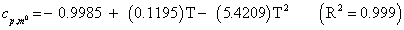
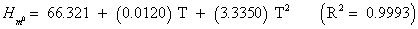
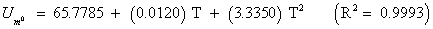
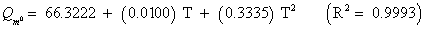
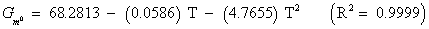
All the thermo molecular data provide the crucial and helpful information for the further study on the 2-NP. They can be applied to compute the other thermodynamic characteristics according to relationships of thermo dynamical parameters and estimate directions of chemical reactions according to the second law of thermodynamics in thermo chemical fields. It should be noticeable that all calculations of thermo dynamical parameters have been done in gas phase and they could not be used in solution phase.
NMR characterization: Magnetic susceptibility, shielding and current density tensors
The NMR analysis plays an essential part in material characterization in presence of magnetic fields. This type investigation provides chemical shifts and magnetic shielding tensors to each atomic site of the molecule as well as magnetic susceptibility and the current density tensor for the material being investigated. We have applied Continuous Set Gauge of Transformation (CSGT) method for NMR investigation of the 2-NP molecule. The magnetic susceptibility tensor of 2-NP has been computed as
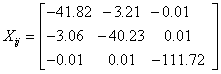
Having the Eigen values λ1 = -111.7209, λ2 = -44.2576 and λ3 = -37.7896 and the value of magnetic susceptibility χ is found to be -64.5893 cgs-ppm, the negative sign of χ shows the diamagnetic nature of the 2-NP molecule.
Also, the magnetic shielding tensors together with their corresponding Eigen values at different atomic sites computed are depicted as below;
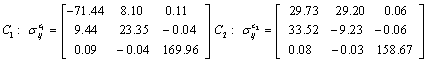
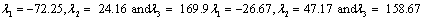
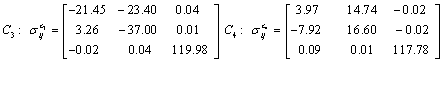
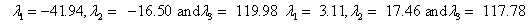
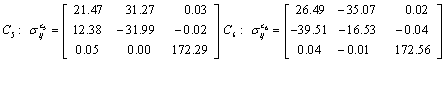
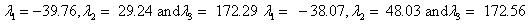
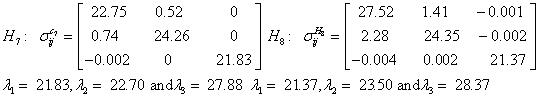
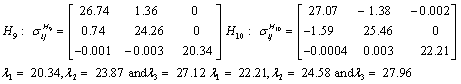
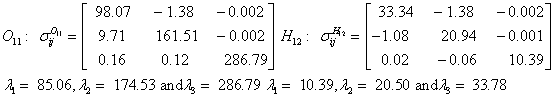
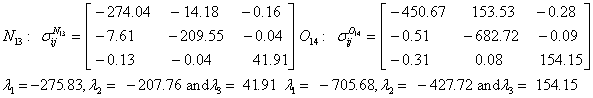
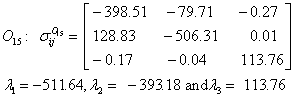
The magnetic shielding at the atomic sites, namely, C1, C2, C3, C4, C5, C6, H7, H8, H9, H10, O11, H12, N13, O14 and O15 have been computed 40.625, 59.723, 20.510, 46.115, 53.924, 60.840, 24.138, 24.414, 23.778, 20.340, 182.124, 21.558, -147.229, -326.418 and -263.685 ppm. respectively. It is noticeable that the shielding at every sites associated to NO2 group is negative and attaining higher values [Figure 11(a, b)]. From the Figure 11 it is obvious that the effect of the magnetic field is least nearby the NO2 group of 2-NP molecule.
The current density tensor (J) for the 2-NP have been computed and depicted in matrix form as;
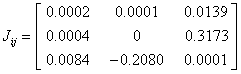
The two Eigen values of the current density tensor have been found imaginary while one Eigen value of J is λ=0.0002 for 2-NP molecule. The value of the J (~ 1.231x10-5 a.u.) has been found to be negligibly small, which reveals that the electrical conductivity of 2-NP molecule is negligibly small. The mapping and corresponding contour of J for the title molecule have been demonstrated diagrammatically (Figure 12). Figure 12 also represents that the current density is extremely weak for the 2-NP molecule.
For the first time; complete material characterization, complete vibrational mode assignment, conformational analysis, HOMO – LUMO analysis, complete data analysis on thermo-dynamical parameters, data analysis on reactivity parameters and on NMR parameters, potential energy distribution and investigations of APT, Mulliken atomic charges and ESP derived charge of 2-NP has been carried out. The 2-NP molecule has been expected to possess three conformations out of which lowest energy conformer is planar possessing Cs symmetry while other two are non-planar possessing C1 symmetry. Conformer C-1 is planar, in which NO2 group is in the plane of phenyl ring while in conformers C-2 and C-3 the plane of NO2 group makes the angle -33.70 and 33.70 respectively. The Nitrogen atom of NO2 group attains highest APT charge while carbon atom directly attached to OH group bears highest Mulliken charge. For lowest energy conformer α (C4-C3-O11) is largest (124.60) and α(C3-O11-H12) is smallest (107.30) respectively. For the modes τ(C3-O11) and ν(O11-H12) are found to have very large frequency differences 394 and -352 cm-1 respectively among the conformers C-1 and C-2/C-2. ν(O11-H12) is of largest IR intensity and ν(C2-H8) is found to be largest Raman activity mode. All the modes of vibrations are precisely assigned to the corresponding appropriate frequencies and also the experimental work has been compared with the computational work as well as the work already been carried out, which found to be in agreement with our work. The HOMO–LUMO transition clearly explicates CT interaction involving donor and acceptor groups. The ESP plots and corresponding values show that there are neucleophilic most reactive regions are found nearby OH and NO2 groups while no regions of positive and zero potential present in the molecule. The HOMO – LUMO energy gap is found to be ΔE = 0.148189 a.u. In conformer C-1 intramolecular hydrogen bonding O15......H12 is expected in 2-NP molecule. NMR investigations as well as HOMO- LUMO theory reveal that the conductivity of the title molecule is extremely low and the molecule is diamagnetic in nature.