Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2014) Volume 4, Issue 2
A large scale nationwide radon survey was conducted in Greek dwellings between 1994 and 2000. Twelve hundred passive CR-39 detectors were distributed and collected along with 963 filled in questionnaires. These were rechecked during 2012-13 to evaluate factors that potentially affect indoor radon concentrations, namely the factors (i) area (environment), (ii) building level-floor, (iii) ground type, (iv) basement, (v) building type, (vi) construction year, (vii) building walls contact, (viii) wall materials and (ix) floor materials. The questionnaires were prepared by the research team according to international standards. One-way and multivariate statistical methods were applied for the analysis, in specific (I) Linear Regression Analysis, (II) One way or multiway ANOVA, (III) General MANOVA, (IV) Stepwise Regression Analysis and (V) Principal Components Analysis. The results revealed that approximately 0.1% of the dwellings exhibited outlier radon concentrations. Noteworthy statistical correlations were detected between the measured mean annual indoor radon concentration levels and the factors (ii) (building level-floor) and (viii) (wall materials). Weak evidence was provided for the corresponding correlation with the factors (v) (building type) and (vii) (building walls contact). Minor was the association with the factors (iv) (construction year) and (ix) (floor materials). Significant differences were detected in the results of the applied statistical methods.
<Natural environmental radiation depends on local geology and hence, variations are addressed in human radiation exposure due to cosmic and terrestrial radiation [1]. 238U and 232Th are two natural parent isotopes which are present in soil and contribute significantly to natural terrestrial radioactivity. Radon (222Rn) is a radioactive noble gas and originates from 238U. 220Rn originates from 232Th and 219Rn from 235U. 222Rn, 220Rn, 219Rn are the primary sources of radon in soil, with 222Rn being dominant in rocks, soil, building materials, underground and surface waters [2] and set to be the most hazardous radionuclide. Radon (222Rn) and its short-lived progeny (218Po, 214Po, 214Bi, 214Pb) are attached in dust and in water droplets creating radioactive aerosols, that inhaled via breathing and enter human lungs. Radon enters buildings through gaps around pipes or cables and through cracks in floors [3]. Primary studies have shown that radon is the second most dangerous cause of lung cancer after smoking. This happens when alpha particles emitted from radon progeny damage pulmonary epithelium. Many studies have been made for the measurement of indoor radon concentrations in several countries [4-9]. Over the years, in Greece, indoor radon concentrations measurements, to our knowledge, are as follows: several small–scale [10-12], two middle – scale [3,13] and one large-scale [14].
Under the National Strategic Reference Framework (NSRF) “Thales” project of the Technological Education Institute of Piraeus and extending the aforementioned large scale radon survey, this paper addresses the grade of severity with which factors influence indoor radon concentration levels. Similar studies in other countries have shown that indoor radon concentrations are higher at lower floor levels [15-17]. Moreover, recent studies indicate that radon emanation from building materials contributes significantly in indoor radon concentration in dwellings [18-20]. Current work provides alternative approximations for studying the relative importance of various radon-affecting factors. Through a manifold manner, associations are quantified between several factors such as the “basement existence” and “ground type (sloppy, over-grounded)” with radon concentrations.
A thorough investigation was performed on whether nine factors: i) area (environment), ii) building level-floor, iii) ground type, iv) basement, v) building type, vi) construction year, vii) building walls contact, viii) wall materials, ix) floor materials, may affect indoor radon concentration independently or jointly. These factors have been recorded on 963 filled questionnaires of the greater large-scale survey in Greece [14]. The following statistical methods were applied on the questionnaire data: i) Linear Regression Analysis; ii) One way or multiway ANOVA; iii) General MANOVA; iv)Stepwise Regression Analysis; and v) Principal Components Analysis; It is noted that radon data from reference [14] were dispersed across Greece.
Linear regression analysis
In linear regression analysis, a straight line is fitted through a set of points-observations in such a way that the sum of squared residuals is minimal [21]. In multiple linear regression the dependent variable can be written in terms of a linear combination of the independent variables. The regression equation describes the correlation of the mean value of a variable- y with specific values of x-variables used to predict y.
If (x1, y1), (x2, y2),…, (xn, yn) are realisations of random variable pairs (x1, y1), (x2, y1),…, (xn, yn), then the linear regression equation expresses the mean of Y as a straight-line function of X which can be represented as
E(Yi) = β0 + β1 . Xi (2.1.1)
or E(Yi) = β0 + βi1 Xi + βi1 Xi + … + βip . Xp for p independent-predictor variables.
E(Yi) states the mean expected value and i points the population. The estimated/fitted model is then:
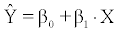 (2.1.2)
(2.1.2)
From (2.1.2), the estimated/fitted values for each of the n observations are
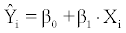 (2.1.3)
(2.1.3)
Where i = 1,…,n is the consecutive number of the population. From (2.1.2) and (2.1.3) the, so called, observed error or fitted residual is calculated as:
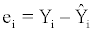 (2.1.4)
(2.1.4)
Equation (2.1.4) calculates the estimated error of the i-th observation in the sample. From (2.1.4) the sum of squared observed errors (SSE) equals
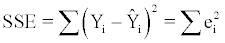 (2.1.5)
(2.1.5)
for all observations in a sample of size n. The mean square error (MSE) equals then
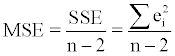 (2.1.6)
(2.1.6)
(“n-2” should be substituted by “n-p-1” when there are p predictorindependent variables) and this is the sample variance of error. The residual standard error is then calculated as
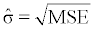 (2.1.7)
(2.1.7)
and σ2 should be the constant error variance, otherwise the confidence intervals will be misleading.
As
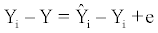 (2.1.8)
(2.1.8)
the total sum of squares (SST) equals
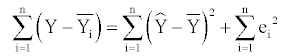 (2.1.9)
(2.1.9)
with 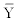 set to be the mean of all observed Y values.
set to be the mean of all observed Y values.
The coefficient of determination
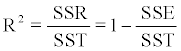 (2.1.10)
(2.1.10)
represents the proportion of variation in Y that is explained by X. Parameters β0, β1, ..., βp (regression coefficients), σ2 (variance) and R2 (coefficient of determination) need to be estimated in order to examine if the linear regression model applies to this group of data. However, even if R2 value is close to zero, this does not mean that X and Y have linear association and polynomial terms should not be included to improve the fitting.
One Way or multiway ANOVA:
Analysis of variance (ANOVA) is considered as the generalization of a t-test to more than two statistical groups. ANOVA is divided in two categories: i) One way, where a single factor exists and ii) two way or multiway, where two or more factors exist. ANOVA is used for distributional assumptions about a set of effects in a model, with ability to extrapolate the inferences to a wider population, improve accounting for system uncertainty and the efficiency of estimation. ANOVA has been implemented as the basic method for the statistical analysis of radon concentrations in many studies [9,22-24]. For the analysis of factors affecting indoor radon concentrations, initially each factor was analysed independently, according to Table 1. In such a way a first assumption for the weightiness of the effect of each factor is possible. In the next step, factors affection is no longer estimated independently; instead, factors influence each other and therefore are dependent. The aforementioned method is called random-effects assumption of the analysis of variance. ANOVA can be implemented only in sampling distributions similar to those of Gauss and, due to this, it was applied in the log distributions of radon measurements.
| Source of variation | SS | df | MS | F-value |
|---|---|---|---|---|
| Regression | 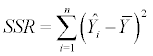 |
P | 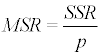 |
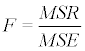 |
| Error | 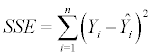 |
n− p− 1 | 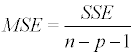 |
|
| Total | 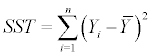 |
n− 1 | 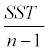 |
Table 1: The ANOVA table as applied in this study.
General MANOVA
Multivariate (multiple dependent variables) analysis of variance (MANOVA) is defined as a partition of the sum of squares and the sum of the cross products (SSCP) matrix
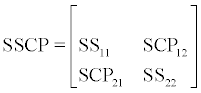 (2.1.2.1)
(2.1.2.1)
into independent Wishart matrices [25]. MANOVA is applied instead of a series of one-at-a-time ANOVAs. In several situations, the power of MANOVA is inferior to ANOVA of one variable at a time, however, MANOVA takes into account the intercorrelations among the dependent variables, according to Table 2. Hence, MANOVA is considered more efficient over ANOVA for multivariate data [25].
| Source of variation | SSCP | Df |
|---|---|---|
| Regression | 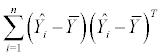 |
p −1 |
| Error | 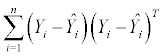 |
n − p |
| Total | 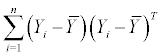 |
n −1 |
Table 2: The MANOVA table as applied in this study.
Issues in Multiple Regression
The difficulty with model selection emerges from the fact that for p predictors, there are 2p different candidate models. With so many possible interactions it can be difficult to find a good model. Model selection methods try to simplify this task. A true model may only depend on a subset of X1, ..., XP . In other words, in model
Y = β0 + β1X1 + ... + βpXp + ε (2.1.3.1)
some of the coefficients are zeros. The result will be the disclosure of those predictors with nonzero coefficients, i.e. the “best subset” of all predictors.
R2 can be used for models with the same number of parameters/ coefficients, otherwise 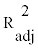 should be used. The best model has the biggest
should be used. The best model has the biggest 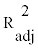 value.
value.
Selecting p predictors, the Mallows’ Cp criterion should be small with a value near to p.
Stepwise Regression Analysis
Stepwise methods are used in several areas of applied statistics. A statistical model can be constructed in two ways, namely (i) forward selection and (ii) backward elimination. Forward selection means that a specific number of variables exist in the beginning and gradually variables are added, one at a time, in optimal way in order to analyse the effect of each variable. Alternatively, with backward elimination, all potential variables exist in the beginning and non-effective variables are subtracted, one at a time, until a desirable stopping point is reached.
Stepwise regression forms a hybrid model between forward selection and backward elimination. More precisely, steps have a forward direction with variable addition, however if a variable is characterized as non-significant, it is removed as in backward elimination. In literature stepwise regression has been used for the prediction of mean indoor radon concentrations [26], in the construction of radon maps based in indoor radon measurements and soil geochemical parameters [27] and in risk analysis of factors affecting lung cancer [28].
Principal Components Analysis
Principal components analysis (PCA) is used for the reduction of the number of possible clusters. PCA offers the ability for the identification of patterns within large sets of data [29]. Its significance rely in the occurrence of a relative redundancy in the variables, due to their correlation in the measurement of the same construct. During the analysis of the principal components, eigenvalues represent the relative participation of each factor in presenting the general variability of the sampled data [30]. PCA has several implementations in factors investigation of water quality, in drug development, in cancer detection and in health care [30-33]. PCA has been also used for the investigation of the dependence among variables and for the prediction of relationships among variables.
Figure 1 presents characteristic residual plots calculated from the measured average concentrations of radon (C) and their logarithms (log (C)). It is noted that the C values of Figure 1 correspond to time-integration over a year, constitute representative sample for Greece, were derived in accordance to international standards and delineate the radon profile of Greece [26]. In this consensus, Figure 1 is of significance since it may show actual tendencies regarding the randomness or predictability of the employed concentration sample. Indeed, completely randomised responses to normal-distribution either of C or log (C), would exhibit no deterministic normal-distribution’s residuals and, hence, be completely described by stochastic processes. The normal probability plots of Figures 1a and 1b indicate, however, that the logarithms of the measured concentration followed normal distribution up to the 95% of log (C) values, namely indicated that C values followed log-normal distribution. This is also evident from the shapes of the frequency distributions of the residuals. The frequency distribution of Figure 1a was clearly log-normal, while simultaneously that of Figure 1b, clearly normal. This is also of significance because all international large-scale radon surveys reported log-normal behaviour of indoor radon concentrations. The reason is rational, namely that is why the C values did not follow normal distribution, as it is shown in the corresponding normal probability plot of Figure 1a. Under another view, the residual plots of log (C) versus values, fitted to normaldistribution, showed random patterns for the fitted residual values of log (C) above 1.6. It is noted that a residual of 1.6 in log (C) is consistent with an uncertainty of σC = 39.8 Bq.m-3 in the predicted C values. This, according to the recording capabilities of the employed dosemeters [34], accompanies high C values, namely C values above the EU action limit of 200 Bq.m-3. Moreover, the majority of predicted residuals were below 1.2. This is very significant because this residual range is consistent with concentrations usually addressed, namely between 10 – 120 Bq.m-3. Other factors may affect concentrations in this range, and, surely the potential factors could not be continuous under the normal distribution. Indeed, the Versus Fits diagram of Figure 1a shows characteristic predictability, different from the normal distribution for the residual C range below 75 Bq.m-3. On the other hand, the residuals versus observation order, did not showed tendencies for concentrations up 160 Bq.m-3, either in the concentration order (Figure.1a), or, the order of the concentration’s logarithm.
Figure 1: Residual plots of (a) radon concentration and (b) logarithm of radon concentration.
All measurements are shown. Each plot contains (I) percentage of residuals versus residual, (II) frequency distribution of the residuals, (III) residual versus fitted values according to C for (a) and log (C) for (b) and (IV) residual versus observation order.
Table 3 presents the analysed factors, factor levels and level values with their corresponding description. Data of Table 3 were formulated in accordance to the contents of the 963 questionnaires which were filled during the radon survey of Greece. It is noted that these questionnaires were developed in agreement to other national surveys. All factors exhibited 3-4 levels. This is worth to notice, because a multilevel collection of factors can distract results, especially for limited number of measurements. Factor (Level- L) was 5-level marking the usual situation of apartment dwellings in big cities of Greece. Nevertheless, this 5-level factor is easily convertible to a lower-level one. Factor (Floor’s material- F) was free to fill, so a 6 level collection was finally achieved.
| Factor | Type | Levels | Values | Description |
|---|---|---|---|---|
| Area- A | fixed | 3 | 1; 2; 3 | Agricultural, Suburban, Urban |
| Level- L | fixed | 5 | 0; 1; 2; 3; 4 | Ground Floor,1st, 2nd, 3rd, >4th floor |
| Ground Type- G | fixed | 3 | 0; 1; 2 | Normal, Sloppy, Over-grounded |
| Basement- Bas | fixed | 3 | 0; 1; 2 | No bas, Full coverage, Semi coverage |
| Building Type- BTy | fixed | 3 | 0; 1; 2 | Detached, Semi-Det, Apartment |
| Year- Y | fixed | 4 | 0; 1; 2; 3 | <1900, 1900-50, 1950-80, >1980 |
| Wall Contact- Con | fixed | 4 | 0; 1; 2; 3 | no, 1, 2, 3 |
| Wall's material- W | fixed | 4 | 0; 1; 2; 3 | brick/concrete, stone, combin, other |
| Floor's material- F | fixed | 6 | 0; 1; 2; 3; 4; 5 | concr/tile, concr/mos, concr/marble, concr/wood, concr, rock |
Table 3: Descriptions of used factors (qualitative)
It is well identified that Gauss distribution offers a rigid and justified pathway for statistical analysis. Since concentrations’ logarithms followed the distribution of Gauss, log (C) was considered favourable. Hereafter, analysis was conducted only on log (C). Table 4 presents the unusual observations in log (C) values accounting that these followed normal distribution, viz. were treated according to the distribution of Gauss. Leverage points were considered to be those observations corresponding to extreme or outlying values of log (C) in a manner that any lack of neighbouring observations implied that the fitted Gaussian regression model passed close to the particular observation. In specific, leverage points were calculated by moving all points one-by-one up or down and calculating the proportionally constant (leverage) of the change of the corresponding Gaussian fitted value. Outliers were calculated as the observations that presented residuals above 1.5 times the interquartile range. According to Table 4, eight outlier (R) and two leverage (X) residual points were identified. In any case, unusual log (C) values were approximately 0.1% of the total concentration sample size. Therefore, they constituted a negligible part of measurements. Importantly, however, the latter finding indicates that only a small portion (<0.1%) of Greek dwellings presented unusual concentrations. Considering that high unusual concentration extremes may associate with high human radiation burden, this fact implies that indoor radon in Greece may not lie in the international extremes. Emphasis should be stressed also on the fact that outlier data affect any type of fit and should be removed prior to regression analysis, whereas, leverage point may or may not affect. For this reason, all outlier and leverage points were finally removed from the dataset.
| O | log(C) | Fit | SE-F | Residual | SR |
|---|---|---|---|---|---|
| 2 | 2.43459 | 1.52274 | 0.13233 | 0.91185 | 2.95 R |
| 5 | 1.15278 | 1.15278 | 0.33620 | -0.00000 | * X |
| 26 | 2.54306 | 1.54974 | 0.15743 | 0.99332 | 3.34 R |
| 40 | 2.46026 | 1.70575 | 0.10492 | 0.75451 | 2.36 R |
| 45 | 1.01375 | 1.68231 | 0.14050 | -0.66856 | -2.19 R |
| 56 | 1.02208 | 1.02208 | 0.33620 | 0.00000 | * X |
| 87 | 2.35829 | 1.43778 | 0.08382 | 0.92051 | 2.83 R |
| 97 | 0.72033 | 1.43709 | 0.13810 | -0.71676 | -2.34 R |
| 108 | 2.39661 | 1.52606 | 0.07437 | 0.87055 | 2.66 R |
| 126 | 0.80896 | 1.54284 | 0.09904 | -0.73388 | -2.28 R |
Table 4: Unusual Observations for log (C). O denotes the number of observation, SE-F the standard error of the fit and SR the standardised residual. R denotes observations with large standardized residual (outliers). X denotes observations that gave large leverage.
Table 5 presents the combinations to define the best subsets from the nine factors of Table 3 for the regression of log (C). As in Table 4, regression was linear to the factors employed in each entry of Table 5. Mallow’s Cp (MCP) was calculated for any subset of k,k ≤ p of explanatory variables, as  , where SSEp was the residual sum of squares for the subset model containing p explanatory variables counting the intercept (i.e., the number of parameters in the subset model), MSE the mean square error and n is the sample size. It should be emphasised that, acceptable models in the sense of minimizing the total bias of predicted values, are those models for which Cp approaches the value p, i.e., those subset models that fall near the line Cp = p in a plot of Cp against p for the collection of all subset models under consideration. Under this view, only the combination of all factors except factor G (Ground Type, Table 3) constitutes an acceptable subset that could minimise total bias.
, where SSEp was the residual sum of squares for the subset model containing p explanatory variables counting the intercept (i.e., the number of parameters in the subset model), MSE the mean square error and n is the sample size. It should be emphasised that, acceptable models in the sense of minimizing the total bias of predicted values, are those models for which Cp approaches the value p, i.e., those subset models that fall near the line Cp = p in a plot of Cp against p for the collection of all subset models under consideration. Under this view, only the combination of all factors except factor G (Ground Type, Table 3) constitutes an acceptable subset that could minimise total bias.
| V | R2 | 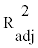 |
MCP | SE | A | L | G | Bas | B Ty | Y | Con | W | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.1 | 1.5 | -0.8 | 0.33511 | X | ||||||||
| 1 | 1.1 | 0.5 | 0.8 | 0.33677 | X | ||||||||
| 2 | 2.9 | 1.7 | -0.2 | 0.33465 | X | X | |||||||
| 2 | 2.8 | 1.6 | -0.0 | 0.33481 | X | X | |||||||
| 3 | 3.7 | 1.9 | 0.5 | 0.33434 | X | X | X | ||||||
| 3 | 3.6 | 1.8 | 0.6 | 0.33446 | X | X | X | ||||||
| 4 | 4.6 | 2.2 | 1.1 | 0.33384 | X | X | X | X | |||||
| 4 | 4.0 | 1.6 | 2.0 | 0.33483 | X | X | X | X | |||||
| 5 | 5.0 | 2.0 | 2.4 | 0.33419 | X | X | X | X | X | ||||
| 5 | 4.8 | 1.8 | 2.8 | 0.33460 | X | X | X | X | X | ||||
| 6 | 5.2 | 1.6 | 4.1 | 0.33487 | X | X | X | X | X | X | |||
| 6 | 5.1 | 1.5 | 4.3 | 0.33511 | X | X | X | X | X | X | |||
| 7 | 5.2 | 1.0 | 6.0 | 0.33586 | X | X | X | X | X | X | X | ||
| 7 | 5.2 | 1.0 | 6.1 | 0.33591 | X | X | X | X | X | X | X | ||
| 8 | 5.3 | 0.4 | 8.0 | 0.33691 | X | X | X | X | X | X | X | X | |
| 8 | 5.2 | 0.4 | 8.0 | 0.33694 | X | X | X | X | X | X | X | X | |
| 9 | 5.3 | 0.0 | 10.0 | 0.3800 | X | X | X | X | X | X | X | X | X |
Table 5: Best subsets regression: log (C) versus all factors. R2, adjusted 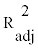 , Mallow’s Cp (MCP) and standard error (SE) in each subset is presented. V denotes the number of factors included within each model.
, Mallow’s Cp (MCP) and standard error (SE) in each subset is presented. V denotes the number of factors included within each model.
Additionally to the analysis presented so-far, one-way ANOVA was applied to single-factor data from the whole data set. Analysing factor Level-L in its full depth, a f value of 2.551 was calculated, whereas the critical f value at the 95% confidence interval - CI is 2.03. These values imply that with p= 0.014, results from the various different levels collected did not differ significantly. However when the full dwellinglevel data were reorganised in 3-levels (ground floor, first floor and upper floors) f value was found equal to 7.156 while the corresponding critical value at the 95% CI is 3.01 with corresponding value p = 0.000877. This finding is significant, since it implies that with p<0.001, lower level dwellings present higher indoor radon concentrations. Further evidence was provided by reorganising dwelling-level data in 2 levels, namely ground floor and higher floor dwellings. Applying t-test to the average concentrations it was calculated that at p<0.001, ground floor dwellings presented higher radon concentrations. Analysing factor “Wall Contact-Con” with one-way ANOVA, an f value of 0.893 was calculated, whereas the critical f value at the 95% CI is 2.624. Namely, at p<0.001different Wall Contact - factor level dwellings did not present differences. Similar was the outcomes of the one-way ANOVA for factor “Floor’s material-F”. Non significant variations were addressed, since calculated f value was 1.298 and the critical value at 95% CI, 2.119. On the contrary, the one-way analysis of factor “Wall’s material-W”, provided an f value of 4.314 with a critical value at 95% CI of 2.624 and an associated p value of 0.0051. The latter finding was associated with a tendency of higher concentrations of rock dwelling.
Table 6 presents the results of the general MANOVA method. These results support further findings of the one-way ANOVA. Nonsignificant statistical interactions between any combinations of factors were detected by General MANOVA
| Factor | p value |
|---|---|
| Area- A | 0.131 |
| Building Type- BTy | 0.162 |
| Floor's material- F | 0.185 |
| Level- L | 0.208 |
Table 6: General MANOVA for log(C). Cut-off Limit for significance level < 30%
Table 7 presents the results of stepwise regression of log (C) versus all factors. Through stepwise regression, a linear model was sought containing only those variables which were significant in modelling log (C). The qualitative factor levels of Table 3 were employed in their original values so as to be transformed to quantitative variables. It should be stressed, that stepwise regression is particularly useful when there are many possible explanatory (independent) variables. Some of these variables may be highly correlated with each other and therefore may explain the same variation in the response and not be independently predictive. Some may also not influence the response in any meaningful way. Employing high alpha values for the error probability in Table 7, only three factors were finally selected, and these after the third step. It is noted that probability values, p , and alpha values, a , are related as p = 1 - a and, thus, the results of Table 7 correspond to the 50% significance level, either for accepting entering of a certain factor, or, for its removal. According to Table 7 the main factors found to influence indoor radon concentrations were “Wall’s material- W”, “Level- L” and “Wall Contact- Con”. In specific, factor contact exhibited p-value of 0.162, factor level, 0.131 and factor wall 0.276 (error probability 50%). This implies that at a significance level <17% level and contact affect indoor radon concentration, while at the 30% significance level, all three factors affect. These results, however, provide vague evidence on the null hypothesis, namely that the above factors actually affect. This is also indicated by the small value of MCP in reference to an accepted well value of 3 for two factors and 4 for 3 factors. Moreover, since R2 exhibited maximum value of 2.92, only a small percent of the total variance (<3%) can be described by a linear model of the three factors of Table 7.
| Step | 1 | 2 | 3 |
|---|---|---|---|
| Constant | 1.438 | 1.467 | 1.487 |
| Wall Contact- Con | -0.070 | -0.072 | -0.073 |
| T-Value | -1.34 | -1.38 | -1.40 |
| P-Value | 0.182 | 0.168 | 0.162 |
| Level- L | -0.048 | -0.055 | |
| T-Value | -1.35 | -1.52 | |
| P-Value | 0.178 | 0.131 | |
| Wall's material- W | -0.040 | ||
| T-Value | -1.09 | ||
| P-Value | 0.276 | ||
| S | 0.337 | 0.336 | 0.336 |
| R2 | 1.09 | 2.20 | 2.92 |
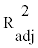 |
0.48 | 0.99 | 1.11 |
| MCP | -1.2 | -1.0 | -0.2 |
Table 7: Stepwise Regression: log (C) versus all factors. Value of Alpha-to- Enter was 0,5 and of Alpha-to-Remove 0,5. P-values represent calculated error probabilities and T-values, the corresponding values of t-student's test for the comparison of a P-value with a. The constants of the linear fit at each step are shown in first row. Bold values represent the corresponding slopes of each factor at each step. MCP is the Mallow's Cp.
According to data presented so-far, no single factor or linear subset of factors, could describe sufficiently the variance of the analysed radon concentration data. This implies that a multivariate set of factors could be probably more adequate. Table 8 presents the unrotated four principal factor loadings together with the corresponding communalities according to principal component analysis, applied, however, to radon concentrations. It is very interesting that, although factor 1 is loaded to five factors (bold numbers), the remaining three are only loaded to one single independent factor each. More specifically, 16.2% of the total variance may be described by factor 2 loaded only to the construction year. 12.3% of the total variance could be attributable to factor 3 loaded mainly to the existence of basement and 10.9% to the existence of contact (factor 4). A very important finding of Table 8, however is that since the loadings of factor 1 to “Level- L”, “Building Type” and “Construction Year- Y” are negative in respect to the one of C, it is rational to accept that concentrations would increase as Level, Building Type and Year are decreased. According to Table 3, this implies that ground floor dwellings tend to present higher radon concentrations. This is rational, since the lower the floor, the higher is the contribution of soil’s exhalation in indoor radon. Also detached houses tend to present higher concentrations, since other types offer pathways for radon’s interchange between dwellings in contact. Significant is also that aged dwellings, especially those of the previous century, presented higher radon concentrations. The latter finding is also reinforced by the positive loading of the “Wall’s material- W”, especially due to its rather high loading. Since higher wall values correspond to rock materials, it can be supported that higher concentrations are addressed in dwellings of the beginning of the twentieth century made of rocks. To some degree these results were supported by Table 7, since the dwelling’s “Level- L” and building “Wall’s material- W” were considered to be more significant compared to other factors.
| Variable | Factor 1 | Factor 2 | Factor 3 | Factor 4 | Communality |
|---|---|---|---|---|---|
| C | 0.178 | 0.104 | 0.444 | -0.415 | 1.000 |
| Area- A | -0.463 | -0.156 | -0.480 | 0.061 | 1.000 |
| Level- L | -0.588 | -0.415 | -0.157 | -0.44 | 1.000 |
| Ground Type- G | 0.242 | 0.410 | -0.498 | 0.026 | 1.000 |
| Basement- Bas | 0.291 | 0.405 | -0.646 | -0.111 | 1.000 |
| Building Type- BTy | -0.647 | -0.416 | -0.236 | -0.204 | 1.000 |
| Year- Y | -0.527 | 0.598 | 0.088 | -0.119 | 1.000 |
| Wall Contact- Con | -0.123 | -0.386 | 0.000 | 0.750 | 1.000 |
| Wall's material- W | 0.690 | -0.428 | -0.213 | -0.127 | 1.000 |
| Floor's material- F | 0.548 | -0.472 | -0.080 | -0.266 | 1.000 |
| Variance | 2.2225 | 1.6241 | 1.2337 | 1.0891 | 10.0000 |
| % Var | 0.222 | 0.162 | 0.123 | 0.109 | 1.000 |
Table 8: Unrotated factor loadings and communalities for 4 principal factors. The factor correlations exceeding the cut-off limit of 0.5 are marked in bold.
The statistical methods employed in this paper, revealed significant tendencies on potential ways that certain factors may affect indoor radon concentrations in Greece. These methods were applied to a large data-set of the principal indoor radon large-scale survey in Greece with passive dosemeters. The following important results were extracted:
(1) Approximately 95% of the measured log (C) values followed normal distribution, i.e., the vast majority of C values followed the lognormal distribution.
(2) About 0.1% of the investigated dwellings exhibited outlier radon concentrations.
(3) The majority of log (C) values exhibit residuals consistent with C values between 10 – 120 Bq.m-3.
(4) Under the view of MCP, only a combination of all factors except factor G (Ground Type) constitutes an acceptable subset that could minimise total bias. Hence under this view, no certain factor tendencies were found.
(5) According to ANOVA, lower level dwellings presented higher mean-annual indoor radon concentrations.
(6) T-test on ground and upper floor dwellings, showed that ground floor dwellings presented higher mean annual indoor radon concentrations.
(7) ANOVA statistics revealed a tendency of higher concentrations of rock dwelling.
(8) No single factor or linear subset of factors described sufficiently the variance of the analysed radon concentration data
(9) According to PCA, detached houses tend to present higher concentrations and that aged dwellings, especially those of the previous century, presented higher mean annual indoor radon concentrations.
(10) Significant differences were detected in results produced by some of the applied statistical methods.
New methods and, most importantly, more passive measurements of mean annual indoor radon concentrations in Greece, will assist the future research in this field. It is important that these future measurements will account, at least, the presented factors and associated levels and, preferably, include additional surveyed factors. It should be noted however, that this work constitutes only a first approach of this type. Focused studies accounting the role of certain factors in controlled dwellings, or, active multi-level measurements, will improve the methods and provide new pathways for assessing the effects of certain factors in indoor radon accumulation in Greece.
This research has been co-financed by the European Union (European Social Fund – ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF) - Research Funding Program: THALES Investing in knowledge society through the European Social Fund.