Journal of Defense Management
Open Access
ISSN: 2167-0374
ISSN: 2167-0374
Research Article - (2018) Volume 8, Issue 1
In this research the feasibility of the Holos Highly Integrated Micro Modular Reactor (HI-MMR), developed by Filippone and Associates LLC, is studied as a power source for military ground deployment. The Holos HI-MMR is a thermal gas-cooled reactor designed to generate 30 MWt. A model of the reactor was created in the Monte Carlo N-Particle code MCNP 6.1 to obtain the basic parameters of criticality and an estimate of burnup. The reactor design uses tristructural-isotropic (TRISO fuel), which was modeled as a homogeneous mixture at ten percent enrichment. At ten percent 235U, the k-effective value of the reactor was found to be 1.05810 ± 0.00166 at beginning of life (BOL). Based on burnup calculations, the reactor will last 13 years before requiring refueling. A value comparison to current configurations of diesel generators used in forward military operation bases was then performed using a baseline of $7 per gallon of diesel. In a case study of Bagram airfield, the Holos reactor was found to have a value of 7.03 out of 10 versus the current diesel generator configuration, which had a value of 4.15. Both of these values are found against criteria developed in this paper.
Keywords: Kenneth S Allen; Samuel K Hartford; Gregory J Merkel
AEPI: Army Environmental Policy Institute; BOL: Beginning of Life; CR: Conversion Ratio; EOL: End of Life; FOAK: First of a Kind; FOB: Forward Operating Base; HET: Heavy Equipment Transport; HEX: Heat Exchanger; HI-MMR: Highly Integrated Micro Modular Reactor; ISO: International Organization for Standardization; kWe: Kilo-Watt Electric; LVSR: Logistics Vehicle System Replacement; MCNP: Monte Carlo N-Particle Transport Code; MWe: Mega-Watt Electric; NOAK: Next of a Kind; NPV: Net Present Value; ORC: Organic Rankine Cycle; PCU: Power Conversion Unit; PWR: Pressurized Water Reactor; TRISO: Tristructural-isotropic fuel
The purpose of this research was to study the Holos Highly Integrated Micro Modular Reactor (HI-MMR) developed by Filippone and Associates LLC in order to assess the feasibility of modifying the reactor into a configuration suitable for military applications in forward deployed environments. The primary motivation for the project stems from the inherent dangers, logistical complexities, and overwhelming costs of the military’s current method of sustaining Forward Operating Base (FOB) power demands using diesel generators. Studies conducted by the Army Environmental Policy Institute (AEPI) found that every fuel resupply convoy in Iraq sustained an estimated 0.026 casualties while each convoy sustained 0.042 casualties in Afghanistan [1]. Furthermore, the U.S. Army Corps of Engineers’ Engineer Research and Development Center estimated that diesel generator fuel can cost up to $400 per gallon, and that the typical power demand of FOBs equates to 1.7 to 2.4 gallons of generator fuel per person per day [2]. While $400 per gallon is extreme, it is reasonable to estimate $7 per gallon in a forward deployed environment considering the logistical resources needed to transport the fuel to the user. The analysis performed in this research serves an important preliminary step in an attempt to replace or supplement the diesel generators in order to help reduce combat casualties and power costs (Figure 1).
Several private corporations and government agencies have expressed interest lately in revisiting the concept of small modular reactors for various purposes. Recently one of the proposals to the Defense Advanced Research Projects Agency (DARPA) was a thorium-fueled small reactor for military uses. The prototype reactor was ultimately not selected in favor of the Digital Manufacturing Analysis, Correlation and Estimation (DMACE) Challenge [3]. The reactor did receive strong support from DARPA. One special feature of the proposed thorium design was its potential to use used nuclear fuel wastes along with thorium to produce power and reduce longlived actinides. This fuel mixture would help to reduce requirements for high-level radioactive waste material disposal.
The use of reactors for the destruction of nuclear waste has been widely studied and supported particularly with fast burner reactors [4]. Although not part of this research, the TRISO fuel used in the Holos design could be modified to incorporate transuranic materials. In 2009, the International Atomic Energy Agency reported that, “Some development has taken place in the area of gas cooled thermal spectrum reactors for transmutation. Very high burnups of fissile material have also been obtained using TRISO coated plutonium mixed oxide with carbon and in uranium and plutonium mixed with thorium” [5].
The first step in the analysis was to create an accurate and detailed model of the Holos reactor. A series of calculations were made using the Monte Carlo N-Particle code (MCNP 6.1) to assess key performance parameters of the Holos design. The output of the MCNP calculations provided a baseline metric to perform a value comparison between the Holos reactor and currently implemented diesel generator configurations. Due to the distinct nature of these two processes, the methodology and results of the reactor model in MCNP 6.1 are presented separately from the methodology and results of the valuebased comparison. Following these sections, conclusions and further recommendations are presented reflecting the overall assessment of the suitability of the Holos design in forward operations.
Although the use of modular reactors in the Army has yet to be realized, the continuous operation of a nuclear U.S. Navy since the 1950’s establishes a precedent for the military use of nuclear power. Due to the potentially hostile adverse nature of the environments into which the Holos reactor could be deployed; design safety, resiliency, and transportability are important factors. Such design criteria were analyzed in the value comparison.
MCNP 6.1 model of holos design
The Holos reactor is a proprietary design created by Filippone and Associates LLC [6]. Information provided by the company dictated the design specifications and assumptions used in the development of the reactor model. The reactor consists of a cylindrical array of fuel subassemblies around a central control sleeve. The number of subassemblies in the core can be varied to meet specific power demands. Each fuel subassembly consists of a lattice of individual fuel and coolant channel cells surrounded by a cylindrical layer of steel serving as the primary pressure vessel. A summary of key parameters for the fuel subassembly and reactor are provided in Table 1. An axial view of the reactor core, the fuel subassembly and a zoomed-in view is shown in Figure 2.
| Parameter |
|---|
| Subassembly outer radius, cm |
| Subassembly height, cm |
| Steel pressure vessel, thickness, cm |
| Number of fuel channels |
| Fuel matrix, hexagonal pitch, cm |
| Fuel matrix, height, cm |
| Fuel region, radius, cm |
| Fuel region, height, cm |
| Coolant channel, radius, cm |
| Outer core wall, radius, cm |
| Outer core wall, thickness, cm |
| Core height, cm |
| Number of subassemblies |
| Subassembly pitch, cm |
| Control sleeve, radius, cm |
| Control sleeve, thickness, cm |
Table 1: Summary of Holos fuel subassembly and reactor parameters.
Figure 2: Axial view of Holos reactor core, with zoomed-in view of fuel subassembly and fuel channel matrix. In each view the TRISO fuel is light blue, the carbon moderator matrix is dark blue, the subassembly pressure vessel is red, the helium coolant is yellow, and the reactor pressure vessel is green.
Individual fuel channels were arrayed in a lattice structure according to information from the Holos design parameters. Small coolant channels were placed at the hexagonal vortices of the coolant channel. The coolant in the MCNP model is helium gas. The subassemblies were placed in a hexagonal lattice structure surrounded by helium coolant and the reactor’s steel pressure vessel. Note that the particular arrangement of 78 subassemblies is just one possible arrangement of the Holos HI-MMR design. In Figure 2, the fuel subassemblies can be seen arrayed around the central control sleeve, modeled as steel. The subassemblies and the helium coolant, in yellow, are surrounded by the reactor pressure vessel, shown in green, which is modeled as beryllium oxide to serve as a neutron reflector.
Assumption for reactor model
Several assumptions were necessary for creation of the core model. Of foremost concern were the composition, density, and disposition of the tristructural-isotropic (TRISO) fuel. TRISO fuel, is a relatively novel fuel design wherein fissile fuel is coated in layers of silicon and carbon which provide both moderation and containment of the fuel. For the model, the fuel is assumed to contain uranium dioxide, silicon carbide, and pyrolytic carbon. These materials were provided as part of the Holos design and are commonly used in the construction of TRISO. For purposes of simplicity, the TRISO is considered to be a homogeneous mixture of the materials, rather than modeled as discrete pellets. Modeling the discrete fuel pellets would require much greater effort than a homogeneous model, while previous work has shown that a homogeneous model produces very similar results to a discrete model [7]. The 235U enrichment was assumed to be ten percent, a viable enrichment level that still proves resistant to proliferation. The weight percentages of each element, calculated using the designdictated geometry of the fuel, an assumed ten percent fuel enrichment, and nominal densities of the materials are provided in Table 2. An important design parameter of the homogeneous fuel mixture model is the density of the fuel. Using an assumed packing fraction of 0.4 and the volumes and densities previously found to determine the weight percentages of each isotope, the density of the homogenous fuel mixture was calculated to be 3.49 g/cm3.
| Isotope/Element | Weight Percent |
|---|---|
| 235U | 0.081569 |
| 238U | 0.734120 |
| Carbon | 0.044720 |
| Silicon | 0.029807 |
| Oxygen | 0.109784 |
Table 2: Isotopic weight percentages in Modeled TRISO fuel.
Additional assumptions were made regarding the other materials within the reactor. The steel used in the reactor was modeled as 316 stainless steel [8]. This is a readily available steel but can be changed to reflect later design decisions. The helium coolant was modeled at a density of 0.001 g/cm3. The beryllium oxide shell was defined at a nominal density of 3.01 g/cm3. Lastly, the fuel matrix containing the TRISO pellets was modeled as graphite at a density of 2.266 g/cm3.
Model calculations
The first calculation performed on the model determined the k-effective value. This was accomplished using a KCODE calculation in MCNP6.1. The model did not have control elements in place- no control rods or burnable poisons. The KCODE calculation performed 100 cycles and discarded the first 50 to ensure statistical checks passed. The core model was run on a single dual-processor PC and took 6 minutes to complete.
Following the initial k-effective calculation, a burn-up calculation was conducted to determine the lifetime of the reactor. The BURN card in MCNP 6.1 calculates the k-effective value of the reactor at specified time steps, adjusting the composition of the reactor at each step to reflect changes in quantities of fuel and decay products, some of which are reactor poisons. The burn simulation was conducted at a reactor power of 30 MWt. The simulation was carried out until the excess reactivity was depleted and the k-effective value was less than 1.0 indicating the reactor would need to be refueled.
A final calculation to determine the temperature coefficient of the fuel sub-assembly was performed at beginning of life (BOL). The temperature coefficient indicates whether the criticality of the subassembly will increase or decrease with a change in temperature. A negative temperature coefficient is a critical design criterion since it provides a negative feedback response and promotes a stable reactor operation. If the design has a positive fuel temperature coefficient, the criticality will increase as temperatures rise thus increasing the possibility for fuel meltdown. This is especially dangerous in a solid moderated reactor, such as the Holos design, where a loss of coolant accident will not create a loss of moderator.
Criticality
The k-effective value of the reactor with a fuel temperature of 900 Kelvin was calculated to be 1.05810 ± 0.00166. This indicates that the reactor, when freshly fueled, has an excess of criticality, and is therefore feasible as a nuclear reactor. The excess reactivity can be reduced by various control methods, such as the central control rod, drum leakage, and geometric rearrangement of the fuel subassemblies, to maintain a critical state. As the reactor depletes its fuel supply, the control measures are progressively removed, extending the lifetime of the fuel within the reactor until such time that the reactor contains no excess criticality and must be refueled. Although the excess reactivity is significantly less than the value in the range of 1.4 for larger reactors, the Holos design contains significantly less fuel than a typical large pressurized water reactor (PWR). Also, unlike the right cylindrical core of a PWR, the Holos reactor core is a long narrow cylinder with significantly more leakage. Based on the fuel composition and geometry, the calculated k-effective value appears valid.
Burnup
A summary of the burnup results is presented in Figure 3. From the burnup data, the End of Life (EOL) was determined when the reactor’s k-effective was less than 1.0. For actual operation, if the k-effective value was greater than 1.0, the neutron control measures are used to maintain the reactor at a critical state. When the k-effective value reaches 1.0, all neutron control measures are fully removed, and further burnup would lead to a subcritical reactor. It is at this point at which the reactor would require refueling.
The burnup data was less linear when compared to large PWR models. Within the first 100 days of operation, the reported k-effective value of the reactor rose above its initial value. This result is linked to the low power level used in the burnup calculation, low leakage in the model, and the high conversion ratio (CR) in the reactor core creating fissile 239Pu. The high CR is due to the carbon moderation and low thermal neutron absorption in the helium coolant. As a check, an additional burnup run conducted using a reactor power of 500 MWt yielded a more expected, near-linear decline of the effective k value in the first 500 days of operation. When the idealized 30 MWt reactor was depleted out to EOL, the overall trend of the depletion curve, presented in Figure 3, is near-linear. The burnup presented in Figure 3 shows a reactor lifetime between 35 and 40 years. However, this an idealized model with very low leakage and no parasitic absorption in control elements. Based on the depletion of the reactor core at an operating power of 30 MWt, adjusted for actual operating conditions, the estimated reactor lifetime was determined to be 13.096 years.
Fuel temperature coefficient
The fuel temperature coefficient was calculated by varying the fuel temperature of the design and recording the resultant k-effective value. For this calculation, the temperature was varied between 293.6 and 2500 Kelvin by changing the cross-section libraries referenced by the fuel materials. The five libraries used correspond to temperatures of 293.6, 600, 900, 1200, and 2500 Kelvin. The results of the five MCNP runs are presented in Table 3. The k-effective values were plotted versus the fuel temperature and a trend line was fitted to the plot of data. An estimate of the fuel temperature coefficient is the slope of the trend line. The results of the computation are summarized in Figure 4.
| Nuclide Library | Temperature (Kelvin) | k-effective | Standard Deviation |
|---|---|---|---|
| 0.70C | 293.6 | 1.09402 | 0.00179 |
| 0.71C | 600 | 1.07247 | 0.00148 |
| 0.72C | 900 | 1.05810 | 0.00166 |
| 0.73C | 1200 | 1.04544 | 0.00190 |
| 0.74C | 2500 | 1.01461 | 0.00160 |
Table 3: K-effective of Holos reactor at various temperatures.
The temperature coefficient for the reactor was found to be -0.0000338 (Δk_eff)/K with an error of ± 0.000005 (Δk_eff)/K. The R2 for the trend line was 0.93. The result of the temperature coefficient calculation demonstrates that the reactor has a negative temperature coefficient, meeting a key design criteria.
A negative temperature coefficient is to be expected for a uraniumfueled thermal reactor. As temperature increases, Doppler broadening increases the overall area of the resonance region of the neutron cross section of heavy isotopes –most notably 238U. This increase in resonance absorption cross section results in a decreased number of thermal neutrons causing the resonance escape probability to decrease. Based on this knowledge, the calculated fuel temperature coefficient appears valid.
Value Analysis of Holos in Forward Operations
Using the Holos reactor lifetime and power data generated in MCNP, a comparative analysis was conducted in order to assess both the economic and operational viability of powering FOBs with Holos reactors rather than the current method of diesel generators. This comparative analysis was conducted primarily in two parts: cost comparison and operational value. In both parts, Bagram Airfield,Afghanistan served as the baseline against which the generators and the Holos were directly compared. Before describing the approach taken in conducting the value analysis, it is first necessary to provide some technical information regarding Bagram’s current state of power demand and supply.
Bagram’s power demand is 56 MWe which it provides using fifteen generators with power ratings ranging from 1-10 MWe, as summarized in Table 4 [9-18]. The power ratings shown in Table 4 include both the manufacturer’s ratings as well as the derated values given by the company contracted for transporting and installing the generators.
| Current Diesel Generator Requirements | |||
|---|---|---|---|
| Generator Type | Number Used | Power Rating (MWe) | |
| Manufacturer | Derated | ||
| Solar Turbine T-130 [16] | 4 | 15 | 10 |
| Solar Turbine T-70 [17] | 1 | 7.52 | 6 |
| PowerBox 20x [18] | 10 | 1.12 | 1 |
| Proposed reactor and generator combination | |||
| Reactor/Generator Type | Number Used | Power Rating (MWe) | |
| Manufacturer | Derated | ||
| Holos | 4 | 13.5 | 13.5 |
| PowerBox 20x [18] | 10 | 1.12 | 1 |
Table 4: Holos and generator configuration to Power Bagram Airfield (56 MW Demand).
Table 4 also summarizes the proposed Holos reactor configuration required to satisfy Bagram’s 56 MWe power demand and is based upon the MCNP core model results which found the Holos power output at 10% enrichment to be 13.5 MWe over a lifetime of 13 years. The configuration includes two diesel generators for emergency and essential services. The information summarized in Table 4 serves as the basis for the cost and value analyses conducted for the Bagram Airfield case study.
Assumptions for value analysis
Several assumptions were necessary in conducting this comparative analysis. The first being that all of the information regarding the Holos unit’s size, weight, and cost provided by Filippone and Associates LLC was assumed to be correct. These values are summarized in Table 5 which shows the Holos unit cost breakdown, and Table 6 which lists the Holos weight and the dimensions of the standard 20 foot ISO shipping container which houses the reactor [11]. The data provided by Filippone and Associates presented in Table 5 is for a 22 MWt and 10 MWe setup. The costs used in value analysis were adjusted to match the MCNP analysis of 30 MWt and 13.5 MWe. Table 6 also includes the manufacturer’s power rating, dimensions, and weight of each of the three generators evaluated in this project. The value analysis used the Next of a Kind (NOAK) costs for comparison with the addition of an estimate the fuel costs at 10% enrichment. The combined value was approximately $40,000,000. Much of the costs associated with the First of a Kind (FOAK) development of the Holos reactor are currently being realized in the development of the reactor components for nonnuclear applications- specifically train engines. The annual fuel costs are from the FOAK fuel supply divided over the lifetime of the core.
| LWRs | Holos Quad | FOAK | FOAK* | NOAK | |
|---|---|---|---|---|---|
| Equivalence | Cost Item | Amount | % of Total | Amount | Amount |
| Site Preparation | Site shielding and process heat | $660,000 | 0.4% | - | - |
| Nuclear Island | Integral core (fuel cartridges and heat exchangers) | $26,607,866 | 14.5% | $26,607,866 | $11,973,540 |
| Turbine Island | Power Conversion Unit (PCU) | $16,129,126 | 8.8% | $16,129,126 | $12,903,300** |
| Balance of Plant | Balance of Plant | $0 | 0.0% | $0 | $0 |
| Auxiliaries | Additional Plant Equipment (ISO HEX & Control) | $7,729,160 | 4.2% | $7,729,160 | $1,545,832 |
| Fuel Supply (22MWth) | $4,567,000 | 2.5% | |||
| Licensing & Engineering | $114,090,092 | 62.2% | $5,000,000*** | ||
| Other Costs & Contingencies | $13,582,659 | 7.4% | |||
| Decommissioning Costs | $625,796 | $625,796 | |||
| TOTAL CAPEX | $183,365,903 | 100% | $51,091,948 | $32,048,468 | |
| ORC coupling | Quad Intermediate HEXs, pumps, turbo-gens | - | - | $2,000,000 | - |
| - | $/kWe | MWe net | $/kWe | $/kWe | |
| Overnight Cost $/kWe | $18,337 | 10 | $5,109 | $3,205 | |
| Overnight cost $/kWe with ORC | $15,046 | 12 | $4,309 | $2,601 | |
Table 5: Holos single unit cost breakdown [6].
| Type | Power Box 20x[13] | Solar T-70 [17] | Solar T-130[16] | Holos[6] |
|---|---|---|---|---|
| Power Rating (MWe) | 1.12 | 7.52 | 15 | 13.5 |
| Length (m) | 6.058 | 11.9 | 14 | 6.058 |
| Width (m) | 2.438 | 2.9 | 3.2 | 2.438 |
| Height (m) | 2.591 | 3.7 | 3.9 | 2.591 |
| Weight (kg) | 16879 | 62935 | 86900 | 22680 |
| Fuel Consumption (gph) | 58.6 | 399.9 | 797.7 | N/A |
| Project Cost per Unit ($) | 415,520 | 2,789,920 | 5,565,000 | 40,000,000 |
Table 6: Generator and Holos specifications.
Because the unit and installation costs of the generators used in this project were either not publicly released or difficult to ascertain, other studies were used that indicated a project cost of $371/kWe was reasonable to assume.[12] This so-called ‘project cost’ accounts for both the unit and installation costs of the generators. This allowed an assumed single unit cost for each generator by multiplying the project cost value ($371/kWe) by the power output rating of each generator (i.e. 15,000 kWe for the T-130). These single unit project costs for each generator are included in Table 6. Generator maintenance costs were assumed to be $1.70/kWe per year. This assumption was based upon one study’s finding that the 20-year Net Present Value (NPV) maintenance costs for the diesel power plants studied was $33.71/kWe [12]. Since the analysis is focused on the annual maintenance cost and not the 20-year NPV cost, the report’s $33.71/kW is divided by 20 years in order to calculate the maintenance cost of $1.70/kWe per year. This maintenance cost is only applicable to the diesel generators and not to the Holos since no data was found to reasonably estimate the maintenance costs of a micro modular reactor.
In order to simplify the cost model, all generators were assumed to be operating at 75% load. This assumption was necessary since fuel consumption varies with the load experienced by the generator. Using this assumption, the fuel consumption of each generator was found. The only manufacturer that provided raw data on fuel consumption was the PowerBox 20x [13]. Therefore, the fuel consumption of the Solar T-70 and T-130 were based on their power ratings using an online calculator [14]. The fuel consumption, in gallons per hour (gph), of each generator is summarized in Table 6. Finally, a diesel fuel cost of $7 per gallon was assumed, which one report found to be a reasonable estimate [15].
The next set of assumptions used in the analysis involved the combat aspect of the model. That is, sustainment operations in the form of fuel resupply convoys and the casualties sustained in conducting such operations. Referencing a study conducted by the Army Environmental Policy Institute, we assumed a casualty factor of 0.042 casualties per fuel resupply convoy. Additionally, we assumed a standard fuel capacity of 128,000 gallons per fuel resupply convoy based off of the same report (16 trucks at 8,000 gallons each) [1].
General approach for value analysis
Cost comparison: The cost comparison portion of the analysis aimed to answer one question: When would it become more economical to use the Holos rather than the current diesel generator configuration to power Bagram Airfield? To answer this question, the total cost of both the current power method of diesel generators and the proposed Holos configuration presented in Table 6 were calculated according to Equation 1.
Total Cost=Project Cost + Fuel Cost + Maintenance Cost (1)
The project cost was calculated by multiplying the Project Cost per Unit values from Table 6 by the Number Used values from Table 4. The maintenance cost was determined by multiplying the assumed annual maintenance cost of $1.70/kW by the power produced by diesel generators in both the current and proposed methods. The fuel cost was obtained by calculating the total amount of fuel used per generator per day, summing this quantity to determine the total number of gallons of fuel used each day, then multiplying by the assumed fuel cost of $7 per gallon. Using the results of these calculations and Equation 1, a cost function was created for both the generator and the Holos configurations which are shown in Equations 2 and 3, respectively.
Total Cost=29,205,120 + n(702,053) (Generator Cost Function) (2)
Total Cost=205,201,644 + n(19,701) (Holos Cost Function) (3)
In these equations, n is the number of operating days, and the values inside the parenthesis are the sum of the maintenance and fuel costs since both of these costs were modeled to represent a daily expense. The cost function for the Holos configuration in Equation 3 includes the use of two Powerbox 20 diesel generators. Using Equations 2 and 3, the total costs of both the current and proposed methods were calculated and iterated over time in order to identify when the Holos option would become more economical. The results of this iteration are plotted in Figure 5. From Figure 5, the cost model demonstrates that the Holos option would become more economical after 250 days. This means that the Holos option would break even with the generator option at twice this cost intersect time, or 500 days.
Operational value model: The operational value model of our analysis determined which of the two power plant options was a better overall value with respect to electrical production in a deployed environment. Five value measures were considered in conducting this analysis: Single unit project cost per MWe, annual diesel fuel cost, projected annual number of combat casualties from fuel resupply convoys, projected annual number of sustainment convoys, and number of aircraft or vehicle platforms capable of transporting the power plant. Each value measure was then assigned a weight characterizing its degree of importance to the overall value of the system. Figure 6 is a swing weight matrix depicting how each value measure was weighted in the analysis.
The first value measure, unit cost per MWe, was derived by dividing the single unit project cost of the reactor or generator by its power output. Since three different diesel generators were evaluated, the sum of their respective project costs was divided this by the sum of their respective power outputs. The second value measure, annual diesel fuel cost, was calculated simply by multiplying the daily fuel costs calculated by 365 days. The third value measure, projected annual sustainment operations, was calculated first by dividing the gallons of fuel consumed per day by the assumed 128,000 gallons carried per convoy in order to find the number of fuel resupply convoys per day. This number was then multiplied by 365 days to give the number of fuel resupply convoys per year. The fourth value measure, projected annual casualties sustained from fuel resupply convoys, was calculated by multiplying the number of fuel resupply convoys per year by the assumed casualty factor of 0.042 casualties per convoy. The last value measure, number of compatible transport platforms, was found by first obtaining the cargo space and weight limits of three different aircraft and two ground vehicles. This data is summarized in Table 7 [19-21].
| Dimension | Military Aircraft or Vehicle[19-21] | ||||
|---|---|---|---|---|---|
| C-5 | C-17 | C-130 | LVSR | HET | |
| Max Cargo Weight (kg) | 179169 | 140160 | 30390.69 | 20412 | 63560 |
| Cargo Compartment Length (m) | 44.0944 | 26.8224 | 15.5448 | N/A | N/A |
| Cargo Compartment Width (m) * | 5.4864 | 5.1816 | 2.413 | N/A | N/A |
| Cargo Compartment Height (m) * | 3.81 | 3.4544 | 2.59 | N/A | N/A |
Table 7: Aircraft and vehicle cargo weight and space limits.
With this data, the dimensions and weights of the generators and Holos from Table 6 were compared against the cargo space and weight limits from Table 7 to determine which systems were transportable by which platform. This conditional operation is summarized in Figure 7.
The results of the value measure calculations are summarized in Table 8. These results constitute the raw data for the two systems. However, since the model is not simply comparing the Holos to a single generator system, but to generators as a whole, the transport platform compatibility results from Figure 6 were averaged across all three generator systems. That is, the generators were collectively compatible with 6 out of the 15 assessments in Figure 7, or equivalently, 2 out of 5 transport platforms. Additionally, it was assessed whether or not each system was transportable by both air and ground platforms. Therefore, a similar average was taken to assess all three generators such that, since 2 of the 3 generators were compatible with both air and ground platforms, we treated the generators as a whole to share this compatibility.
| Variables | Casualties per Year | Unit Cost ($/MW) | Annual Fuel Cost ($) | Annual Sustainment Convoys | Number of Compatible Transport Platforms | Air and Ground? |
|---|---|---|---|---|---|---|
| Generators | 12 | 371,000 | 256,115,390 | 286 | 2 | Yes |
| Holos | 1 | 2,962,962 | 142,857 | 8 | 3 | Yes |
Table 8: Value measure raw data.
The next step in conducting the value model was to assign single dimensional values to the raw data from Table 8, then apply the normalized swing weight for each factor evaluated in order to calculate the total value according to Equation 4.
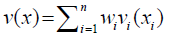 (4)
(4)
Where v(x) is the total value of the solution (generators or Holos), i=1 to n for the number of value measures assessed, x_i is the raw score of the solution on the ith value measure, v_i (x_i) is the single dimensional value of the solution on the ith value measure, and w_i is the normalized swing weight of the ith value measure. The results of this qualitative value model, illustrated in Figure 8, found a total value of 7.03 out of 10 for the Holos and 4.15 out of 10 for the generators.
Value Analysis
After conducting both a cost comparison model and a qualitative value model for the Holos and generators, the Holos option is a better overall value (7.25/10) than the generator option (4.15/10) in the Bagram Case Study. The Holos is economically competitive with the generator option after 500 operational days have elapsed. Since the results from of value model relied on the swing weights assigned to each value measure, a sensitivity analysis was performed to observe how the results would change when the swing weights of certain value measures were adjusted. For this analysis fuel cost and unit cost were the two value measures were analyzed. The results of this sensitivity analysis are presented in Figure 9. As shown in Figure 9, the value of the generators (Blue) never exceeds the value of the Holos (Orange) no matter how highly each value measure is weighted. This indicates that the results of the value model are reasonably valid.
After conducting both a cost comparison model and a qualitative value model for the Holos and generators, the Holos power plant option is a better overall value (7.03/10) than the generator option (4.15/10) in the Bagram Case Study. The Holos is economically competitive with the generator option after 500 operational days have elapsed. Therefore, the Holos is the better choice, if longer-term operation (greater than 500 days) is guaranteed.
The burnup calculations used to determine the life of the core were simple and the model did not include coupled thermal hydraulics. More detailed modeling of the reactor core is needed to verify the fuel consumption and power expected from the design. Additional research is also required for more case studies involving military operations outside of the Bagram Airfield. The variety of potential deployment environments is so varied that there are nearly unlimited scenarios of threat and locations combined with energy demands that can be examined to verify the usefulness of the HI-MMR concept for military ground use. However, there is no doubt that the demand for electricity independent of the host nation’s energy grid will continue to be an ever-increasing mission requirement in the future of modern warfare.
Filippone and Associates LLC provided their proprietary reactor design information necessary to complete the model and value analysis. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.