Sheehans [1] recently published his work on the dynamicallycontrolled steady state pressure gradient in a black body cavity. He derives pressure difference on two very chemically deferent surfaces, S1 and S2 (see in Figures 1-3). In his derivation the pressure differences are purely arises due to the different rate of dissociation and recombination of chemical species A2 and A in chemical reaction 2 A ⇔2Aon S1 and S2 surfaces. He claims that this dynamic pressure difference can be sustained in steady-states. Duncan [2] uses Sheehans pressure difference claims and predict that if this pressure difference really sustains then one can make a perpetual machines like turbines with apposite blades which can use this pressure difference and generates a net torque, and thus in principle it can keep rotating for ever without any external work on the system. Sheehans et al [3] performed experiments using tungsten and rhenium as S1, S2 surfaces (see in Figure 4) and claims that they have measured the temperature difference (equivalent to the pressure difference according to their definition) between the two surfaces. Sheehans et al [3] concluded (see conclusion section in3) that their result cannot be explained under current framework of 2nd law of thermodynamics and thus 2nd law of thermodynamics require a serious modification. In this paper we will discuss the shortcoming that exists in Sheehans [1], Duncan [2] and Sheehans et al [3] papers. We will only discuss the inaccuracy that exists in these papers.

Figure 1: Proposed Duncan’s device set-up.

Figure 2: Proposed Duncan’s device set-up.

Figure 3: Proposed chemical reaction on S1 and S2 surfaces.

Figure 4: Chemical reaction on tungsten (W) and rhenium (Re) surfaces in black body cavity.

Shortcoming in sheehans paper

Sheehans [1] during his pressure difference (ΔP=P1− P2) derivation has completely ignored the momentum of adsorbed gases on both S1 and S2 surfaces. He assumes that gases adsorb on both surfaces with effectively zero momentum (see equation 1) or he assumed that, first gas get absorbed (less than mono layer) and then he derived his pressure formula for desorb gases. This assumption is not valid for any equilibrium or non-equilibrium process at any temperature and pressure. So equation 1 (see1) has to be modified and includes at-least two extra term namely; pressure contribution due to molecule A₂ adsorption on S1 surface, and pressure contribution due to atoms.

An adsorption on S2 surface (see in Figure 1). So, two extra terms, 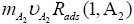and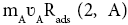 should have been added in equation 1 (see in1). In this equation Rads stands for rate of adsorptions of chemical species on the corresponding surfaces in per-second and in per-meter-square surface area. So, the final equation should have been written as,

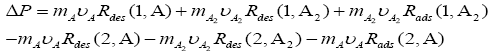(1)

At any temperature and pressure R_ads term should have been added on both S1 and S2 surfaces. It does not matter that whether reaction is in equilibrium or in non-equilibrium. If R_ads term drop in equation 1 (see in1), then there is no reason to believe that why R_des term should not be dropped, because ad- sorption and desorption is a thermodynamic process and it occur simultaneously in both equilibrium and in nonequilibrium situation. Only the rate constant term for the adsorption and the desorption process shall be different in chemical reaction A₂ ⇔2A A at S1 and S2 surfaces when reaction moves in either forward or in backward direction.

Shortcoming in duncan paper

Duncan in his paper 2 thought that pressure difference on two surfaces (see for example S1 and S2 surfaces in Figure 2) can rotate the turbine blades. He ignores that if there is net pressure difference on any system then there will be net force (ΔP × A, where A is the surface area of S1 or S2) on the system centre of mass. So system will not only rotates but translates as well. This system is very unstable in translational degree of freedom. So in this system no process will be cyclic and regain its original thermodynamics states after one complete rotation. Also the one part of total chemical energy of the system has been used to rotate the blades (rotational kinetic energy) and the other part of the chemical energy has been used for the translational kinetic energy of the center of mass of the system. If one assume that there will be some kind of holder which hold the turbines shaft, so that it cannot translate, then there will be a frictional force which arise between the holder and in turbine shaft. Then shaft will rotates against this frictional torques and thus a part of the chemical energy will waste against irreversible frictional work. If one thinks an ideal holder which does not generate a frictional torque between the holder and in turbine shaft, then it will be a complete absurdity because there will always a frictional force and thus frictional torque between any two material media. The frictional force arises due to quantum mechanical effect. Only static/kinetic frictional coefficients value can be minimized but it value can never become complete zero.

Now let see what Planck- Kelvin statement says about the second law of thermodynamics:

“The Kelvin Planck statement (or the heat engine statement) of the second law of thermodynamics states that it is impossible to devise a cyclically operating device, the sole effect of which is to absorb energy in the form of heat from a single thermal reservoir and to deliver an equivalent amount of work. This implies that it is impossible to build a heat engine that has 100% thermal efficiency” [4].

The first key point in Kelvin-Planck statement is the “cyclically operating device”. Second key point is “100% thermal efficiency”. Duncan’s device is irreversible noncyclic device. Also Duncan’s device is not 100% efficient, because only a fraction of the total chemical energy has been used in rotational process. Other part of chemical energy has been used in translational process. So “useful mechanical work” (for example lifting weight) will always be less than 100% available chemical energy. Therefore, no question of breaking the 2^nd law of thermodynamics arises in Duncan’s paradox

Shortcoming in sheehans et al Paper

There are number of shortcomings in this paper. We will go one by one. Sheehans et al [3] claims that they have measured two different temperatures on tungsten and rhenium metal surfaces in their black body cavity experiment (see in Figure 4). Since tungsten and rhenium are two different metals, they also have different crystal structure, different Brillouin zones, different electronic and phonon band structures, different surface orientations and different surface activation energy, there- fore, one should not surprise if tungsten and rhenium show different adsorption and desorption rates for same gas (He, and H₂ in this case). Also, dissociation and recombination reactions are endothermic and exothermic respectively, whose rate are material, temperature, pressure and surface specific, therefore, one should not surprise if two different temperature develops in the vicinity of two different metal surfaces. Also, development of different temperature in the vicinity of two surfaces does not guarantee that pressure difference will also be developed. Because if one use the ideal gas equation for pressure 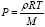then one notice that pressure is not only depends on the temperature but density and molar mass of the mixture gases as well. So, one need to calculate density of the gases and their effective molar mass in the vicinity of two metal surface (S1 and S2) before reaching any conclusion. Also, one mole of A2 gas dissociate and form 2 mole of A gas, so one must know the degree of the chemical reaction α, for A₂ ⇔2A in for- ward direction and rate constant to get the density and effective molar mass of the mixture gases. Because, on S2 surface (see in Figure 3) 2A atoms combines and form A₂ molecules. So, at S2 surface density of gas decreases and probably effective molar mass increases, but since reaction is exothermic, therefore, temperature of the gas in the vicinity of S2 surfaces will increases as well (Figure 5). Since gas pressure equation (take ideal gas equation) 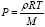is directly proportional to density and temperature but inversely proportional to the effective molar mass of the gases, therefore, it is extremely difficult to suggest or conclude that the gas pressure will also be different in the vicinity of two metal surfaces where the chemical reaction are taking place.

Figure 5: Molar mass in the vicinity of two metal surfaces (S1 and S2).

Let focus on sheehans et al [3] paper:

1) Sheehans et al wrote “Duncan argued that if these surfacespecific chemical activities were indeed possible, then stationary pressure gradients could arise between the radiometers apposing vane faces that could, in principle, be used to create a pressure engine that performs work perpetually at the expense of the surrounding heat bath, in conflict with the second law of thermodynamics”

Strictly speaking this statement is not correct because net pressure (ΔP=P1 − P2) will also give net force (ΔP × A, where A is the surface area of the surface S1 or S2, see in Figure 2), and thus whole setup will have translational degree of freedom, and thus very unstable (we have discussed it in previous section).

2)“Because the filament pair has identical dimension, comparable emissivities and coefficient of thermal conductivity, their radioactive and conductive loss were similar”

Rhenium has hcp and tungsten has bcc-crystal structures. Both have different crystal lattice parameter and different surface orientations. Both have different electronic and phonon band-structures. Electron and phonon band structures plays a very key role in electrical and in thermal conductivity. We don’t know on what fundamental basis Sheehans et al [3] have concluded that they share similar properties except that they are only metals. Different metals have very different surface orientation, surface area and surface activation energy on microscopic level where reaction takes place. Origin of physical and chemical properties of any material is purely arises due to quantum mechanical effects.

3) “According to standard thermodynamics, it is required for all temperature and pressure that ΔT_He=0 and

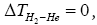but especially that 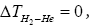this is the crux of Duncan’s paradox”

Strictly speaking, this statement is only correct when both filaments are made from same material. If both filament are made from the different materials as in Sheehans et al [3] case (W and Re), then thermodynamics doesn’t says that ΔT_He=0, 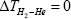and 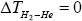In fact thermodynamics says that for any system macro- scopic average value of (ΔT_He), (ΔT_H2 ) and (ΔT_H2 −He) should be zero. In other words, (ΔT_He)=0, (ΔT_H2 )=0 and (ΔT_H2 −He)=0 for any thermo dynamical system. In this case the whole cavity should be treated as system, because surface coverage in cavity is very low (less than mono layer). And due to extremely low gas pressure in- side the cavity the thermodynamics rules are not applicable until one takes whole cavity as a thermodynamic system. Thermodynamics always talk about macroscopic average of any thermodynamics variable rather than few atoms or molecules. For example, temperature of one atom or one molecule does not make any sense, but temperature of few hundred thousand atoms or molecule does make sense.

4)“Thermal conductivity of helium is similar to that of H₂ and therefore can be used to estimate the convective loss in H₂”.

Thermal conductivity of He and H₂ are same on every crystal structure and every surface orientations? Answer is absolutely “No”. W and Re have different crystal structure, different lattice parameters and different surface orientations. Also, geometrical surface area is not the same as the microscopic surface area where adsorption and desorption are taking place unless both surface are made from same material.

5)“It also indicates that the concentration of H and H2 over two metals could not both have reflected gas-phase equilibrium value because equilibrium concentrations are unique for given temperature and pressure”.

Concentration is a macroscopic quantity and only average value of concentration in a certain volumes makes thermodynamically sense. So, in principle surface concentration should not reflect the equilibrium concentration.

6)“The difference in hydrogen dissociation power between the two metal coated thermocouple was relatively small, but their difference in power density was substantial A₂ ⇔2A. If this temperature difference were employed in a classic heat engine, it Carnot efficiency would be low but thermodynamically significant”

If one see Figure 3, then one notice that at S1 surface endothermic reaction, whereas on S2 surface exothermic reactions are taking place. Let’s take temperature of the system Ts. Then at S1 surface heat energy get absorbed by the A2 molecule and dissociate into 2A atoms. If this reaction perpetuate and there is no heat flow from the external agency (which maintained the system temperature at a fix value), then S1 surface will be cool down and it temperature moves toward zero kelvin in temperature scale. One should also know that the endothermic reaction is temperature dependent. Once temperature goes down then endothermic reaction will stop. Since S1 surface temperature maintained at T1, it suggest that there is a competition between thermal energy that come from external agency towards surface S1, and consumed in the chemical reaction A₂ ⇔2A by the A2 molecules to get dissociation into 2A atoms. So, indirectly it is the external agency which maintained the S1 surface temperature. Secondly, at S2 surface, there is heat flow from the S2 surface towards the external world through surface- coated tungsten wire (see in Figure 4). And thus S2 surface temperature maintain at T2. Therefore, temperature at S1 and S2 surfaces are maintained by the external agency. One should not confuse that heat releases at the S2 surface get consumed at the S1 surfaces. There is no-way through this is possible in any system. Surface S1 maintains it temperature by taking the heat energy come from the external agency which maintained the system temperature and pressure at a fix value. It seems to the author that Duncan [2] has thought that heat energy released at S2 surface can be used at the S1 surfaces during the endothermic reaction.

7) “If the standard theory of heterogeneous catalysis is valid, then the GF filament should not have been able to shift their H and H2 concentrations so far from equilibrium as was observed and not to distinctly different value in which case they should not have been able to display different hydrogen dissociation power consumption (Phd). This implies that ΔPhd should have been zero over entire temperature, pressure range investigated”

This statement is only correct if both filaments are made from the same material. In this case one filament is made from tungsten which has bcc-crystal structure and other filament rhenium has hcp-crystal structure. Both have different lattice parameters, different Brillouin zones, different electronic and phonon bands, different surface reactivity and different surface activation energies. One should not expect that they will behave exactly the same until they are perfectly identical in every aspect.

8)“This argument fails on at-least two count, first, a standard formulation of the second law, one not requiring heat engines, stipulates that isolated system (like a black body core) must relax to an equilibrium characterized by single temperature. The experimental DP system did not; rather, it maintained two distinct temperatures that did not and apparently could not-relax to a single temperature on account of its dual surface specific reaction rates. Apparently, the DP system constitutes stationary-states non-equilibrium”. First of all temperature is a macroscopic thermodynamic variables. Macroscopic thermodynamic variable always calculated by using the macroscopic average statistical rules. So, getting one value in macroscopic average calculation does not mean that same value is present all over the place in macroscopic volumes. It only suggests that the calculated value is the average value. So, standard thermodynamics does not say that same temperature should be present on both S1 and S2 surfaces. It says that if both the filaments (S1 and S2 surfaces (see in Figure 2) are made from the same materials) are same then the average temperature on both the surfaces should be the same, and it should be equal to the system temperature which is fixed by the external agency.

In this paper we have addressed the flaw that exists in Duncan’s paradox. We have shown that the dynamically-controlled steady-state pressure gradient or temperature- gradient is maintained by the external agency which controls the temperature and pressure in the black-body cavity. We have shown that the experiment done by Sheehen et al [3] does not violate the 2nd law of thermodynamics. We hope that this paper will clear the doubt about Duncan’s paradox and stimulate the scientific community to start looking the physical observations at microscopic levels.

Author is very grateful to Ashcroft and Mermin for their book on solid state physics.