Maxwell-demons was the thought-experiment by James Clerk Maxwell in 1867, in which he suggested that second law of thermodynamics can be violated if one able to segregate hot atoms/ molecules in one compartment and cold atoms/molecules in other compartment from an equilibrium system without performing any extra work [1-5]. Maxwell hypothesized a thought experiment and wrote “if we conceive of a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are as essentially finite as our own, would be able to do what is impossible to us. For we have seen that molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics” [6-11].

Several papers have been written in a favor, as well as against, to the Maxwell's-demon in various systems where the validity of second law of thermodynamics has been questioned/favored [12-34]. In this paper, we will provide a clear insight using standard thermodynamics rule, such as, thermodynamics potential, Gibbs free energy, and entropy, and will show that the Maxwell's-demon will never be able to break the second law of ther-modynamics any-day, and anytime. Before dealing this problem, let see how chemical-potential energy changes as a function of temperature and pressure. To make our analysis simple, we will use ideal gas system in our anal-ysis (without losing any generality). In an ideal gas, the chemical-potential is dened using the Gibbs-Helmholtz equation [37],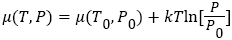 (1)

Where μ0 and P0 are the chemical potential and pressure at equilibrium, k is the Boltzmann constant, and T is system temperature in Kelvin. As we can see that, chemical potential μ (T, P), depends on temperature and pressure. As hot atom/molecule transfers from compartment A to compartment B (see in Figure 1), then, temperature and pressure in compartment B start increasing, while in compartment A, both starts decreasing from equilibrium value. As pressure and temperature changes in both compartments from equilibrium value, it shifts the chemical potential of atoms/molecules in both compartments. In compartment A, chemical potential start decreasing, because both pressure and temperature start decreasing after Maxwell’s demon intervention, while in compartment B, chemical potential start increasing, because, both pressure and temperature start increasing. Variation of chemical potential with pressure and temperature in both compartments can be written as, 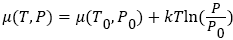Where μ0(T0, P0), is the equilibrium chemical potential of the gas. Similarly, the change in Gibbs free energy in each compartment A, and in compartment B, can be written as,

Figure 1: Schematic diagram of Maxwell’s-demon. Blue color atoms/ molecules correspond to low temperature atoms/molecules, whereas the red color correspond to high temperature atoms/ molecules [35].

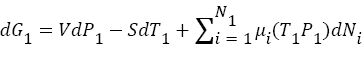(2)

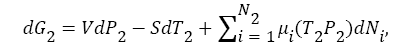(3)

Therefore, the net change in Gibbs free energy which will be available as a useful work can be written as,

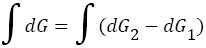(4)

This is a minimum amount of work which Maxwell's demon will have to performs on the gas-system during the segregation of cold and hot atoms/molecules in two different compartment A, and B respectively.

Maxwell wrote “For we have seen that molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform.” [9-11].

Temperature is a macroscopic average quantity. It is being calculated after statistical average of many particles having wide range of kinetic (Maxwell-Boltzmann velocity distribution. See for example N2, molecules velocity distribution in Figure 2) energy present in a certain volume, therefore, only average value of temperature in any small investigating volume which contains many numbers of particles (not few) make any sense in thermodynamics. So, there should not be any such term, like, “uniform-temperature” or “uniform velocities” in thermodynamics. However, average temperature or most probable velocity does make sense and these terms are perfectly valid.

Figure 2: Maxwell-Boltzmann speed-distribution of N2-molecules of air with temperature [36].

Maxwell further wrote “Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics ” [9-11].

There are two fatal flaws in this maxwell argument. First flaw is that, Maxwell thought that system will still remain in equilibrium all the time even after continuous segregating of hot (cold) atoms/molecules from one compartment A into another compartment B (see in Figure 1). System equilibrium property defines through its temperature, pressure, Gibbs free energy and chemical potential of constituent atoms/molecules at that temperature and pressure. All these characteristic properties of the system changes as temperature and pressure changes continuously during the segregation of hot (cold) atoms/molecules into different A (B) compartment (see in Figure 1). As the hot atoms/molecules start segregating in compartment B after demon intervention (see in Figure 1), temperature in compartment B start increasing, while temperature in compartment A, start decreasing from equilibrium value (see in Figure 1). As temperature start changing in both compartments, gas pressure in both compartment start changing as well (assume ideal gas equation)

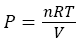(5)

Change in temperature and pressure in both compartment A and B, directly changes the chemical potential of the atoms/molecules in both compartments, which vary as a function of temperature and pressure, and can be written as,

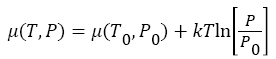
Where μ₀, and P₀, are the equilibrium chemical potential and equilibrium pressure of the atoms/molecules. In compartment A, as segregation of atoms/molecules started, (see in Figure 1) pressure and temperature start decreasing from equilibrium value, and thus, chemical potential also starts decreasing from equilibrium value μ₀(T₀, P₀). While in compartment B, (see in Figure) pressure and temperature start increasing from equilibrium value μ₀(T₀, P₀), and thus, chemical potential start increasing as well from equilibrium value μ₀(T₀, P₀). Thus, as the segregation of hot (cold), atoms/molecules started in different compartment A (B), by Maxwell’s-demon, the net change in chemical potential difference between two compartments A, and B also started as time progress. Thus, system no longer remain in thermodynamics equilibrium during the transition of the hot atoms/ molecules from the cold compartment A, into hot compartment B.

Second fatal flaw in Maxwell’s argument is that demon did not perform any work on the system, and able to segregate the hot atoms/ molecules in one compartment B (higher chemical potential), and cold atoms/molecules (low chemical potential) into other compartment A.

If one investigates the system closely, then, one notice that, there was always time varying finite chemical potential difference presented between hot compartment B, (higher chemical potential) and cold compartment A, (low chemical potential) during the segregation of the atoms/molecules into different compartments. This chemical potential difference was zero at the thermodynamics equilibrium. But, once the demons disturbed that thermodynamics equilibrium by allowing only one type of atoms/molecules in one compartment, and other type of atoms/molecules into other compartment, chemical potential difference start developing between the two compartments, A and B. This is a time varying chemical potential difference. Now, demon must work against this chemical potential difference to transfer any hot atom/molecule anytime from compartment A to compartment B. The minimum work done (during reversible equilibrium process at eachstep, every time) by Maxwell’s demon must be equal to change in chemical potential energy during the transition of hot atom/molecules from compartment A, to compartment B (see in Figure 1). Also, as hot atoms/molecules go in compartment B, temperature in compartment B start increasing, which increases the temperature of cold atoms/ molecules, present in compartment B as well, and thus, number of cold atoms in B start decreases (see Maxwell-Boltzmann speed distribution of N2 molecules of air as a function of temperature 2) as time progress. The minimum change in entropy in this process by Maxwell’s demon can be calculated as,

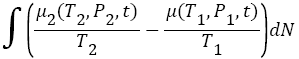(5)

where, T₂, P₂, T₁, P₁ are the temperature and pressure in compartment B and A respectively at any time t. And, dN is the number of atoms/molecules that has been transferred from compartment A to compartment B, by demon at each step, because, chemical potential of atoms/molecules in both compartment changes continuously as a function of temperature T, and pressure P, as hot atom/molecules transfer from compartment A to compartment B (see in Figure 1). Also, as time progress and demon transfer more and more hot atoms/molecules from compartment A to compartment B, the number of atoms/molecules in compartment B increases in comparison the compartment A (because cold atom in compartment B also get heated as temperature changes in B due to transfer of hot atom/molecule from compartment A (see the probability distribution profile in Figure 2). Thus, there will be an uneven distribution of atoms/molecules in both compartments rather than equal distributions (contrast to Maxwell guess). Also, more than half of total (including both compartment) atoms/molecules will be at higher temperature in compartment B, and, thus they will have higher entropy, compare to compartment A, atoms/molecules, which have low entropy. The total change in entropy of the system must be equal to the change in entropy of compartment B, plus change in entropy of compartment A, plus minimum entropy contribution due to Maxwell’s demons at each step when demon transfer hot atom/molecule from lower chemical potential (in compartment A) to higher electrochemical potential (in compartment B) using equation,

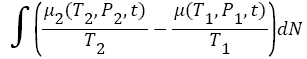
where T₂, P₂ are the temperature and pressure in compartment B, while T₁, P₁ are the temperature and pressure in compartment A, at any time t. As we see that compartment B, accumulates more and more chemical potential energy (Gibbs free energy if one count total chemical potential energy associated with total number of atoms/ molecules in compartment B) as time progress, at the expense of the Maxwell’s demon work. One can say that the whole of the Gibbs free energy that has been buildup in compartment B, has directly come from Maxwell’s demon work, and thus, no question for breaking of the second law of thermodynamics arises in Maxwell’s-demons paradox. Maxwell’s demon working principle can be visualized and simplified further if one compares it with the working principle of rechargeable battery using electricity. In electrochemical battery, certain type of ion/ molecules (depends upon the type of battery) move from cathode to anode and buildup higher chemical potential at anode during charging. As more and more ion/molecules move due to external agency (like external voltage source which recharge battery, or Maxwell’s-demon) which move ion/molecules from cathode to anode, higher and higher electrochemical potential buildup at anode. Once, almost all ion/molecule (maximum) which can be moved from cathode material towards anode material has moved, highest chemical potential difference buildup between anode and cathode. And thus, we call battery is fully charged now, and stored electrochemical energy in battery is available for performing any useful work. The same total stored electrochemical energy is also called Gibbs free energy (because Josiah Willard Gibbs in 1873 defined such energy as maximum “available energy” for any work. Josiah Willard Gibbs wrote “the greatest amount of mechanical work which can be obtained from a given quantity of a certain substance in a given initial state, without increasing its total volume or allowing heat to pass to or from external bodies, except such as at the close of the processes are left in their initial condition” [7]). Now, if one analyzes the working principle of a charging battery, then, one notice that, battery will “never” be able to charge itself without external intervention, such as external source which will create require potential difference between cathode and anode electrodes, and will assist in movement of ion/molecules from cathode to anode. In this case, external source performs at-least minimum amount of work, which is equal to the total electrochemical energy stored in the rechargeable battery. So, one can see that it is the external source, who has performed at-least minimum amount of work equal to the total electrochemical energy stored in the rechargeable battery. This is exactly what second law of thermodynamics wanted. As we see that the second law of thermodynamics does not violate in charging of the rechargeable battery. Similarly, in Maxwell’s-demon case as well, it is demon, who must work during the segregation of the hot atoms/molecules in one compartment, and cold atoms/molecules in another compartment. Also, demon work must be at-least equal (if demon able to work using reversible process) to the stored Gibbs free energy, which arises in the system once atoms/molecules get segregated into different compartments. Thus, the second law of thermodynamics does not violate in Maxwell’s demons case.

Till now we have discussed the case in which hot atoms/molecules have been transferred from compartment A, into compartment B. One can also discuss the other case in which demon will transfer cold atoms/molecules from compartment B, into compartment A. As demon start transferring cold atoms/molecules from compartment B, into compartment A, temperature in compartment B start increasing, because, there will be only fewer atoms/molecules in compartment B, whose temperature are below the average temperature (see in Figure 2). As low temperature atoms/molecules number decreases, average temperature of the compartment B, increases, which indirectly increases the temperature of low temperature atoms/molecules as well. Thus, the temperature in compartment B, will always increases in both cases, that whether hot atoms/molecules has been transferred from compartment A, into compartment B, or cold atoms/molecules has been transferred from compartment B, into compartment A. Also, as time progress, and temperature in compartment B increases, only very few atoms/molecules will remain in low temperature regime (see Maxwell-Boltzmann distribution of N₂ gas as a function of temperature 2). Due to rise in temperature in compartment B, pressure will also increase, and thus, chemical potential will increase in compartment B. While, in compartment A, temperature will decrease as more and more cold atoms/molecules come from compartment B, into compartment A. As time progress, hot atoms/molecules (present in compartment in A) temperature decreases as well. Also, pressure either increases or decreases in compartment in A, seems very ambiguous, because, if one use ideal gas equation, then, one notice that the gas pressure 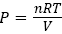, proportional to both density and temperature of the ideal gas. So, although temperature has decreases, but gas density has increases. How these two quantities (n and T) will effect the pressure need to be investigated further. It quite possible that the effect of temperature is more than the change in gas density, therefore, pressure may fall down. Also, effect of the pressure and temperature on chemical potential also need to be investigated. If both pressure and temperature fall down from equilibrium value, then chemical potential in compartment A, will decreases, and follows,

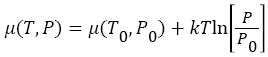
If pressure and temperature are interacting in such a way, that it increases the chemical potential in compartment A, then one need to calculate the overall chemical potential gradient between compartment A, and in compartment B. It seems to the author that there will be a chemical potential gradient between compartment A, and in compartment B, for cold atoms/molecules. And, thus demons must need to work on the system during the transfer of cold atoms/ molecules from compartment B, into compartment A. If one sees the change in Gibbs free energy in both compartment A, and B, then, one notice that,

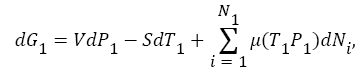
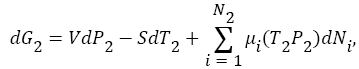
From both of these equations, it is clear that concluding anything in this case is extremely difficult. Because, change in Gibbs free energy in each compartment depends upon the change in pressure, change in temperature, change in atoms/molecules, and their chemical-potential as a function of temperature and pressure. It is quite possible that there will be a positive chemical-potential energy gradient exits between compartment A, and in compartment B, for cold atoms/molecules, when cold atoms/molecules transfers from compartment B, into compartment A. Because, chemical-potential also depends on the density of constituents (in this case cold atoms/molecules in compartment A, which increases from equilibrium value as more and more atoms/molecules transfers from compartment B, into compartment A). Thus, there will be a chemical-potential gradient between compartment A, and in compartment B, for cold atoms/ molecules, and thus, Maxwell's-demon must need to work against this chemical-potential gradient during the transfer of the cold atoms/ molecules from compartment B, into compartment A. Since, analysis in this case is very complicated, therefore, we assume that system will evolve in such a way that the total change

in Gibbs free energy (minimum work done by Maxwell's demon) will be equal to,

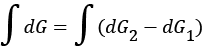
After evolution of the system, the Gibbs free energy which will be available for useful work is equal to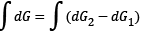

And thus, this 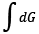will be the minimum amount of work (only possible with reversible process), which demon must need to work on the gas system during the segregation of hot and cold gas in two different compartments. One must consider cold compartment A, hot compartment B, and the total work done by the demon in-order to obtain the total change in entropy of the system. In other words, total change in entropy of the system can be written as,

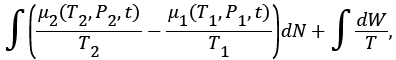
where dW is the deferential amount of irreversible work done by demon at temperature T, during the transfer of atom/molecule from one compartment into other.

In this paper, we have addressed the flaw that exist in Maxwell’sdemon paradox. We have shown that

due to chemical potential difference between hot compartment B, and cold compartment A, there is no way through which Maxwell demon can transfer hot atoms/molecules form cold compartment A, to hot compartment B, without performing any extra-work. Each time demon must perform atleast minimum amount of work, which is atleast equal to difference in chemical potential between hot compartment B, and cold compartment A, for each atom/molecule at that time. We have shown that as time progress, and demon continuously transfer hot atoms/molecules from cold compartment A, to hot compartment B, the chemical potential of hot compartment B, will increases, whereas cold compartment A, will decreases continuously. And, thus, there will be a chemical potential gradient develop between two compartment A, and B, which continuously increases till demon transfer last hot atom/molecule from cold compartment A, to hot compartment B. We have shown that demon must have to work against time varying chemical potential gradient each time during the transfer of hot atoms/molecules from cold compartment A, into hot compartment B. We have shown that demon must perform at-least total minimum work, which must be equal to change in Gibbs free energy between the hot and cold compartment after the end of the process (when hot and cold atoms/molecules segregated completely into two different compartments). We have shown that if system has reached in thermodynamics equilibrium, then there is no way through which Gibbs free energy (maximum available energy for work, E−TS) can be extracted further without any external source intervention. We have shown that there is inherent flaw in Maxwell demon thought experiment, and thus, this demon will never be able to segregate the hot atoms/molecules in one compartment B, and cold atom/molecules in other compartment A, without performing any extra-work on the system, and thus, this demon will never be able to break the second law of thermodynamics at any temperature or pressure.

We hope that this paper will clear the doubt about Maxwell’s-demon paradox and stimulate the scientific community to start looking the thermodynamics fundamentals equations at microscopic levels carefully.

Now, we can quote Arthur Eddington: “The second law of thermodynamics holds, I think, the supreme position among the laws of Nature. If someone points out to you that your pet theory of the universe disagrees with Maxwell's equations-then so much the worse for Maxwell's equations. If it is found to be contradicted by observation, well, these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics, I can give you no hope; there is nothing for it but to collapse in deepest humiliation” [25].