Forest Research: Open Access
Open Access
ISSN: 2168-9776
ISSN: 2168-9776
Research Article - (2015) Volume 4, Issue 3
It is generally agreed that preservation of forest areas can contribute strongly to the mitigation of global climate change. However, studies have demonstrated that there are still uncertainties for an accurate estimation of carbon stock particularly in the tropical forest. This study aims therefore to develop some allometric equations that can be used to estimate above-ground tree biomass and carbon partitioning between major carbon pools such as tree and litter for IITA secondary forest ecosystem. Ten permanent sample plots of 20 m × 20 m were randomly laid in the forest reserve. Diameter at breast height, total height, crown diameter and wood density were measured. Forty quadrants of 1 m × 1 m for litter fall collection were also randomly laid in four locations in each permanent sample plots. Twenty four tree species present in all the permanent sample plots were selected for destructive sampling. Mean biomass of each sampled plots were pooled together to develop allometric equations to obtain biomass and carbons were also estimated using standard method. A total of nine hundred and forty seven tree species were measured in the study area. These tree species belong to sixteen different families. Allometric equations of family level and whole stand level for estimating above-ground tree biomass were therefore developed. The best fitted allometric equations were used to predict above-ground tree biomass. Model 3 indicated the highest modelling efficiency of 0.954, 0.960 and 0.984. Therefore taking this into consideration, that model 3 was selected as the best model for predicting the above-ground tree biomass with an estimation of 17698.76 g at family level. Allometric equations of whole stand level for above-ground tree biomass indicated good correlation with H, DBH, CD and WD (0.534, 0.597, 0.751, and 0.648). Model 5, 7 and 8 were designated the highest modelling efficiency of 0.898, 0.922 and 0.948. Model 8 is selected as the best models for predicting the above-ground tree biomass with an estimate of 838036.15 g. Therefore, carbon capture per hectare of above-ground tree biomass was 368280.40 g/ha. Carbon capture per hectare of litter had 2663.259 g/ha using standard method. The distributions of the standard residual values and standard error estimate with the fitted values are adequate.
<Keywords: Secondary forest; Biomass; Allometric equations; Carbon; Above-ground
General background
The cycling of carbon in forest ecosystems is a topic of considerable importance with rising atmospheric CO2 concentrations, global climate change, and the poorly defined role that terrestrial ecosystems play in mitigating or exacerbating these phenomena. In addition, increasing value is being placed on ecosystem services in forests; carbon cycling is among the most important of these services. The amount of organic matter in living and dead plant material is a critical component of the carbon cycle in forest ecosystems, providing both short and long term carbon sequestrations. Tropical forests, in particular, are major components of the terrestrial carbon cycle, accounting for 26 per cent of global carbon storage in biomass and soils [1-3].
The most accurate method for the estimation of biomass is through cutting of trees and weighing of their parts. This destructive method is often used to validate other, less invasive and costly methods, such as the estimation of carbon stock using non-destructive in-situ measurements and remote sensing [4,5]. Climate change is a product of greenhouse gas (GHG) Emission associated with the provision of energy services causing the current global warming [6]. Gases that contribute to the greenhouse effect are: water vapour, carbon dioxide (CO2), methane (CH4), and chlorofluorocarbons (CFCs) [7]. The emission of gases is a product of natural processes such volcanic eruptions but mainly by human activities, including deforestation, land use changes, burning fossil fuels, and agricultural like soil cultivation practices.
In the Global Forest Resource Assessment of FAO (2010) [8], it is estimated that all carbon stored in above-ground biomass, litter and soil of the entire world forests is around 652 billion tons with average carbon content of 161.8 tons per hectare. The Intergovernmental Panel on Climate Change (IPCC) estimates that at least one-third of the world’s remaining forests may be adversely affected by changing climate, especially in the boreal zone where the warming will be greatest. The Hadley Centre for Climate Change at the UK Meteorological Office has predicted that by 2050 forests globally will become a significant net source of CO2 emissions. Climate change impacts on biodiversity are already evidenced by shifting migration ranges of insects and animals, modified flowering and fruiting cycles, and species extinctions.
Over the years, several efforts have been made using different methods to estimate above-ground tree biomass models with high accuracy to extract reliable tree information [9]. Despite this, there are still considerable uncertainties in terms of accurate delineation of trees and methods that can standardize the estimations [10]. It is difficult to calculate the amount of carbon dioxide sequestered per tree per year due to the complexity of the major carbon pools involved, as well as the lack of research journals on tropical tree species. As forests safeguard carbon in biomass, the capacity of forests to serve as a practical means of removing excess carbon from the atmosphere is highly relevant today Nevertheless, the amount of carbon being sequestered annually is uncertain because of an absence of data and difficulties in measuring sequestration [11]. The broad objective of this study is to developed above-ground tree biomass models using forest volume and to estimate carbon stocks from the two pools in the study area.
The study area
The core area of International Institute of Tropical Agriculture (IITA) forest reserve lies at 07°30’ N and 03°55’E and about 227 m altitude in the city of Ibadan. The topography of the secondary forest area is undulating and gently slopes in the West-East direction with a well-drained soil thereby conditioning the soil of the forest to be well drained with large stones and gravel in several places which are conspicuous along parts of the short loop of the forest trail. The climate of the IITA forest is characterized by dry and rainy seasons. The dry season starts from early November and ends in the early part of the month of March. The rainy season follows, starting from late March and ending in early November, reaching its peak between June and September. The mean annual rainfall is about 1301.6 mm with average monthly rainfall being lowest in January (3-4 mm) and highest in June (189.7 mm) and September (217.9 mm), based on IITA meteorological data for a 20 year period (2000) (Figure 1).
Determination of biomass and carbon stock in the study area
Reconnaissance survey was first undertaken in the study area to obtain preliminary first- hand information of the situation in the forest reserve.
Laying of sample plots, transects and quadrants
Forest inventory based approach was adopted to estimate above-ground tree biomass in the study areas. Ten (10) 20 m x 20 m sample plots were randomly laid in the forest reserve. All the trees in each sample plot were labeled with the use of paper tape and marker in order to avoid leaving out any tree and also for easy identification.
Forty (40) 1 m × 1 m quadrants were also randomly laid in four (4) different strategic locations in each of the permanent sample plots so as to collect litter fall on the forest floor. The trees within a permanent sample plot were measured for diameter at breast height (DBH), diameter at middle, diameter at top, total height and crown diameter. The mean diameter at breast height (DBH) of all the trees within a permanent sample plot was calculated and the tree that had its diameter at breast height (DBH) closest to the mean diameter at breast height (DBH) was selected for destructive sampling so as to estimate its above-ground tree biomass.
Measurement of total height
This is the vertical distance between the ground level and the tip of a tree. It is obtained by taking the reading at the top (RT) and reading at the base (RB) which is usually negative (when on an elevated ground) and positive (when in a depressed ground or valley). It was measured with the aid of Spiegel Relaskop. The formula used to obtain the total height (H) using the metric scale is:
HT = RT-RB (1)
Where: H=Height
RT=Reading at the top, RB=Reading at the base
Measurement of tree diameter at Breast height (DBH)
This is the diameter measurement taking for a standing tree at height 1.30 m above the ground level. This tree parameter was taken for trees within the permanent sample plots. This measurement is generally accepted in forest inventory. It is the easiest measurable parameter in forest inventory with high degree of accuracy where guiding rules are followed. It was measured with the aid of diameter tape and has a unit of centimeter (cm).
Diameter at middle (Dm) and Diameter at the top (Dt)
These are diameter measurements made at various positions on the standing tree. Dm and Dt are measured with the use of Spiegel relaskop. Readings for Dm and Dt were taken in terms of numbers of bands of the relaskop occupied by the stem of the trees both at the middle and the top. These bands of relaskop are of two types, dark bands which are one unit each and big white bands which are four units each. The readings were taken by standing at a specified distance from the tree whose diameter is to be measured. The diameter was then calculated as:
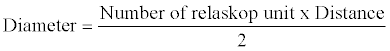 (2)
(2)
Measurement of crown diameter
Crown measurement was based on the assumption that the vertical projection of a tree crown is circular. Four (4) radii were measured along four (4) axes at right angle. Along the widest part of the tree crown, the tape was held horizontally and extended until each person is vertically under the tip of the longest branch on their side. Measurement was recorded as maximum width. The tape was then turned by 90° and measurement was repeated along the thinnest part of the tree crown and recorded as minimum width. Average crown diameter (Cd) was calculated by summing up the four radii and dividing by 2, thus:
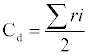 (3)
(3)
Where; Cd = average crown diameter, ri = projected crown radii measured on four axes.
Estimation of fresh weight of samples
Twenty four tree species present in all the permanent sample plots were selected for destructive sampling with the aid of chain saw. The felled tree species were partitioned into two components; the trunk and branches excluding the leaves. Five or more points along the tree trunk and branches of the tree species were marked. A wood disc of 3 cm thickness was obtained from each marked point to facilitate easy weighing at the laboratory in order to determine the fresh weight of the wood disc. The fresh weights of the litter fall were likewise obtained with the use of sensitive weighing balance.
Air-drying of samples
Samples of wood disc were taken to the screen house to air-dry for four weeks. Samples of litter fall were also taken to the screen house to air-dry for four weeks. The dry weights of the samples of the components were taken at the end of the four weeks.
Oven-drying of samples
Initial weights of the wood disc representing both the heartwood and sapwood regions was determined on a sensitive weighing balance and the wood disc were then oven-dried for 90°C to a constant weight for five (5) days.
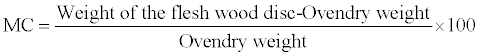 (4)
(4)
Where,
MC = Moisture content
Density estimation
Wood density of the appropriate tree components (wood disc) were obtained with the follow formula,
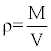 (5)
(5)
The average volumes of the wood disc length were determined while the areas of the wood disc were computed with the aid of LI-3100C Area Meter.
V=L×A (6)
Where;
ρ = density (g m-3), M = mass (g), V = volume (m3), L = length (m), A = Area (m2).
Allometric Equations
The general form of the allometric equation is
Y=αxβ (7)
Where;
Y = measure/process in equation, viz above-ground tree biomass, X = is size (usually DBH), β is the allometric exponent (which tells about the relationship between X and Y, α = constant, that is the allometric coefficient).
Allometric equations that were used to estimate above-ground tree biomass is as follows;
Model 1: AGTB = α (DBH)β (8)
Model 2: In(AGTB) = c + αIn(DBH) (9)
Model 3: In(AGTB) = c + αIn(DBH) + βIn(H) (10)
Model 4: In(AGTB) = c + αIn(H) (11)
Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) (12)
Model 6: In(AGTB) = c + αIn(DBH) + βIn(CD) (13)
Model 7: In(AGTB) = c + αIn(DBH) + βIn(WD) +ᵪln(H) (14)
Model 8: In(AGTB) = c + αIn(DBH) + βIn(avg WD) (15)
The values c, α, β and χ are best fit parameters.
Estimation of Carbon for the Study Area
The mean plot biomass for each species in the study area was calculated and then multiplied by 25 (the number of 20 m x 20 m plots in a hectare) to obtain the biomass per hectare. Half of the value gave the carbon stock per hectare for the location
Statistical analyses
Basal area estimation: The diameter at breast height (DBH) was used to compute basal area using the formula:
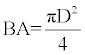 (16)
(16)
Where BA = Basal area (m2), π = 3.142, D = Diameter
Volume Estimation
Volume of each tree was estimated using Newton’s formula
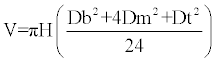 (17)
(17)
Where V = Stem volume (m3), H = total height (m), DBH = Diameter at breast height (cm), Dm = Diameter at the middle (cm), Dt = Diameter at the top (cm).
Tree species distribution
A total of nine hundred and forty seven (947) tree species were measured in the study area. These species belong to sixteen (16) different families as shown in tables 1 and 2.
| N/S | Species | Family | Frequency | % |
|---|---|---|---|---|
| 1 | Albiziazygia | Leg-Min. | 6 | 0.6 |
| 2 | Alchornealaxiflora | Euphorbiaceae | 4 | 0.4 |
| 3 | Antiarisafricana | Moraceae | 43 | 4.5 |
| 4 | Blighiasapida | Sapindaceae | 148 | 15.6 |
| 5 | Bombaxbuonopozense | Bombacaceae | 2 | 0.2 |
| 6 | Celtisafricana | Ulmaceae | 17 | 1.8 |
| 7 | Celtiszenkeri | Ulmaceae | 3 | 0.3 |
| 8 | Chrysophyllumalbidum | Sapotaceae | 54 | 5.7 |
| 9 | Dialiumguineense | Leg-Caes. | 10 | 1.1 |
| 10 | Ficusexasperata | Moraceae | 78 | 8.2 |
| 11 | Ficusmucuso | Moraceae | 2 | 0.2 |
| 12 | Funtumiaelastica | Apocynaceae | 139 | 14.7 |
| 13 | Holarrhena floribunda | Apocynaceae | 4 | 0.4 |
| 14 | Lecaniodiscuscupanioides | Sapindaceae | 40 | 4.2 |
| 15 | Massulariaacuminata | Rubiaceae | 81 | 8.6 |
| 16 | Morusmesozygia | Moraceae | 16 | 1.7 |
| 17 | Napoleonaeaimperialis | Lecythidaceae | 3 | 0.3 |
| 18 | Naucleadiderrichii | Rubiaceae | 45 | 4.8 |
| 19 | Newbouldialeavis | Bignoniaceae | 193 | 20.4 |
| 20 | Pycnanthusangolensis | Myristicaceae | 4 | 0.4 |
| 21 | Spondiasmombin | Anacardiaceae | 24 | 2.5 |
| 22 | Trichiliamonadelpha | Meliaceae | 20 | 2.1 |
| 23 | Trilepisiummadagascariense | Moraceae | 8 | 0.8 |
| 24 | Triplochitonscleroxylon | Sterculiaceae | 3 | 0.3 |
| Total | 947 | 100 |
Table 1: Data distribution according to tree species, family, frequency and percentage. Source: Fieldwork, 2013.
| S/N | Family | No. of tree species | No. of observations | % of the total |
|---|---|---|---|---|
| 1 | Anacardiaceae | 1 | 24 | 2.5 |
| 2 | Apocynaceae | 2 | 143 | 15.1 |
| 3 | Bignoniaceae | 1 | 193 | 20.4 |
| 4 | Bombacaceae | 1 | 2 | 0.2 |
| 5 | Euphorbiaceae | 1 | 4 | 0.4 |
| 6 | Lecythidaceae | 1 | 3 | 0.3 |
| 7 | Leg-Caes. | 1 | 10 | 1.1 |
| 8 | Leg-Min. | 1 | 6 | 0.6 |
| 9 | Meliaceae | 1 | 20 | 2.1 |
| 10 | Moraceae | 5 | 147 | 15.5 |
| 11 | Myristicaceae | 1 | 4 | 0.4 |
| 12 | Rubiaceae | 2 | 126 | 13.3 |
| 13 | Sapindaceae | 2 | 188 | 19.9 |
| 14 | Sapotaceae | 1 | 54 | 5.7 |
| 15 | Sterculiaceae | 1 | 3 | 0.3 |
| 16 | Ulmaceae | 2 | 20 | 2.1 |
| Total | 24 | 947 | 100 |
Table 2: Data distribution according to family, number of tree species and total number of occurrence in percentage.
Source: Fieldwork, 2013
Search of variables for estimating above-ground tree biomass
Scatter plots were devised for IITA secondary forest tree species to determine which of the four biometric parameters showed a strong relationship with above-ground tree biomass (AGTB) (Figure 2A-2D). The plots shows a clear non-linear relationship for DBH vs. AGTB, THT vs. AGTB, and a similar curve but with more scatter for CD vs. AGTB, with no clear relationship for WD vs. AGTB. The best predictor of AGTB in simple regression model will therefore be DBH. Natural logarithm, linear, cubic, quadratic, and power curves were fitted to DBH vs. AGTB data for IITA secondary forest tree species, restraining the intercept to zero (Figure 3).
The best fit was obtained from a natural logarithm, yielding an r2 value of 0.6320:
AGTB = α (DBH)β……………………………………………...........……….(Model 1)
The tree species become relatively top heavy as it grows, which is similar to changing the shape of a cone to a more cylindrical form. If the shape did not change, the volume (and weight) would increase as the square of the tree diameter. Plotting AGTB against the natural logarithmic term provided a perfect linearized relationship (Figure 3A and 3B) which can be more easily regressed and evaluated.
Allometric equations at family level
The regression coefficients, indicators of accuracy and significance are shown in table 3 for all models applied to the family of Bignoniaceae.
| Regression model | Coefficient symbol | Coefficient value | Standard error | r2 | Significance level of t-value |
|---|---|---|---|---|---|
| Model 1: AGTB = α (DBH) β | α β |
-0.015 0.002 |
0.002 0.000 |
0.632 | <0.0001 <0.0001 |
| Model 2: In(AGTB) = c + αIn(DBH) | c | -11.823 | 0.299 | 0.693 | <0.0001 |
| α | 2.314 | 0.111 | <0.0001 | ||
| Model 3:In(AGTB) = c + αIn(DBH) + βIn(H) | c | -11.701 | 0.276 | 0.743 | <0.0001 |
| α | 1.554 | 0.161 | <0.0001 | ||
| β | 1.282 | 0.210 | <0.0001 | ||
| Model 4: In(AGTB) = c + αIn(H) | c | -9.913 | 0.248 | 0.618 | <0.0001 |
| α | 2.851 | 0.162 | <0.0001 | ||
| Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | c | -11.823 | 0.299 | 0.693 | <0.0001 |
| α | 2.314 | 0.111 | <0.0001 | ||
| β | - | - | - | ||
| Model 6: In(AGTB) = c + αIn(DBH) + βIn(CD) | c | -11.716 | 0.322 | 0.694 | <0.0001 |
| α | 2.241 | 0.137 | <0.0001 | ||
| β | 0.128 | 0.139 | NS (0.9) |
Table 3: Regression models for estimation of above-ground tree biomass (AGTB) of 193 tree species of Bignoniaceae from secondary forest of IITA.
Source: Fieldwork, 2013.
Model 1 did not obey one of the assumptions of a linear regression. Variance of the distribution of the dependent variable should be constant for all values of the independent variable (Figure 3A). An In-In transformation of Model 2 (Figure 3B) makes the data cluster perfectly along the regression line. A further advantage of using this transformation is the property of logarithms, ln (xα) = α ln(x), which allows simplification of the exponent to unit value:
In (AGTB) = c + α In (DBH) ………………………………………………...….. (Model 2)
With the simple linear regression of model 2, the single independent variable ln (DBH) reduces the sum-of-squares variation of ln (AGTB) by 69.3%. Yet the estimates of AGTB for individual trees still diverge from the observed values. A modest improvement might be found by adding a second biometric predictor which accounts for differences in weight between trees of similar diameter. Adding total height (H) as a separate independent variable gives:
In (AGTB) = c + α In (DBH) + βIn(H) …………………...….……………….....(Model 3)
R2 increased slightly for the estimate of ln (AGTB) when a second independent variable was added to the best single independent variables, the result was always R2 ≥ r2. Since r2 was already high for the single variable model, standard error between observed and expected value of AGTB provides a more useful indictor of improvement. The t-value for the coefficient of H was significant at the p<0.0001 levels, however, and the standard error of 0.2758, 0.1612 and 0.2821 is large relative to the coefficient value of -11.7017, 1.5545 and 1.2821 (Table 3).
When correlation between two independent variables is high, multi-collinearity imposes itself on a multiple linear regression model, causing estimated partial regression coefficient for one or both independent variable to become less precise (t-values becomes less significant). This can occur even when both variables are very good predictors of the dependent variables. Total height (H) by itself is a fair predictor of above-ground tree biomass (r2 = 0.618; t-value of coefficient significant at the p<0.0001 level; see model 4 in Table 3, the lower confidence in its estimated coefficient in a multiple regression is a consequence of the high correlation between H and DBH. The correlation between these two variables is 0.74 for Bignoniaceae. For some other species, the correlation between H and DBH exceeded 0.80, forcing the use of a regression model with a single coefficient, derived from model 3 (see equation 4):
In (AGTB) = c + α In (DBH H).....………………………………………..... (Model 3A)
This simple model based on H alone has the form:
In (AGTB) = c + α In (H).....………………………………………….……… (Model 4)
Rotting or partially hollowed tree will have lower wood density causing lower AGTB. Its value as a predictor of AGTB was therefore tested.
If DBH and H are held constant, the relationship between AGTB vs. WD and AGTB vs. CD is expected to be linear. For a two different variable case: AGTB = c + α (DBH) β (WD) and AGTB = c + α (DBH) β (CD). The In-In transformation is:
In (AGTB) = c + α In (DBH) + β In (WD) ……………………………….....……. (Model 5)
Applying the data for Bignoniaceae, at 95% confidence interval for the partial regression coefficient of the wood density (WD) and crown diameter (CD) term includes zero and the t - value for CD was not statistically significant (Table 3).
There was no correlation coefficient between WD and DBH while the correlation coefficient between CD and DBH was only 0.64 for Bignoniaceae, so this is clearly not due to multi-collinearity. Rather, it indicates that wood density has no adequate values for predicting above-ground tree biomass, in the case of the 193 Bignoniaceae species studied.
In (AGTB) = c + α In (DBH) + β In (CD) ……………………………………...….. (Model 6)
Models 2, 3, 5, and 6 were applied to the other families of trees. Model 1 was excluded as it does not obey the assumption of a linear regression. Model 4 was excluded because of the very high average deviation between observed and predicted values of above-ground tree biomass for Bignoniaceae.
Model 3A was added when correlation between H and DBH did not permit statistically significant estimates of both partial regression coefficient using model 3 (i.e. when p>0.01). The other results on family allometric equations are given in Table 4 - 8.
| Regression model | Coefficient symbol | Coefficient value | Standard error | r2 | Significance level of t-value |
|---|---|---|---|---|---|
| Model 2: In(AGTB) = c + αIn(DBH) | c | -10.556 | 0.432 | 0.616 | <0.0001 |
| α | 2.478 | 0.143 | <0.0001 | ||
| Model 3:In(AGTB) = c + αIn(DBH) + βIn(H) | c | -10.874 | 0.425 | 0.645 | <0.0001 |
| α | 1.811 | 0.222 | <0.0001 | ||
| β | 1.253 | 0.327 | <0.0001 | ||
| Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | c | -9.496 | 0.264 | 0.865 | <0.0001 |
| α | 2.393 | 0.085 | <0.0001 | ||
| β | 0.926 | 0.050 | <0.0001 | ||
| Model 6: In(AGTB) = c + αIn(DBH) + βIn(CD) | c | -10.831 | 0.449 | 0.625 | <0.0001 |
| α | 2.726 | 0.187 | <0.0001 | ||
| β | -0.427 | 0.208 | <0.04 |
Table 4: Regression models for estimation of above-ground tree biomass of 188 tree species of Sapindaceae from the secondary forest of IITA.
| Regression model | Coefficient symbol | Coefficient value | Standard error | r2 | Significance level of t-value |
|---|---|---|---|---|---|
| Model 2: In(AGTB) = c + αIn(DBH) | c | -10.279 | 0.242 | 0.933 | <0.0001 |
| α | 2.410 | 0.077 | <0.0001 | ||
| Model 3:In(AGTB) = c + αIn(DBH) + βIn(H) | c | -10.512 | 0.207 | 0.907 | <0.0001 |
| α | 1.659 | 0.119 | <0.0001 | ||
| β | 1.332 | 0.176 | <0.0001 | ||
| Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | c | -9.938 | 0.346 | 0.872 | <0.0001 |
| α | 2.428 | 0.078 | <0.0001 | ||
| β | 0.490 | 0.358 | NS (0.2) | ||
| Model 6: In(AGTB) = c + αIn(DBH) + βIn(CD) | c | -10.373 | 0.259 | 0.933 | <0.0001 |
| α | 2.479 | 0.104 | <0.0001 | ||
| β | -0.118 | 0.117 | NS (0.3) |
Table 5: Regression models for estimation of above-ground tree biomass of 147 tree species of Moraceae from the secondary forest of IITA.
| Regression model | Coefficient symbol | Coefficient value | Standard error | r2 | Significance level of t-value |
|---|---|---|---|---|---|
| Model 2: In(AGTB) = c + αIn(DBH) | c | -10.789 | 0.253 | 0.887 | <0.0001 |
| α | 2.505 | 0.075 | <0.0001 | ||
| Model 3:In(AGTB) = c + αIn(DBH) + βIn(H) | c | -10.996 | 0.226 | 0.912 | <0.0001 |
| α | 1.974 | 0.107 | <0.0001 | ||
| β | 0.987 | 0.156 | <0.0001 | ||
| Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | c | -8.771 | 1.950 | 0.942 | <0.0001 |
| α | 2.497 | 0.076 | <0.0001 | ||
| β | 2.243 | 2.149 | NS (0.3) | ||
| Model 6: In(AGTB) = c + αIn(DBH) + βIn(CD) | c | -10.774 | 0.271 | 0.886 | <0.0001 |
| α | 2.493 | 0.107 | <0.0001 | ||
| β | 0.021 | 0.131 | NS (0.8) |
Table 6: Regression models for estimation of above-ground tree biomass of 143 tree species of Apocynaceae from secondary forest of IITA.
| Regression model | Coefficient symbol | Coefficient value | Standard error | r2 | Significance level of t-value |
|---|---|---|---|---|---|
| Model 2: In(AGTB) = c + αIn(DBH) | c | -12.591 | 0.626 | 0.522 | <0.0001 |
| α | 2.964 | 0.255 | <0.0001 | ||
| Model 3:In(AGTB) = c + αIn(DBH) + βIn(H) | c | -13.051 | 0.522 | 0.675 | <0.0001 |
| α | 1.387 | 0.296 | <0.0001 | ||
| β | 3.037 | 0.400 | <0.0001 | ||
| Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | c | -9.246 | 0.370 | 0.874 | <0.0001 |
| α | 2.397 | 0.135 | <0.0001 | ||
| β | 1.298 | 0.070 | <0.0001 | ||
| Model 6: In(AGTB) = c + αIn(DBH) + βIn(CD) | c | -13.046 | 0.569 | 0.617 | <0.0001 |
| α | 3.541 | 0.252 | <0.0001 | ||
| β | -1.202 | 0.218 | <0.0001 |
Table 7: Regression models for estimation of above-ground tree biomass of 126 tree species of Rubiaceae from secondary forest of IITA.
| Regression model | Coefficient symbol | Coefficient value | Standard error | r2 | Significance level of t-value |
|---|---|---|---|---|---|
| Model 2: In(AGTB) = c + αIn(DBH) | c | -10.572 | 0.263 | 0.945 | <0.0001 |
| α | 2.518 | 0.084 | <0.0001 | ||
| Model 3:In(AGTB) = c + αIn(DBH) + βIn(H) | c | -10.691 | 0.246 | 0.954 | <0.0001 |
| α | 1.977 | 0.187 | <0.0001 | ||
| β | 0.957 | 0.302 | <0.003 | ||
| Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | c | -10.572 | 0.263 | 0.945 | <0.0001 |
| α | 2.518 | 0.084 | <0.0001 | ||
| β | - | - | - | ||
| Model 6: In(AGTB) = c + αIn(DBH) + βIn(CD) | c | -10.608 | 0.264 | 0.946 | <0.0001 |
| α | 2.650 | 0.137 | <0.0001 | ||
| β | -0.292 | 0.240 | NS (0.2) |
Table 8: Regression models for estimation of above-ground tree biomass of 54 tree species of Sapotaceae from secondary forest of IITA.
Allometric equation at whole stand Level
The developed allometric equations at family level are very useful in IITA Forest Reserve. In other part of Nigeria however, different families of trees dominate regrowth forests. Thus, a set of whole stand equations were developed. These are based on the entire nine hundred and forty seven (947) tree species measured from twenty four (24) tree species of this study. This equation should be applicable to any species with growth from and joint ranges of DBH, H, WD, and CD similar to those of the trees in this study. Table 9 shows the result for four models developed above (models 2, 3, 5, and 6) plus two new models of the form:
| Regression model | Coeffecient symbol | Coeffecient value | SE | r2 | Significance level of t-value |
|---|---|---|---|---|---|
| Model 2: In(AGTB) = c + αIn(DBH) | c | -11.857 | 0.158 | 0.745 | <0.0001 |
| α | 2.768 | 0.053 | <0.0001 | ||
| Model 3: In(AGTB) = c + αIn(DBH) + βIn(H) | c | -11.922 | 0.141 | 0.799 | <0.0001 |
| α | 1.650 | 0.084 | <0.0001 | ||
| β | 1.905 | 0.120 | <0.0001 | ||
| Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | c | -9.661 | 0.116 | 0.898 | <0.0001 |
| α | 2.458 | 0.034 | <0.0001 | ||
| β | 1.057 | 0.028 | <0.0001 | ||
| Model 6: In(AGTB) = c + αIn(DBH) + βIn(CD) | c | -11.905 | 0.167 | 0.745 | <0.0001 |
| α | 2.811 | 0.070 | <0.0001 | ||
| β | -0.077 | 0.083 | NS (0.4) | ||
| Model 7: In(AGTB) = c + αIn(DBH) + βIn(WD) + χln(H) | c | -9.890 | 0.102 | 0.922 | <0.0001 |
| α | 1.731 | 0.053 | <.0001 | ||
| β | 0.968 | 0.025 | <.0001 | ||
| χ | 1.284 | 0.076 | <.0001 | ||
| Model 8: In(AGTB) = c + αIn(DBH) + βIn(avgWD) | c | -9.661 | 0.116 | 0.948 | <.0001 |
| α | 2.458 | 0.034 | <.0001 | ||
| β | 1.057 | 0.028 | <.0001 |
Table 9: Regression models for estimation of above-ground tree biomass (AGTB) for 947 tree species of sixteen families from secondary forest of IITA.
In (AGTB) = c + α In (DBH) + β In (WD) + ᵪ ln (H) ……………....……...………... (Model 7)
In (AGTB) = c + α In (DBH) + β In (avg WD) ………………………………..……..(Model 8)
Where ‘avg WD’ = the average wood density of trunk with bark for a given species.
Distribution of the standard residuals and R2 values for allometric equations at family level did not show a significant difference between model 5 and 6. The 3rd model indicated the highest modeling efficiency of 0.954, 0.960 and 0.984. Therefore taking this into consideration, that model 3 was selected as the best model for predicting the above-ground tree biomass (AGTB) with an estimation of 17698.76 g of the selected secondary forest reserve. Frequency distributions of the standard residuals with normal curves of that model were adequate.
Allometric equations at whole stand level indicated good correlation of AGTB with all the biometric parameters (Table 13). However, the distribution of wood density did not show a good correlation with total height, diameter at breast height and crown diameter (Table 13). The reason could be due to the poor management practices related to carbon estimation in the selected secondary Forest Reserve.
| S/N | Tree sp. | Family | Best Fitted Allometric Equation | AGTB (g) |
|---|---|---|---|---|
| 1 | 193 | Bignoniaceae | Model 3: In(AGTB) = c + αIn(DBH) + βIn(H) | 170793.00 |
| 2 | 188 | Sapindaceae | Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | 166368.30 |
| 3 | 147 | Moraceae | Model 2: In(AGTB) = c + αIn(DBH) | 130085.90 |
| 4 | 143 | Apocynaceae | Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | 126546.10 |
| 5 | 126 | Rubiaceae | Model 5: In(AGTB) = c + αIn(DBH) + βIn(WD) | 111502.20 |
| 6 | 54 | Sapotaceae | Model 3: In(AGTB) = c + αIn(DBH) + βIn(H) | 47786.64 |
| 7 | 24 | Anacardiaceae | Model 3: In(AGTB) = c + αIn(DBH) + βIn(H) | 21238.51 |
| 8 | 20 | Meliaceae | Model 3: In(AGTB) = c + αIn(DBH) + βIn(H) | 17597.74 |
| 9 | 20 | Ulmaceae | Model 3: In(AGTB) = c + αIn(DBH) + βIn(H) | 17698.76 |
| 10 | 947 | Whole stand | Model 8: In(AGTB) = c + αIn(DBH) + βIn(avgWD) | 838036.15 |
Table 10: Predicted AGTB Accumulation at Whole Stand Level Using Allometric Equations.
| Plot | Mean plot biomass (g) | AGTB per ha (g) | Carbon per ha (g/ha) |
|---|---|---|---|
| 1 | 5387.51 | 134687.70 | 67343.85 |
| 2 | 3207.05 | 80176.20 | 40088.10 |
| 3 | 3014.83 | 75370.78 | 37685.39 |
| 4 | 3787.90 | 94697.45 | 47348.73 |
| 5 | 1221.96 | 30548.98 | 15274.49 |
| 6 | 3699.11 | 92477.68 | 46238.84 |
| 7 | 2907.47 | 72686.75 | 36343.38 |
| 8 | 2068.64 | 51715.98 | 25857.99 |
| 9 | 2814.37 | 70359.23 | 35179.61 |
| 10 | 1353.60 | 33840.08 | 16920.04 |
| Total | 368280.40 |
Table 11: Carbon Values of AGTB in the Study Location Using Standard Method. Source: Fieldwork, 2013.
| Plot | Mean plot biomass (g) | Litter Biomass per ha (g) | Carbon per ha (g/ha) |
|---|---|---|---|
| 1 | 28.234 | 705.850 | 352.925 |
| 2 | 32.592 | 814.801 | 407.400 |
| 3 | 17.354 | 433.841 | 216.920 |
| 4 | 13.764 | 344.084 | 172.042 |
| 5 | 31.470 | 786.753 | 393.377 |
| 6 | 21.495 | 537.369 | 268.684 |
| 7 | 17.543 | 438.575 | 219.288 |
| 8 | 14.718 | 367.954 | 183.977 |
| 9 | 17.622 | 440.560 | 220.280 |
| 10 | 18.269 | 456.732 | 228.366 |
| Total | 2663.259 |
Table 12: Carbon Values of Litter Fall in the Study Location by Using Standard Method. Source: Fieldwork, 2013.
| H | DBH | CD | DENSITY | AGTB | |
|---|---|---|---|---|---|
| H | 1.00000 | ||||
| DBH | 0.83251 <0.001 | 1.00000 | |||
| CD | 0.62396 < 0.0001 | 0.71514 < 0.0001 | 1.00000 | ||
| DENSITY | 0.21925 < 0.0001 | 0.15784 < 0.0001 | 0.14258 < 0.0001 | 1.00000 | |
| AGTB | 0.53360 < 0.0001 | 0.59656 < 0.0001 | 0.75144 < 0.0001 | 0.64753 < 0.0001 | 1.00000 |
Table 13: Pearson Correlation Coefficients, N = 947. (Prob. = <0.0001).
Clearly, inherent differences in forest stand form, degree of self-thinning and crown characteristics, necessitated the development at family and whole stand level relationships. Moreover, when tested, crown diameter became insignificant in the allometric equations (Table 9). Model 5, 7 and 8 (Table 9) designate the highest modeling efficiency of 0.898, 0.922 and 0.948. Therefore taking this into deliberation, that model 8 is selected as the best models for predicting the above-ground tree biomass with an estimation of 838036.15 g of the selected Forest Reserve. the carbon partitioning between major carbon pools estimated carbon capture per hectare of above-ground tree biomass to be 368280.40 g/ha and carbon capture per hectare of litter to be 2663.259 g/ha. The carbon values in the study location showed great variations across the PSP as these could due to invasion of lanais at the study site. The distributions of the standard residual values with the fitted values are adequate as these models proved the quality, reliability and suitability of selection for further analysis, so that the research findings can be extrapolated for managing forests related to carbon.
Evaluation of the selected models
For the purpose of testing the constructed models, both qualitative and quantitative tests (frequency distribution, standard residuals, normal curve, and coefficient of determination (R2) were used. The coefficient of determination (R2) on its own is not a very good indicator of the accuracy of a model. Standardized residual plots of fitted values do not give a quantitative result although they are useful indicators for bias. Therefore the necessity of some other tests to identify the model performance such as lack of fit is clearly highlighted. Furthermore, two forms of bias exist when using logarithmic transformations. Small variations in the biometric input from small trees can influence the slope and intercept of the linear regression coefficients more than large trees. Secondly, as evident in this study, an inherent curvature tends to underlie the model, even after log transformation [12]. Further refinement of the models developed in this study would require larger data sets.
Among the multiple methods for estimating above-ground biomass models, the permanent sample plots (PSP) method is covered in detail because it is simple, reliable, widely applicable and cost-effective. The critical components of the procedure are sampling and field measurement. The data gathered using the PSP method will enable estimation of above-ground tree biomass stock, growth rate and stock changes. Adoption of permanent plot methods will enable long-term and periodic measurement and estimation of carbon stocks over any selected period.
Allometric equation at family level provided good estimates of above-ground tree biomass models of IITA secondary forest trees. Wood density is an important driving variable when the whole stand equations were used (Table 9). For the estimation of AGTB models, the best approach is to apply whole stand regression equation which uses both diameter and average wood density as independent variables (Model 8). Wood density can be derived from a sample of trees for each species if they do not vary much with age. Adding total height as an additional input variable does not provide much improvement in the whole stand model. Total height should only be included as a driving variable if it is accurately measured and then probably only when using the family level models. Regression analysis of the residuals and the predictors revealed that no trend was observed, suggesting that the models were fair toward an over or under estimation of biomass for either small or larger trees.