Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Review Article - (2014) Volume 4, Issue 5
I explore the collision of localized structures that arise from a general initial solutions in the Peyrard- Bishop model. By means of the semi-discrete approximation, it is shown that the amplitudes of waves are described by the the discrete nonlinear Schrödinger equation. The corresponding soliton solutions of this equation are obtained through the Hirota’s bilinearization method. These solutions include the one- as well as the two-soliton solutions. Particular attention is paid to the behaviors displayed by the two-soliton solution. Taking one of the soliton as a pump and the other as the bubble that describes the local opening of the two strands of DNA, I show that, the enhancement of the bubbles is due to energy transfer from the pump to the bubble within the collision process. It is also shown that the underlying solitons undergo fascinating shape changing (intensity redistribution) collision.
<Keywords: PB model; DNLS equation; Hirota method; Discretesoliton; Collision
DNA dynamics continues to attract a great deals of interest nowadays. Its complex structure and dynamical features are on the basis of life at the molecular level. The interest in the nonlinear dynamics of DNA started when Englander et al. [1] suggested that the existence of solitons propagating along the DNA molecule may be important in a process called “DNA transcription”. In the last decade, several models were proposed in order to substantiate this idea in quantitative terms. The scope of RNA transcription is to copy genetic information from DNA into messenger RNA. During this process, the two DNA strands have to locally separate (local opening of DNA) to let the genetic information stored within one of the strands be copied into RNA polymerase that will be the template for the synthesis of the protein. There are two important models, the one proposed by Yakushevich [2] and improved by Gaeta [3], and the second proposed by Peyrard and Bishop (PB) [4] which concentrate on transversal openings of base pairs. In fact, the PB model is one of the simplest models that investigates DNA at the scale of a base pair [4]. The complex double-stranded molecule is described by postulating some simple effective interactions among the bases within a pair, and along the strands. The model has been successfully applied to analyze experiments on the melting of short DNA chains [5]. Furthermore, it allows to easily include the effect of heterogeneities [6] yielding a sharp staircase structure of the melting curve (number of open base pairs as a function of the temperature T) [7]. Beyond its original motivation to explain the denaturation, the PB model has an intrinsic theoretical interest as one of the simplest one-dimensional systems displaying a genuine phase transition [8,9].
The nonlinear effects might focus the vibration energy of DNA into localized soliton-like excitations [10-15]. Indeed, the local opening can be analytically described as breather-like objects of small amplitude, which have nevertheless interesting properties; as long as their amplitude is small enough they can move along the chain. Thus, comes out the importance of discrete solitons in explaining local openings of the hydrogen bonds and formation of denaturation bubbles. Discrete solitons in nonlinear lattices have been the focus of considerable attention in diverse branches of science [16-18] and they are possible in several physical settings, such as biological systems [19-23], atomic chains [24,25], solid state physics [26], electrical lattices [27] and Bose- Einstein condensates [28]. In DNA, such waves have been shown to carry the energy necessary for the initiation of the complex and key phenomena of replication and transcription [11-14]. In recent studies, on DNA models, the role of the enzymes such as RNA polymerase has been shown to be the collection of the thermal energy available in the system [13,15], an argument which has motivated the present work. The discrete character of DNA is exploited to show that such energy and the DNA bubble during transcription, for example, behave like shapechanging colliding discrete solitons. The problem is therefore solved in a pure discrete way, where the generic PB model is first reduced to a discrete nonlinear Schr¨odinger (DNLS) equation. Exact one- and two-soliton solutions for the latter are then investigated via the discrete Hirota method [29-32]. The rest of the paper is therefore structured as follows. In section“model and mathematical background”, after a brief presentation of the PB model of DNA dynamics, I sketch the discrete expansion method that allows me to obtain the equation that governs the amplitude of planar waves in the form of the DNLS equation. In section“Discrete Solitons Solution of the PB Model”, I present the one-soliton and two-soliton solutions obtained by the Hirota’s method. I study the collision of these solution in the PB model with DNA parameters by means of direct numerical experiments, using the solutions described above as initial conditions, in section “Soliton Interaction, Collision and Shape Changing in the PB Model”. I show that the underlying solitons undergo shape changing-intensity redistribution collision. The last section“conclusion”is devoted to concluding remarks and outlooks.
The PB model is one of the model describing the dynamics of largeamplitude localized excitations in the DNA molecule [4,33]. The B-form DNA in Watson-Crick model is a double helix, which consists of two strands, S1 and S2, linked by nearest-neighbor harmonic interactions along the chain. The strands are coupled to each other through hydrogen bonds, which are supposed to be responsible for transverse displacements of nucleotides. Only the transversal displacements of the bases, denoted byynand zn, from their equilibrium positions along the direction of the hydrogen bonds, are considered. The molecule consists of the following elements: a common mass mis used for all the nucleotides in a strand, and the same coupling constant k along each strand is assumed. Using the above notations, the Hamiltonian of the discrete system is written as follows [4,33]:
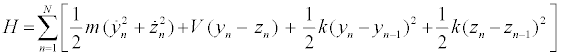 (1)
(1)
The intrapair potential is the Morse potential V (yn − zn) = D[e−a(yn −zn) − 1]2, where D is the dissociation energy and a a parameter homogeneous to the inverse of a length, which sets the spatial scale of the potential. The Hamiltonian (1) gives the equations of motion for yn and zn
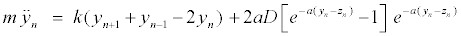 (2)
(2)
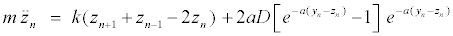 (3)
(3)
To analyze the motion of the two strands, it is convenient to introduce the following dependent variables,
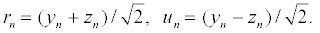 (4)
(4)
I then have
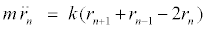 (5)
(5)
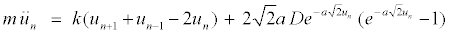 (6)
(6)
The variables rn and un represent the in-phase and out-of-phase elongations, respectively. Equation 5 is a linear differential-difference equation with the usual plane wave solutions whereas equation 6 contains nonlinear terms. It is interesting to relate our model to nonlinear excitations. The equations of the out-of-phase motion are then written, after expanding the terms in exponential, as
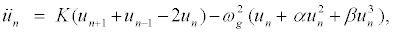 (7)
(7)
where
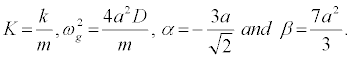 I use the parameter values D = 0:04eV (=0:64x10-20J), a = 4:45Å-1(= 4:45×10-10m-1), m = 300 a.m.u (= 5:00×10-25 Kg) and the coupling parameter k = 0:06eV/ Å2(= 0:96 J=m2),
I use the parameter values D = 0:04eV (=0:64x10-20J), a = 4:45Å-1(= 4:45×10-10m-1), m = 300 a.m.u (= 5:00×10-25 Kg) and the coupling parameter k = 0:06eV/ Å2(= 0:96 J=m2),
which have been widely used in DNA-like models [34,35]. Equation 7 is a nonlinear ODEs which cannot be solved exactly.
It is thus convenient to think about reducing equation 7 to a more simple system that, under some approximations, can allow us to find and study localized structures. In this sense, many techniques are nowadays used to derive DNLS equation from discrete differential equations. Some of them have been introduced: by Peyrard and Kivshar [36], by Daumont et al. [37] as well as recently by Johansson [38], just to name a few. In this work, we paid our attention to the one used by Johansson. The one used by Kivshar and Peyrard [36] can be extended here but, since the Morse potential is nonsymmetric, the method used by Daumontet al. [37] is appropriate. In fact, it takes into consideration the first harmonics and introduces a few functions Fj,n, which bring out the importance of nonlinear parameters. It amounts in considering the solution of the nonlinear equation in the form
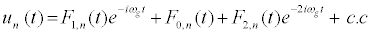 (8)
(8)
The subsequent system in terms of the harmonics eilωgt, with l = 0; 1; 2, are obtained as follows:
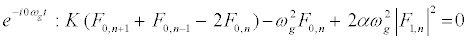 (9)
(9)
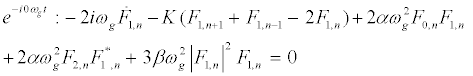 (10)
(10)
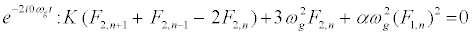 (11)
(11)
To extract the different harmonics, I assume that the envelopes are slowly varying, i.e., 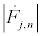
 , and consider a highly discrete lattice which implies
, and consider a highly discrete lattice which implies 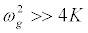 . On these hypotheses, equations (9) and (11) give the harmonic F0,n and F2,n in the form
. On these hypotheses, equations (9) and (11) give the harmonic F0,n and F2,n in the form
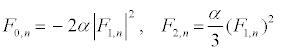 (12)
(12)
The above solutions are then replaced into equation 10 and one obtains the following one-dimensional modified discrete NLS equation:
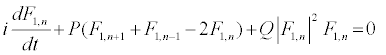 (13)
(13)
where P and Q are given by,
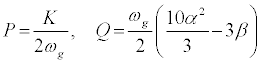 (14)
(14)
The NLS equation is among the most important physical models in the field of nonlinear waves. Be- sides its fundamental value as a first-order nonlinear wave equation, it is an integrable model in the one-dimensional case [25] and represents many different physical systems: from laser wave packets propagating in nonlinear material to matter waves in Bose-Einstein condensates, gravitational models for quantum mechanics, plasma physics, here DNA, or wave propagation in geological systems, among others [26-28]. In the next section “Discrete Solitons Solution of the PB Model”, I will apply the Hirota’sbilinearization method to check soliton like solutions of the DNLS equation 13 [38-40].
The construction of the exact solutions of nonlinear partial differential (NLPD) equations is one of the most important and essential tasks in nonlinear science. With the help of exact solutions, when they exist, the phenomena modelled by NLPD equations can be better understood. In recent decades, many powerful methods to construct exact analytical solutions have been proposed. Among them, we have the tanh-function method [41], the elliptic function approach [42], and the Hirota’sbilinearization method [29-32], to name just few. Here, the Hirota’sbilinearization method is used to investigate exact solitons solution of the PB model. In so doing, the Hirota bilinear transformation F1, n= gn/fn [29-32] is applied, where gn and fn are complex and real functions, respectively. Introducing the above transformation into equation 13 and decoupling the resultant equation lead to the bilinear equations
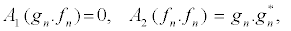 (15)
(15)
with
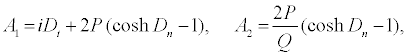 (16)
(16)
where the Hitota’s bilinear operators Dt and Dn are defined by:
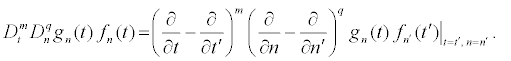 (17)
(17)
The above set of equations can be solved by introducing, for example, the following power series expansion for the functions fn and gn in powers of a small parameter ε as
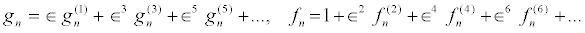 (18)
(18)
The bright one-soliton solution of the PB equation
In order to obtain the bright one-soliton solution of the DNLS equation 13, I assume
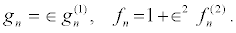 (19)
(19)
Then, inserting equation 19 into equation 16 and collecting terms of the same power in ε, I obtain
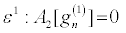 (20)
(20)
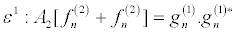 (21)
(21)
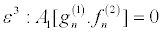 (22)
(22)
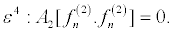 (23)
(23)
we set
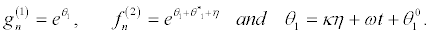 (24)
(24)
Equation 20 and equation 21 successively give
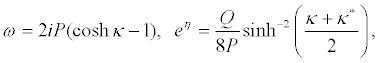 (25)
(25)
and I can write the solution of equation 13, taking ε = 1, as
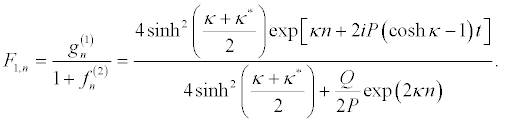 (26)
(26)
The above one-soliton solution is depicted in Figure 1.
The bright two-soliton solution of the PB equation
To obtain the bright two-soliton solution, the power series expansion are expressed at the higher-order terms
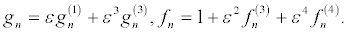 (27)
(27)
Then by solving the resultant linear partial differential equation recursively, the following expressions, in powers of ε,
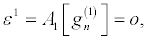 (28)
(28)
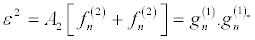 (29)
(29)
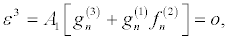 (30)
(30)
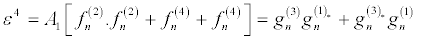 (31)
(31)
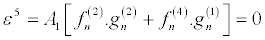 (32)
(32)
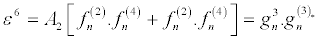 (33)
(33)
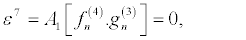 (34)
(34)
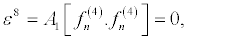 (35)
(35)
are obtained. By setting
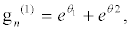 (36)
(36)
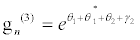 (37)
(37)
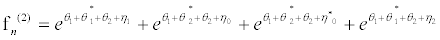 (38)
(38)
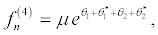 (39)
(39)
and
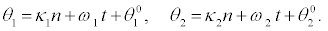 (40)
(40)
I substitute equations 36-39 into the set of equations 28-35 and equation 28 and equation 29 successively give
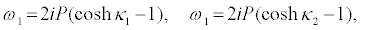 (41)
(41)
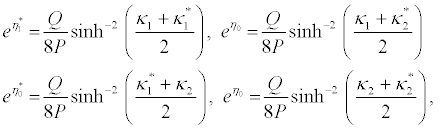 (42)
(42)
And equation 30 and equation 31 successively give
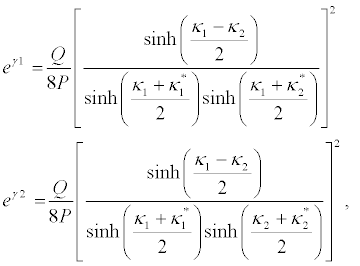 (43)
(43)
and
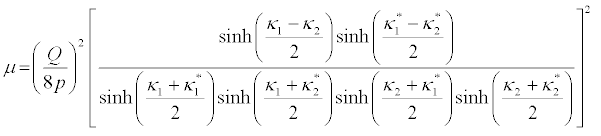 (44)
(44)
The solution of the DNLS equation, for ε = 1, is then written as
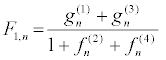 (45)
(45)
One of the most essential properties of solitons concerns their interaction and their behaviors at collisions [43]. Some striking differences exist in the nature of interactions between solitary waves in media with saturable nonlinearity with those of their well-known Kerrsoliton counterpart. As shown in ref. [44] for the (1+1) D case, solitons of the lower solution branch in media with saturable nonlinearity behave quasi elastically, similar to Kerr solitons, and retain their shape after collision. In contrast, two solitons of the upper solution branch with a saturable small crossing angle (or a small frequency shift in the case of temporal solitons) fuse to a single solitary output waves with a changed propagation direction. In this section “soliton interaction, collision and shape changing in the PB Model”, I investigate the elastic and inelastic collisions between two bright solitonsS1and S2 shown in figures 2-4.
In figure 2, for κ1 = 1.0 + i and κ2 = 1.5 − i, I have a pure elastic collision of the two solitons which are well separated before and after collision. This case is not really interesting for this work because, it does not explain the features observed in real DNA. Contrarily, in figures 3 and 4, I observe shape changing and intensity redistribution of the initial soliton. It is possible to design one of the solitons, either S1 or S2, as an energy reservoir (pump) and the other one as the transcription bubble (or the data carrier). This is depicted in figure 3, where S1 represents the bubble and S2, the energy pump, due to thermal fluctuations available in the molecule. In fact, the first step of the transcription of DNA is a local opening of the double helix that extends over about 20 base pairs. Such local unwindings of the helix can be obtained by heating DNA to about 70oC. But in the life of an organism they must occur at physiological temperature. This is achieved by the action of an enzyme. However, one may wonder how this can be possible since, whatever its origin, the local opening requires the breaking of the same number of hydrogen bonds, hence the same amount of energy, and the enzyme does not bring in energy. Of course, under normal physiological conditions there are thermal fluctuations along the DNA chain. They can be weakly localized by nonlinear effects to generate what biologists called “Breathing of DNA”. But their intensity is not high enough to open the double helix over many base pairs. A possible pathway to the opening would be to collect the thermal energy that is present along DNA and, this could be the role of the enzyme. In so doing, S2 can be described as the energy collected along DNA, which enhances the bubble S1 and tends to vanish. The same behaviors are observed in figure 3(b), where the role is changed. This is fully reinforced by the suppression of one of the initial solitons in figure 4. As one can see, the total energy collected is used to enhance either the bubble S1or the bubble S2 (Figure 4), while the pump completely disappears. We can conclude that, in all dynamical process (replication, transcription,...) which take place in DNA, there is a need of energy to occur and, this energy is brought by the molecule itself. In this frame, thermal fluctuations, which exist in the molecule at physiological temperature, are shown to be a pathway to energy localization and formation of local structures [45,46]. Furthermore, it has been shown recently by Kalosakaset al. [47,48] how a combination of these thermal fluctuations, sequence specificity, and nonlinearity induce large and slow bubbles in the chain that coincide with the localization of start site of transcription [47,48].
Studying nonlinear excitations in biopolymers still attracts deep interest. It contributes to describe biomolecular processes, such as the vibrational energy transport in proteins on the basis of 1D nonlinear lattices, the energy localization and the transcription and replication phenomenon in DNA. Many models have been proposed to account for these nonlinear phenomenon but, the one used in this work is the PB model. It is shown in this work that, the local openings of the complementary base pairs can be described by the DNLS equation. Using the Hirota method, I have derived the one- and two- solitons solution of the PB model. These solutions are well already known as the consequence of energy localization in DNA. The head-on collisions of these solutions have been explored. The exchanged energy results from the collision of two bubbles, causing the intensity and the width of one of the bubbles to change in some cases. The collision may be elastic, that is, the two bubbles keep their shape as before the collision, or inelastic, that is, there is energy exchange leading in some cases to the suppression of one of the soliton. The inelastic collisions can explain the enhancement of transcription bubbles. It is indeed known that, in such a process, there is collection of the available thermal energy, present in the molecule at physiological temperature, by enzymes. That energy is carried by one of the solitons which acts as the energy pump while the other solitons is the bubble itself which receive that energy. The interactions could lead to the suppression of the pump. Furthermore, the stability of such solitons has been shown thus, they are good candidates in describing transcription and replication of DNA. Such a study is not complete and should be taken with prudence in real DNA studies because, it does not take into account the conformational changes due to twisting and even the modelling of the vibrational phenomena present in DNA. In so doing, it will be of a great interest to perform such a study in a model where, helicity and thermal bath are taken into account.