Particulate matter (PM) refers to particles that are suspended in the atmosphere [1]. These particles are of different types and sizes (some being visible to the eye while some being microscopic). It is composed of both solids and liquids. Researchers’ interest in PM-related studies increased only in the 1980s with at least 1500 research papers being produced each year [2]. This is due to the effects that PM has to the quality of air, which in turn affects human health and the environment. PM is a pollutant of air [2,3].

PM of less than 10 microns (PM₁₀) refers to particles of diameter less than 10 μm [3]. PM_2.5 is referred to as fine PM. It (PM) includes particles with diameter less than 2.5 μm [3,4]. Fine PM, especially that with diameter less than 0.1 μm, can remain in the atmosphere for several days [1]. PM constitutes physical, chemical and biological particles [1]. These include, for example, products of combustion such as ashes, dust blown by wind, droplets of liquids, fragments of living things and extremely small living organisms, sulfates, nitrates and ammonium [3].

Where do these particles suspended in the atmosphere come from? The particles are introduced in the air through human activities and natural ways [2]. These particles are either directly emitted into the air (primary particles) or they are formed in the air through chemical reactions of gaseous pollutants (secondary particles) [1,3]. Some of the sources of primary particles are solid fuel combustion, combustion engines, agricultural activities, sea-salt spray, and industrial activities such as building, mining, manufacture of cement, ceramic and bricks, and smelting [1-3,5]. Other constituents of PM are formed in the atmosphere (through chemical reactions) from, for example, sulfur dioxide, oxides of nitrogen, ammonia and non-methane volatile organic compounds [1,2]. Other constituents of PM are extremely small living organisms, and fragments of living things [6].

PM air pollution has health effects which can be due to short-term or long-term exposure. Our respiratory system cannot filter out particles of less than 10 microns (PM₁₀) [1,3,7]. PM air pollution is likely to cause coughing, wheezing, and overall decreased lung function [3]. Thus it (PM air pollution) can lead to increase in hospital admissions which in turn results into a lot of resources being required for treatment. It can also lead to mortality from cardiovascular and respiratory diseases, and lung cancer [1]. PM air pollution makes susceptible groups such as the elderly, children, and those with pre-existing lung or heart disease vulnerable [1,3].

Apart from health effects, PM air pollution has environmental effects such as impaired visibility and acid decomposition [4,7]. Acid rain has effects on the water and land ecosystems. Thus acid rain is likely to endanger biodiversity. PM in the atmosphere is capable of absorbing and scattering solar radiation, hence influencing the climate [7]. Jimoda [7] further says PM also leads to global forcing.

Given times series (TS) of PM for different areas, there is a possibility that some of the areas may have their particulate matter TS behaving similarly. With the TS behaving similarly, we can cluster the locations. Clustering reduces costs of monitoring the locations. Instead of monitoring all the locations, representative areas can be selected from each cluster. Studies can also be carried out on selected locations which are a representative sample. The results can be applied to locations which have similar patterns as those in the sample. Scott et al. [8] applies, develops and compares two methods for clustering TS. The two methods are applied to Total Organic Carbon data from river sites in Scotland. One of the methods used involves viewing the TS under consideration as functional data and uses hierarchical clustering, and the second approach uses state-space model in clustering the TS [8]. Finazzi et al. [9] compares two approaches of clustering TS. One of the methods is a modification of the classic state-space modelling approach while the other method is based on functional clustering. Finazzi et al. [9] applies the two methods to lake surface water temperature for 256 lakes globally for the purpose of comparing their performance. For the functional approach of clustering, Finazzi et al. [9] uses both k-means and complete-linkage hierarchical clustering algorithms.

This paper intends to cluster TS of PM₁₀ for African countries. With the possibility that the levels of PM₁₀ might follow similar patterns for some countries, exploring clusters to which these countries are likely to belong based on the patterns that their TS of PM₁₀ follow is of significance (as indicated in the next paragraph). The TS data of PM₁₀ is somewhat not (very) recent (observations are from 1990 to 2006), hence 2014 Cross-sectional data of PM_2.5 for African countries will also be clustered.

Africa is poor (many countries in Africa are poor) [10]. It is a challenge to these countries to keep tract of all aspects related to PM air pollution. Clustering TS of PM₁₀ for these countries will ensure efficient and effective use of resources. When a PM-air-pollution-related study is to be conducted, instead of conducting the study on all the countries, representative sample countries can be selected from each cluster for the study. Monitoring of levels of PM can also be done only on representative sample countries. Countries can simply consider results obtained from another country in a given study related to PM air pollution without carrying out a similar full scale study.

The next section, Section 2, provides descriptions of the data sets that are considered in this paper. Section 3 looks at the tools that are employed in the analysis. In Section 4, tools described in Section 3 are used to carry out the analysis. Discussion of the results is done in Section 5. A general reection on the work is given in Section 6.

Data description

Data that are being considered in this paper, which are provided by United Nations Environment Programme [11], are levels of concentration of PM₁₀ in African countries in the period between 1990 and 2006. These are annual concentrations at national level (annual exposure levels of an average urban resident to outdoor PM). These concentration levels are obtained from residential areas of cities with more than 100,000 residents. They (concentration levels) are estimates obtained using the Global Model of Ambient Particulates (GMAPS). Each national concentration level is an average of concentration levels in the cities. The data (and the data set described below) are in μg/m³. There are 17 time points being considered. In the analysis, Cabo Verde, Seychelles and South Sudan are not considered because they do not have observations. We are considering 51 countries. Figure 1 gives the locations being considered.

Figure 1: Map of Africa: adapted from World Atlas [28].

The data from United Nations Environment Programme [11] are not (very) recent, hence in the analysis, we will also consider 2014 cross-sectional data of annual mean concentration levels of PM of less than 2.5 microns of diameter (PM_2.5) in urban areas (provided by World Health Organisation [12]). The observations are for Africa only. The data set does not have observations for Cabo Verde and Sao Tome. The observation for Seychelles has been removed (observations for this country are not available in the former data set) while that of South Sudan (there are no observations for this country in the other data set) will be used. The aim is to have the same number of countries in the two data sets in order to be able to check the extent to which clusters from the two data sets agree (method used requires so).

The data set has multiple TS. The focus is on clustering the TS as they are (without standardize the TS). Since TS will not be standardized, functional clustering is an appropriate approach for clustering [9]. Multiple TS will be represented in functional form, thus having an advantage of looking at the trajectories as a whole. Finazzi et al. [9] in comparing clustering algorithms, k-means and Completelinkage hierarchical, finds out that both algorithms produce almost the same results in clustering multiple TS. Complete-linkage hierarchical algorithm will be used to cluster the TS that will be in functional form. To determine the number of clusters, dendrogram (dendogram) will be used. Validation of the results will be done using Silhouette. The statistical package R (the libraries fda, cluster, RColorBrewer, rworldmap and clues) will be used in the analysis. The functions to be used are read.csv, nrow, ncol, rep, plot, lines, matrix, paste, par, abline, points, cbind, apply, data.frame, if, for, inprod, rainbow, create.bspline. basis, fdPar, smooth.basis, daisy, hclust, silhouette, cutree, brewer.pal, join CountryData2Map, mapCountryData and adjustedRand.

The data we have are TS of continuous data. The data can be approached as functional data [13]. Each TS can be written in functional form [13,14]. Thus

y_ij = x_i (t_ij) + ∈_ij  (1)

y_ij is the observation in the ith TS at time j; x_i(t_ij) is the observation in the ith smooth curve at time j; and ∈_ij is an independent random error for the ith curve at time j.

Each smooth curve x_i(t_i) is a linear combination of basis functions [13]. Thus

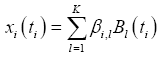(2)

βi is a vector of coefficients and B(t) = (B₁(t), B₂(t), …, B_K(t)) is a set of basis functions.

In smoothing the curves, the total curvature will be penalised. Generalised cross validation (GCV) will be used to choose the smoothing parameter. The interest is in the value of the smoothing parameter that minimizes the GCV (the value that minimizes the sum of predicted squared errors) [15].

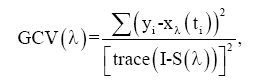(3)

where S is the smoothing matrix, and x_λ(t_i) are predicted values for a given value of λ.

Complete-linkage hierarchical algorithm

Complete-linkage hierarchical algorithm will be applied to the vectors of the coefficients βi as presented by Finazzi et al. [9] and Scott et al. [8]. By clustering the vectors of the coefficients, the corresponding TS will be clustered. In using this algorithm, there is no need to specify the number of clusters in advance [16,17]. The algorithm starts by assigning all elements to their own clusters. Then distances between the clusters are calculated. Clusters with smallest distance between are merged into one. The calculation of distances and the merging is done until there is only one cluster [18,19].

The distance between the ith and jth curves, whose vectors of coefficients are βi and βj

respectively, is given by

d_ij = (β_i - β_j)^TW (β_i - β_j)     (4)

where W = ∫ B(t) B(t)^T dt is a square matrix [8].

With complete linkage, the distance between two clusters is considered to be the maximum distance of distances of all possible pairs of elements from the two clusters (the elements of each pair are not from the same cluster) [15,16]. Thus the distance between clusters C₁ and C₂, with elements c1 and c2 respectively, is

D (C₁,C₂) = max {d(c₁,c₂) : c₁∈C₁, c₂∈C₂    (5)

Determining the number of clusters

To determine the number of clusters, the dendrogram will be used [20]. This is a tree structure that allows the visualisation of the structure of the data in terms of clustering (it allows the visualisation of the merging of clusters). It is used in making decision on the possible number of clusters available in the data. A large gap between joints far up in the tree provides an evidence that the procedure started merging clusters that are far apart (merging incorrectly).

Cross-sectional data (raw data) from World Health Organisation [12] will be clustered using complete-linkage hierarchical algorithm.

Cluster validation

To validate the clusters the Silhouette will be used. This is a graphical method that shows how well a member of a cluster fits in the cluster [21]. The silhouette ranges from -1 to 1, where a high value indicates that a member is well matched to its own cluster than neighboring clusters [21,22].

For a given cluster C_j with j = 1; : : :; k where k is the number of clusters, the Silhouette value of the ith sample of the cluster C_j is given by

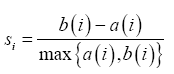(6)

where a(i) is the average distance between the ith and all samples in C_j and b(i) is the minimum average distance between ith sample of C_j and any other cluster to which ith sample is not a member [23,24].

Adjusted Rand Index (ARI) will be used to determine the agreement between clusters from the two data sets [25,26].

The data are TS of PM₁₀ for 51 African countries. There are 17 observations for each country. The observations are continuous. Figure 2 shows plots of concentration levels of PM₁₀ for 51 countries over a period of 17 years from 1990 to 2006.

Figure 2: Time plot of concentration levels of PM₁₀ for African countries.

Looking at Figure 2, though the levels of concentration increase at one time and decrease at another, they do not display a cyclic pattern. Some of the TS are almost linear (mostly countries with low levels of concentration). The data are irregular; hence the smoothing will be done using b-splines. There are 17 points, and 19 basis functions will be used (thus fitting saturated b-splines). Then the total curvature is penalised, with the smoothing parameter λ=10^-1. 10^-1 is the value of the smoothing parameter that minimizes the GCV as depicted in Figure 3a. The equivalent number of degrees of freedom used is approximately 10.81, as shown in Figure 3b. (Since the total curvature is being penalised, it is required that the degree of basis functions should be atleast 4, and in this case 5 is used as the degree.) Figure 4 gives the plot of the smoothed functions/curves of the PM₁₀ data.

Figure 3: Plots of GCV and degrees of freedom for different values of log (λ). 3a) Plot of values of GCV. 3b) Plot of values of degrees of freedom.

Figure 4: Smoothed curves of concentration levels of PM₁₀ for Africa.

There seems to be some resemblances and dissimilarities among the curves. Complete-linkage hierarchical algorithm is then applied on the vectors of the coefficients of the smoothed curves, and by doing so the original TS are clustered. The dendrogram represented in Figure 5 provides the visualization of the data and the possible clusters available. Large gaps (dissimilarities) are noticed to appear starting at a height of around 600 (then 600 is considered to be the cut-off). The cut-off chosen provides two clusters.

Figure 5: Dendrogram showing the merging of clusters of PM₁₀ concentration levels. The ISO ALPHA-3 CODE of countries have been used to identify the countries.

Figure 6 gives the smoothed curves of the concentration levels of PM₁₀ after clustering. The thick lines are means for the clusters while the thick dashed lines are the ±2 standard errors. Figure 7 depicts the clusters to which countries belong. The Silhouette given in Figure 8 shows how well countries are matched to their clusters.

Figure 6: Clustered curves of PM₁₀ for Africa.

Figure 7: Map of Africa showing the clusters of concentration levels of PM₁₀.

Figure 8: Graph of Silhouette for clustering of PM₁₀ data.

Applying complete-linkage hierarchical algorithm on concentration levels of PM_2.5 (2014 cross-sectional data provided by World Health Organisation [12]) results in the merging of clusters (the structure of data) depicted in Figure 9. The gaps appear to be large after a height of 60. 60 is used the cut-off. The procedure suggests that the number of optimal clusters is three. Figure 10 depicts the clusters to which countries belong [27]. Figure 11 shows how well the countries are matched to their clusters. The ARI computed for clusters resulting from the two data sets is 0.588.

Figure 9: Dendrogram showing the merging of clusters of PM_2.5 concentration levels. The ISO ALPHA-3 CODE of countries have been used to identify the countries.

Figure 10: Map of Africa showing the clusters of concentration levels of PM_2.5.

Figure 11: Graph of Silhouette for clustering of PM_2.5 data.

Looking at Figures 2 and 4, it is observed that some of the TS are not very different, especially those of countries with low concentration levels of PM₁₀. Two clusters have been extracted. One of the clusters contains 5 countries, which are Chad, Egypt, Mali, Nigeria and Sudan. The other cluster contains 46 countries namely Algeria, Angola, Benin, Botswana, Burkina Faso, Burundi, Cameroon, Central African Republic, Comoros, Congo, C^ote d’Voire, Democratic Republic of Congo, Djibouti, Equatorial Guinea, Eritrea, Ethiopia, Gabon, Gambia, Ghana, Guinea, Guinea-Bissau, Kenya, Lesotho, Liberia, Libya, Madagascar, Malawi, Mauritania, Mauritius, Morocco, Mozambique, Namibia, Nigeria, Rwanda, Sao Tome and Principe, Senegal, Sierra Leone, Somalia, South Africa, Swaziland, Togo, Tunisia, Uganda, United Republic of Tanzania, Zambia and Zimbabwe. The Silhouette provided in Figure 8 indicates that most of the countries are well matched with their clusters (in terms of PM₁₀). The average Silhouette width is given as 6.8. 6.8 is the largest average Silhouette width obtained after checking the average Silhouette widths of clusterings that have different number of clusters. Thus 2 clusters are well separated. Figures 2 and 4 show that levels of concentration of PM₁₀ had been decreasing. The decrease can easily be noticed in countries with high levels of concentration. Thus the TS had been coming together in years towards 2006, hence many TS belonging to the same cluster. This may be one of the reasons leading to only two clusters being extracted.

The second data set considered in this paper is of PM_2.5. Three clusters have been extracted from the data. One of the clusters has 3 countries, namely Egypt, Mauritania and Uganda. Another cluster has 34 countries which are Algeria, Benin, Botswana, Burkina Faso, Comoros, C^ote d’Voire, Equatorial Guinea, Eritrea, Ethiopia, Gabon, Ghana, Guinea, Guinea-Bissau, Kenya, Lesotho, Liberia, Madagascar, Malawi, Mali, Mauritius, Morocco, Mozambique, Namibia, Nigeria, Sierra Leone, Somalia, South Africa, South Sudan, Swaziland, Togo, Tunisia, United Republic of Tanzania, Zambia and Zimbabwe. The third cluster contains 14 countries and these are Angola, Burundi, Cameroon, Central African Republic, Chad, Congo, Democratic Republic of the Congo, Djibouti, Gambia, Libya, Niger, Rwanda, Senegal and Sudan. Silhouette provided in Figure 11 indicates that many countries are well matched to their clusters. The average Silhouette width obtained is 6.1. 6.1 is the maximum average Silhouette width obtained after checking the average Silhouette widths of clusterings that have different number of clusters. Thus 3 clusters are well separated.

As observed in Section 4, levels of concentration of both PM₁₀ and PM_2.5 for some African countries are similar (2 clusters have been extracted from the PM₁₀ data and 3 from PM_2.5 data). The similarities can be as a result of a variety of factors (it can be a mixture of factors). Geographical locations of countries may be considered as one of the factors affecting concentration levels of PM. In deserts, dust can be blown into the atmosphere over long distances [28]. Countries such as Chad, Egypt, Mali and Sudan which belong to the same cluster, with regard to PM₁₀ data, are located in the Sahara desert. For PM_2.5 data we have Egypt and Mauritania belonging to the same cluster and they are both in the Sahara desert. Geographical location can be considered to be contributing to similarities in levels of PM air pollution in countries.

Considering the work of Aghedo [20] in which the influence of biomass burning, biogenic, lighting and anthropogenic emissions on the troposphere ozone over Africa and globally is investigated using a coupled global chemistry climate model (ECHAM5-MOZ), it is observed that there are similarities in the sources of PM air pollution in a number of regions. Figures 12-14 show the influence of African biomass burning, biogenic and anthropogenic emissions, respectively, on the troposphere ozone. There are likely to be many factors that influence levels of PM air pollution.

Figure 12: The influence of African biomass burning on 5-year DJF (December-February) and JJA (June-August) average of the surface ozone concentrations. The figures show the difference between the reference experiment and the experiment where biomass burning emissions are excluded: Adapted from [20].

Figure 13: The influence of African biogenic emissions on 5-year DJF (December-February) and JJA (June-August) average of the surface ozone concentrations. The figures show the difference between the reference experiment and the experiment where biogenic emissions are excluded: Adapted from [20].

Figure 14: The influence of African anthropogenic emissions on 5-year DJF (December-February) and JJA (June-August) average of surface ozone concentrations. The figures show the difference between the reference experiment and the experiment where anthropogenic emissions are excluded: Adapted from [20].

Just like similarities have factors effecting, dissimilarities too have factors influencing them. The differences in clusters to which countries belong in terms of PM air pollution may be due to differences in the influence of factors ranging from geographical location to population density. Countries with much industrial activities are likely to have such activities having a bigger influence on concentration levels of PM than in countries with less of such activities.

The ARI computed for clusters resulting from the two data sets is 0.588. Thus there are some similarities in terms of members (countries) in the clusters obtained from the two data sets. The similarities in results of clusterings could be as a result of proportions of PM₁₀ concentration levels for some countries being similar to the proportions of PM_2.5 concentration levels (for the same countries).

2 and 3 clusters have been extracted from PM₁₀ data and PM_2.5 data respectively. The ARI computed for clusters resulting from the two data sets indicates that there are some similarities between the results of the two clusterings.

With limited resources, clustering of PM-related aspects may be advantageous. It plays a role in saving resources when representative sites (samples) are selected from clusters for a study, instead of carrying out the study in all sites. The results can be applied on similar sites which were not included in the study. In monitoring, only a small number of areas representing other areas belonging to the same clusters (sample) can be monitored. Countries can learn from other countries.

There are a number of factors that may affect clusters (number of clusters and the elements in the clusters). One of them is the smoothing approach. Using different values of parameters (such as using a different value for the number of basis functions and/or a different value for the smoothing parameter) or a different smoothing approach to smooth the data may result into results that are different from the ones obtained in this paper. The length of the TS is also another factor to be considered. As the length increases, there is a probability that two countries (curves) that in this paper are in the same cluster may not be in the same cluster due to differences introduced by extended length. Different clustering algorithms are also sometimes likely to lead to different results.

This is an era that requires effective and efficient use of resources. Clustering of environment-and climate-related aspects may ensure effective and efficient use of the scarce resources that Africa has.

The Commonwealth Scholarship Commission (CSC), the University of Glasgow, African Institute for Mathematical Sciences (AIMS), and Symon Sikwese.