Due to a large number of genes measured in a microarray experiment, it is essential to choose a small informative set of genes for distinguishing various classes of pathology [1-7]. An efficient gene selection algorithm can yield a compact gene set without loss of classification accuracy, and drastically ease computational burden of a classification task [8-13]. Furthermore, gene selection also can identify biomarker genes for diagnostic purposes in clinical settings [14]. A widely used selection strategy referred to as “univariate gene selection”, employs a selection criterion to evaluate the statistical separability of each gene individually [8,15-19]. Though univariate algorithms are simple to implement, they ignore separation information among gene combinations. It has been recognized that genes that best discriminate the different disease classes individually are not necessarily the ones that work best together [13]. In contrast to univariate algorithms, multivariate selection algorithms can incorporate the informativeness of possible gene combinations and search for an optimal gene subset [20-23].

It is noteworthy that there have been growing interests in gene interaction analysis for gene expression data in recent years [24-27], as strong gene interactions are usually observed [28,29] in genetic analyses of complex diseases. Statistically, it is feasible to use gene interactions for improving disease classification accuracy. Especially when gene expression differences across classes are not great enough, it will be important to use gene interactions to improve the classification accuracy. To our best knowledge, very few studies have examined the possibility of using the discrimination information from gene interactions for disease classification.

For gene expression data, two-gene statistical interactions partly represent covariance differences of gene expressions across different classes [30,31]. Thus, there are at least two types of discriminatory information for disease classification: gene expression differences and gene covariance differences across classes [31]. For classification analysis, most algorithms merely focused on gene expression differences among classes, and none of them took advantage of discriminatory information present in the difference of the gene covariance matrices.

In this paper, we propose a two-stage algorithm, Bayes error-based (BEB) gene selection method. One major advantage of our method is that it provides a feasible way to simultaneously take advantage of discriminatory information from gene interactions and that from gene expression differences for classification analysis. It is well known that Bayes error can provide the lowest achievable error rate for a given classification problem [32], and depends only on the gene space, not classifiers [33]. From this point of view, it is optimal to use Bayes error as a selection criterion [34,35] for searching an optimal or nearoptimal gene set in classification analyses. In this study, results based on simulation and real data analysis showed that discrimination information from gene interactions, which is ignored by other gene selection methods in classification analysis, can significantly improve the accuracy of disease classification.

For convenience, we focus on a two-class microarray experiment, e.g. presence and absence of a disease, or two subtypes of a disease. Suppose that a set G of n genes (G={g₁, g₂,…, g_n}) are measured. The gene expression data can be represented by a n×m matrix X= (x_iq) (i=1,…, n; q=1,…, m), where xiq is the gene expression level for the i-th gene of the q-th sample. Let Y (y_q = 0 or 1 denoting the biological condition, q=1,…,m) be a vector of the phenotypes for m samples. We assume that the expression data matrix X is preprocessed and normalized.

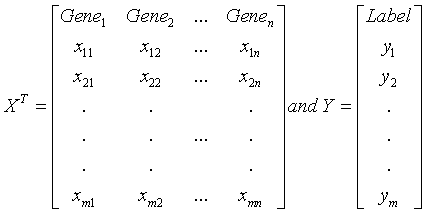
Since Bayes error for a gene set cannot be easily expressed in an analytical form, we use an upper bound of Bayes error as a selection criterion based on the Bhattacharyya distance. In addition, in expression data, an exhaustive search for an optimal gene combination is computationally intensive. Thus, our algorithm is divided into two steps: 1) Building a candidate gene pool: select genes which show differences presenting in gene covariance matrices as well as gene expression levels; 2) Search for an optimal or near-optimal gene combination from the candidate gene pool. Details of the proposed algorithm are outlined as following:

Building a candidate gene pool

This step aims to reduce the dimensionality of data by identifying a pool of candidate genes. Let 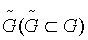denote as a candidate gene pool. Staring from an empty set 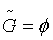, candidate genes are separately chosen and input to the set 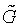based on their strengths for the phenotype discrimination, which are evaluated by two statistics. The two statistics are defined as following:

(1) One is a two sample t-test which evaluates the discriminative power for each gene. The most informative genes are those with the smallest p-values.

(2) Another one is to identify gene pairs with covariance differences between classes. Since the correlation coefficient difference of one gene pair between two classes reflects the covariance difference, we adopt a metric developed by Fisher [36]:

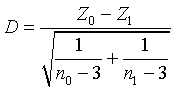                   (1)

In which z_k (k=0 or 1) is

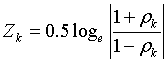                      (2)

In Equation (1) n_k is the number of samples in class k. In Equation (2) ρ_k is a correlation coefficient of a given gene pair in class k; z_k is a z-transformed correlation coefficient in class k [36]. In Equation (1) the D-value represents the correlation coefficient difference of one gene pair between two classes, and can be examined using a critical value of the standard normal distribution [37].

Search for the optimal gene set

We search for the gene set which has the minimum Bayes error upper bound based on the Bhattacharyya distance. For a given gene set, the Bhattacharyya distance is defined as:

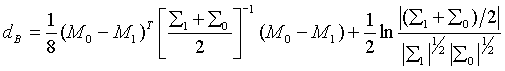           (3)

M_k and Σ_k are the gene mean vector and covariance matrix of class k respectively. As shown, the Bhattacharyya distance consists of two components: the first term gives the class separability due to the gene expression differences, and the second term gives the class separability due to the gene covariance differences. The corresponding Bayes error εB between the two classes is bounded by an upper bound ε_B*:

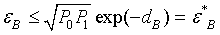        (4)

Where P_k is prior probability of class k. Due to matrix singularity of Σ, it might be difficult to directly calculate the Bhattacharyya distance. In this case, we use the principle component analysis to get Σ= Pdiag{λ₁,…, λ_r}P^T , where λ₁≥λ₂≥……≥λ_r are eigenvalues of Σ and P is an orthogonal matrix. We select S principle components which can account for a cumulative percentage of total variation of Σ, e.g. 90 percent. We use the following matrix

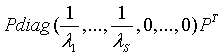
As the approximate estimate of Σ^-1, and the product of these S Eigen values are approximate estimate of .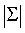

In this algorithm, a sequential backward search is applied to find the optimal (or near optimal) gene set [10,38-41]. The search process starts from a full set of candidate genes yielded from step1, and then removes sequentially the most irrelevant ones according to ε_B*. To find the most irrelevant gene of the current gene subset, one of the genes (e.g. the i-th gene) is removed, then the corresponding ε_B* for remaining genes is calculated (this is denoted as ε_B* (i)). After that, the i-th gene is returned to the subset and the (i+1)^th gene is removed. This procedure works until the genes are over. Finally, the most irrelevant gene, whose removal produces the lowest ε_B* value, can be found. The procedure is repeated until all of the genes are removed.

Simulation study

We conduct simulations in two different scenarios to evaluate the effect of gene covariance differences on classification accuracy. For conciseness, only two classes are considered in simulations. Suppose that each class includes 30 samples, and in each class, genes are separated into L non-overlapping blocks containing 2 genes each. To simulate these genes in each class, a multivariate normal distribution is applied to generate the expression profiles for the two classes. The genes are generated from a multivariate normal distribution with mean 0 and standard deviation 1. The following is the covariance matrix for class 1:

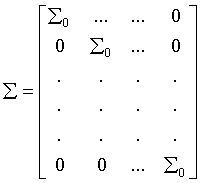
Where Σ₀ is a 2×2 symmetric matrix with “1” on the diagonal and “ρ” off-diagonal (ρ is the correlation coefficient between two genes since the variance of each gene is set as 1). In simulation settings, the gene correlation coefficients of each block appear difference across the two classes. For example, in class 1, the correlation coefficients of two genes of block L are set to ρ, while in class 2 the corresponding ones are equal to -ρ.

In scenario 1, let L=1 and vary ρ as five levels (ρ {0.90, 0.80, 0.70, 0.60, 0.50}); in the scenario 2, we set ρ=0.70 and vary the number of block L as five levels ( L {1, 2, 3, 4, 5}). In each simulation, 50 testing samples are generated for estimating classification error rates, and 1,000 replications are carried out. In our simulations, adopt two classifiers, K Nearest Neighbor (KNN) and linear Support vector machine (SVM) for the classification analyses.

The results for two scenarios are depicted in Figure 1. As shown in Figure 1A, the classification error rate decreases as ρ increases. The greater the correlation coefficient difference of gene pairs between two classes is, the lower the classification error rate is. For example, when ρ is 0.90, for KNN method one gene pair can achieve a classification error rate as low as 17.17%. It indicates that gene covariance differences between two classes can be used to improve the classification accuracy, even though there is no difference of gene expression across classes. It is noted that KNN method can more effectively take advantage of information from covariance difference of gene pairs than SVM method, and gain higher classification accuracy.

Figure 1: Classification error rates for two simulation scenarios.

In Figure 1B, it shows that when more gene pairs with covariance differences are involved in classification analyses, KNN method can achieve great improvement of classification accuracy. For KNN method, the classification error rate decreases from 29.93% to 17.66%, when the number of gene pairs varies from 1 to 5. For SVM method, when the number of gene pairs increases, SVM leads to poor performance of classification. The results of SVM method suggest that more gene pairs with covariance difference cannot effectively improve classification accuracy for SVM method.

Real microarray data

In this section we demonstrate our algorithm on two publicly available gene expression microarray datasets: DLBCL (Distinct types of diffuse large B-cell lymphoma) dataset and Leukemia dataset. We compare our method with other two gene selection strategies: The first is based on a univariate method, t-test (TTB), which evaluates the statistical separability of each gene individually; the second is based on a multivariate method, Mahalanobis distance (MDB), which utilizes expression differences from multiple genes between classes. In our study KNN and SVM are used to demonstrate the performance of the three methods. We assess these methods on the basis of classification error rate from “Leave-One-Out Cross Validation” (LOOCV) [42]. The LOOCV method proceeds as follows: hold out one sample for testing while the remaining samples are used to make the gene selection and train the classifier. Note that to avoid selection bias; gene selection is performed using the training set. The genes are selected by three methods using the training samples and then are used to classify the testing sample. The overall test error rate is calculated based on the incorrectness of the classification of each testing sample.

DLBCL dataset

DLBCL dataset was taken from the study of Alizadeh et al. [43]. DLBCL is the most common subtype of non-Hodgkin’s lymphoma. The DLBCL dataset involves 47 samples, among which 24 samples are from “germinal centre B-like” group and 23 samples are from “activated B-like” group. After the expression intensity quality filter as in the original publication, each sample contains 4,026 genes [43]. The complete microarray dataset is available at http://llmpp.nih.gov/ lymphoma/data.shtml.

In LOOCV procedure, for TTB method, 50 top ranked genes are selected for classification; for MDB method, gene selection is carried out based on those 50 genes selected from t-test; for our method, the gene selection is based on a candidate gene pool, which consists of 50 genes selected from t-test and a number of gene pairs with FDR<0.04 [44] selected by Fisher’s test. The classification results by three methods respectively are summed up in plots shown in Figure 2, with the number of genes along the x-axis and the classification error rate along the y-axis. Among three methods, BEB method generally achieves the lowest classification error, 0.00% with fewer genes over the KNN and SVM methods as shown in Figure 2A and 2B respectively. When using the KNN classifier, BEB method yields classification error rate as low as 0.00% with 30 genes, while the lowest classification error rate is 2.13% for MDB and TTB methods. Compared with MDB method, the only difference is that BEB method take advantage of the covariance differences among genes between two classes. It indicates that the usage of the covariance difference among genes can improve the classification accuracy for KNN classifier. Compared with TTB method, BEB method not only involves the information from gene covariance differences, but also removes those redundant genes due to high correlations among genes. For the SVM classifier, BEB method is slightly superior to the MDB method. According to our simulation results above, although the covariance differences among genes can aid to decrease classification error rate for SVM classifier, the effect of gene covariance differences is so limited, as shown in the Figure 2B.

Figure 2: Performance comparison of three methods on DLBCL dataset. A: is for KNN method; B: is for SVM method.

Leukemia dataset

Leukemia dataset was provided by Golub et al. [16], with the expression levels of 7,129 genes for 27 patients of acute lymphoblastic leukemia (ALL) and 11 patients of acute myeloid leukemia (AML). After data preprocessing, 3,051 genes remain. The Leukemia dataset is downloaded from: http://ligarto.org/rdiaz/Papers/rfVS/

In LOOCV procedure, three methods are carried out just like the DLBCL dataset, except that for BEB method a number of gene pairs with FDR<0.01 are selected by Fisher’s test. The classification results by three methods respectively are summed up in plots shown in Figure 3. Among the three methods, BEB method generally achieves the lowest classification error, 0.00% with fewer genes, over the KNN and SVM methods as shown in Figure 3A and 3B respectively. For the KNN classifier, BEB method achieves classification error rate as low as 0.00% with 5 genes and the lowest classification error rates is 0.00% and 2.63% for MDB and TTB methods respectively. Though MDB method also can achieve the classification error rate 0.00%, it is obvious that BEB method has better classification stability than the MAD method. As shown in the Figure 3A, the classification error rates of BEB method are 0.00% from 5 genes to 34 genes. This indicates that the involvement of genes with covariance differences can not only decrease the classification error rate, but also make the classification results more stable. For the SVM classifier as shown in Figure 3B, the classification results of MDB and BEB methods are obviously superior to the TTB method, and BEB performs similarly with MDB method.

Figure 3: Performance comparison of three methods on Leukemia dataset. A: is for KNN method; B: is for SVM method.

In this study, we present the ability of gene interactions to improve disease classification accuracy, and propose a novel gene selection algorithm which can utilize the discriminatory information of gene interactions, as well as gene expression differences across different classes. The idea behind our method is to absorb the maximum amount of informative genes which include not only the genes which are individually associated with the given phenotypes, but also the genes that in pairs discriminate given phenotypes.

In classification analyses, the aim of gene selection is to find out an optimal or near-optimal subset of genes, leading to a low classification error rate. However, it is always hard to find out an optimal gene set based on two facts: 1) A gene selection method should exhaustively traverse all candidate subsets of genes to identify an optimal one. The number of gene combinations increases exponentially as the number of genes increases, and as a result, the selection of an optimal subset of genes by exhaustive search is impractical and computationally intensive. 2) According to the Bayesian decision theory, Bayes error can provide the lowest achievable classification error rate for a given classification problem (see details in [34,45]). The problem of gene selection is equivalent to determining an informative subset of genes which can minimize the Bayes error. However, although Bayes error is the best criterion to evaluate a gene set and identify an optimal gene set, the Bayes error for a gene set cannot be easily expressed in an analytical form for estimation.

To find an optimal gene subset, our algorithm is designed to address the two abovementioned problems from three aspects. First, the step of candidate gene selection is proposed to select the informative candidate genes. Conventional gene selection methods ignore the effects of gene interactions for classification analyses. Our method incorporates the discriminatory information from gene interactions as well as gene expression differences, and thus avoids the loss of information for classification. Second, an alternative way of directly using the Bayes error as gene selection criterion is applied by minimizing an upper bound of Bayes error based on the Bhattacharyya distance [32]. This makes it feasible to take the Bayes error as a gene selection criterion. Third, a sequential backward search is employed to avoid intensive computations and derive an optimal or near optimal gene set.

In summary, the novelty of our method is that we provide an efficient way to take use of more information hidden in the dataset, especially information contained in the gene interactions that is usually ignored by most gene selection methods. According to our results, information contained in the gene interactions can play an important role in improving classification accuracy in high dimensional data. The proposed method can effectively perform gene selection with reasonably low classification error rates and a small number of selected genes.

We thank Dr. Lei Zhang for discussion of some technical issues in this study. The investigators of this work were partially supported by grants from National Institutes of Health (R01 AR050496, R21 AG027110, R01 AG026564, R21 AA015973, and P50 AR055081), and Shanghai Leading Academic Discipline Project (Project Number: S30501).