Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
+44-77-2385-9429
ISSN: 2168-9792
+44-77-2385-9429
Research Article - (2016) Volume 5, Issue 1
With a help of a local airline, the aim of this paper is to construct a cost efficiency charts, for three given aircraft to operate in three independent sectors. These chart are generated by an Excel code, the efficiency charts would be useful for airlines and fleet planners in their decision making process
<Keywords: Cost efficiency charts; Fleet planning; Direct operation cost
The intent of this paper is to calculate the cost efficiency for three aircraft namely B737-500, A319, and A320 for prescribed sectors. The cost efficiency is to be calculated using the flight data provided by an airline and the output was assessed for two possible flight scenarios. The cost efficiency charts would be useful for airlines and fleet planners in the discussion making, and in-depth rout analysis. The two routs considered here are Jeddah to Medina (JED to MED) and Jeddah to Riyadh (JED to RUH). All trips would be assumed as round trip flights. Table 1 shows the selected engine type for the study
| Aircraft Type | Engine Type |
|---|---|
| B737-500 | CFM56-3B1R |
| A 319 | CFM56-5A4 |
| A320 | CFM56-5B4/P |
Table 1: Aircrafts specification.
The first step in all scenarios was to determine the flight utilization. This was done by stating values for the time to climb and descend, and the associated climb and descent speed, along with various associated distances.
The take-off weight of each of the aircraft is calculated by the weight fraction method as identified in Figure 1, [1]. Since the empty weight was known for each aircraft, the total weight and fuel weight is easily determined.
Figure 1: Calculating the fuel and takeoff weight through the weight fraction method Ref [1].
The first step would be to calculate the payload weight Wpl from equation 1
Wpl = number of passengers ×(174 + 40) (1)
The second step would be to calculate the fuel weight Wf from equation 2
Wfl = (1−Mff )Wto ×Wfuel res (2)
Where Mff if the fuel fraction calculated, the fuel fraction ware calculated in each phase of flight, startup, taxi, take off, climb, decent and landing
The Wto is the assumed takeoff weight for the aircraft at this flight, while the fuel fraction in cruise is calculated from equation 3
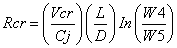 (3)
(3)
Where
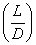 Lift to drag ratio
Lift to drag ratio
Cj specific fuel concumtion in lb/lb/hr
Vcr aircraft crusing speed in kts
Rcr cruise range in n.m
The thread step would be to calculate the operating weight empty Woe equation 4
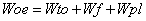 (4)
(4)
The forth step would be to calculated the empty weight from equation 5
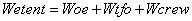 (5)
(5)
Where
Wcrew from mission specification
Wtfo trapped fuel and oil
Wtfo=5% Wto
The empty weight then is compared from the empty weight allowable from Ref1 equation 6
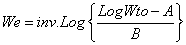 (6)
(6)
Where A, and B are constant from page 47, [1], [Table 2]
| Parameter | value |
|---|---|
| Annual salary paid for one pilot [$/year] | 100000 |
| Annual salary paid for for one co-pilot [$/year] | 80000 |
| Cost of maintenance materials for airplane [$/n.m] | 404 |
| Cost of maintenance materials for engine [$/n.m] | 217 |
| Annual hull insurance rate [$/$/year] | 0.015 |
| Maintenance manhours per flight hours [hrs/hr] | 5.86 |
| Number of flight hours / year | 750 |
| Fuel density FD [lbs/gallon] | 8 |
| Fuel price FP [$/gallon] | 1.4 |
| L / D | 15 |
| engine maintenace labor rate [$/hr] | 12 |
Table 2: Some data given Ref [3].
If the error between Wetent calculated and We is less than 5% then the Wetent is acceptable and Wf, and Wto, are acceptable if not change the Wto
Note: all dimensions are in Ib
Figure 1 summarize the process in which all weights are calculated.
Next the actual Direct Operating Cost DOC, components is calculated. The DOC is calculated by using the method used in [2], starting with the DOC of flight. Within the DOC of flight the cost of the crew, fuel and oil, and insurance all can be directly determined. All values for the crew cost were assumed based on the values from the local airline and [3]. As were the input values for the fuel and oil cost and insurance. [Table 2].
DOC=DOCfly+DOCmaint+DOCdepr+DOClnr+DOCfin (7)
Where:
DOCfly is the direct operating cost of flying in $/n.m.
DOCmaint is the direct operating cost of maintenance in $/n.m.
DOCdepr is the dirct operating cost of depreciation in $/n.m.
DOClnr is the direct operating cost of landing fees, navigation fees, and taxes in $/n.m.
DOCfin is the direct operating cost of finance in $/n.m.
n.m. nautical miles
The DOCfly is given by
DOCfly=Ccrew+Cpol+Cins (8)
Where
Ccrew is crew cost given by
Ccrew=SUM [(ncj) {(1+ Kj)/Vbl} (SALj/AHj)+(TEFj/Vbl)] (9)
ncj is the number of crew member of each type (i.e. captain, and co-pilot)
Vbl is the airplane block speed in n.m/hr.
SALj is the annual salary paid to crew members of each type
AHj is the number of flight hours per year of each type
TEFj is the travel expense factor
Kj factor which accounts for items such as vacation pay, cost of training
Cpol is the fuel and oil cost per nautical mile given by
Cpol=1.05 (Wf/R) (FP/FD) (10)
Wf is the fuel weight in lb
R range in n.m
FP is the price of fuel in $/gallon
FD is the fuel density in lbs/gallon
Cins is the airframe insurance cost in $/n.m given by
Cins=(fins) (AMP)/{(Uann) (Vbl)} (11)
fins is the annual hull insurance rate in $/$/year
AMP is the airplane market price
Uann is the annual hour utilization
The DOCmaint is given by
DOCmaint=Clab/ap+Clap/eng+Cmat/ap+Cmat/eng+Camb (12)
Where
Clab/ap is the labour cost of airframe and systems in $/n.m
Clab/ap=1.03 (MHRa) (R/Vbl) (13)
MHRa is number of airframe and systems maintenance
hours needed per block hours
Clap/eng is the labour cost of engines in $/n.m
Clap/eng=1.03 (1.3) Ne (MHRe) (R/Vbl) (14)
Ne number of engines
MHRe is the number of engines maintenance hours needed per block hours
Cmat/ap is the cost of maintenance materials for the airframe and systems $/n.m
Cmat/eng is the cost of maintenance materials for the engines $/n.m
Camb is the applied maintenance burden in $/n.m.
The DOCdepr is given by
DOCdepr=Cdap +Cdeng +Cdav +Cdapsp +Cdengsp (15)
Where
Cdap is the cost of airplane depreciation without engines in $/n.m
Cdeng is the cost of engine depreciation in $/n.m
Cdav is the cost of depreciation of avionics systems in $/n.m
Cdapsp is the cost of the depreciation of airplane spare part in $/n.m
Cdengsp is the cost of the depreciation of engine spare part in $/n.m
The DOClnr is given by
DOClnr=Clf +C nf+Crf (16)
Where
Clf the direct operating cost due to landing fees in ($/n.m) are calculated by
Clf=(Caplf)/{(Vbl) (t)} (17)
Where
Caplf is the landing fees per landing given by
Caplf=0.002Wto $/lbs (18)
Wto is the airplane takeoff weight in lbs
Cnf the navigation fees in $/n.m
Cnf=(Capnf)/{(Vbl) (t)} (19)
Where
Capnf is the navigation fees charged per airplane per flight
Crt is the direct cost of registry taxies in ($/n.m) are calculated by
Crt=(frt) DOC (20)
Where frt is a factor suggested from [3]
Frt=0.00 +(10-8) Wto (21)
Where
Wto takeoff weight in lbs
The DOCfin is given by
DOCfin=0.07 DOC (22)
In order to calculate the cost per aircraft per trip and the cost per seat mile, it is calculated as follows
Cost per aircraft per trip=DOC [$/n.m] × Distance [n.m] (23)
Cost per seat mile=DOC [$/n.m] ÷ Number of seats (24)
More details are available in [2].
The the DOC of maintenance was calculated, mostly based on the values from a local airline and values founded in [2]. This was also true for the DOC of the depreciation, as well as the DOC of the landing and navigation fees. Once all of these components were calculated, the total direct operation cost could be calculated by just adding these values together, for each of the flight scenarios. The unite of DOC is dollars per nautical miles
After calculating DOC, and with the known distance and the seats for each aircraft at each sector, the cost efficiency chart could be generated and determined (Table 3).
| DOC in $/n.m | ||
|---|---|---|
| Aircraft Type | JED - MED | JED - RUH |
| B 737-500 | 15.3 | 15.0 |
| A 319 | 16.6 | 16.3 |
| A 321 | 21.0 | 20.5 |
Table 3: Direct operating cost in $ per n.m.
Figures 2 and 3 shows the efficiency of each aircraft at a given sector. Different aircraft types are not only compared with their trip cost but also with their seat mile cost, the lower the two parameters for the given aircraft the better, the aircraft is said to be more efficient if both parameters are low.
Figure 2, shows the cost efficiency chart results for the sector Jeddah to Riyadh, Figure 3 shows the cost efficiency chart results for the sector Jeddah to Medina.
• In the cost efficiency chart the best-performed aircraft in this sector would be the lowest seat mile cost and the lowest aircraft trip cost.
• B737-500 has the highest seat mile cost but the lowest trip cost for each sector.
• A321 has the lowest seat mile cost but has the highest trip cost.
• Since it is preferential to have the lowest seat mile cost and the lowest trip cost the A319 performed better than the B737-500 and A321.