Advances in dairy Research
Open Access
ISSN: 2329-888X
ISSN: 2329-888X
Research Article - (2015) Volume 3, Issue 4
Keywords: Mozzarella cheese production, Italian buffalo, Milk yield
Adjusting the estimated mozzarella cheese production for the ratio between the individual yield and the average yield of the lactation year, will impact Italian buffalo selection in the near future. In fact, this procedure might increase the number of high-yielding buffalo with positive genetic values for mozzarella cheese production and for Fat and Protein percentages. It will mean increasing the profit for farmers that transform the whole milk in mozzarella cheese.
As compared to cow milk, buffalo milk is richer in fat, crude protein, total solids, vitamins and minerals [1-3], but fat is lower in cholesterol content [2]. Due to its high dry matter content, buffalo milk is very suitable for processing, with a cheese yielding higher than that of cow’s milk [2]. In fact, to produce 1 kg of mozzarella cheese is required 8 kg of cow's milk, but only 4 kg of buffalo milk. Although those excellent proprieties, buffalo milk price is not always influenced by its chemical and physical characteristics (eg: protein and fat percentage), but primarily by its volume. In Italy, buffalo milk is almost entirely processed into a high quality and much appreciated cheese named PDO Mozzarella di Bufala Campana.
Since the establishment of the Herd book (1977), there have been an increase of milk, fat and protein yields in the Mediterranean Italian buffalo population. This increase is primarily due to a change in feeding techniques [2,4]. From 1995 to 2013, the number of registered buffalo in Italy is increased by 47% (from 22,374 to 56,812, [5]). The economic relevance of the Italian buffalo breed is due to the high market demand for the buffalo mozzarella cheese, resulting in a price for buffalo milk almost three times the price for milk of cow. The Italian Buffalo Breeders’ Association maintains a selection scheme to improve milk and mozzarella cheese yield. The production of mozzarella cheese for 270-d of lactation (PKM, kg) is estimated from the observation of milk, fat and protein, by the formula of Altiero et al. [6]. This formula takes into account the amount of milk yield (MY), the percentage of protein (PP) and fat (FP), by using the formula of Altiero et al. [6]:
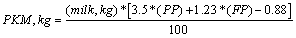
The formula shows that increased production of mozzarella cheese can be obtained mainly by increasing MY and PP. FP has less influence on mozzarella cheese production than PP. However, in the literature studies that show a positive correlation between milk yield and mozzarella cheese production were not found. Although in the buffalo species the genetic variance of the k-caseins have not been fully explained [7], there might be animals in the population with different variance of the k-casein related to a higher and lower cheese yielding attitude. And, for these animals, the estimation of cheese yield of milk, proteins, and fats would not explain their real mozzarella cheese yielding potential. Therefore, if selection is aimed to improve mozzarella cheese production in the Italian buffalo population, this fact must be taken into account. Otherwise, animals whose real cheese yield is underestimated, would not be selected from the population. Therefore, a correction to the actual PKM trait that takes into account the individual estimated cheese yield as a trait for selection of the high-yielding females in the population, it is necessary.
The objectives of this study were to investigate the effect of correcting individual estimated PKM [6] by its estimated yield on the average yield of the lactation year on genetic parameters and sire ranking in Italian Mediterranean Buffalo.
Data for 337,158 lactation records of 136,525 buffalo were analyzed. All records were extended to 270 days for lactations less than 270 days. The complete dataset included records from first to fifth lactations of all buffalo born after 1987. Editing consisted of accepting only lactation records of buffalo having more than 150 or less than 570 days of lactation and having, in the current lactation, calving to conception intervals (days open) between 20 and 730 days. Parities were grouped into three different classes: parities 1, 2 and ≥ 3. Days open (DO) in the current lactation were approximated by taking the difference between two consecutive calving intervals and subtracting the length of the average buffalo gestation period (310 days). For first lactations, an average DO of 170 days was assigned. Lactation records were grouped into seven DO classes: DO were rounded to the nearest month to form classes corresponding to months 1 to 6. Month’s ≥ 7 constituted the last class. Contemporary groups were formed by grouping records of buffalo calving in the same herd in the same year and a season of calving within the year. Three seasons of calving were defined: January to April; May to August; and September to December. This dataset was reduced by removing records in contemporary groups in herds with number of observations less than five for the variance components estimation and less than two for the genetic evaluation. Individual corrected PKM (APKM) was obtained by multiplying the PKM by the ratio of its estimated yield (EY) and the mean estimated yield (MEY) of the year that the lactation refers to as follows:
APKM=PKM*c;
where:
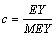
EY=[3.5*(PP)+1.23*(FP)-0.88]
To evaluate the effect of correcting the individual PKM for the ratio EY/MEY on genetic parameters and sire ranking in Italian Mediterranean Buffalo, estimates of variance components and sire EBVs were obtained for APKM and PKM and the results were compared.
Estimates of variance components for APKM and PKM and sire EBVs were obtained with the following mixed model:
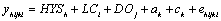
where yijhkl is APKM or PKM in kg of milk with twice daily milking and lactation length adjusted to 270 d, HYS is the effect of herd-year-season class h; LCi is the effect of age at calving-parity class i; DOj is the effect of calving to conception class j; ak is the additive genetic effect of animal k; ck is the permanent environmental effect associated with buffalo k; and eijhkl is the random residual effect associated with the record. Additive genetic, permanent environmental, and residual effects were assumed to be mutually uncorrelated. Variance components and fractions of phenotypic variance were estimated from single-trait analyses using a derivative-free algorithm [8] to obtain estimates that maximize the residual likelihood (REML). Two-trait analyses were performed to obtain estimates of genetic and environmental correlations between APKM and MY and PKM and MY. The stopping criteria was set at 1 × 10-6 for the variance of–2(log likelihood) in the simplex. The number of rounds allowed was up to 250 before restarting. Local convergence was declared when the variance of the simplex was less than 10-6 after which restarts were made until convergence at global maximum was declared when-2(log likelihood) did not change to the second decimal. Simple correlations between APKM and MY and PKM and MY were also calculated with SAS [9]. Sire ranking for APKM and PKM were compared looking at their differences.
Number of lactation records, phenotypic means and standard deviations for unadjusted (PKM) and adjusted (APKM) mozzarella cheese production, are shown in Table 1.
| Trait | N | Mean | SD |
|---|---|---|---|
| PKM | 337,158 | 599.5 | 132.1 |
| APKM | 337,158 | 598.3 | 141.2 |
Table 1: Number of lactation records, phenotypic means and standard deviations (SD) for 270-day unadjusted (PKM) and adjusted (APKM) mozzarella cheese production (kg).
Unadjusted means of mozzarella cheese yield were very similar between APKM and PKM. Estimates of variance components and genetic parameters for the PKM and APKM are shown in
| Trait | σa2 | σt2 | σe2 | h2 | C2 | e2 | r |
|---|---|---|---|---|---|---|---|
| PKM | 42,244 | 22,854 | 70,155 | 0.31 ((0.028) | 0.17 ((0.025) | 0.52((0.010) | 0.48 |
| APKM | 34,470 | 28,913 | 87,159 | 0.23((0.029) | 0.19 ((0.028) | 0.58 ((0.015) | 0.43 |
Table 2: Estimates of variance components1, heritability (h2) and repeatability (r) (standard errors in parentheses) for 270-day unadjusted (PKM) and adjusted (APKM) yield of mozzarella cheese (kg).
The heritability estimates for APKM and PKM were 0.23 and 0.31, respectively. The heritability of APKM is lower than that of PKM. The relative portion of permanent environmental variance to total variance was estimated at 0.43 and 0.48, respectively, for APKM and PKM. Phenotypic and genetic correlations of PKM and APKM with MY are shown in
| Trait | N | Phenotypic | Genetic |
|---|---|---|---|
| PKM | 337,158 | 0.98 | 0.25 (0.07) |
| APKM | 337,158 | 0.86 | 0.09 (0.06) |
Table 3: Phenotypic and genetic correlation of MY with APKM and PKM.
Phenotypic correlation between MY and APKM was smaller (0.86) compared to that of MY and PKM (0.98). Genetic correlation between MY and APKM was also smaller (0.09) compared to that of MY and PKM (0.25). Since MY is the multiplier in the formula for estimating PKM, it was expected to find a larger phenotypic and genetic correlation between MY and PKM, compared to that of MY and APKM. Therefore, APKM is less influenced by MY. To show the changes in the top lists of sires ranked by their APKM EBVs and their PKM EBVs, shifts in rank for top lists was determined. The results are presented in Table 4.
| SIRE RANKING | SIRE EBVS | |||||||
|---|---|---|---|---|---|---|---|---|
| From Ranking PKM | To Ranking APKM | Differences | PKM kg | APKM kg | (APKM-PKM) kg | Protein% | Fat% | Milk kg |
| 1 | 1 | 0 | 221.3 | 188.0 | -33.3 | -0.10 | -0.46 | 969.9 |
| 4 | 2 | 2 | 140.1 | 155.7 | 15.6 | 0.15 | 0.13 | 471.9 |
| 2 | 3 | -1 | 196.3 | 151.1 | -45.2 | -0.21 | -0.52 | 955.5 |
| 3 | 4 | 1 | 177.3 | 150.1 | -27.2 | -0.15 | -0.35 | 803.1 |
| 7 | 5 | 2 | 100.6 | 124.7 | 24.1 | 0.09 | 0.46 | 295.0 |
| 6 | 6 | 0 | 120.0 | 108.5 | -11.5 | -0.10 | 0.07 | 499.3 |
| 5 | 7 | -2 | 121.3 | 94.0 | -27.3 | -0.12 | -0.61 | 584.4 |
| 14 | 8 | 6 | 62.5 | 82.6 | 20.1 | 0.11 | 0.32 | 163.1 |
| 9 | 9 | 0 | 84.5 | 81.9 | -2.6 | 0.11 | 0.03 | 287.8 |
| 12 | 10 | 2 | 66.6 | 80.6 | 14.0 | 0.12 | 0.30 | 180.4 |
| 8 | 11 | -3 | 92.6 | 76.9 | -15.7 | -0.07 | -0.18 | 411.9 |
| 16 | 12 | 4 | 52.0 | 73.0 | 21.0 | 0.22 | 0.24 | 121.3 |
| 11 | 13 | -2 | 70.8 | 64.1 | -6.7 | -0.01 | -0.12 | 296.5 |
Table 4: Shifts in rank of sires PKM EBVs compared with ranking by APKM EBVs.
In the same table are also presented the EBVs for MY, FP and PP for each sire. In general, the ranking of sires for APKM tended to increase for sires that showed positive EBVs for FP and PP, whereas the ranking of sires for PKM tended to penalize sires with negative breeding values. This trend is very clear if sires are listed from the bottom to the top of their EBVs for PP (Table 5). There is a decreasing in list for sires with negative EBVs for PP from PKM and APKM (4 sires vs 7 sires), whereas sires with positive EBVs for PP increased in list from PKM to APKM (6 sires vs 6 sires).
| SIRE RANKING | SIRE EBVS | |||||||
|---|---|---|---|---|---|---|---|---|
| From Ranking PKM | To Ranking APKM | Ranking differences | PKM kg | APKM kg | (APKM-PKM) kg | PP | FP | MY kg |
| 2 | 3 | -1 | 196.3 | 151.1 | -45.2 | -0.21 | -0.52 | 955.5 |
| 3 | 4 | 1 | 177.3 | 150.1 | -27.2 | -0.15 | -0.35 | 803.1 |
| 5 | 7 | -2 | 121.3 | 94.0 | -27.3 | -0.12 | -0.61 | 584.4 |
| 1 | 1 | 0 | 221.3 | 188.0 | -33.3 | -0.10 | -0.46 | 969.9 |
| 8 | 11 | -3 | 92.6 | 76.9 | -15.7 | -0.07 | -0.18 | 411.9 |
| 6 | 6 | 0 | 120.0 | 108.5 | -11.5 | -0.10 | 0.07 | 499.3 |
| 11 | 13 | -2 | 70.8 | 64.1 | -6.7 | -0.01 | -0.12 | 296.5 |
| 7 | 5 | 2 | 100.6 | 124.7 | 24.1 | 0.09 | 0.46 | 295.0 |
| 14 | 8 | 6 | 62.5 | 82.6 | 20.1 | 0.11 | 0.32 | 163.1 |
| 9 | 9 | 0 | 84.5 | 81.9 | -2.6 | 0.11 | 0.03 | 287.8 |
| 12 | 10 | 2 | 66.6 | 80.6 | 14.0 | 0.12 | 0.30 | 180.4 |
| 4 | 2 | 2 | 140.1 | 155.7 | 15.6 | 0.15 | 0.13 | 471.9 |
| 16 | 12 | 4 | 52.0 | 73.0 | 21.0 | 0.22 | 0.24 | 121.3 |
Table 5: Shifts in rank of sires PKM EBVs compared with ranking by APKM EBVs.
The decrease in heritability from PKM to APKM, might be due to the lower genetic correlation between APKM and MY compared to that of PKM with MY. Moreover, APKM tended to positively change sire ranking. In fact, sire ranking tended to increase for sires with positive EBVs of PP and FP. Whereas, sire ranking tended to decrease for sires with negative EBVs of PP and FP. Due to the high correlation of PKM and MY, by selecting through the PKM, one risk is to increasing the number of buffalo within the buffalo population that will produce more milk, which is not always optimal for making mozzarella cheese. In fact, their cheese yielding will depend not only on milk production but also on the type and amount of proteins in milk that are more optimal for making mozzarella cheese.
The study showed that the equation used to predict the mozzarella cheese yield is not suitable to estimate the individual milk yield. In fact, due to its large correlation with milk yield, the equation tends to under predicts the high-yield animals. Therefore, by selecting through the actual PKM, one risk is to increasing the number of animals within the buffalo population that will produce more milk, which is not always optimal for making mozzarella cheese. A A good alternative to this prediction is the use of APKM as trait for genetic selection. In fact, the APKM has a lower genetic correlation with milk yield than the actual PKM and tend to increase the ranking of sire with positive EBVs for Protein and Fat percentage. In this way, it will be possible to identify more accurately the potential bull mothers, which are genetically superior females for the cheese yielding in the population. Bulls to be evaluated by progeny testing would be chosen from their offspring.