Journal of Molecular Imaging & Dynamics
Open Access
ISSN: 2155-9937
ISSN: 2155-9937
Research Article - (2011) Volume 1, Issue 1
Vibrational spectra of lactose molecule in the solid-state have been reproduced in the 4000- 50 cm-1. The modified Urey Bradley Shimanouchi force field (mUBSFF) has been employed combined with an intermolecular potential energy function that includes Van der Waals interactions, electrostatic terms and an explicit hydrogen bond function.
The force constants established previously for α-D-glucopyranose and β-D-galactopyranose as well as the crystallographic data of α-D-lactose monohydrate were the starting parameters for the present work. Satisfying calculated frequencies with suitable assignments have been obtained. Good agreements have been found between our results and those of vibration spectra of other disaccharides and monosaccharides.
Keywords: Disaccharides, Lactose, Normal coordinate analyses, IR and Raman spectra, Solid state.
In recent years, certain advances have been made in developing software for modeling IR spectra of compounds with the use of the structure-property database. In this work, the object under study is lactose; this latter occupies a position in sugar metabolic bioprocessus. To study the chemical structures and physical properties of this kind of carbohydrates, various methods including vibrational spectroscopy have been used [1-3] for which a full and reliable interpretation of the observed spectra requires a theoretical analysis.
In this field, a number of theoretical works [4-22] have been devoted to the calculation of normal modes of vibrations of monosacharides like fucose [23], fructose [24] or methyl-galactopyranoside[25] and disaccharides like turanose and melibiose [26]. To complete the series of papers dealing with normal mode analyses of disaccharides in their crystalline environment, we have chosen to study a lactose molecule, the last is constituted by aα-(D)glucopyranose linked to β-(D) galactopyranose units.
Besides vibrational data reproduction, theoretical calculations also provide an approach to the bands assignments. Thus, because infrared and Raman techniques remain the most important and common tools for identification available in research and industrial laboratories, the goal of this paper is also to achieve a precise interpretation of spectra of this disaccharide once their corresponding force fields established. This will progressively allow, in making further assignments of some significant bands observed on vibrational spectra of bio-polymers constituted by mono- or di-saccharide sequences. An accurate spectral interpretation of saccharide molecules still remains the major difficulty, especially in the region below 1500 cm-1 [27,28], because the normal modes of vibration in this range are often the result of coupling involving different group motions [29].
The used software program involves basically the GF Wilson [30] methods in which the geometry matrix G derived from X-ray data and the initial force constants matrix F comes from previous works on similar molecules. The set of parameters constituting this latter matrix are then fitted by comparison between observed and calculated frequencies in a way to keep the difference as weak as possible.
Samples
The samples of lactose were purchased from the Sigma-Aldrich Chemical Company in powder form and used without any further purification.
Spectra
To record infrared spectra in the 4000-50 cm-1 range, a IFS88 BRÜKER FTIR spectrometer has been used, the samples have been prepared as pellets by mixing 2% w/w of sugar in KBr powder. The Raman spectra has been obtained from 4000 to 50 cm-1on the same spectrometer equipped with a FT Raman module using a laser beam having a 1046 nm wavelength. The resolution has been fixed at 2 cm-1 and 100 scans have been accumulated to realize each spectrum.
Calculation method
To calculate the normal modes of the disaccharides, the GF method of Wilson [30] was adapted, using coordinates of local symmetry developed by Shimanouchi [32]. This calculation is based on the intramolecular Urey Bradley Shimanouchi force field combined with intermolecular field [33] involving non-bonded atom pair wise interactions described by a buckingham function, electrostatic interactions and a hydrogen bonds potential. These functions have been extensively described in this work.
c-1 Intramolecular potential function: The analytic expression of this intermolecular potential energy function is :
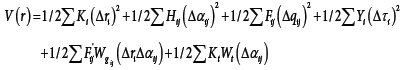
Δri : variation of the bond length.
Δαij : variation of the bond angle.
Δτi : variation of the bond torsion.
W : redundancy term.
Ki : elongation force constant.
Hij : force constant of angle deformation.
Fij : force constant of repulsion (1-3) type.
Yi : torsion constant.
F'ij : force constant due to the linear repulsion terms.
Kt : internal constant characteristic of tetrahedral groups.
Δqij : variation of the distance between atom non-bonded i and j (1-3) type.
c-2. Intermolecular potential function: The intermolecular potential energy function is the sum of three terms:
Vinter = V1 + V2 + V3
where V1 is the interaction potential between non-bonded pair of atoms and is of Buckingham type. This potential is composed of a repulsion potential energy (short distance) and of an energy of van der Waals type (long distance).
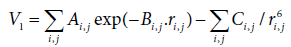
Ai,j, Bi,j and Ci,j are specific parameters to each pair of atoms Where the values of the A, B and C parameters [34,35] are given in Table 3.
V2 is the electrostatic interaction term of Colombian type.
V2 = qi . qj / ε ri,j
rij : distance separating two atoms i and j.
qi, qj : résidual charges of atoms i and j.
ε : dielectric constant. With ε=3. 0 (which gives the best results in low frequencies range) [25].
V3 is the potential of hydrogen bonds of the Urey-Bradley- Shimanouchi type.
2VH = ΣKO.H (rO.H)2 + ΣrO-H rH.O HO-H.O (ΔαO-H.O)2
+ Σ rH.O rO.C HH.O-C (ΔαH.O-C)2 + ΣrO-H rH.O HH-O.H (ΔαH-O.H)2
+ ΣYH.O (ΔτH.O)2 + ΣYO-H (ΔτO-H)2
where KO. . . H is the force constant of the bond length; HO-H.O, HH.O- C and HH-O.H are the force constants of the bond angles; YH.O and YO.H are the force constants of the torsion; Δri, Δαi,j,k, Δτi are, respectively the variations of the bond length, of bond angle and torsion.
The geometry of this molecule derives from previous crystallographic works summarized in Table 1. These molecules as well as their atom numbering are presented in Figure 1.
| N number of atoms | 48 |
| 3N-6 | 138 |
| space group | P21 |
| molecules per cells | 2 |
| number of cells | 125 |
| Number of hydrogen bond | 10 |
| a ( Å) | 7.982 |
| b (Å) | 21.562 |
| c (Å) | 4.824 |
Table 1: Crystallographical data used in e normal mode analyse.
The method of Miyazawa [36] is then used to reduce the number of internal coordinates introducing the local symmetry coordinates which must be in agreement with some conditions stated by Shimanouchi [37].
As the force constants related to the CH2OH group are weakly affected by neighboring atoms, we have treated this group in its own symmetry as isolated group as described previously by Huvenne et al. [38]. The initial force fields are those established previously for α-Dglucopyranose [12] and β-D-galactopyranose [13].
The calculations have been carried out by using C. V. O. A program; this last has been written by Takeuchi [39].
For this molecule, the calculations have been performed in two steps; at first the lower frequencies below 200 cm-1 have been calculated in the solid state (rigid body approximation), because the force constants related to hydrogen bonds in the cell system operate independently. After that, the calculations have been completed for the higher frequencies. The most important part of the presented work consists then in the refinement of the force constants in order to reach a reasonable fit between the observed and calculated frequencies.
The method of fitting the force field consists in making the differences between the calculated and the observed frequencies Δυ as small as possible, by the use of the relationship between Δυ and Δf (Δf = Δυ/J) , J being the element of the Jacobian matrix [40].
Residual charges
The residual charges are calculated using the DFT method B3LYP/6-31G (d,p), the results are presented in Table 2
| Atom | Charge | Atom | charge |
| C1 | 0.040032 | C24 | 0.372100 |
| C2 | 0.117265 | C25 | 0.169464 |
| C3 | 0.074099 | C26 | 0.175918 |
| C4 | 0.107158 | C27 | 0.121911 |
| C5 | 0.116087 | C28 | 0.152242 |
| C6 | 0.579548 | C29 | 0.013621 |
| O7 | -0.619901 | O30 | -0.65365 |
| O8 | -0.589752 | O31 | -0.64293 |
| O9 | -0.639415 | O32 | -0.82428 |
| O10 | -0.654986 | O33 | -0.70843 |
| O11 | -0.743424 | O34 | -0.70600 |
| O12 | -0.747802 | H35 | 0.214947 |
| H13 | 0.153068 | H36 | 0.209357 |
| H14 | 0.206428 | H37 | 0.179882 |
| H15 | 0.190109 | H38 | 0.175420 |
| H16 | 0.173616 | H39 | 0.177809 |
| H17 | 0.181574 | H40 | 0.194126 |
| H18 | 0.233265 | H41 | 0.175609 |
| H19 | 0.144036 | H42 | 0.351447 |
| H20 | 0.316061 | H43 | 0.348976 |
| H21 | 0.316606 | H44 | 0.502003 |
| H22 | 0.316061 | H45 | 0.360128 |
| H23 | 0.347266 | O46 | -0.66925 |
| H47 | 0.271201 | ||
| H48 | 0.397053 |
Table 2: Residuals charges calculated with B3LYP/ 6-31G(d,p) method.
| Type | A (Kcal.mol-1) | B (Å-1) | C (Kcal.mol-1) |
| C…C | 83 630 | 3.600 | 568.0 |
| C…O | 63 700 | 3.881 | 441.0 |
| C…H | 8766 | 3.670 | 125.0 |
| O…O | 96 500 | 4.333 | 346.0 |
| O…H | 57 500 | 4.727 | 122.0 |
| H…H | 2654 | 3.740 | 27.3 |
Table 3: Van der Waals Specific parameters of pair atoms.
Hydrogen bonds
Lactose molecule involves two intramolecular bonds and eight intermolecular bonds. 125 unit cells surrounding the primary one are taken into account to define all the existing hydrogen bonds. In (Table 4) are represented the experimental and calculated hydrogen bonds networks for this molecule in the crystalline state.
| Hydrogen bonds | O..H(Å) | Coordinates |
| H42(1-1)..O9(1-1) | 2,27 | (x,y,z) |
| H48(1-1)..O8(1-1) | 2,00 | (x,y,z) |
| H20(1-1)..O31(4-10) | 2,83 | (-x,y+1/2,-z+3/2) |
| H21(1-1)..Ow(3-92) | 1,91 | (x-1/2,-y+1/2,-z+2) |
| H22(1-1)..O8(4-10) | 2,05 | (-x,y+1/2,-z+3/2) |
| H43(1-1)..O7(2-19) | 2,01 | (-x+1/2,-y,z-1/2) |
| H44(1-1)..O30(4-13) | 2,29 | (-x+1,y+1/2,-z+3/2) |
| H45(1-1)..O32(3-72) | 1,93 | (x+1/2,-y-1/2,-z+2) |
| H47(1-1)..O34(3-72) | 2,72 | (x-1/2,-y+1/2,-z+2) |
| H21(1-1)..O33(2-1) | 2,07 | (-x+1/2,-y,z+1/2) |
Table 4: Hydrogen bonds of α-D-lactose.
Force constants
To carry out the initial calculations, a set of force constants coming from previous works [41,42] have been used, they consist, as cited above, in the force constants of α-D-glucopyranose, those of β-Dgalactopyranose molecules. For the calculation of intramolecular vibrations, 3N-6 degrees of freedom have been considered for the isolated molecules including three sorts of vibrations; the bond stretching modes, the bending modes and the torsional modes. The basis of the internal coordinate has been reduced by eliminating redundancies, those due to the rings and those called threeredundancies due to tetrahedral carbon groups [5].
Since some groups in the studied disaccharide differ from those present in the quoted monosaccharides, especially the linked groups, the hydroxyl and oxymethylen groups, the set of force constants had to be fitted in order to make the differences between observed and calculated as weak as possible [36,43]. Moreover, because of very complex couplings between different groups in the modes rising below 1500 cm-1, the refinement of these force constants had to be very judicious so as to not reverse the assignment of some bands. The final force constants are given in (Tables 5a-5e).
| α-D-glucopyranose (mdyne/Å) | β-D-galactopyranose (mdyne/Å) | |
| KCCY-Ccy | 2.87 | 3.13 |
| KCCY-CEXO | 2.97 | 3.60 |
| KCCY-Ocy | 3.20 | 3.20 |
| KCCY-OEXO | 3.36 | 4.32 |
| KCexo-O | 3.60 | 4.30 |
| KCCYC-H | 3.98 | 4.24 |
| KCEXO-H | 4.10 | 4.10 |
| KO-H | 5.86 | 5.61 |
| KO-H(CH2OH) | 5.77 | 5.13 |
| KOw-H | 5.39 | |
Table 5a: Force constants of stretching modes expressed in ( mdyne/Å).
| α-D-glucopyranose (mdyne/Å) | β-D-galactopyranose (mdyne/Å) | |||
| H | F | H | F | |
| Ccy-Ccy-Ccy | 0.35 | 0.25 | 0.35 | 0.44 |
| Ocy-Ccy-O | 0.30 | 0.74 | 0.25 | 0.45 |
| Ccy-Ccy-Ocy | 0.19 | 0.45 | 0.31 | 0.56 |
| H-Ccy-Oexo | 0.36 | 0.54 | 0.23 | 0.67 |
| H-Ccy-Ocy | 0.36 | 0.85 | 0.27 | 0.20 |
| H-Cexo-Oexo | 0.25 | 0.46 | 0.14 | 0.46 |
| H-Ccy-Oosy | 0.26 | 0.54 | 0.12 | 0.47 |
| Ccy-Ccy-H | 0.24 | 0.47 | 0.24 | 0.47 |
| Ccy-Cexo-H | 0.28 | 0.48 | 0.11 | 0.48 |
| Ccy-O-H | 0.45 | 0.62 | 0.19 | 0.50 |
| Cexo-O-H | 0.27 | 0.68 | 0.27 | 0.41 |
| C-Ocy-C | 0.40 | 0.42 | 0.60 | 0.42 |
| H-C-H | 0.45 | 0.07 | 0.12 | 0.07 |
Table 5b: Force constants of attractive and repulsive bending modes expressed in (mdyne/Å).
| (mdyne/Å) | |
| K Ocy- -H | 0.250 |
| K O- -H | 0.150 |
| K Ow- -H | 0.375 |
| Ocy- -H-O | 0.030 |
| Ow- -H-O | 0.040 |
| O- -H-O | 0.070 |
| C-O- -H | 0.022 |
| C-Ocy- -H | 0.032 |
| H-O- -H | 0.026 |
| O- -HW-O | 0.150 |
| Y O-Hhy | -0.008 |
| Y H- -O | -0.009 |
Table 5c: Force constants associated to the torsion modes expressed in (mdyne/Å).
| α-D-glucopyranose (mdyne/Å) | β-D-galactopyranose (mdyne/Å) | |
| Ccy-Ccy | 0.100 | 0.120 |
| Ccy-Cexo | 0.110 | 0.150 |
| Ccy-Ocy | 0.061 | 0.063 |
| Ccy-Oexo | 0.117 | 0.062 |
| Cexo-O | 0.070 | 0.068 |
Table 5d: Intermolecular force constants expressed in (mdyne/Å).
| (mdyne/Å) | |
| KA C1 | 0.095 |
| KA C2 | 0.040 |
| KA C6 | 0.071 |
| l C1 | 0.015 |
| l C6 | 0.015 |
| l C29 | 0.015 |
Table 5e: Tensions and kappa force constants around the tetrahedral carbons (mdyne/Å).
The comparison between the initial and final force constants (Tables 5a-5e) shows that the principle of transferability stated by T. Shimanouchi is confirmed. Indeed, when considering α-Dglucopyranose or β-D-galactopyranose units the only force constants that are modified in regards to the initial ones are those related either to CH2OH or hydroxyl groups. This is due to the fact that the first one may have a different orientation because of the presence of intra and intermolecular hydrogen bonds and the second one may be involved in a different hydrogen bond network. The remaining force constants do not vary from a disaccharide to the other.
The force constants of attractive (H) and repulsive (F) related to bending modes are shown in Table 5b, one observe differences for the vibrations involving CCO, CCH, HCO and COH groups that are mainly due to the ring configuration (alternative or normal form) [18]. Some weak changes concerning the force constants related to the cyclic C-C-C, C-C-O and O-C-O bending modes are observed for the pyranose ring (Table 5b).
Again, for the force constants related to the torsional modes of the cyclic C-C and C-O (Table 5c) one can note any significant changes. However, for the C-O ones belonging to the exocyclic CH2OH groups, some changes are observed. This fact is in agreement with our statement cited here above.
Vibrational analyses
Table 6 (included as supplementary data) summarizes the calculated frequencies, PED, and absolute IR and Raman intensities of normal vibrations of the lactose molecule and presents the assignment of the observed absorption bands in the spectrum of this compound.
The 3700 cm-1-2800 cm-1 range
This region is divided into two sub region, the first between 3700 cm-1 and 3000 cm-1 for the stretching vibrations of OH. The position and shape of these bands are used to obtain information on the hydrogen bonds can be formed with the OH [44,45]. The second of 3000 cm-1 to 2900 cm-1for the CH stretching type.
1-a) The 3700 cm-1-3000 cm-1 sub range: In the IR spectrum of lactose several bands are observed at 3528 cm-1, 3378 cm-1, 3359 cm -1, 3331 cm-1, 3294 cm-1, 3316 cm-1, 3272 cm-1 and 3209 cm-1, all of these bands are attributed to stretching vibrational modes of O-H bonds. Theoretical calculation gives almost the same result and basing on percentages distribution of potential energy, the vibrations are approximately pure (Table 6 (included as supplementary data)).
In frequency range under consideration, the OH stretching modes related to the oxymethylene group CH2OH was calculated at 3375 cm-1 for glucose unit and 3358 cm-1 for galactose unit. For following previous studies [14,15,41,46-49], the OH stretching modes was calculated in this range at 3362 cm-1.
Lactose is monohydrate sugar, a stretching vibrational modes of OH of water is calculated at 3553 cm-1 for this disaccharide. The same mode was calculated at 3569 for α-D-melibiose and 3552 for D-turanose [26].
1-b) The 3000 cm-1 -2800 cm-1 sub range: In the zone of the C-H stretching modes, the bands are more intense into Raman than IR. In this range, we were interested in C-H vibration of CH2OH groups (symmetric and anti-symmetric vibration), this mode is largely affected by the various orientations of hydroxyl group. However, the intermolecular hydrogen bonds contribute enormously to these frequencies.
For lactose, a symmetrical mode of vibration coupled with an antisymmetric mode was calculated at 2897 cm-1 and 2865 cm-1 for the unit of glucose, for galactose unit these modes are calculated at 2878 cm-1 and 2918 cm-1. These modes were calculated below 2900 cm-1 for glucose [41] and galactose [42] what confirms our results.
The 1500 cm-1-1200 cm-1 range
This zone has very many bands utilizing very coupled movements, bringing into play the different deformations of CH2OH group , but also the angular deformations of CCH, OCH, HCH and COH type [4,14,50]. The bands characteristic of scissoring modes of HCH group are observed at 1457 cm-1 and 1367 cm-1 on the Raman spectrum of lactose, on the IR spectrum they are observed at 1456 cm-1. For lactose in solution this mode is observed at 1461 cm-1 [3,25,51]. Dauchez et al. [15] have calculated the scissoring mode at 1461 cm-1 and 1456 cm-1 for maltulose monohydrate, and at 1468 cm-1 and 1459 cm-1 for cellibiose, and 1470 cm-1 and 1455 cm-1 for gentibiose. This difference in the Raman spectrum may be explained by the position and the configuration of the glycosidic linkage.
Between 1490 cm-1 and 1200 cm-1 the calculated bands are due to movements of CCH and OCH. In this range, our results are in perfect agreement with those obtained for monosaccharides [41], disaccharides [52], and polysaccharides [32]. The modes CCH and OCH is coupled between them and with other modes like the elongations of C-O and deformations of COH [54].
In the IR spectrum, two bands of a significant intensity are observed, the first is observed and calculated at 1382 cm-1, the second at 1338 cm-1. These bands are due respectively to deformations of OCH and CCH. This is confirmed by the work of Buslov et al. [53] who have calculated these modes respectively at 1381 cm-1 and 1340 cm-1 for α-D glucose.
The 1200 cm-1-900 cm-1 range
Between 1200 and 900, the adjustment of the frequencies is very difficult, because in this range the bands are very coupled between them, only the distribution of the potential energy obtained by theoretical calculation makes it possible to assignment these bands.
In the IR spectrum and according to the results of theoretical calculation, the frequencies are mainly due to the C-C and C-O stretching as well as to the deformations of atomic groups OCH, COH and CCH. The bands between 1200 cm-1 and 1000 cm-1 are assignment to the elongations of an endocyclic and exocyclic C-O bonds and C-C, the latter are coupled with angular deformations of COH, OCH, CCH and HCH [4,10,12,44,54,55].
The frequency calculated at 1091 cm-1 and observed at 1095 cm-1 for lactose is assignment to C-O endocyclic elongation for galactose unit, this band is calculated at 1032 cm-1 for the unit of glucose. In this region the exocyclic modes of C-O are observed and calculated respectively to 1084 cm-1, 1165 cm-1 and 1141 cm-1.
The elongation of the osidic bond is generally localized between 1200 cm-1 and 900 cm-1 [56]. The band corresponds to this vibration is observed at 1120 cm-1 in the Raman spectrum of lactose, it is calculated at 1121 cm-1. The presence in the experimental spectrum of a number of additional bands as compared to theoretical data can be due to the factor group splitting of fundamental modes of molecules in the crystalline cell [57].
The 900 cm-1-800 cm-1 range
This zone is named anomeric region or fingerprint, for this area, Tul'chinsky et al. [51] have called this region "region of crystallinity" and it is difficult to make exact assignments of the frequencies because it characterizes anoméres α and β. Nevertheless, this region contains several strongly coupled types of vibration of CCO and COC groups, rotations of CH2OH groups, elongations and torsions of C-C and C-O. In this range few bands are observed and calculated.
The bands observed to 877 cm-1 and 852 cm-1 on the Raman spectrum of lactose are well reproduced and which are due respectively to the rocking of CH2 group and the torsion of C-O endocyclic of galactose. Normal coordinate calculations performed by different authors [4,10,12,44,54,55] also show that the frequencies of two fundamental vibrational modes fall within the 900-800 spectral range.
The 800 cm-1-600 cm-1 range
This range is known as area of crystallinity [52]. Between 800 cm-1 and 700 cm-1 the vibrational modes are due to torsions of the endocyclic and exocyclic of C-O, coupled with other vibrations such as the deformations C-O-C, C-C-H and C-O-H.
The band observed at 759 cm-1 in the Raman spectrum of lactose and calculated at 756 cm-1 is due to endocyclic torsion C-O of the unit of glucose, while the band observed to 732 cm-1 and calculated to 731 cm-1 is due to exocyclic torsion of C-O of the same residue.
The distribution of the potential energy shows that in the interval between 700 cm-1 and 600 cm-1, the vibrational modes are very coupled, in this region the band observed at 671 cm-1 and calculated at 669 cm-1 is due mainly to the rocking (Ro) of CH2 group.
The 600 cm-1-200 cm-1 range
The range of the spectrum below 600 cm-1 is characteristic of each saccharide [53]. According to the data of theoretical calculation, in the 600-200 cm-1 range lie mainly the frequencies of complicated coupled vibrational modes involving both deformations of angles formed by CCO, CCC, OCO, COC and torsional vibrations of hydroxyl groups [12,58].
Between 600 cm-1 and 350 cm-1, the bands are very intense into Raman, in IR they are average. The band calculated at 495 cm-1 and not observed on the spectrum IR of lactose is due to the deformation of CH2 group. The band observed at 400 cm-1 and calculated to 405 cm-1 is due to torsion C-C, the band observed at 377 cm-1 and calculated at 378 cm-1 is assignment to deformation of CCO. The vibrational modes of COC (osidic bond) deformation group was calculated at 349 cm-1, this band is coupled with torsions of C-C and C-O. For lactose in solution this band is observed at 350 cm-1 [4].
The range below 200 cm-1
The bands observed and calculated between 200 cm-1 et100 cm-1 are mainly due to torsions of C-C and which are coupled with torsions of C-O. The domain below 100 cm-1 corresponds to the overall movements of the lattice due to the modes of translation (Tx, Ty, Tz) and rotation around the axes of inertias (Ra, Rb, Rc). These modes are coupled with intra and intermolecular vibrations, in particular with torsions of C-C and C-O. For example the band observed at 157 cm-1 and calculated at 156 cm-1 for lactose is assigned to the torsion of C-O, this band is also observed in the Raman spectrum of isomaltulose, it was calculated at 152 cm-1. The bands below 70 cm-1 are due mainly to a crystal vibration because it is due essentially to the translational and rotational modes.
In this work, we reproduced the vibrational spectroscopic data of lactose starting from the modified Urey Bradley Shimanouchi potential function. The comparison of the force constants obtained for this molecule shows that there is not a great difference in their numerical values. Thus the principle of transferability established by Shimanouchi has been validated. Consequently, the force field obtained for this study will be very useful for the calculation of the vibrational normal modes of other more significant molecules like the oligosaccharides and polysaccharides, who contains a similar units of our studied molecule.