Journal of Geography  & Natural Disasters
Open Access

High Obliquity, High Angular Momentum Earth as Moon’s Origin Revisited by Advanced Kinematic Model of Earth-Moon System

Bijay Kumar Sharma^{* *}Correspondence: Bijay Kumar Sharma, Department of Electronics and Communication, National Institute of Technology, Patna, Bihar, 800005, India, Tel: +919334202848, Email:

Author info »

Introduction

Keplerian era

The Kepler’s Third Law for a given Planet-Sun configuration is:

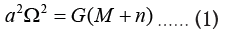
Equation (1) does not specify if the given orbital configuration is stable. Newton derived this law assuming that centripetal force

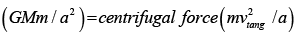
Where a=semi-major axis of Earth-Moon orbital configuration, M=Mass of the Earth and m=mass of our Moon. By implication it was assumed that all configurations predicted by (1) are stable. By the end of 19th century George Howard Darwin put a question mark on this stability by publishing two papers on E-M system [1,2]. In 18th Century, German Philosopher Kant had suggested the theory of retardation of Earth’s spin based on the ancient records of Solar Eclipses [3,4]. Similar kind of studies had been carried out by Kevin Pang at Jet propulsion Laboratory at Pasadena [5,6]. Kevin Pang happened to step upon certain ancient records regarding Solar Eclipses. A total Solar Eclipse had been observed in the town of Anyang, in Eastern China, on June 5, 1302 B.C. during the reign of Wu Ding. Had Earth maintained the present rate of spin, the Eclipse should have been observed in middle of Europe. This implies that in 1302 B.C. i.e. 3,291 years ago Earth’s spin period was shorter by 0.047 seconds. This leads to a slowdown rate of 1.428 seconds per 100,000 years. In 1879 George Howard Darwin carried out a complete theoretical analysis of Earth- Moon System and put forward a sound hypothesis for explaining the slowdown of Earth’s spin on its axis. This marked the end of Keplerian Era. Gravitationally bound bodies were necessarily tidally interacting and tidal interaction led to tidal dissipation with inherent instability and hence a post-Keplerian physics was required to deal with gravitationally bound binary pairs. Tidally dissipative system because of loss of energy cannot be stable. The system will evolve to a minimum energy state which is a stable configuration by necessity.

The beginning of evolutionist view of universe

By mid 20^th century it was increasingly felt that celestial bodies pair behave as electrons orbiting the nucleus in individual atoms. Within an atom electrons had radiation-less stable permissible orbits propounded by Niels Bohr in 1913:

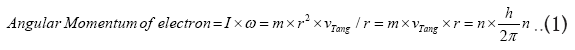
Equation (1) Simplifies to de Broglie standing wave condition:

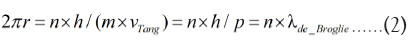
Equation (2) simply states that electrons are permitted to stay in radiation-less stable orbits where electrons behaving as matter wave forms a Standing Wave and is inhibited from making synchrotron radiation and ensured stable orbits. Any other orbit would collapse and electron would be launched on a death spiral towards its respective nucleus.

In exactly the same manner celestial body binaries are born at aG1 (inner Clarke’s Orbit) which is a Keplerian Orbit, an equilibrium orbit where centripetal force is exactly balanced by centrifugal force but it is an energy maxima (Shown in S5 of Supplementary file) hence the secondary tumbles short or tumbles long of aG1. In 2002 at World Space Congress, Houston, Author proposed Kinematic Model (KM) (As shown in S4 of Supplementary file). According to KM celestial body pairs have two triple synchrony orbits (aG1 and aG2) where they are conservative systems and no dissipation of energy is involved [7-9]. Here triple synchrony orbits implies:

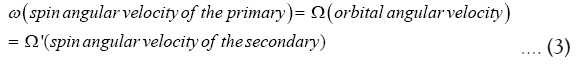
The orbits of triple synchrony are defined as geo-synchronous orbits in E-M system and Clarke’s orbits in context of planet-satellite pairs, star-planet pairs, star-star pairs, Neutron Star pairs (NS) and NS and BH (Black Hole) pairs.

• Planet-satellite pairs, star-planet pairs and star pairs are non-relativistic systems. They, within months/years, lock-in at outer Clarke’s orbit unless impacted by a third celestial body. Non-relativistic systems are stable at outer triple synchrony orbits.

• NS pairs, NS and BH pairs or BH pairs are relativistic systems. Relativistic systems are radiating gravitational waves and they are being driven towards coalescence hence they are always experiencing in-spiral collapse until the final ring-down and merger and always negatively off-setted with respect to outer Clarke’s Orbit and never locked-in at outer Clarke’s orbit. The magnitude of off-set is decided by the relativistic strength of NS pair/NS-BH pair/BH pair which in turn is decided by the rate of apsidal precession (long axis of the elliptical orbit of the planet turning in the same direction as the planet’s orbital motion).

Two competing schools of thought on tidally interacting binaries

The whole scientific community was using the elasto-viscous model for analyzing the tidally interacting binaries but this was based on the knowledge of Love number and Q factor of the celestial bodies which in turn depended on the knowledge of density, rigidity, viscosity and rate of periodic forcing. These parameters are known with large uncertainties for different Planets and their Satellites and hence their Tidal Evolutionary History will be arrived at with equal uncertainty in Seismic Model based analysis (Shown in S3 of Supplementary file). The Author developed a Kinematic Model (KM) of E-M system to study its tidal evolutionary history from its birth to the final lock-in orbit or to its final doom (As shown in S4_KM section in Supplementary file). The KM required only the globe-orbit parameters and the age of the system. Since the system parameters were known with high degree of confidence level hence the results arrived at were reliable and accurate. In spite of this improvement KM failed to resolve the conundrum in E-M puzzle. This had baffled the whole scientific community.

The conundrum of E-M puzzle

The Apollo mission had confirmed the age of E-M system with high degree of certainty as 4.467 Gy [10,11]. With this age of E-M system the present rate of recession of Moon should have been 2.4 cm/y but Lunar Laser Experiment operational since 20th July 1969 was giving a recession rate of 3.82 ± 0.07 cm/y which indicated anomalously high dissipation rate in Earth’s oceans and continents. If the present rate of recession was assumed and extrapolated into the past it led to the birth of Moon at 2.8 Gy. In addition the KM with age as 4.467 Gy was not giving a matching theoretical formalism of observed LOD curve based on Coral fossils [12] and ancient tidalites (Shown in S4.3 of Supplementary file). The reconstruction of the history of Lunar recession from existing data of tidal rhythmites [13] and that of Length Of Earth Day (LOD) record in coral fossils [12] indicate that Earth-Moon is not just a Clockwork or orbitally fixed pair of monoliths as viewed by Newton in Mathematica Principia but instead Earth-Moon system is a tidally evolving system where Moon is tidally receding from Earth since its birth. The findings of Stephenson [14] and Lambeck [15] firmly established that Earth-Moon system is a non-linearly tidally evolving system with a complex history of interrupted tidal evolution due to intermittent gravitational resonances with lunar M2 tides and solar S2 tides. Kant [16] hypothesis included the lunar tidal perturbation as well as solar tidal perturbation on tidal evolution of E-M system. Darwin [1,2] clearly established that Moon’s tidal brake and Solar tidal brake have slowed down the Earth’s spin from 5 hrs and orbital radius of 18,000 Km (just beyond Roche’s Limit) [17] to the present Earth’s spin rate of 24 h and orbital radius of 384,400 Km and in the process the Earth’s angular excess spin energy released has led to tidal heating of Earth and spin angular momentum of Earth spin has been transferred to E-M orbital angular momentum and Lunar tidal recession. The results seem to indicate a non-linear variable rate of tidal dissipation throughout E-M system’s history. Oceans may enter and exit M2 and S2 tide resonance in geologically short time intervals [18]. It was this tension between observation and theory which compelled the Author to remove the first degree approximations from E-M model and propose a more comprehensive and detailed model of E-M system which the Author is referring to as Advanced Kinematic Mode; (AKM) and as will be shown in this paper AKM has dramatically improved the model to real world correlation. (Shown in S6 of Supplementary file).

Materials and Methods

Materials

The origin of Moon from high obliquity, high Angular Momentum (AM) Earth and impact generated circum-terrestrial debris disk: Matija Cuk et al. [19] have proposed a new model for the birth and tidal evolution of our natural satellite Moon in which lunar tidal dissipation due to lunar obliquity tides during Cassini State transition plays an important role in stabilizing and allowing E-M system to arrive at climatically favorable E-M configuration with a low Earth’s obliquity (φ=23.44°). High angular momentum and high obliquity Earth provides a more robust mechanism to remove excess AM and provides Earth’s mantle like isotopic composition properties of Moon. Their proposal is as follows:

Stage 1: A high energy collision between Earth and Theia (Mars-like impactor) impact generated debris (which is iron depleted and hence Moon has unusually small metallic core <3% of total mass of Moon) forms a circum-terrestrial accretion disc coplanar with the equatorial plane of highly oblique Earth (φ >70°) [20]. The impact resulted in well mixed vaporized and equilibrated molten material from which both Earth’s crust and mantle and Moon formed. This resulted in identical isotopic signatures of Earth and Moon [21,22]. Impact had peeled off the mantle of Earth. Old canonical theory assumes the initial terrestrial day to be 5 hr but Cuk et al. [19], have done their simulation using 2 hr terrestrial day. Extraordinary impact left rapidly spinning highly oblate Earth with a tilt angle of φ >70° with respect to the ecliptic.

Stage 2: Laplace plane transition at lunar orbit at ‘a’ (semi-major axis of lunar orbit)=17 R_E [23]. This abrupt transition from geo-centric Laplace plane to heliocentric Laplace plane , due to solar secular perturbation in highly oblique Earth’s environment, excites sizeable lunar eccentricity, high lunar orbit inclination (α=30°) and draining of AM from lunar orbit to Earth’s helio-centric orbit. Simultaneously Earth’s obliquity falls from 70° to 30°. The lunar eccentricity causes large stretching and squeezing of Moon leading to internal tidal flexing within Moon. This causes strong eccentricity damping satellite tides. These eccentricity damping Moon’s tides balance the Earth’s tides and stall the tidal evolution for a prolonged period [24]. During this stalled period, Moon’s orbital plane inclination increases to α=30°. Hydrostatic equilibrium shape of Moon at ‘a’=15 to 17 R_E with Moon’s orbit eccentricity at 0.2 got frozen because of rigid lithosphere and that fossil oblateness is retained till the modern times [25].

Stage 3: Earth becomes rigid enough to maintain C (principal moment of inertia of Earth around spin axis)=8.01910^37^2Kgm×− constant from ‘a’=25 R_E to the present day at ‘a’=60.33 R_E. At ‘a’=30 R_E to 40 R_E, lunar spin axis underwent Cassini State Transition [26,27].

Moon’s obliquity increases from β=10° to 50°. This generates strong and forced lunar obliquity tides which help suppress the lunar orbital inclination from α=30° to 10°. Simulation study show that from ‘a’=29.7 to 35 RE, Moon is in non-synchronous state and beyond 35 R_E to the present 60.33 R_E, Moon is locked in a synchronous orbit with its face always showing towards Earth. Moon is tidally locked with Earth. At 33 R_E, Cassini State transition occurs while transiting from Cassini state 1 to Cassini state 2. Moon’s Obliquity (β) is as high as 70°. Once Moon settles in Cassini State 2, Moon sedately spirals out from Earth. The inclination angle is dampened from 30° to 15° due to Moon’s obliquity tides (tidal flexing within the interior of our Moon).

Stage 4: from ‘a’=30 RE to ‘a’=60.33 RE (in modern times), lunar obliquity tides bring down φ=30° to φ=23.5° and α=15° to α=5° at the same time ensuring the current value of AM [28]. Here there is a conundrum. As Moon’s orbital plane inclination drops from 15° to 5°, Earth’s obliquity must rise from 0° to 23.5°. This requires that at Cassini State Transition Earth’s obliquity φ must be 0. Rubicam [29] has discussed this problem. At present, the Earth’s mean obliquity is slowly increasing as a result of tidal interactions with the Moon. The lunar inclination is decreasing at the same time, so the angular momentum of the Earth–Moon system is conserved. The conservation of total angular momentum is given as follows [29]:

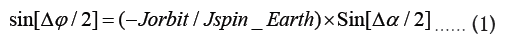
This implies that if lunar orbital plane inclination angle decreases by 5° and Jorbit/ Jspin_Earth=10 then Earth’s obliquity must increase by 60.6°. This precisely is predicted by Advanced Kinematic Model as seen by close examination of Figure 1.

Methods

The total resultant angular momentum vector of Earth-Moon system.

Calculation of total Angular Momentum (AM) of Earth-Moon system as the vector sum of constituent AMs:

J0, J1 and ecliptic normal are coplanar according to Cassini Law 3.

Presently E-M system is in Cassini State II hence J0 vector and J1 are on the two sides of Ecliptic Normal as shown in the Figure 1.

J3, J2, J4 and Ecliptic normal are coplanar.

But the plane containing J0, J1 and Ecliptic Normal and the plane containing J2, J3, J4 and Ecliptic normal are two separate planes hence J0 and J1 are shown by dotted lines.

Definitions of Earth’s Obliquity (φ), Moon’s orbital plane inclination (α) and Moon’s Obliquity (β):

Axial tilt of Earth’s spin axis with respect to write Ecliptic Normal=φ=23.44°=0.4091051767 radians; Axial tilt of Moon’s spin axis write Ecliptic Normal=β=1.54°=0.02687807 radians;

Angle between Moon’s equatorial plane and ecliptic plane=β;

Total axial tilt of Moon’s spin axis write E-M orbital AM vector=α+β=6.68°=0.11658 radians.

All these are observational Astronomy data in the current era.

The total resultant angular momentum vector of Earth-Moon system: According to Cassini Law, Moon’s spin axis Normal to the equatorial plane of Moon, Moon’s orbital plane Normal and Ecliptic plane Normal are co-planar hence these three NORMALS can be drawn on the same page but Earth’s spin axis are not co-planar hence Earth’s spin will be kept out while determining the resultant angular momentum J3=vector sum of J0 and J1 of E-M system.

Cassini’s laws, three empirical rules that accurately describe the rotation of the Moon, formulated in 1693 by Gian Domenico Cassini. They are:

• The Moon rotates uniformly about its own axis once in the same time that it takes to revolve around the Earth;

• The Moon’s equator is tilted at a constant angle (β=about 1.54° of arc) to the ecliptic, the plane of Earth’s orbit around the Sun; and

• The ascending node of the lunar orbit (i.e., the point where the lunar orbit passes from south to north on the ecliptic) always coincides with the descending node of the lunar equator (i.e., the point where the lunar equator passes from north to south on the ecliptic). As a consequence of the third law, the north pole of the Moon as projected on the sky (point z), the north pole of the ecliptic (point Z), and the north pole of the lunar orbit (point P, inclined at an angle of about=α=5.14° to the ecliptic) all lie close to one another on a great circle. Total Angular Momentum Vector of E-M system is determined in two parts. In first part: J0 the orbital angular momentum and J1 Moon’s spin angular momentum and the Ecliptic Normal are taken coplanar and co-processing and J0 and J1 are placed on the two sides of the Ecliptic Normal since for lunar semi-major axis ‘a’>33 R_E E-M system has settled down in Cassini State II. And AKM is valid within the range 45 R_E <a<60.33 R_E hence E-M system being in Cassini State II is a valid assumption. In second part: J2 the spin angular momentum of oblique Earth, the ecliptic plane normal and J3 the vector sum of J0 and J1 will be treated as co-planar and the vector sum J4=J2+J3 will be determined.

Determination of J3 vector=J0 vector+J1 vector: Here J0 (orbital angular momentum of E-M system and J1 (spin angular momentum of Moon) and Ecliptic normal are coplanar hence the vector triangle ABC can be drawn on one plane.

Sum of the interior angles=180°=π=3.14 radians Hence ∆ABC the sum of the interior angles: a+b+c=3.149 But c=π– (αβ+)=3.14-0.116588=3.025012654 radians Working out the vector sum of constituent angular momentum vectors, we arrive at the following results:

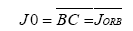(Earth-Moon system) is normal to the Moon’s orbital plane and Moon’s orbital plane is inclined to ecliptic plane by α=5.14° and sidereal orbital period=27.3217 d

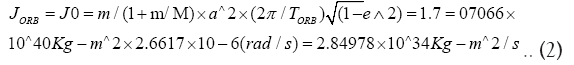
Here ‘a’ (semi-major axis of Moon’s orbit)=

3.844 × 10⁸ m; mass of Earth M=5.9723 × 10²⁴ Kg and mass of our Moon m=0.07346 × 10²⁴ Kg,

m/(1+m/M)=reduced mass of Moon=7.25674 × 10²² Kg,

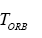Orbital period of Moon around Earth (sidereal period)=27.3217 d and e is eccentricity=0.0549.

Moon’s spin angular momentum is in the direction of Moon’s spin axis normal to Moon’s equatorial plane.

As seen in Figure 1, Moon’s spin axis is tilted write Ecliptic normal by 1.54° and tilted write orbital normal by 6.68° to the right of the orbital normal because presently we are in Cassini State II

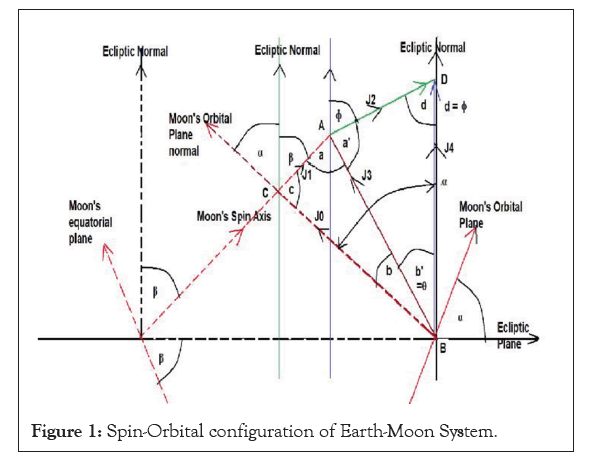
Figure 1: Spin-Orbital configuration of Earth-Moon System.

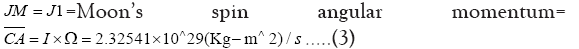
Where

R_Moon=1737.4Km

I=moment of inertia of Moon,

Ω=spin angular velocity of Moon.

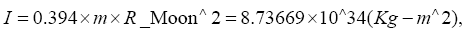
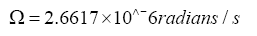
Since Moon is in synchronous orbit:

Moon’s spin period=Moon’s orbital period=27.3217 d …. (4)

As seen in Figure 1:

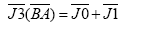
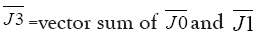
From Δ∆ABC in Figure 1 we obtain:

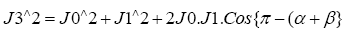
Where α=5.14°=0.08970992355250854 radians;

β=1.54°=0.02687785118484197 radians and

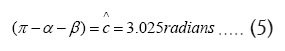
(5) can be simplified to:

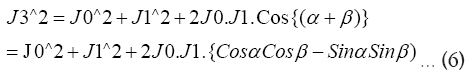
Here we define the following Trignometric Identities:

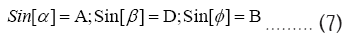
Substituting these identities in (6) we get:

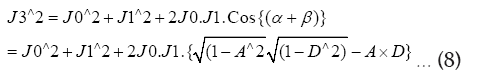
For modern times values of inclination and lunar obliquity we obtain:

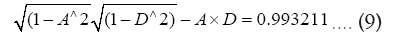
Sunstituimg (9) and the magnitudes of J0 and J1 we obtain:

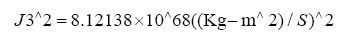
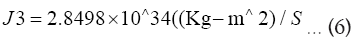
Inspecting Figure 1, we see that J3 makes an angle θ with respect to the normal of the ecliptic and J3 lies left to the normal.

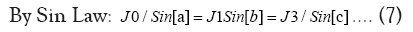
From (7) the three angles are:

angle c=(3.14 − 0.116588)=3.02501265 radians, angle b=9.49129 × 10^-7 radians and

angle a=0.116579 radians and a+b+c=π …….. (8)

The angle of inclination of J3 write ecliptic normal and left to normal=θ=α –b=0.08970905087 radians=5.13995⁰ ~ α ;

Determination of J4 vector=J2 vector+J3 vector=Total AM of E-M system: For calculating the total resultant angular momentum J4 we have to consider ∆ABD in Figure 1.

Applying Cos Law to ABD we get

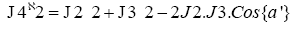where θ=0.08970905087 radians,

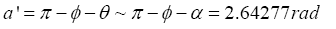
For the period from a=45 RE to a=60.336 R_E Moon’s spin AM is several order of magnitudes smaller than orbital AM hence it is valid to assume that angle )’~ (aπϕα−−hence total AM J4 is given as follows:

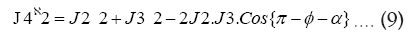
(9) simplifies to the following:

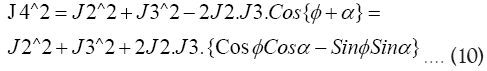
Substituting the Trignometric identities in (10) we obtain:

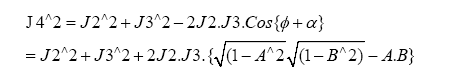
Taking the modern values of terrestrial Obliquity and lunar orbital inclination:

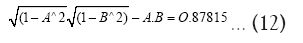
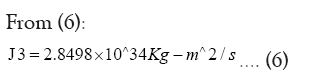
Earth’s spin axis obliquity with respect to (write) the ecliptic normal=Φ=23.44°=0.40910 radians;

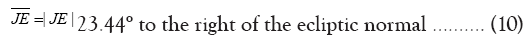
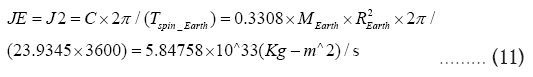
Where sidereal spin period=23.9345 h,

Volumetric mean radius of Earth=6371.008 km,

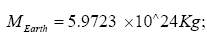
Substituting the magnitudes of the parameters we get:

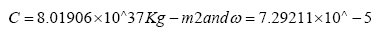
Substituting the numerical values in (9);

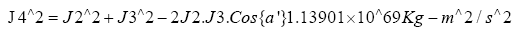
Therefore:

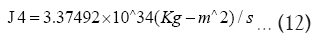
To determine the angles b’ and d the Sine Law is used namely:

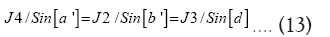
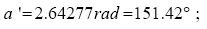
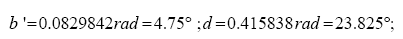
The sum of the internal angles comes to be: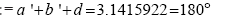

Therefore total angular momentum of E-M system is:

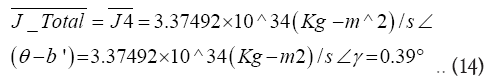
In scalar analysis,

Eccentricity was assumed to be zero.

By vector analysis of AM of E-M system very simple picture emerges.

In real world situation, vectorial total angular momentum of E-M system has been constrained to be almost but not exactly normal to ecliptic plane after Laplace Plane Transition and its magnitude has remained constant at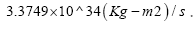

So the vector diagram of Figure 1 is valid in assuming that total AM J4 has remained invariant for last 1.5 Gy and has remained coincident with the Ecliptic Normal.

Results

Our Moon has been born at inner geo-synchronous orbit, aG1. E-M system has tidally evolved from inner geo-synchronous orbit, aG1, to the outer geo-synchronous orbit, aG2. It is midway in this evolutionary path at a=384,400Km from the center of the Earth. At both the geosynchronous orbit E-M system is in triple synchrony state when X=1.

We obtain triple synchrony time period at aG1 and aG2 as 5 hours and 44.6 solar days respectively.

The methodology for arriving at the above result is given below.

Determination of the initial and final lock-in orbits and orbital period=spin period of Moon=spin period of Earth at initial and final lock-in orbit

Rewrite (8)

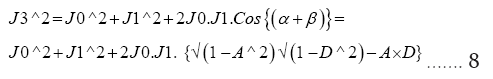
Rewrite (11) and substitute (8) in (11):.

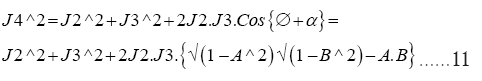
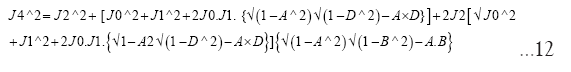
Let us redefine J0, J1, J2 J3

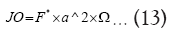
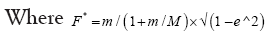
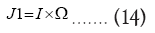
Substituting (13), (14) and (15) in (12) we obtain:

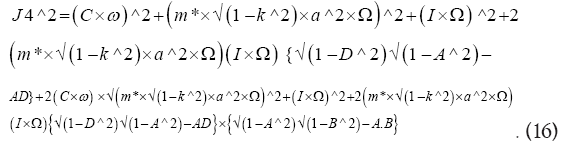
Divide (16) by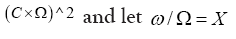

We get:

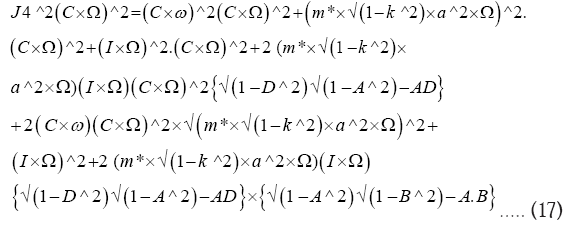
Simplifying (17)

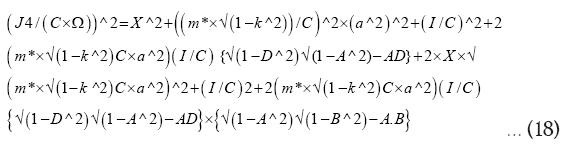
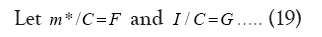
Substitute (19) in (18) we get:

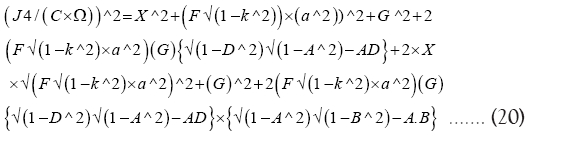
Substituting Kepler’s third law:

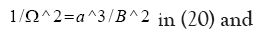
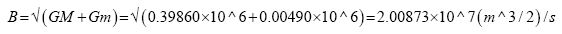
We get:

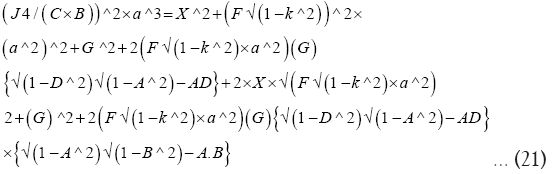
Let J4/ JCBN×=…. (22)

Substituting (22) in (21) we get:

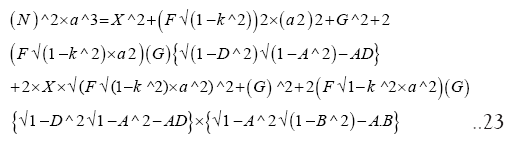
In ideal case where Lunar Orbital Inclination 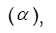Earth’s obliquity (φ) and Moon’s obliquity (β) are zero then

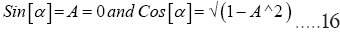
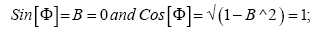
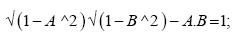
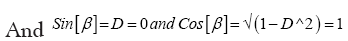
Substituting the above results in (23)

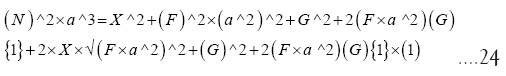
(24) simplifies to classical KM equation:

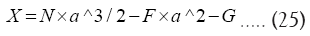
(25) Is the classical form being used by the Author for Kinematic Modelling with assumptions that Moon’s orbital plane Inclination, Earth’s Obliquity and Moon’s Obliquity are zero degree angle. F and G have been defined in (19) and N has been defined in (22).

Substituting the numerical values of the system parameters we get:

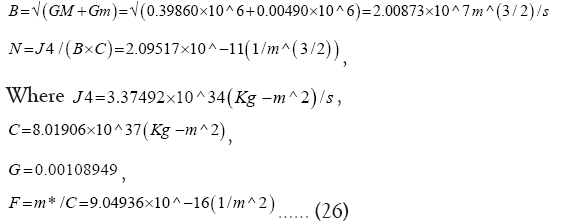
Our Moon has been born at inner geo-synchronous orbit, aG1. E-M system has tidally evolved from inner geo-synchronous orbit, aG1, to the outer geo-synchronous orbit, aG2. It is midway in this evolutionary path at a=384,400 Km from the center of the Earth. At both the geosynchronous orbit E-M system is in triple synchrony state when X=1.

(24) Simplifies to (25) because at the two end points E-M system is locked-in triple synchrony with

Equating (25) to Unity we obtain the two geo-synchronous orbits.

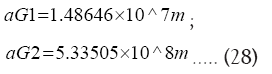
Using Kepler’s third law:

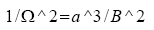
We obtain triple synchrony time period at aG1 and aG2 as 5 hours and 44.6 solar days respectively

Calculation of observed LOM/LOD= ω/Ω= 27.3217

In E-M system LOM (length of month)=sidereal lunar month and LOD (length of day)=the sidereal day.

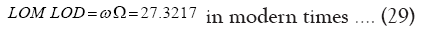
In Section 7, LOM/LOD equation has been formulated in (23) and it is being restated here:

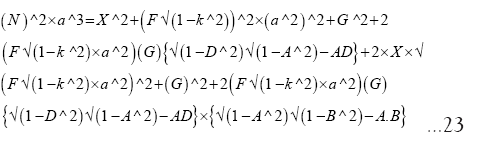
If real world is considered then:

Using current Earth’s obliquity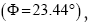 current Moon’s orbital inclination 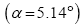and current Moon’s obliquity 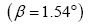and k= 0.05491 8 we obtain the following trigonometric identities:

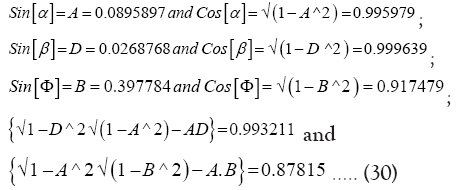
Solving (42) with numerical values of N, F and G and ‘a’ (the current semi-major axis) substituted we get the following quadratic equations:

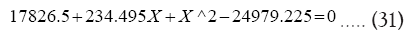
The two roots of (31) are: -261.815 and 27.3199. The negative root is rejected since both the spin of Earth and Moon and orbital motion are retrograde. Hence only 27.3199 is tenable. We are having a perfect match with observed LOM/LOD.

(23) is satisfied for the current epoch ω/Ω (LOM/lOD), α (Inclination angle) , β (lunar obliquity), φ (terrestrial obliquity) and e (eccentricity).

Evolution of inclination of Lunar orbital plane, eccentricity of Lunar orbit and obliquity of Moon’s spin axis based on the information in Cuk et al. [19]

The empirical relation describing the evolution of Moon’s orbital plane inclination with respect to the ecliptic is (Appendix A1):

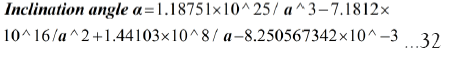
The empirical relation describing the evolution of Moon’s obliquity angle (β) is given as below (Appendix S2):

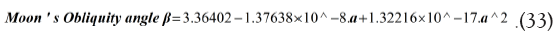
The empirical relation describing the evolution of Moon’s orbit eccentricity is (Appendix A):.

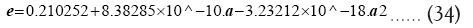
The determination of the evolutionary history of Earth’s obliquity from advanced kinematic model of tidally interacting E-M system.

From a previous personal communication arXiv: http://arXiv.org/abs/0805.0100

LOM/LOD of Earth Moon system is known over the tidal evolutionary history. It is tabulated in Table 1.

In Appendix S1, the evolutionary history expression have been derived for LOM/LOD and Earth’s obliquity φ (radians). They are as follows:

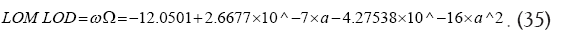
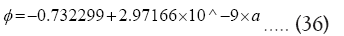
Using (23)

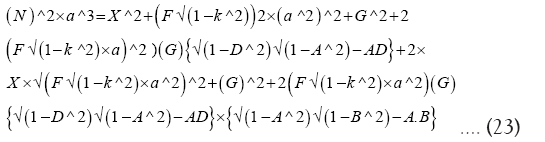
Obliquity angle is determined. In (23) all constant and all spatial functions are known except the obliquity angleφ. For a given lunar orbit, LOM/LOD is known. Using this information Sin[φ] is determined and hence φ and tabulated in Table 1. We have six set of data from a=30 R_E to the present day semi-major axis. We clearly see that at Cassini State Transition, Earth’s obliquity is indeterminate. From 40 R_E to 60.336 R_E it is well behaved and obliquity is increasing. It increases from 1.22483° to 23.44°. This means that during angular momentum conservative phase reduction in inclination is accompanied with increase in obliquity by necessity. Table 2 gives the evolutionary history of ω/Ω (LOM/lOD), α (Inclination angle), β (lunar obliquity), φ (terrestrial obliquity) and e (eccentricity)

Table 1: LOM/LOD and Earth’s Obliquity for past geological epochs

Table 2: Evolutionary history of ω/Ω(LOM/LOD), α(Inclination angle),  β(lunar obliquity),  φ (terrestrial obliquity) and e (eccentricity).

In Figure 2, the evolution of Earth’s obliquity () based on AKM data and based on Simulation data by Matija Cuk et al. [19] is given. We see the discontinuity at 45 R_E.

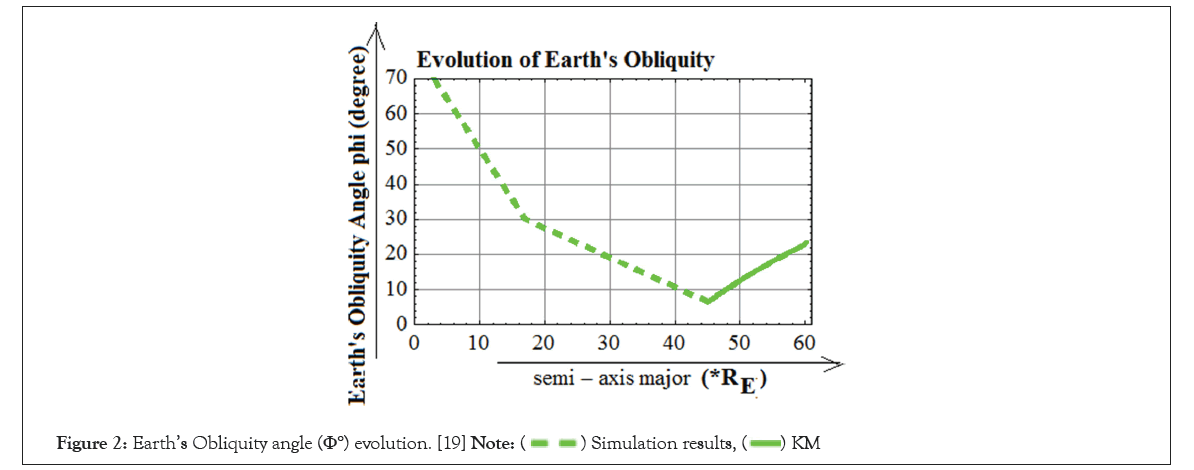
Figure 2: Earth’s Obliquity angle (Φ°) evolution. [19]

In Figure 3, the evolution of Moon’s orbital plane inclination (α) based on AKM and based on Simulation done by Matija Cuk et al. [19] is given. Here there is a continuity.

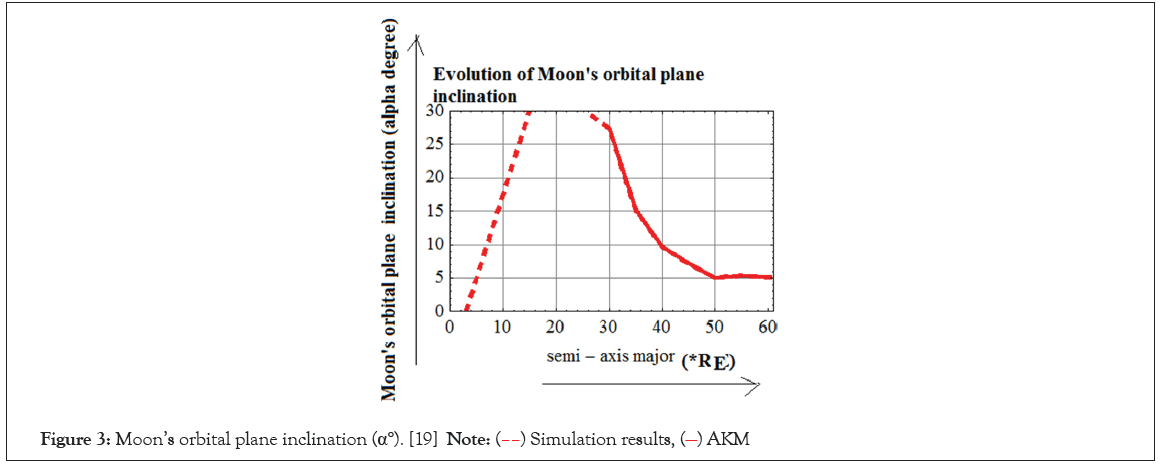
Figure 3: Moon’s orbital plane inclination (α°). [19].

In Figure 4, the evolution of Moon’s obliquity (β) based on AKM and based on Simulation done by Matija Cuk et al. [19] is given.

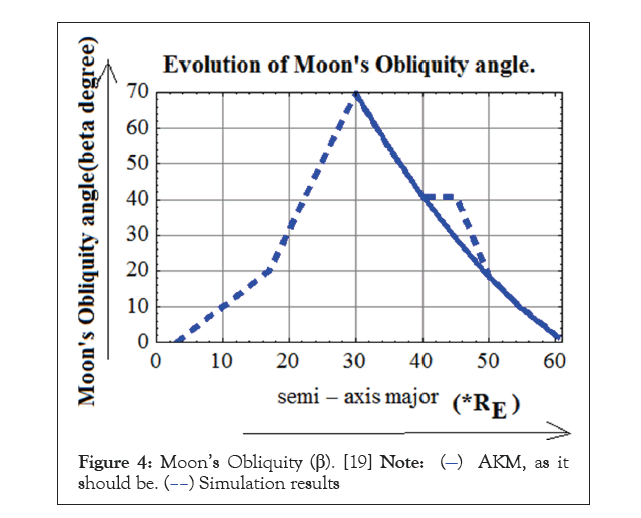
Figure 4: Moon’s Obliquity (β). [19] Note:

Discussion

Summing up the findings made by Cuk et al. [19] and by this paper we see the following:

Inspection of Table 3 leads us to a definite conundrum. After Cassini State 2 is reached, Earth-Moon system enters angular momentum conservative phase. If lunar obliquity tides generated by Cassini state transition help reduce inclination angle from 27.54° to 5.14°. Then by necessity of angular momentum conservation, obliquity must increase. This implies that current obliquity of 23.44° can be achieved only if obliquity angle is zero after Cassini State Transition.

Table 3: Four stages in tidal evalution of E-M system

This is obvious by the inspection of Figures 2-4. As we see Figures 3 and 4 give a continuity between AKM results and Simulation results in the evolution of inclination and Moon’s obliquity data. The two results smoothly merge. But Figure 2 shows a discontinuity near 40 R_E for Earth’s obliquity. To achieve 23.44° modern value of Earth’s obliquity the Earth Moon system must achieve 0° Earth’s obliquity just earlier than 40 R_E when Moon settles down in Cassini state 2. Since angular momentum conservation is not required from Laplace Plane Transition to Cassini State Transition it is quite possible that strong obliquity tides are reducing inclination angle as well as Obliquity angle. Then only the climate friendly low obliquity can be achieved. At this point, Cuk et al. [19] are completely quiet. This is a definite conundrum which needs to be addressed before we can assert that “Our tidal evolutionary model supports high angular momentum, giant impact scenario to explain Moon’s isotopic composition and provide a new pathway to reach Earth’s climatically favourable low obliquity.”

Conclusion

This paper brings kinematic model renamed as Advanced Kinematic Model (AKM) of tidally interacting binaries to a new level of maturity whereby it will prove to be more effective in dealing with real life scenario. There is dramatic improvement in the correlation of new model and the real world. In Determination of J4 vector=J2 vector+J3 vector=Total AM of E-M system an assumption has been made that: in Figure 1, interior angle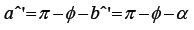

How valid is this assumption over the entire permissible range (40 R_E to 60.33 R_E) of AKM will have to be critically examined in a sequel paper. Cuk Muteja et al. have proposed that Earth-Moon system while passing through Laplace plane transition and Cassini state transition pass through chaotic and turbulent phase and due to strong obliquity tides in Moon the tidal evolution gets stalled or even reversed for long periods of its existence. E-M system moves in ‘Fits’ from 3 RE to 17 R_E and subsequently to 51.4 RE in 3.267 Gy and then it ‘Bounds’ from 51.4 R_E to 60.33 R_E in 1.2 Gy.

At 17 R_E Laplace plane transition occurs and at 33 R_E Cassini state transition occurs. Cuk Matija have assumed that Moon is born from the Giant impact generated debris disk when Mars sized planetesimal made a glancing angle collision with proto Earth resulting in high obliquity and high Angular Momentum Earth. This resulted in isotopic identity of wide range of materials on Earth and Moon and the subsequent tidal evolution resulted in achieving climatically favorable Earth’s obliquity of 23.44°. The application of AKM to this Fits and Bound model of E-M system gives a theoretical LOD curve which has precise match with observed LOD curve over last 1.2 Gy as shown in Supplementary S6 using the Protocol Exchange algorithm http://org.1038/protex.2019.017. In addition all the observed performance parameters are theoretically justified. The observed parameters are LOD=24 h, LOM/LOD=27.32 and velocity of recession of Moon as 3.82 ± 0,07 cm/y all these are a natural corollary of AKM. Using the Protocol Exchange algorithim in Supplementary S6 AKM is vindicated on every count. In effect AKM has helped arrive at the correct theoretical formalism of Observed LOD curve. This theoretical formalism will give the datum against which the real time fluctuations in LOD will be compared and the precursors of the impending Earth-quake and sudden volcanic eruptions will be identified and used to give Early Warning and Forecasting for terrestrial disasters triggered by plate tectonic movements (Shown in S7 of Supplementary file).

Acknowledgments

This continued research in E-M system has been made possible under Emeritus Fellowship Scheme sponsored by University Grants Commission, India. The Grant number is EMERITUS/2012-13-GEN-855/. I acknowledge the cooperation extended by the Director, IIT Patna for letting me use the resources at the central Library of the Institute. I acknowledge the cooperation extended by Prof. Pramod Kumar Mishra and Prof Pritam Kumar in EE Department, IIT Patna, for the use of their e-resources. In preparation of this paper. I also acknowledge the cooperation extended by the Director of NIT, Patna, as well as HOD, Electronics and Communication Department, NIT, Patna, in their continued support of my ongoing Research Programme in both Electronics and in Celestial mechanics.

Conflict of Interest

I have no conflict of interest financial or otherwise whatsoever with anybody.

Author Contributory Statement

Author collected the data regarding Length Of Day (LOD) in past epoch from popular science books of Issac Asimov and Carl Sagan (COSMOS). After receiving the Press Release of NASA on the silver jubilee anniversary of Man’s landing on Moon (Moon had receded by 1m in 25years) Author redid the analysis of E-M system and presented it at 82nd Session of Indian Science Congress at Jadavpur University, Kolota in 1995.. The Author further elaborated the E-M System model and presented the Kinematic Model of E-M system at World Space Congress, Houston, in 2002. In 2004 at 35th Scientific Assembly at Paris Kinematic Model was extended to Solar System and a new perspective on birth and evolution of our Solar System and exoplanetry system was presented. In 2012 at 39th Scientific Assembly of COSPAR at in 2012 at Mysore, India paper B03-0011-12 “Iapetus hypothetical sub satellite revisited and it reveals celestial body formation in Primary Centric Framework”. In 2017 at CELMEC VII held at Viterbo, Rome, the present paper on Advanced Kinematic Model was presented. Subsequent to this a sequel paper titled “The Past, Present and the Future of Earth Moon Orbital Globe Dynamics and its Habitability” was published in Journal of Mathematical Techniques and Computatioal Methods 2(1), 48-66, 2023.

Data Availability

All the data are available within this paper.

Dedication

This paper is dedicated to --“An Indian Spacecraft has become the first to land near the Moon’s rock and crater strewn South Pole, making the country the World’s fourth to perform a controlled landing on body”, Padma, J.V. “ India lands on Moon ! Scientists celebrate as Chandrayaan-3 touches down”, Nature, Volume 620, Issue 7975, 24th August 2023.

References

1. Darwin GH. XIII. On the precession of a viscous spheroid, and on the remote history of the Earth. Philos Trans R Soc. 1879;170:447-538.

   [Crossref] [Google Scholar]

2. Darwin GH. XX. On the secular changes in the elements of the orbit of a satellite revolving about a tidally distorted planet. Philos Trans R Soc. 1880;171:713-891.

   [Crossref] [Google Scholar]

3. Stephenson FR, Houlden MA. Atlas of Historical Eclipse Maps: East Asia 1500 BC-AD 1900. Cambri Univer Press. 1986.

   [Google Scholar]

4. Stephenson FR. Historical eclipses and Earth's rotation. Astron Geophys. 2003;44(2):2.22-2.27.

   [Crossref] [Google Scholar]

5. Morrison LV. Tidal Deceleration of the Earth’s Rotation Deduced from Astronomical Observations in the Period A D. 1600 to the Present. Tidal Frict Earth’s Rotat. 1978:22-27.

   [Google Scholar]

6. de Jong T, van Soldt WH. The earliest known solar eclipse record redated. Nature. 1989;338(6212):238-240.

   [Google Scholar]

7. Sharma BK, Ishwar B, Rangesh N. Simulation software for the spiral trajectory of our Moon. Adv Space Res. 2009;43(3):460-466.

   [Crossref] [Google Scholar]

8. Sharma BK. The Architectural Design Rules of Solar Systems Based on the New Perspective. Ear Moon Plan. 2011;108:15-37.

   [Crossref] [Google Scholar]

9. Krasinsky GA. Dynamical history of the Earth–Moon system. Celest Mech Dyn Astron. 2002;84:27-55.

   [Crossref] [Google Scholar]

10. Stevenson DJ. A planetary perspective on the deep Earth. Nature. 2008;451(7176):261-265.

    [Google Scholar]

11. Touboul M, Kleine T, Bourdon B, Palme H, Wieler R. Late formation and prolonged differentiation of the Moon inferred from W isotopes in lunar metals. Nature. 2007;450(7173):1206-1209.

    [Google Scholar]

12. Wells JW. Coral growth and geochronometry. Nature. 1963;197:948-950.

    [Google Scholar]

13. Coughenour CL, Archer AW, Lacovara KJ. Tides, tidalites, and secular changes in the Earth–Moon system. Earth-Sci Rev. 2009;97(1-4):59-79.

    [Crossref] [Google Scholar]

14. Stephenson FR, Morrison LV, Smith FT. Long-term fluctuations in the Earth’s rotation: 700 BC to AD 1990. Philos Trans R Soc. 1995;351(1695):165-202.

    [Crossref] [Google Scholar]

15. Lambeck K. The Earth's variable rotation: geophysical causes and consequences. Cambridge University Press. 2005.

    [Google Scholar]

16. Kant I. Whether the Earth has undergone an alteration of its axial rotation (Translated), Universal Natural History 1969. Univers Michigan Press. 1754:1-11

    [Google Scholar]

17. Ida S, Canup RM, Stewart GR. Lunar accretion from an impact-generated disk. Nature. 1997;389(6649):353-357.

    [Google Scholar]

18. Kagan BA. Earth—Moon tidal evolution: model results and observational evidence. Prog Oceanogr. 1997;40(1-4):109-124.

    [Crossref] [Google Scholar]

19. Ćuk M, Hamilton DP, Lock SJ, Stewart ST. Tidal evolution of the Moon from a high-obliquity, high-angular-momentum Earth. Nature. 2016;539(7629):402-406.

    [Google Scholar]

20. Canup RM, Asphaug E. Origin of the Moon in a giant impact near the end of the Earth's formation. Nature. 2001;412(6848):708-712.

    [Crossref] [Google Scholar]

21. Burkhardt C. Isotopic Composition of the Moon and the Lunar Isotopic Crisis. Encycl Lunar Scie. 2015:1-13.

    [Crossref] [Google Scholar]

22. Young ED, Kohl IE, Warren PH, Rubie DC, Jacobson SA, Morbidelli A. Oxygen isotopic evidence for vigorous mixing during the Moon-forming giant impact. Scien. 2016;351(6272):493-496.

    [Crossref] [Google Scholar]

23. Nicholson PD, Cuk M, Sheppard SS, Nesvorný D, Johnson TV. Irregular satellites of the giant planets. Solar Sys Bey Neptune. 2008;411.

    [Google Scholar]

24. Atobe K, Ida S. Obliquity evolution of extrasolar terrestrial planets. Icarus. 2007;188(1):1-17.

    [Crossref] [Google Scholar]

25. Keane JT, Matsuyama I. Evidence for lunar true polar wander and a past low‐eccentricity, synchronous lunar orbit. Geophys Res Lett. 2014;41(19):6610-6619.

    [Crossref] [Google Scholar]

26. Ward WR. Past orientation of the lunar spin axis. Scien. 1975;189(4200):377-379.

    [Crossref] [Google Scholar]

27. Chyba CF, Jankowski DG, Nicholson PD. Tidal evolution in the Neptune-Triton system. Astron Astrophys. 1989;219:L23-L26.

    [Google Scholar]

28. Rubincam DP. Tidal friction in the Earth–Moon system and Laplace planes: Darwin redux. Icarus. 2016;266:24-43.

    [Crossref] [Google Scholar]

29. Rubincam DP. The obliquity of Mars and “climate friction”. J Geophys Res Planets. 1993;98(E6):10827-10832.

    [Crossref] [Google Scholar]