Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2017) Volume 10, Issue 2
MicroRNAs are small, non-coding RNA molecules that regulate gene expression. MicroRNA may binds to mRNAs and control the intended function of mRNAs. There are a handful of computational algorithms for target prediction, but the degree of false positives and false negatives are high. In this paper, we propose a Hidden Markov Model for seed prediction and a Support Vector Machine (SVM) classifier for target prediction. Positive data set for training has been collected from experimentally validated targets, while negative data set has been identified systematically from predicted false positives. Each mRNA target candidate sequence is aligned with microRNA sequence and tested for a seed region using the trained HMM model. If the test succeeds, 22 features were extracted from the aligned duplex and fed into an SVM classifier. HMM based seed identification module works with an accuracy of 95.6% and SVM classifier provides 97.49% accuracy. We have compared binding sites of 9 microRNA in 148 m RNAs with the results of validated target sites and our results are more accurate than other approaches.
Keywords: MicroRNA; Binding sites; Hidden markov models; SVM classifiers
HMM: Hidden Markov Model; SVM: Support Vector Machines
MicroRNAs are the group of single stranded non-coding RNAs of 24-31 nucleotides length which play very important role in gene regulation. They bind with protein coding genes (mRNAs) and may cause either a repressed translation or mRNA decay [1,2]. Thus, the intended function of mRNA may get affected and can lead to progression/suppression of several diseases. At present, sufficient and strong evidences are available for its regulatory role in human diseases such as neurological disorders, cardiac problems and many versions of cancer [3].
The location where microRNA gets attached with mRNA is called binding site or target site. To design a powerful tool to study the biology of diseases connected with microRNAs, pathways that are associated with the prognosis/progression of diseases are indispensable. Experimental identification of microRNA binding sites is time consuming due to low expression of microRNAs, tissue specificity and procedural delay of experiments. Computational approaches have been extensively used in microRNA research to identify most probable candidate sites. A number of algorithms and techniques have been developed for microRNA prediction and its target identification [4]. Still, there is a demand for new approaches and algorithms that give better results in predicting target sites than existing ones. MicroRNA target finding is a challenging task especially in the case of animals, due to the complexity as well as the limited knowledge of exact rules governing the interaction of microRNA with mRNA. Most of the computational algorithms rely on a database of experimentally validated microRNA-mRNA interactions and properties related to the interaction. These properties can be categorized into different groups such as structural, base pairing, thermodynamic and positional properties. In the duplex structure, a segment of size 7 or 8 with majority of Watson-Crick base pairs at 5’ end of microRNA is called seed region. This is the most evolutionary conserved region. A number of studies emphasized the importance of seed region [5-7]. There are minor differences in the definition of seed region among the tools. MirTarget 27 defines four types of seeds based on the number and the position of nucleotides in the region: from 1 to 8, 1 to 7, 2 to 8 and 2 to 7. A comparative study of mRNA down regulation by each category of seed region was conducted in mirTarget2. PicTar6 considered seed as a Watson-Crick base paired stretch of 7 nts starting at 1st or 2nd position and no wobble pairing was allowed. But, mutation/insertions in seed region are allowed, provided the free energy level does not increase. Based on base pairing, targets can be divided into three groups, namely 5’ dominant seed only targets, 5’ dominant canonical targets, and the 3’ complimentary targets [8]. In the cases of 5’ dominant canonical and 3’ complimentary targets, mismatches in seed region are compensated by additional base pairing at 3’ end.
Thermodynamic stability of microRNA: mRNA duplex is used as a distinguishing feature in majority of tools. The minimum free energy or Gibb’s free energy (Δtt) shows the stability of a structure formed by bio-molecules. To ensure a stable structure, Δtt of folded nucleic acid structure needs to be the lowest. RNA hybrid predicts targets by finding most favorable hybridization energy of small RNA with an mRNA molecule [9]. When hybridization energy is computed, base pairing between target nucleotides or between microRNA nucleotides are not allowed to avoid intra-molecular hybridizations. In algorithmic point of view, RNA hybrid is an extension of classical RNA secondary structure prediction technique.
Among the algorithms MiRanda, [10] TargetScan, [11] PicTar [6] and MTar [8] used a test for conserved regions as the initial screening step in the process of target prediction, whereas RNA22 [12] MicroTar [13] and TargetSpy [14] have considered factors other than conservation during this step. TargetScan, miRanda and PicTar perform an extensive search in the 3’ UTR of mRNAs for probable targets. PicTar perform multiple sequence alignment of 3’ untranslated (3’UTR) segments, then search for co-expressed mature microRNA sequence and further filtered with seed conservation and minimum free energy. Its false positive rate has been estimated to be around 30%. TargetScan search for conserved seed match (positions from 2 to 7) of the microRNA in 3’ UTRs of five genomes (human, rat, dog, mouse and chicken).
TargetSpy is not relying on evolutionary constraints and hence not looking for the presence of a seed match. It uses machine learning approach with 35 structural, thermodynamic and positional features extracted from known target sites. Initial screenings of candidate targets is done by searching for areas in target sequence where predicted free energy is below a threshold value.
Researchers turned their attention to develop tools that employ a number of target finding programs to get a better result than what they could individually attain. One such tool is comiR [15], a support vector machine based tool, where a single probabilistic score is computed from an ensemble of four microRNA target prediction algorithms, namely PITA [16], miRanda, TargetScan and mirSVR.
Due to the advancement of Next Generation Sequencing (NGS), microRNA expression profiling studies get accelerated and a huge number of expressions based down regulation mRNA cell lines are being investigated [17]. MtiBase is NGS based approach, particularly exploring the microRNA binding sites in coding sequences (CDS) and 5’ untranslated (5’UTR) regions of mRNAs, instead of search limited to conventional 3’UTR regions [18].
Comparative studies in analyzing the performance of different target prediction tools show demand for new prediction algorithm. The first major study in prediction accuracy of target finding algorithms was conducted by Sethupathy et al. [19] Experimentally validated target sites from a well-known database, Tarbase [20] were used to verify the predicted targets and hence to find sensitivity and specificity of prediction algorithms. According to this study, the sensitivity of MiRanda was 49% and that of TargetScanS and PicTar was 48% each. This approach had a limitation that the number of validated target sites at the time of study was limited and hence their findings were unjustified to some extent. Another approach used to validate the authenticity of targets predicted by algorithms is to investigate the effect of microRNA over expression in protein production. Stable Isotope Labeling with Amino acids in Cell culture (SILAC) is a technique that finds difference in protein abundance. Baek et al. applied SILAC method to compare results of target finding algorithms (in vivo with in silica) with protein production and reported that TargetScan and PicTar were giving good performances [21]. Alexiou et al. used a modified SILAC approach to study protein production effect on over expression of five microRNAs (miR-1, miR-16, miR-3a, miR-155 and let-7b) and reported that precision of predicted targets was 51%, 48% and 49% for the tools TargetScan, DIANA-microT and PicTar, respectively [22]. TargetMiner is a classifier for target prediction trained with negative samples prepared by systematic identification from the false positive targets. They compared their results with predicted targets of 10 different algorithms in terms of specificity, sensitivity and accuracy and reports that accuracy of target prediction tools is still around 70% [23].
Earlier, there were difficulties in using machine learning for target prediction as sufficient numbers of validated targets were not available [20]. At present, information about a large number of genes that have up/ down regulation due to microRNA interactions is available. MirTarBase, a database of microRNA: An mRNA interaction contains details of more than 0.3 million records, between 2619 microRNAs and 14884 genes. Among these target interactions, the interactions validated by experimental methods such as Western Blot, Luciferase assay are only 3527 and 5081, respectively. The remaining vast majority are from NGS experiments. Similarly, another database, MI Records contains 2112 interactions between 1106 genes and 304 microRNAs. On a detailed analysis, information about only 585 binding sites (exact locations) is available. The increased data availability and high false positive rates of the presently available algorithms demand development of new algorithms. In this paper, we present an HMM based seed prediction followed by Support Vector Machine (SVM) based binding site prediction system for microRNA target sites.
Data collection
Sufficient collections of positive and negative data samples are indispensable for effective machine learning. Positive data samples were collected from validated targets sites published in databases such as miRecords [24] and mirTarbase [25]. Randomly generated negative samples might be giving best results in cross validation, but may fail to repeat the same performance in real test cases. The higher rate of false positives in target prediction is due to the close resemblance of real targets with the non-targets. Bandyopadhyay et al. suggested a method for systematic identification of negative samples [23]. We have adopted Bandyopadhyay’s model with a modification for negative sample preparation. Initial negative data set was prepared by choosing binding sites predicted by utmost one of the target finding tools- MiRanda, TargetScanS, PicTar or RNA22. This was further filtered by applying random sub sampling of two positions in the seed region, followed by a test for cut off energy. Lower accessibility energy (ΔΔG) indicates a higher chance of being a target.
It is calculated as, ΔΔG = Δduple− Δopen, Where Δopen is energy needed to make a target region accessible to microRNA and Δduplex is the energy of the microRNA: mRNA duplex. We select instances where ΔΔG ≥ 0 as negative samples.
Our data set consists of 404 positive and 434 negative samples. On analysis, it is found that the average length of binding sites in mRNA sequences is 23 base pairs.
Hidden markov model
Hidden Markov Model (HMM) is a statistical model used in pattern recognition. In HMM, the system being modeled consists of a set of hidden states, a set of visible states and undergoes a Markov process. Hidden states are non-observable states. On every input symbol, a state may transit to another state or retain in the same state, but emits a visible symbol. Thus, two different probabilities, a transition probability and an emission probability came into the picture. Transition probability (aij) is the probability of transition from a state ωi at (t − 1)th instant of time to another state ωj at tth instant of time. The sum of transition probabilities from any state is 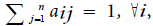 where n is total number of hidden states. Emission probability (bjk) is the probability of emitting a visible symbol vk from a state wj, and
where n is total number of hidden states. Emission probability (bjk) is the probability of emitting a visible symbol vk from a state wj, and 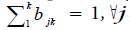 , where k is the number of visible symbols from a state. Given an HMM model (θ) defined by set of hidden states ωn, visible states vk, transition probabilities aij and emission probabilities bjk, then P(vT|θ) is the probability of a sequence vT generated from the model θ, where T is the length of sequence. P (vT|θ) is calculated by repeatedly by computing the term αj (t) by using the forward algorithm. αj (t) is the probability that machine is in state wj at an instant of time t after emitting t number of symbols.
, where k is the number of visible symbols from a state. Given an HMM model (θ) defined by set of hidden states ωn, visible states vk, transition probabilities aij and emission probabilities bjk, then P(vT|θ) is the probability of a sequence vT generated from the model θ, where T is the length of sequence. P (vT|θ) is calculated by repeatedly by computing the term αj (t) by using the forward algorithm. αj (t) is the probability that machine is in state wj at an instant of time t after emitting t number of symbols.
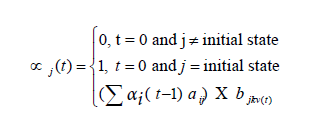
Where 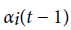 is value of at (t − 1)th instant of time. P (vT|θ) is calculated as the value of
is value of at (t − 1)th instant of time. P (vT|θ) is calculated as the value of 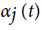 at t = T.
at t = T.
Given a sequence of visible symbols 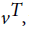 the probability that sequence emitted from a model is given by
the probability that sequence emitted from a model is given by 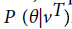 . This can be computed as
. This can be computed as 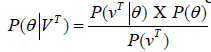 . To develop a classifier based on HMM, separate models need to be created with respect to the classes. Assume
. To develop a classifier based on HMM, separate models need to be created with respect to the classes. Assume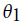 and
and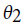 are two HMM models. For a given visible state sequence
are two HMM models. For a given visible state sequence 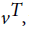 if
if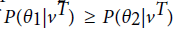 then we could conclude that vT belongs to the class
then we could conclude that vT belongs to the class 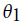 , otherwise to the class
, otherwise to the class 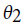 .
.
A general scheme for microRNA binding site prediction is shown in Figure 1. The proposed system consists of a windowing mechanism, a sequence alignment module, a HMM module and a SVM classifier. This system accepts a mRNA sequence and a microRNA sequence as inputs. The windowing mechanism extracts a candidate binding site of size 25 nucleotides from the mRNA sequence. This sequence is aligned with the microRNA sequence using Smith-Waterman algorithm and tested for seed match using the trained HMM model. If a match is detected, 22 features are extracted from the aligned duplex. A feature vector consists of 23 parameters (including HMM Score) is tested for a valid target with the trained SVM classifier. If HMM test is failed initially, next candidate sequence is fetched. This process continues until the end of mRNA sequence. The step size of windowing technique is fixed at 3. The reason to keep step size as 3 is to examine every 3rd possible subsequence (candidate sequences) and thus not miss a potential binding site. For a given mRNA sequence of length n, the number of candidate sequences generated is (n-25)/3. The advantage of HMM model is the initial identification and elimination of probably non target regions without conducting computationally expensive feature extraction process.
HMM model for seed prediction
The HMM model designed for seed prediction is depicted in Figure 2. WC1 and WC2 are the states that correspond to Watson Crick (WC) pairs- GC, CG and AU, UA respectively. We choose separate states for each WC base pairs, so as to capture the sequence order of base pairs in the seed region. A third state is Wobble state (WB) and all other input conditions are treated as a mismatch and represented as a state, W/M. The model corresponding to the positive samples (Seed class) is named as TrueHMM and that of negative samples (NonSeed class) is named as FalseHMM.
Table 1 shows the states and possible symbols emitted from each state. The first three states have only two symbols to emit, but 18 different symbols are emitted from the state W/M.
| States | Possible Emissions |
|---|---|
| WC1 | GC, CG |
| WC2 | AU, UA |
| WB | GU, UG |
| W/M | AA, CC, GG, UU, AG, GA, CA, AC, UC, CU, A-, G-, C-, U-, -A, -G, -C, -U |
Table 1: HMM States with possible symbol emissions.
Initial values of transition and emission probabilities are calculated as follows:

Training data sets for the HMM model are the seed regions extracted from 330 positive and 350 negative samples of the data collected as per the method described in the section 2.1. P (seed|θ) is calculated by repeated computation of αj (t) as many times as the length of seed:
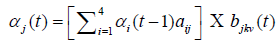
At each instant of time, αj (t) is calculated as sum of products of its previous value αi(t−1) and values of emission and transition probabilities from four different states. αj (t) values are computed with respect to the models, TrueHMM and FalseHMM. The function max (P (TrueHMM|vT), P (FalseHMM|vT)) decides the class to which V T belongs.
Feature extraction: The prospects of an application which employs machine learning are determined by the feature extraction and the feature selection method. Features used in this study are summarized in Table 2. MicroRNA binds to a target mRNA sequence and forms a duplex structure. We used Smith-Waterman algorithm to obtain an optimal alignment between the sequences. This is a dynamic programming based algorithm. We defined a scoring matrix (Si,j), with score value for every possible base pairs. As the required alignment is complementary base pairing, we assigned score values as follows: G-C and A-U as 5, G-U as 2 and others as -3. Another matrix Mi,j, 0 ≤ i ≤ m, 0 ≤ j ≤ n where m and n are length of sequences to be aligned, is the crux of the algorithm. Each Mi,j value is computed using adjacent cell values, a score value Si,j and a gap penalty w.
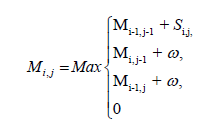
| Sl. No. | Properties | Description |
|---|---|---|
| 1 | Stretch Length | Number of consecutive base pairs in the duplex |
| 2 | HMM Score | Negative log value of HMM Score of seed region |
| 3 | Score Duplex | The total score calculated as sum of product of the weight (w) and the corresponding pair score. Seed region w=2, non-seed region w=1 |
| 4 | Seed Score | Seed Score: Sum of base pair scores in the seed region. G:C and A:U with 5, G:U with 2 and the others with -3 |
| 5 | Free Energy of duplex | Free Energy of the duplex, calculated using RNAfold |
| 6 | WC Count | Number of G-C, A-U base pairs |
| 7 | U Frequency Ratio | Ratio between frequency of U and length of target sequence |
| 8 | G Frequency Ratio | Ratio between frequency of G and length of target sequence |
| 9 | A Frequency Ratio | Ratio between frequency of A and length of target sequence |
| 10 | Wobble Count | Number of Wobble pairs in the duplex(G-U) |
| 11 | C Frequency Ratio | Ratio between frequency of C and length of target sequence |
| 12 | Di-nucleotide Ratio | Ratio of di-nucleotides in the microRNA and in the target sites. There are 16 possible di-nucleotides (AA, AC, AU, ..UU), so 16 different attributes |
| 13 | mRNA Bulge2 | Number of bulges on the target site of size 2 |
| 14 | mRNA Bulge3 | Number of bulges on the target site of size 3 |
| 15 | Rest of Seed Score | Sum of pair scores in a non-seed region. G:C and A:U with 5,G:U with 2 and the others with -3 |
| 16 | Free Energy of mRNA | Free energy of the target sequence, calculated using RNA fold |
| 17 | Duplex Bulges | Number of bulges in the duplex |
| 18 | Total Mismatch | Number of mismatches in duplex |
| 19 | Length microRNA Bulge | Length of largest bulge in the duplex |
Table 2: List of features and their descriptions.
Complexity of this algorithm is O(mn). A local optimal alignment between the given mRNA (5’-3’) and microRNA (3’-5’) is obtained by a trace back from the highest valued cell in the nth row to a 0 value in the matrix (Mn,m). In this experiment, region from 2nd to 8th of the aligned duplex from the 5’ end of microRNA is treated as the seed region.
A probability value P (θ|vT), where vTis the seed region is computed from the TrueHMM model is included in the feature vector in a different way. This feature is named as HMM Score, which is computed as negative logarithmic value of P (θ|vT). A total score value from the entire duplex is chosen as another feature. This is calculated as the weighted sum of score values of the pairs in the duplex, with a weight assigned to seed region as twice as that of non-seed region. Other features chosen are free energy value of duplex as well as that of individual sequences. A dynamic programming based algorithm, RNAFold [26] is used to compute the free energy of a sequence. Base compositions of four single nucleotides and 16 dinucleotides(AA, AC, ...TT) are taken as features, and thus the feature vector contains 33 attributes.
Support vector machine based classifier model: A model with Support Vector Machine (SVM) as the classifier has been built to identify microRNA binding sites. A linear SVM classifier is based on discriminant function of the form f (x) = ωT x + b, where ω is weight vector, x is input vector and b is bias. The set of all points with ωT = 0 define a hyperplane. SVM starts with initial random values for ω and b. During the training phase, for every sample xi belonging to the class C1, whether ωT xi + b > 0 is tested. If not, ω and b values are modified so that xi is moved to the positive side of hyper plane. Similarly for instances belonging to class C2, values of ω and b are adjusted. The closest points to the hyperplane among positive and negative samples define margins. Thus SVM is an optimization problem, so as to maximizing the margin between the data points, subjected to following constraints:
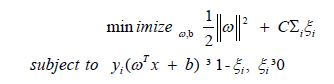
The term, 0 ≤ ξi ≤ 1, define penalty for margin error. A nonlinear SVM works projecting the data points in the input space to a feature space of higher dimension. This can be represented as a function of the form f (x) = ωT φ(x) + b, where φ is a non-linear function. To limit the size of feature space and thus to restrict the memory as well as the computational requirements, a method known as kernel trick k is employed, rather than a direct computation of the mapping function φ. There are several different kernel functions. A polynomial kernel is k(x, y) = (xT y + 1)d where d is the degree of polynomial.
The classifier model has been evaluated with 10 fold cross validation and independent test set. When experiments repeated with different nonlinear kernel functions, polynomial kernel was giving the best performance. Different performance measures computed are the following:
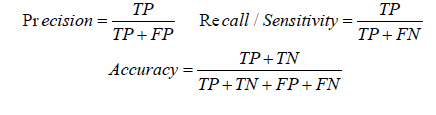
Analysis of HMM model
MicroRNA binding site prediction with an initial lookup using an HMM model is one of the first works reported in this domain. TrueHMM has been trained with seed regions (2nd to 8th positions) of 330 positive samples whereas FalseHMM has been trained with 350 negative samples. Remaining positive and negative samples are used to evaluate performance of the model. Training, in effect computes the transition and the emission probabilities. We used Baum-Welch algorithm to fine tune the values of emission and transition probabilities estimated using the equations defined in section
Baum-Welch algorithm is a modified expectation-maximization algorithm, which repeatedly estimates the model parameters by applying forward and backward algorithms [27]. Table 3 shows the matrix of transition probabilities obtained from the training sets.
| WC1 | WC2 | WB | W/M | WC1 | WC2 | WB | W/M | |
|---|---|---|---|---|---|---|---|---|
| WC1 | 0.4157 | 0.4357 | 0.0986 | 0.0487 | 0.3189 | 0.3478 | 0.218 | 0.1153 |
| WC2 | 0.4328 | 0.3968 | 0.1065 | 0.0639 | 0.336 | 0.2883 | 0.2008 | 0.175 |
| WB | 0.4546 | 0.3939 | 0.0707 | 0.0808 | 0.2821 | 0.3077 | 0.2251 | 0.1852 |
| W/M | 0.3758 | 0.3289 | 0.1007 | 0.1946 | 0.2532 | 0.2046 | 0.2558 | 0.2865 |
Table 3: Transition probabilities left side of the table shows transition probabilities obtained from the seed regions of positive samples. Right side of the table shows the values from seed regions of negative samples.
Figure 3 shows seed identification of typical microRNA: mRNA pair using the trained model. At each instant of time, the state that emits the required symbol with highest probability is marked with a circle. As an example, for a sample microRNA: mRNA pair shown in Figure 3, at any instant of time t, the probability value (αj (t)) with respect to the fragment of sequence upto tthof time, is computed using the method described in the section 2.2. In this example, at 7th instant of time, TrueHMM model gives probability value as 3.1799E − 06 whereas FalseHMM model gives value as 2.22027E − 06. These values result in a positive seed prediction for the given sample.
When 74 positive and 84 negative samples were tested with the HMM model, 70 positive instances and 81 negative instances were predicted correctly. Thus the accuracy of seed prediction is 95.6%, precision is 0.959 and recall rate is 0.956 as shown in Table 4.
| TP | TN | FP | FN | Precison | Recall | Accuracy |
|---|---|---|---|---|---|---|
| 70 | 81 | 3 | 4 | 0.959 | 0.946 | 0.956 |
Table 4: HMM seed predictor: performance measures.
Analysis of binding site prediction model
We have developed a binding site prediction model using SVM classifier with polynomial kernel. This model is trained and tested using 404 positive and 434 negative instances of microRNA: mRNA interactions. A total of 33 features were extracted. We have ranked the features based on their decisive power as measured by information gain of each attribute. Table 5 shows the result obtained when the experiments were conducted by 10 fold cross validation with varying number of features. When 23 top ranked features were used, the prediction accuracy obtained was 97.49%. There was no further increase in accuracy when more features were included. With the same 23 features, precision obtained was 0.995, which shows the presence of false positives in the output is negligibly small. Here, among 387 instances predicted as targets only 2 were wrongly chosen. But at the same time, recall value obtained was only 0.953, as 19 instances of true targets were wrongly predicted as non targets. When 6 more features related to the complementary structure formed by microRNA:mRNA duplex were removed, there was no exorbitant decrease in measures, prediction accuracy kept it value at 94.98% and precision at 0.962 and recall at 0.933. When experiment was conducted with most significant 10 features, 92.36% instances were classified correctly.
| Test Method | TP | TN | FP | FN | Preci- sion |
Recall | F-Mea- sure |
Accuracy |
|---|---|---|---|---|---|---|---|---|
| 10 fold CV 23 attributes |
385 | 432 | 2 | 19 | 0.995 | 0.953 | 0.974 | 97.49 |
| 10 fold CV 20 attributes |
383 | 421 | 13 | 21 | 0.96 | 0.959 | 0.959 | 95.49 |
| 10 fold CV 17 attributes |
377 | 419 | 15 | 27 | 0.950 | 0.950 | 0.950 | 94.98 |
| 10 fold CV 10 attributes |
365 | 409 | 25 | 39 | 0.917 | 0.916 | 0.916 | 92.39 |
Table 5: Validation of SVM classifier for binding site prediction with 10 folds cross validation.
Further validation of the developed system has been done with independent test set. When 125 positive and 160 negative instances were tested against the trained model, the numbers of wrong predictions were only 10. Table 6 shows result from the classifier model when independent test sets were employed.
| Test Method | TP | TN | FP | FN | Preci- sion |
Recall | F-Mea- sure |
Accuracy |
|---|---|---|---|---|---|---|---|---|
| Independent data set P-125, N-160 |
117 | 158 | 2 | 8 | 0.983 | 0.936 | 0.965 | 96.49 |
Table 6: Validation of SVM classifier for binding site prediction with independent test set.
Feature selection is the process of selecting a subset of features so as to provide maximum performance with minimum resources such as storage and computational time. In this study, feature selection was made based on information gain of each attribute. On analysis, it was found that HMMScore is the most influential attribute in this model. HMMScore was computed as −log(p), where p is the difference in probability values for a seed region, after all state transitions were completed in the TrueHMM and FalseHMM models. The second deciding parameter in our study was free energy of microRNA: mRNA duplex. Top ranked 10 attributes are shown Table 7.
| Rank | Attribute |
|---|---|
| 1 | HmmScore |
| 2 | EnergyDuplex |
| 3 | TotalPositionalScore |
| 4 | TotalNoWC |
| 5 | AUcontentRatio |
| 6 | SeedScore |
| 7 | GCcontentRatio |
| 8 | ApropCount |
| 9 | UpropCount |
| 10 | CpropCount |
Table 7: Top 10 attributes of the Binding site prediction model.
Figure 4 shows differences in accuracy and precision when five, ten, seventeen and twenty three features were used for prediction. With ten features, there were 25 cases of non-targets predicted as targets, and with 5 features this value was increased to 60.
Figure 5 shows ROC curves when varying number of attributes were employed. When 23 attributes were used, True Positive Rate (TPR) reached a high value of 0.9527 while False Positive Rate (FPR) was as low as 0.0046. With just 5 attributes, TPR touched 0.8539 when FPR was at 0.112.
We have a handful of tools available for computational prediction of microRNA binding sites in mRNAs. Wide range of techniques such as machine learning, rule based methods and pattern recognition were employed in these tools. Properties of microRNA: mRNA interactions such as thermodynamic stability, structural, positional features and evolutionary conservation were taken into consideration. Also, there are public databases showing experimentally validated interactions as well as predicted interactions. We used one such database, namely miRecords to validate the accuracy of our predictions. miRecords keeps track of experimentally validated interactions and the status of predictions for the same interactions by other popular tools. Though the binding locations were different, these tools predict 50 -70 % of validated interactions successfully. Table 8 shows a comparison of MTar2 with other popular tools in terms of number of validated target predictions. In the case of hsa-let-7a, there were 23 validated targets, out of which 9 targets were predicted by PITA and RNAhybrid. Results from MTar2 are either in par with or above than that of most popular tools. A detailed list of predicted targets by MTar2 is given as supplementary file.
| Micro RNA | Validated Targets |
miR and a | Mir- Target2 Pic |
Pic- Tar |
PITA | RNA Hybrid |
Target Scan S |
MTar | MTar2 |
|---|---|---|---|---|---|---|---|---|---|
| hsa-let-7a | 23 | 9 | 4 | 5 | 9 | 9 | 5 | 5 | 9 |
| hsa-miR- 126 |
8 | 4 | 0 | 1 | 3 | 5 | 1 | 2 | 4 |
| hsa-miR- 221 |
20 | 2 | 0 | 3 | 3 | 3 | 3 | 2 | 3 |
| has-miR- 133a |
9 | 0 | 0 | 1 | 3 | 6 | 0 | 2 | 6 |
| hsa-mir- 181c |
5 | 1 | 2 | 1 | 1 | 2 | 0 | 1 | 3 |
| hsa-mir- 181b |
10 | 4 | 4 | 2 | 4 | 5 | 2 | 3 | 6 |
| hsa-mir- 21 |
40 | 16 | 14 | 9 | 22 | 24 | 9 | 14 | 28 |
| hsa-mir- 17 |
15 | 6 | 3 | 5 | 7 | 8 | 3 | 5 | 9 |
| hsa-mir- 145 |
18 | 2 | 0 | 1 | 2 | 3 | 1 | 2 | 5 |
Table 8: Comparison of predicted targets Second column shows the total number of experimentally validated interactions corresponding to each micro RNA. Column 3 to 9, out of the total valid interactions, the number of interactions predicted by seven popular target prediction tools. Column 10 shows predictions by HTar.
We have introduced an algorithm to find the binding sites of microRNA with less number of false positives and false negatives than existing algorithms. An HMM based seed predictor helps to provide better accuracy as well as faster completion of the overall operation by eliminating unnecessary computation in the case of non-targets. The developed model is based on structural, positional, thermodynamic properties of microRNA binding sites of 9 microRNAs with 148 mRNAs were compared with the results of experimentally validated binding sites and our results are more accurate than other tools.
Coding, data collection, writing of manuscript and figure generation are conducted by SA, design and data analysis is done by VSS.
This research is supported by College of Engineering Trivandrum, Kerala.