Radon ²²²Rn) is a naturally occurring radioactive gas generated by the decay of the naturally occurring ²³⁸U series [1,2]. Radon is directly produced by the decay of radium (²²⁶Ra) which is present in soil, rocks, building materials, underground and surface waters [1,3]. After generation it may dissolve in soil's pores and fluid. Thereafter, it migrates near or far through diffusion or convection and dilutes in atmosphere, surface and groundwater. Radon also dilutes into the atmosphere through release from its aqueous phase [1].

Radon and its progeny are the most significant natural sources of radiation exposure to the general population [3] contributing to about half of the total effective dose delivered to humans from all sources of ionizing radiation. The exposure is mainly delivered in domestic environments since the largest period of human lifetime is spent indoors. Therefore, the measurement and limitation of radon concentration of buildings are important [4].

Moreover, radon has been considered as an additional factor of radiation burden in stomach mainly due to water consumption [5,6]. Various organizations such as WHO, US-EPA and UNSCEAR [3,5,7] refer to this additional burden which can be estimated by measurements of radon concentrations in waters. Regarding Europe the maximum concentration values for radon are proposed by the European Commission [8]. Human exposure to high concentrations of radon and progeny has been correlated to lung cancer incidence [9,10]. For this reason, radon is considered to be a natural carcinogen of great importance.

The typical radon concentrations outdoors are low [3]. However, indoor radon may accumulate at significant levels. Radon accumulation depends on the radioactive properties of the underlying soil and rock, the building structure and the various ways of indoor ventilation and heating [1,3]. Radon in water contributes as well [11,12] and sometimes significantly [13].

During the last few years, several radon time-series were collected from Greek apartment dwellings. The aim of this work was to estimate Hurst exponents (H) of some of these radon time-series. One hundred twenty five radon signals were collected with Alpha Guard Pro and included, at least, one day active measurements in ten minutes cycles. Hurst exponents were calculated by the Rescaled Range (R/S) method. The scope was to identify whether indoor radon is governed by long-memory dynamics namely if persistent, anti-persistent traces can be identified or if the behavior is random, viz. the signals were uncorrelated. R/S method was applied through sliding on overlapping windows and lumping on non-overlapping sequential windows.

Hurst exponent

Hurst exponent (H) is a mathematical quantity which can detect long-range dependencies in time-series [14,15]. It can estimate the temporal smoothness of time-series and can search if the related phenomenon is a temporal fractal [16]. Hurst exponent was conceptualized for hydrology [14,15]. It has been employed however in other research topics as well, for example, traffic traces [17], plasma turbulence [18], ULF geomagnetic fields [19,20], climatic dynamics [21], pre-epileptic seizures [16], astronomy and astrophysics [22] and economy [23]. H-values between 0.5 < H < 1 manifest long-term positive autocorrelation in time-series. This means that a high present value will be, possibly, followed by a high future value and this tendency will last for long future time-periods (persistency) [24-27]. H - values between 0 < H < 0.5 indicate time- series with long-term switching between high and low values. Namely, a high present value will be, possibly, followed by a low future value, whereas the next future value will be high and this switching will last long into the future (antipersistency) [24-27]. H = 0.5 implies completely uncorrelated time-series.

Rescaled Range Analysis (R/S)

Hurst exponents were estimated through the method of Rescaled Range (R/S) [16] or as frequently referred, R/S analysis. The R/S analysis was introduced by Hurst [14] and attempts to find patterns that might repeat in the future. The method employs two variables, the range, R and the standard deviation, S, of the data. According to the R/S method, a natural record in time, X(N) = x(1), x(2),.., x(N), is transformed into a new variable y(n,N) in a certain time period N(N=1,2,…,N) from the average, 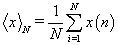over a period of N time units [14]. y(n,N) is called accumulated departure of the natural record in time [14]. The transformation follows the formula:

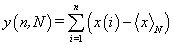         (1)

The rescaled range is calculated from (2) [14,16,28] :

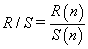         (2)

The range R(n) in (2) is defined as the distance between the minimum and maximum value of y(n,N) by :

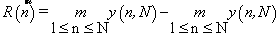         (3)

The standard deviation S(n) in (2) is calculated by :

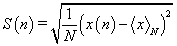         (4)

R/S is expected to show a power-law dependence on the bin size n

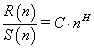         (5)

where H is the Hurst exponent and C is a proportionality constant.

The log transformation of the last equation is a linear relation 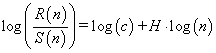(6),

         (6)

from which exponent H can be estimated as the slope of the best line fit.

Figure 1 represents a noteworthy case of indoor radon timeseries which evolved within approximately two days (47 hours). The corresponding dwelling (D1) was a basement apartment in Athens region. Radon accumulated continuously up to 8kBqm-3 and then decreased down to approximately 3kBqm^-3. The recorded concentrations were extremely high and considerably above the upper limit of 400 Bqm^-3 recommended by EU [8]. Three different conditions were applied for the R/S analysis of this dwelling; namely sliding window analysis of length 8 (Figure1a) and 32 (Figure1b) and lumping analysis of length 32 (Figure1c). It can be observed that large sliding windows (Figure1b) produced finer-less deviating Hurst exponents which were well concentrated around high H- bands. It is very important that all H - values of Figure1b were well above 0.9. It may be recalled that H - values between 0.5 < H < 1 manifest longterm positive autocorrelation in time-series. This means that high present values will be followed, on the most part, by high future values (persistency) while this tendency will last for numerous future timeperiods [24-28]. Therefore, the analysis of Figure1b indicates strongpersistent behaviour. Nevertheless, both the analysis of Figure1a (sliding windows) and the one of Figure1c indicate also the persistency of the signal'. Indeed, most of the H- values were above 0.7, viz., they were persistent. It is also very significant that almost all values of the Spearman’s correlation coefficients were successive (r2 > 0.95), namely they corresponded to a very linear log-log R/S fit.

Figure 1: Representative photomicrograph of histopathological features in pulmonary necropsies.

Figure 2 presents a typical case of radon concentrations often observed in Greek apartment dwellings [29,30]. Measurements in this dwelling (D2) spanned approximately four days. Recorded radon concentrations ranged between 10 Bqm^-3 and 100 Bqm^-3. As in Figure 1, most segments exhibited Hurst exponents between 0.5 and 1 with successive square Spearman’s correlation coefficient values above 0.98. This fact indicates that these radon time-series are persistent as well. The H - profiles however, deviate more compared to those of Figure 1. Despite this, only few H - values are below 0.5. The majority of segments are associated with Hurst exponents above 0.7. It is noticeable that in both Figures, the H - profiles do not follow those of radon concentration. Most importantly, this is observable in all sub- Figures, namely the tendency is independent of the selection of the window size. These observations provide strong indications regarding strong long-memory underlying dynamics which govern and drive the radon generating system. It is also interesting that larger size of sliding windows, produce also less deviating H - values, as in Figure1b. It should be noted however that the analysis should not exceed certain window sizes. For example, the 32 bin window size corresponds to 320 min (32x10min) analysis time. This is the power two window size closest to five hours. Larger windows would render analysis of larger time-windows and this will tend to smooth the H - values near large-deviating signal areas, such as peaks and downturns. It should be noted as well, that lumping generates H - histograms rather than H - profiles. For certain types of long-memory analysis, lumping is considered favorable [28,29,31] mainly because lumping renders to non-overlapping signal's areas. This fact is advantageous for lowdeviating segments of the time-series.

Figure 2: Representative photomicrograph of histopathological features in pulmonary necropsies.

Two more interesting results (dwellings D3 and D4) are shown in Figure 3. All Figures correspond to sliding window R/S analysis of window size 32 and window step 1. Hurst exponent profiles of both sub-Figures show analogous patterns which are similar to those of Figures 1b and 2b under identical conditions (window size 32, window step 1). These Figures provide further evidence of the underlying long-memory radon dynamics. Once again, the profiles of Hurst exponents are different from those of the variation of radon concentration. This is of extreme importance, especially if it is considered that radon concentration variations are affected by various factors and, most importantly, in a multivariate manner [32]. Radon concentrations of Figure 3 are below the EU upper action limit for radon concentration, viz. below 400 Bq.m-3. Both radon profiles are also typical for Greek apartment dwellings [30]. Figure 4 presents collectively the results from the R/S analysis of all investigated dwellings. Hurst exponents were calculated through sliding window analysis of window size 8 (Figure 4a), 16 (Figure 4b) and 32 (Figure 4c). As aforementioned, larger size of sliding windows produces less-deviating Hurst exponents. It is important that for all window sizes, the main percentage of each box-whisker plot is within the region of persistency, i.e. H - values above 0.5. From another perspective, this implies that the majority of Hurst exponents indicate persistency, either with window size 8, 16 or 32. It is more important, that a vast number of segments exhibited H - values above 0.7 or even 0.8. These segments indicate strong persistency of the corresponding parts of the radon concentration signal. Note, however, that when small window sizes are employed in R/S analysis (size 8 or 16), some antipersistent areas of the signals are identified. As already implied, a window size of 8 corresponds only to 80 minutes of time-series of indoor radon concentrations. This time duration is small enough to be biased by the several radon affecting factors. In this sense, the corresponding results just outline the signals' tendency in presenting persistent long-memory. They cannot evoke, in this consensus, emergence of any existing long-memory dynamics. These dynamics are emerged by the larger window size of 32. As also mentioned, this size is a good compromise between bias due to factors and smoothing due to radon peaking or downturn. It should be mentioned though that the 32-sample window-size rendered inconsistencies in some calculated Hurst exponents in twenty five radon time-series. For this reason, these series were excluded from the box-whisker plots of Figure 3c.

Figure 3: Representative photomicrograph of histopathological features in pulmonary necropsies.

Figure 4: Representative photomicrograph of histopathological features in pulmonary necropsies.

Several dwellings were accessed and their indoor radon concentrations were measured with active techniques. Time-series of at-least one day duration were employed in this study. Utilizing R/S analysis through sliding window and lumping, numerous Hurst exponents were calculated for each useful time-series. The majority of exponents were found to be in the range of 0.5 < H < 1 for the majority of the situations. This finding indicated persistency. Several exponents were above 0.8, namely the corresponding time-series parts were very persistent. In almost all cases it was found that indoor-radon dynamics are governed by chaos and long-memory.

The authors would like to thank I. Chaldeos, S.Filtisakos and A. Gardikioti for their assistance in preparatory analysis of some signals through R/S technique.