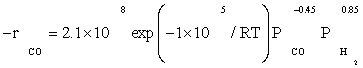Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
+44 1300 500008
ISSN: 2157-7544
+44 1300 500008
Research Article - (2012) Volume 3, Issue 2
The kinetic experiments of Fischer–Tropsch synthesis (FTS) over an industrial Co/K catalyst are carried out in a micro-fixed-bed reactor under the conditions as follows: temperature of 483–513K, pressure of 8bar, H2/CO feed ratio of 1–3, and space velocity of 132700–5200h-1. The optimal amount of catalyst containing 15wt.%Co/10wt.%K/Al2O3was prepared using impregnation procedure.The combined enol/carbide mechanism as the rate-p controlling step gives the most plausible kinetic model among the nine different models tested.The activation energies for optimal kinetic model and power law equation were obtained 111.5kJ/mol and 100 kJ/mol, respectively.
Keywords: Fischer-Tropsch Synthesis; Fixed-bed Reactor; Co/K/Al2O3 Catalyst; Kinetic Modeling
The process of converting the synthesis gas into liquid fuels (FTS) is a well-known technology. This method is a promising, developing option for environmentally sound production of chemicals and fuels from coal and natural gas. In view of large coal and natural gas reserves and dwindling petroleum reserves worldwide, it is projected to play an ever increasing role in the coming decades [1,2] .
Cobalt-based catalysts are the preferred catalysts for hydrocarbon synthesis because of their high FTS activity, selectivity for long-chain paraffins and low activity for the water–gas shift reaction [3]. Cobalt and Iron-based catalysts often contain small amounts of potassium and other metals such as manganese, calcium, zinc, copper and magnesium as promoters to improve their activity and selectivity [4]. Due to its stronger basicity, potassium has a stronger influences on adsorption of reactants (CO and H2) on the active sites, and leads to improvements in FTS activity, enhancement in selectivity to olefins, suppression of methane formation and a selectivity shift to higher molecular weight products [5,6].
The kinetics of FTS on cobalt catalysts has received significant attention; in fact, several previous studies [7-11] report kinetic data and rate expressions. Reaction orders for H2 and CO are in the range 0.5 to 2 and −1.0 to +0.65, respectively; activation energies from these studies cover a range 98-103 kJ/mol [11]. The mechanistic kinetic rate expressions for cobalt catalysts are based on the formation of the monomer species as the rate-determining step in the consumption of synthesis gas. Many kinetic equations have been proposed in the literature for various cobalt catalysts, and these have been obtained either empirically (using a power-law rate equation) or to fit a proposed mechanism [8-14].
Our objective was to develop intrinsic rate expressions for the CO conversion to Fischer–Tropsch products over an impregnation cobalt catalyst on the basis of realistic mechanisms. The kinetics of FT reaction was studied and the rate expressions were tested against experimental data that was obtained on the selected catalysts. A model was successfully devised and the kinetics parameters were determined. Also, a power law kinetic equation for the carbon monoxide rate was obtained.
Catalyst preparation
The optimal amount of 15wt.%Co/10wt.%K/Al2O3 was prepared by impregnation with an aqueous solutions of Co (NO3)2.6H2O and KNO3 to incipient wetness of γ-Al2O3, which had been previously calcined at 400ºC for 8 h to remove the surface adsorbed impurities (Brunauer– Emmett–Teller (BET) surface area of 217 m2/g, pore volume of 0.7 cm2/g). The impregnated sample was dried at 110ºC for 2 h and calcined in air at 400ºC for 8 h (heating rate of 10ºC between 110ºC and 400ºC); the calcined catalyst was reduced in situ (in the fixed bed reactor described below) in pure H2 at 400ºC for 16 h (heating rate of 10ºC between 25 and 400ºC).
Fixed bed reactor system
A schematic representation of the experimental setup is shown in Figure 1. FTS was carried out in a fixed-bed micro-reactor made of stainless steel with an inner diameter of 12 mm. Three mass flow controllers (Brooks, Model, 5850E) were used to adjust automatically flow rate of the inlet gases comprising CO, H2 and N2 (purity of 99.999%). Mixture of CO, H2 and N2 was subsequently introduced into the reactor, which was placed inside a tubular furnace (Atbin, Model ATU 150-15). Temperature of the reaction was controlled by a thermocouple inserted into the catalytic bed and visually monitored by a computer. The catalyst was in situ pre-reduced at atmospheric pressure under H2–N2 flow (N2/H2 = 1, flow rate of each gas = 30 ml/ min), at 400°C for 16 h. In each test, 1.0 g catalyst was loaded and the reactor operated about 12 h to ensure steady state operations were attained.
Figure 1: Schematic representation of the reactor used. (1) Gas cylinders, (2) pressure regulators, (3) needle valves, (4) mass flow controllers (MFC), (5) monometers, (6) non-returns valves, (7) ball valves, (8) tubular furnace, (9) reactor, (10) catalyst bed, (11) trap, (12) condenser, (13) silicagel column and (14) gas chromatograph (GC).
Catalytic evaluation
Experiments were conducted with mixtures of H2, CO and nitrogen in a temperature range from 210 to 240°C, H2/CO feed ratios of 1/1-3/1 (mol/mol) at the pressure of 8 bar. The arrangements of the parameters and the related levels are shown in Table 1. In all of the experiments, the space velocities were between 2700 and 5200 h-1.
| Number of data | Temperature (K) | XCO (%) | PH2(bar) | PCO (bar) | F/W (mol/gr cat. h) |  (mmol/gr cat. h) (mmol/gr cat. h) |
| 1 | 483.15 | 2.6 | 2.81 | 1.95 | 0.172 | 4.471 |
| 2 | 483.15 | 3.2 | 2.35 | 2.90 | 0.173 | 5.55 |
| 3 | 483.15 | 3.6 | 3.55 | 1.93 | 0.154 | 5.528 |
| 4 | 483.15 | 4.8 | 2.25 | 3.81 | 0.139 | 6.659 |
| 5 | 493.15 | 3.2 | 3.05 | 1.94 | 0.289 | 9.254 |
| 6 | 493.15 | 2.4 | 1.41 | 1.95 | 0.195 | 4.687 |
| 7 | 493.15 | 5.3 | 3.33 | 2.84 | 0.287 | 15.20 |
| 8 | 493.15 | 2.8 | 2.59 | 0.97 | 0.143 | 4.002 |
| 9 | 503.15 | 5.1 | 1.81 | 1.90 | 0.186 | 9.505 |
| 10 | 503.15 | 7.9 | 4.73 | 1.84 | 0.355 | 28.01 |
| 11 | 503.15 | 5.5 | 3.61 | 1.42 | 0.272 | 14.94 |
| 12 | 503.15 | 6.7 | 2.23 | 2.80 | 0.286 | 19.16 |
| 13 | 513.15 | 8.8 | 2.88 | 3.65 | 0.698 | 61.42 |
| 14 | 513.15 | 7.6 | 3.63 | 2.31 | 0.650 | 49.42 |
| 15 | 513.15 | 7.1 | 3.41 | 1.86 | 0.520 | 36.92 |
| 16 | 513.15 | 8.6 | 4.58 | 2.29 | 0.712 | 61.22 |
Table 1: Summary of experimental conditions and results at P = 8 bar and T = 210-240ºC.
To avoid the effect of deactivation, fresh catalysts were loaded in each experiment. To achieve the isothermal conditions in a catalytic bed, the catalyst was diluted with an inert material (quartz). Axial temperature distribution was ensured using Mear’s and Mollavali et al. [15,16] criterion, that is with L/dp > 50. Also, plug-flow was assumed for the gaseous feed. The experimental reaction rate was determined as follows:
 (1)
(1)
Kinetic expressions
In order to derive rate equations to be adjusted with the data in Table 1, we used Langmuir–Hinshelwood–Houngen–Watson (LHHW) theory to obtain kinetic models. According to this theory, a reaction mechanism should be adopted. Two key assumption of this theory is: (1) Attraction heats are constant, (2) Inherent reaction rates are proportional to surface covers of reactors. To simplify the kinetic models, following assumptions are taken into consideration [17,18]: (1) Presence of an irreversible controlling stage, although all of the other stages are considered to be near the thermodynamic equilibrium. (2) Concentrations of all of the mediums on the catalyst surface are in steady state. (3) Catalytic locations are steady and distributed homogenously. (4) Throughout the temperature and pressure region, rate controller stage and the most abundant surface medium are remained unchanged. (5) Elementary attraction of hydrogen and carbon monoxide in pseudo-equilibrium state are within concentrations of gaseous phase. (6) Water is removed after the CO decomposition irreversibly.
Statistical criteria using polymath software
Least square method and non-linear regression analysis based on the summarized values in Table 1 was used to determine the power-law equation parameters and kinetic model parameters from experimental data provided in Table 2 using Polymath® software. The software uses Levenberg–Marquardt algorithm to estimate the constants of the model. There are some conditions to find the best model [19]: (1) Obtained constants must be positive. (2) Optimal model or equation is the one which gives the reliable R2. (3) Coefficients of the equation must obey Arrhenius and Vanthouff rules. (4) The equation must have the ability to predict the behavior of a differential reactor. A good equation can satisfy all of the mentioned rules. Different statistical indices in Polymath software can be used to determine the quality of regression models and compare them.
Development of kinetic equations
Considering the proceeding assumptions, three mechanisms were offered on the basis of various monomer formation (elementary reactions) and carbon chain distribution pathways. An elementary reactions set on sites for each model is summarized in Table 2.
| Model | Number | Elementary Reaction |
| FT-I | 1 2 3 4 5 6 7 8 |
CO + s ↔ COs COs + s ↔ Cs + Os H2 + 2s ↔ 2Hs Cs + Hs ↔ CHs + s CHs + Hs ↔ CH2s + s Os + Hs → HOs + s HOs + Hs → H2Os + s H2O + s → H2Os |
| FT-II | 1 2 3 4 5 6 7 |
CO + s ↔ Cos H2 + 2s ↔ 2Hs COs + Hs ↔ HCOs + s HCOs + Hs ↔ Cs +H2Os Cs + Hs ↔ CHs + s CHs + Hs ↔ CH2s + s H2O + s → H2Os |
| FT-III | 1 2 3 4 5 6 7 8 |
CO + s ↔ COs COs + H2 ↔ H2COs H2COs+ H2 ↔ CH2s + H2O COs + s ↔ Cs + Os Cs + Hs ↔ CHs + s CHs + Hs ↔ CH2s + s Os + H2 → H2Os H2O + s → H2Os |
Table 2: Elementary reactions mechanism set for FTS.
To derive each kinetic model, initially one of the elementary reaction (in some case two or three) steps was assumed as rate-determining step and all other steps were considered at equilibrium. Then, all of the models obtained were fitted separately against the experimental data. In the interest of conciseness, only certain selected kinetic models are reported in the Table 3.
| Model of rate controlling | Kinetic equation |
|---|---|
| FT-I1 | 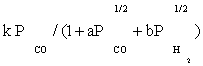 |
| FT-I3 | 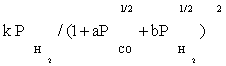 |
| FT-I4 | 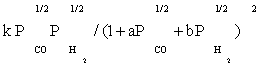 |
| FT-I5 | 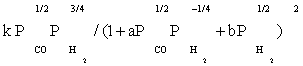 |
| FT-II1 | 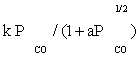 |
| FT-II3 | 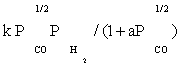 |
| FT-III1 | 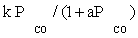 |
| FT-III2 | 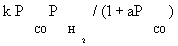 |
| FT-III3 | 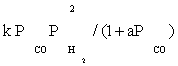 |
Table 3: Reaction rate expressions for the FTS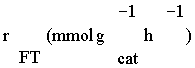 .
.
For example derivation of the rate equation for FT-I4 is explained here. To do this, the first step was considered to be the rate limiting stage and the reaction was irreversible. The remaining steps can be considered to be quick and at equilibrium.
The rate expression of the rate-determining step for FT-I4 model where surface carbon reacts with adsorbed dissociated hydrogen as the rate limiting step, can be expressed irreversible adsorption as follows:
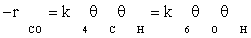 (2)
(2)
where −rCO is the rate of disappearance of CO, k4 and k6 are the forward rate constant for elementary reaction of numbers of 4 and 6 respectively, and θi is the surface fraction occupied with adsorbed species i. The fraction of vacant sites, θS, can be calculated from the following balance equation:
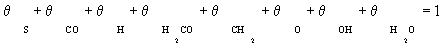 (3)
(3)
In this case, it is assumed that adsorbed dissociated hydrogen and surface carbon occupies a significant fraction of the total numbers of sites. Other species were assumed to be negligible in the stoichiometric balance:
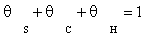 (4)
(4)
The surface coverage of carbon monoxide and adsorbed dissociated hydrogen are calculated from the site balance, and the preceding reaction steps which are at quasi-equilibrium:
 (5)
(5)
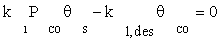 (6)
(6)
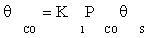 (7)
(7)
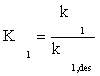
where K1 is the equilibrium constant of CO adsorption step. Thus, if the next stages are assumed to be near the thermodynamic equilibrium, available surface ratios can be determined using partial pressures of reactors.
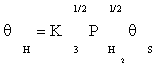 (8)
(8)
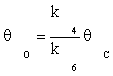 (9)
(9)
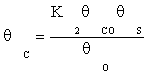 (10)
(10)
Substituting equation (7) and then (9) in equation (10) gives:
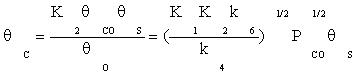 (11)
(11)
Substituting Equation (8) and (11) into Equation (4), the ratio of free active site can be expressed as:
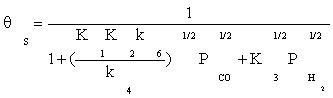 (12)
(12)
Substitution of the fraction of vacant sites in Equation (2), the final rate expression is obtained as:
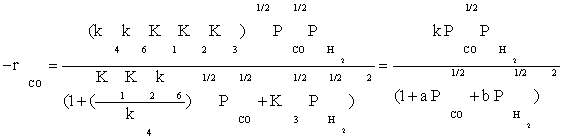 (13)
(13)
Table 3 summarizes the final form of the different rate expressions for the 9 possible kinetic models considered, whereas Table 4 shows the kinetic and adsorption parameters for the several kinetic models. It can be seen that the pressure dependency of CO and H2 in the numerator ranges from 1/2 to 1, and 1/2 to 2, respectively. The denominator is quadratic in case of a dual site elementary reaction, in contrast to a single site rate-determining step. The denominator consists of the individual contributions of significantly plentiful species on the catalyst surface.
| Model of rate controlling | k (x) (mmol g-1 h-1 barx) | a(x) (barx) | b (x) (barx) |
|---|---|---|---|
| FT-I1 | k1 (-1) | (k6K1K2 / k4)1/2 (-1/2) | k31/4(-1/2) |
| FT-I3 | k3 (-1) | (k6K1K2 / k4)1/2 (-1/2) | k31/4(-1/2) |
| FT-I4 | (k4k6K1K2K3)1/2(-1) | (k4K1K2 / k6)1/2 (-1) | k31/4(-1/2) |
| FT-I5 | (k3k6K1K2K4)1/2k31/4(-5/4) | (k6K1K2 / k5K4)1/2k3-1/4(-1/4) | k31/4(-1/2) |
| FT-II1 | k1 (-1) | (K1K2K4 / k3)1/2 (-1/2) | |
| FT-II3 | (k3k4K1K2)1/2(-3/2) | (K1K2K4 / k3)1/2 (-1/2) | |
| FT-III1 | k1 (-1) | K1 (-1) | |
| FT-III2 | k2K1 (-2) | K1 (-1) | |
| FT-III3 | k2K1K2(-3) | K1 (-1) |
Table 4: Parameters for the FT kinetic models.
| Equation | k0 (mol.g Cat-1 .h-1.barx) | E(kJ/mol) | a0(bar-0.5) | ΔH(kJ/mol) | m(-) | n(-) |
| a FT-III2 | 1.01x1011 | 111.5 | 163.2 | - 5.26 | ||
| b Power law | 2.1x108 | 100 | -0.45 | 0.85 |
x: a = - 2, b = - 0.4
Table 5: Values of the kinetic parameters, activation energy and heat of adsorption of CO with various equations.
Also, power law kinetic equation for the carbon monoxide rate was considered for comparison with experimental data. Yang et al.[8] obtained empirical rate expressions for supported cobalt catalysts using a fixed-bed reactor via regression of a power-law equation of the general form:
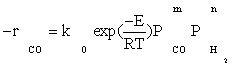 (14)
(14)
Where PCO is the partial pressure of carbon monoxide, k0 the reaction rate constant, E the activation energy of CO consumption, m the reaction order for CO, and n the reaction order for H2.
Model parameters and model discrimination
CO consumption rate was obtained from the data in Table 1 using the differential method of data analysis. The kinetic data presented in Table 1 for CO conversion were used for testing the power law equation and nine models listed in Table 3. Before inserting the equations in the Polymath® software, Arrhenius and adsorption equations were substituted in kinetics models: Equation (15) and Equation (16) were substituted for k and a, respectively.
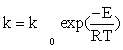 (15)
(15)
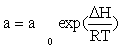 (16)
(16)
According to the statistical results obtained by inserting the data and models, the best model can be selected. Based on the kinetic data, the only plausible mechanism was found to be the FT-III model with combined enol/carbide mechanism as the rate-controlling step.
Atashi and Gharehbaghi [20] reported that carbide mechanism was the CO hydrogenation mechanism over Co/TiO2 catalyst, and indicates that potassium addition causes intermediate to be oxygenated. However, based on statistical information, the best model was found to be FT-III2 that had the less deviation from experimental data. Therefore, the data were best fitted by a LHHW approach by the rate form
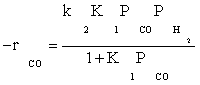 (17)
(17)
where activation energy was obtained to be 111.5 kJ/mol.
The other models were ignored because: (1) calculations of partial regression related to kinetic equation exceed the maximum number of iterations or trial and errors, (2) confidence interval parameter was high when compared with its absolute values, (3) their constants were negative, (4) did not give the responsible R2. Figure 2 shows a comparison between the experimental data and predicted results of the FT-III2 model. The solid line in the figure denotes that calculated is equal to the experimental one and dotted lines over and under the solid line represent 11% deviation. The experimental results were found to have a good agreement with the optimal kinetic model showing about 11% deviation.
The data of this study were fitted fairly well by a power law equation in the form of 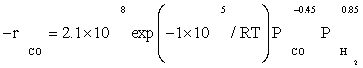 . The R2 value was obtained to be 0.99, which shows power law equation was well matched with the experimental data. Table 5 shows the kinetic parameters calculated for the kinetic FT-III2 model and power law equation. The apparent activation energies were 111.5 and 100 kJ/ mol which were very close to activation energies reported previously: 100 and 103 kJ/mol reported by Yang et al. [8] and Storch et al. [21], respectively. Nevertheless, it was substantially lower than the value of 142 kJ/mol reported by Reuel and Bartholomew [22]. However, Reuel and Bartholomew’s value was obtained at significantly lower reactant partial pressure and was based on only two data points, while in this study it was based on sixteen data points.
. The R2 value was obtained to be 0.99, which shows power law equation was well matched with the experimental data. Table 5 shows the kinetic parameters calculated for the kinetic FT-III2 model and power law equation. The apparent activation energies were 111.5 and 100 kJ/ mol which were very close to activation energies reported previously: 100 and 103 kJ/mol reported by Yang et al. [8] and Storch et al. [21], respectively. Nevertheless, it was substantially lower than the value of 142 kJ/mol reported by Reuel and Bartholomew [22]. However, Reuel and Bartholomew’s value was obtained at significantly lower reactant partial pressure and was based on only two data points, while in this study it was based on sixteen data points.
The reaction orders of 0.85 and –0.45 for H2 and Co obtained in this study (power law equation) were consistent with those reported in previous kinetic studies of FTS on supported cobalt [8,12,13]. Reaction orders from these studies for H2 and Co were in the range 0.68 to 1 and –0.24 to –0.5, respectively.
The optimal amount of catalyst containing 15wt.%Co/10wt.%K/ Al2O3 was prepared using impregnation procedure. Experiments for the kinetics of the hydrocarbon formation over a cobalt catalyst were obtained over a wide range of industrially relevant reaction conditions. The data of this study were best fitted by the simple LHHW approach by the rate form 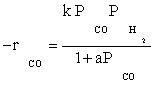 . The values of kinetic constants were obtained and the activation energy was found to be 111.5 kJ/mol for the best model. The data were fitted fairly well by a power law equation in the form of
. The values of kinetic constants were obtained and the activation energy was found to be 111.5 kJ/mol for the best model. The data were fitted fairly well by a power law equation in the form of