Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2015) Volume 4, Issue 3
This paper considers the theoretical problem of hydrodynamic and slips boundary conditions over an exponential stretching sheet in the presence of radiation and heat generation/absorption. Similarity solutions are obtained from the governing boundary layer equations for different various of slip parameters, exponential parameter, magnetic field parameter, radiation parameter, heat source parameter, thermophoretic parameter and porosity parameter. The resulting couple system of equations which is highly nonlinear ordinary differential equations are solved semianalytically using homotopy analysis method (HAM). Numerical results are obtained for non-dimensional governing parameters on skin friction, heat and mass transfer coefficient in the presence of suction. Comparison with published results seen in literature is in perfect agreement.
<Keywords: HAM; Radiation; Hydromagnetic; Exponential parameter; Slip boundary condition; Porosity
The boundary layer flows play a vital role in different areas of fluid mechanics as results of motion of a viscous fluid close to the surface. This stems from different fields of engineering and metallurgical applications such as wire drawing, hot rolling, plastic and metal extrusion, glass fiber production, paper production and crystal growing.
Flow and heat transfer features past a stretching sheet have important role in industrial applications, for example, extrusion of polymer sheet from a die. In the process of manufacturing sheets, the melt process from a slit and is thereafter stretched. The rates of cooling and stretching have a great influence on the quality of the finished product with desired features. This processes which involved cooling of a molten liquid through drawing into a cooling system. At first is the cooling liquid used then thereafter is the rate of stretching are the processes involved. Weak electrical conductivity of non-Newtonian fluid can be chosen for cooling fluid as their flow and after mentioned the regulated the heat transfer rate through some external medium. Highest rate of stretching is vital as results in sudden solidification then destroying the properties expected from the final product.
After the pioneering study of Hayat et al., [1] a great number of research works on a stretching sheet have been investigated and published by considering different governing parameters. The problem of radiative magnetohydrodynamic flow of Jeffrey nanofluid by an exponentially stretching sheet was resolved by Hussain et al., [2]. Hayat et al., [3] considered flow of viscoelastic fluid using thermal radiation and convective boundary condition on threedimensional mixed convection fluid flow. Madhu et al., [4] presented an investigation on hydromagnetic mixed convection stagnation point flow of a power-law by using Non-Newtonian nanofluid close to a stretching surrounding with radiation and heat source/ sink. Hayat et al., [5] worked on influence of inclined magnetic field in flow of third grade fluid flow in the presence of variable thermal conductivity. Effects of Newtonian heating on hydrodynamic flow of couple stress Nanofluid in the presence of viscous dissipation and Joule heating was discussed by Ramzan [6]. Hayat et al., [7] investigated temperature and concentration stratification influence on mixed convection flow of an Oldroyd-B fluid in the presence of thermal radiation and chemical reaction. Nield et al., [8] worked on external natural convection through the porous media. Magnetohydrodynamic mixed convection on stagnation point fluid flow of a power law Non- Newtonian Nanofluid closed to a stretching surrounding medium in the presence of radiation and heat source was presented by Madhu and Naikoti [9]. Narayana et al., [10] used Numerical techniques to resolve the problem of magnetohydrodynamic heat and mass transfer of a Jeffrey fluid flow past a stretching sheet in the presence of chemical reaction and thermal radiation. Hayat et al., [11] investigated on the problem of three-dimensional flow past an exponentially stretching sheet medium in porous medium, chemical reaction and heat source/ sink. Convection heat and mass transfer in hydromagnetic mixed convection flow of Jeffrey nanofluid past a radially stretching surface in the presence of thermal radiation was presented by Ashraf et al., [12]. Lakshmi and Suryanarayana [13] studied radiation on mixed convection flow of a Non-Newtonian nanofluid past a Non-linearly stretching sheet in the presence of heat source/sink. Hayat et al., [14] investigated Joule heating and thermal radiation in flow of third grade fluid over a radiative surface. Similarity solution to three dimensional boundary layer flow of second grade nanofluid flow over a stretching surface in the presence of thermal radiation and heat source/sink was presented by Hayat et al., [15].
Khan et al., [16] discussed on three dimensional of Oldroyd-B nanofluid flow closed to stretching surface in the presence of heat generation/absorption. An extension was made by Mabood et al., [17] to hydromagnetic flow past a non-isothermal stretching sheet with heat generation/absorption and transpiration using approximate analytical modeling. Effects of convective heat and mass transfer in hydromagnetic fluid flow of a nanofluid were discussed by Shehzad et al., [18]. Time dependent hydromagnetic Nano-Second Grade fluid flow was investigated by Ramzan and Muhammad [19] using induced by permeable vertical stretching sheet. Lin et al., [20] investigated hydromagnetic pseudo-plastic nanofluid using finite thin film on unsteady flow and heat transfer over stretching sheet with internal heat generation. An extension was made by Hayat et al., [21] to Jeffrey fluid flow over a bidirectional stretching sheet in the presence of source/sink.
Swapna et al., [22] used finite element analysis on radiative mixed convection magneto-micropolar fluid flow in a Darcian porous material in presence of variable viscosity and convective surface condition. Influence of thermophoresis and heat generation/absorption of hydromagnetic flow in the presence of oscillatory stretching sheet and chemically reactive species was presented by Sheikh and Zaheer [23]. Hayat et al., [24] presented a work on boundary layer flow of Maxwell nanofluid using semi-analytically method of solution (HAM).
Slip flow and hydromagnetic of nanofluid past an exponentially stretching sheet with permeable material in the presence of heat generation/absorption was discussed by Ranga Rao et al., [25]. Shen et al., [26] work on hydromagnetic mixed convection slip flow closed to a stagnation point flow with nonlinearly vertical stretching materials. Rashidi et al., [27] investigated on Double Diffusive hydromagnetic mixed convection slip flow.
The aim of the paper is to study theoretically the slip boundary conditions in velocity, temperature and concentration on the boundary layer flow and heat transfer of a nanofluid. Aftermentioned considered the no-slip thermal and solutal boundary condition. Effects of slip conditions are vital for fluids that shows wall slip seen in polymer solutions, suspensions, emulsions, foams, etc. Nanofluid exhibiting slips are vital in different technological areas of application such as in the polishing of internal cavities and artificial heart values. But in some instance where no-slip boundary condition may not be applicable, we may be force to look into slip boundary condition. In this case, this study fulfills this gap. The study investigated magnetohydrodynamic nanofluid flow in the presence of radiation and heat generation/ absorption over an exponential stretching sheet with velocity, thermal, and solutal slip boundary condition. Moreso, the combined influences of exponential parameter, magnetic field parameter, radiation parameter, heat source parameter, thermophoresis parameter, and porosity parameter on heat transfer and boundary layer flow due to nanofluid are studied.
Consider two-dimensional steady, electrically conducting, incompressible viscous flow of a nanofluid with dissipative past an exponentially stretching sheet in permeable medium. Chosen a fluid stagnation-point flow been the origin of the coordinate system such that the x-axis is flat (direction) and y=0. The fluid flow surrounding is confined to y-axis is normal to the surface. In the x-axis we have two equal and opposite force on the stretching flat sheet such that the wall is continuous stretching along the initial fixed direction. The permeable medium with non-uniform permeability k is taken with a variable magnetic field B(x) is chosen along y direction. A variable heat source/sink Q (x), influence of suction/injection and thermophoretic are incorporated. The continuous stretching surface of the temperature and the nanoparticle fraction are said to have constant value Tw and Cw respectively. For large value of y, the temperature and nanoparticle fraction are deemed to have constant values T∞ and C respectively. The boundary layer governing equations of the fluid flow and temperature subjected to Boussinesq approximations are given as follows:
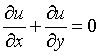 (1)
(1)
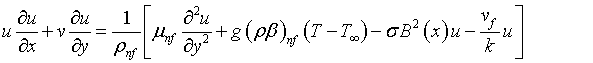 (2)
(2)
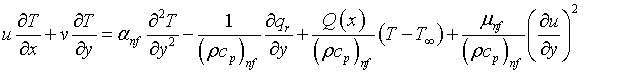 (3)
(3)
 (4)
(4)
The boundary conditions for the problem are given as follows:
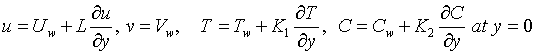
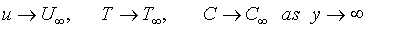 (5)
(5)
where 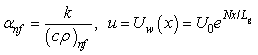 is the surface velocity and
is the surface velocity and 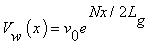 is the velocity at the surface. The velocity components along x and y-axis are u and v respectively. v is the kinematic viscosity, T is the temperature inside the boundary layer,
is the velocity at the surface. The velocity components along x and y-axis are u and v respectively. v is the kinematic viscosity, T is the temperature inside the boundary layer,  effective heat capacity of the nanoparticle, ρ is the density,
effective heat capacity of the nanoparticle, ρ is the density, 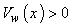 is the suction and
is the suction and 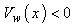 represents injection on the permeable surface. The radiative heat flux qr under Rosseland approximation is given by
represents injection on the permeable surface. The radiative heat flux qr under Rosseland approximation is given by
 (6)
(6)
Here σ1 and k are the Stefan-Boltzmann constant and mean absorption coefficient, respectively. Let the temperature difference in the flow be sufficiently small in such a way that the term T4 will be expressed as linear function of temperature. By using Taylor series about a free stream temperature T∞ is represented as
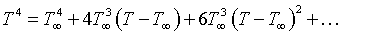 (7)
(7)
By neglecting higher-order terms in equation (7) beyond the first order in (T-T∞) we have:
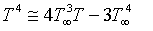 (8)
(8)
Substituting equation (8) in equation (6) we get:
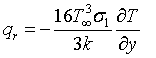 (9)
(9)
We now defined similarity transformation variables as follows:
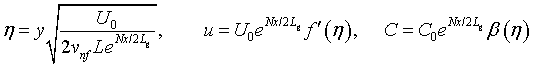
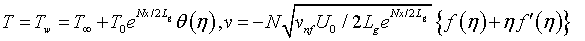 (10)
(10)
The equation of continuity is satisfied if a stream function Ψ ( x, y) is defined as:
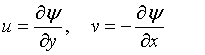 (11)
(11)
Using the similarity transformation variables, the governing partial differential equations (1)-(4) are now transformed to ordinary differential equation as presented:
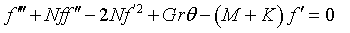 (12)
(12)
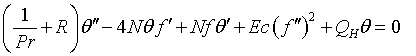 (13)
(13)
 (14)
(14)
With boundary conditions:
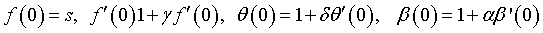
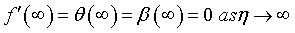 (15)
(15)
Where the governing parameters are given as follows:
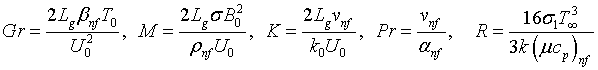
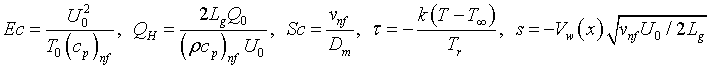
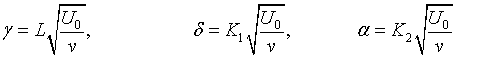 (16)
(16)
Where Gr is the thermal Grashof number, M is the Hartmann number, K is the porosity parameter, Pr is the Prandtl number, R is the radiation parameter, Ec is the Eckert number, QH is the internal heat source/sink, Sc is the Schmidt number, is the thermophoretic parameter, s is the permeability of the porous surface (s>0 is suction and s<0 is injection). γ,δ,α are velocity, thermal and concentration slip parameters, respectively. f ′,θ & β are the dimensionless velocity, temperature and nanoparticle concentration respectively and Prime represents differentiation with respect to η (similarity variable). The physical quantities of interest in our problem are the local skin friction coefficient cf, the local Nusselt number Nux and the local Sherwood number shx, Reynolds number Rex are defined as:
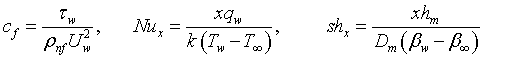 (17)
(17)
Where the mass heat flux hm and wall heat flux qw are presented as:
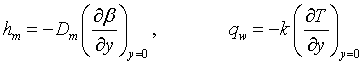 (18)
(18)
From the above equations, we have:
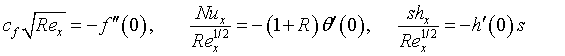 (19)
(19)
In this section, we will apply HAM an idea from Liao [28-34] to solve equations (12)-(15). We choose the set of base functions { 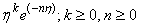 is an integer} to approximate the unknown functions f (η), θ (η) and β(η) respectively, as
is an integer} to approximate the unknown functions f (η), θ (η) and β(η) respectively, as
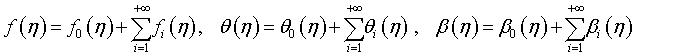 (20)
(20)
where
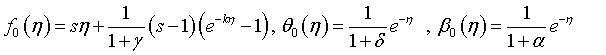 (21)
(21)
The auxiliary linear operators are selected as:
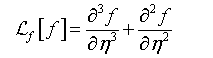 (22)
(22)
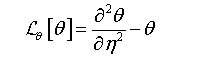 (23)
(23)
 (24)
(24)
are taken to be the initial guess approximations, with the property:
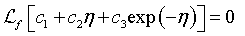 (25)
(25)
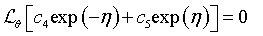 (26)
(26)
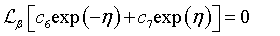 (27)
(27)
Here ci (where i=1,2,3,4,5,6,7) are they constants. Base on equations (17) and (18), the non-linear operators
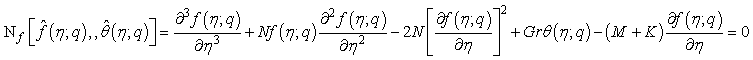 (28)
(28)
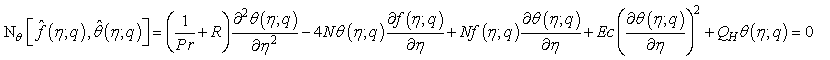 (29)
(29)
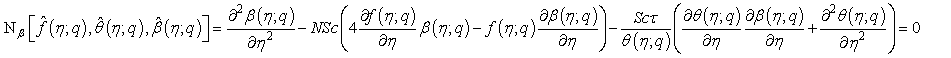 (30)
(30)
Where 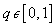 is an embedding parameter, and
is an embedding parameter, and 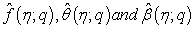 are kind of mapping function for f(η), θ (η), and β (η) respectively. From the operators, we can construct the zeroth-order deformation equations as:
are kind of mapping function for f(η), θ (η), and β (η) respectively. From the operators, we can construct the zeroth-order deformation equations as:
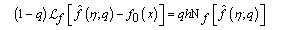 (31)
(31)
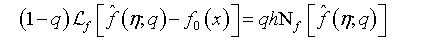 (32)
(32)
 (33)
(33)
Where h is an auxiliary non-zero parameter. The boundary conditions for equations (31)-(33) are presented as:

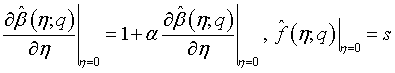 (34)
(34)
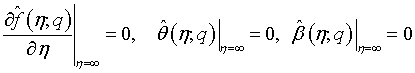 (35)
(35)
Clearly, when q=0 and q=1, the above zeroth-order deformation equations have the following solutions.
 (36)
(36)
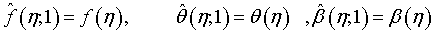 (37)
(37)
When q increases from 0 to 1, and 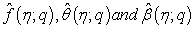 vary from
vary from 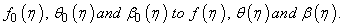 From Taylor’s theorem and expanding equation (36), we obtained
From Taylor’s theorem and expanding equation (36), we obtained
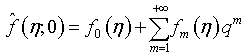 (38)
(38)
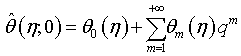 (39)
(39)
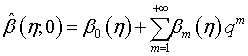 (40)
(40)
where
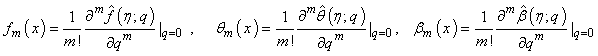 (41)
(41)
The convergence of the series solutions (38)-(40) depend upon the choice of auxiliary parameter h. Assume that h is chosen such that the series solution (31)-(33) are convergent at q=0 & q=1, then due to equations (38)-(40). The i th-order deformation equations, we differentiate equations (31)-(33) up to m times with respect to q and divide by m! and then set q=0. The resulting deformation equation at the m th-order are
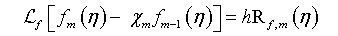 (42)
(42)
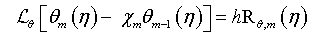 (43)
(43)
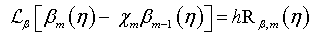 (44)
(44)
with the following boundary conditions
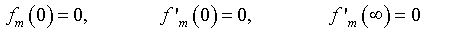 (45)
(45)
 (46)
(46)
 (47)
(47)
where
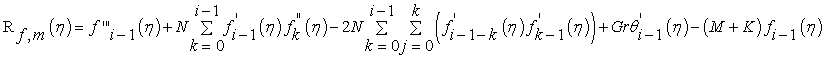 (48)
(48)
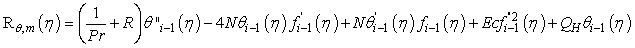 (49)
(49)
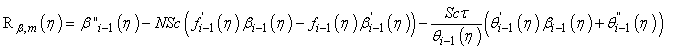 (50)
(50)
and
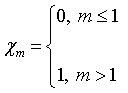 (51)
(51)
The general solutions of equations (39)-(44) which can be represent as follows:
 (52)
(52)
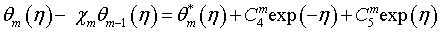 (53)
(53)
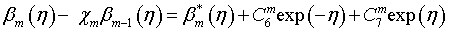 (54)
(54)
Assume 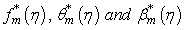 represent the particular solutions of equations (31)-(33), one after the other as
represent the particular solutions of equations (31)-(33), one after the other as 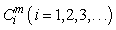 the computation, can easily be compute by symbolic computation software such as Mathematica, Maple, Matlab etc for m=1,2,3… in that order. Now by computation using homotopy analysis method (HAM) the problems containing equations (42)-(44) see Hayat et al., [31]. Therefore, the Figures 1 and 2 are shown to determine the values of auxiliary parameters hf, h and hβ for the convergent solutions. It was found that the admissible convergent ranges are
the computation, can easily be compute by symbolic computation software such as Mathematica, Maple, Matlab etc for m=1,2,3… in that order. Now by computation using homotopy analysis method (HAM) the problems containing equations (42)-(44) see Hayat et al., [31]. Therefore, the Figures 1 and 2 are shown to determine the values of auxiliary parameters hf, h and hβ for the convergent solutions. It was found that the admissible convergent ranges are 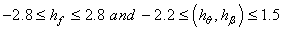 respectively. It obvious the solutions converges in the whole region of η (0< η<∞) for hf, hθ andhβ= - 0.5
respectively. It obvious the solutions converges in the whole region of η (0< η<∞) for hf, hθ andhβ= - 0.5
The graphical and numerical results representative of velocity, temperature, concentration, skin friction, heat and mass transfer coefficients, for various values of the thermophysical parameters controlling the dynamics nanofluid in the flow region. In Table 1 below shows the numerical values in order to validate the new computation scheme of our studied using homotopy analysis method (HAM). The results for special case of the current study (i.e permeable flat surface s=0.5 are compared with the work of Sandeep and Sulochana [35]. It was found that the theoretical results are in perfect agreement with the one published in literature. This gives us the confidence on our new approach scheme to the numerical results seen and reported subsequently. Figure 3 shows the effects of exponential parameter on the velocity profile when (s<0) injection. For different values, the nanofluid velocity decreases from the fixed plate surface and hence attains the free stream value which statisfied the boundary conditions. Generally, the momentum boundary layer thickness decreases with increases in the fluid exponential parameter at the plate surface. For suction see Figure 4. Similar trend happened, but is more pronounced in injection(s<0). Figure 5 illustrates the influence of exponential parameter on temperature profile. The nanofluid temperature gets to the highest at the plate surface and decreases greatly to zero free stream value satisfying the boundary conditions. An increase in fluid exponential parameter yields a decrease in the plate surface temperature and the thermal boundary layer thickness. Notice that the thermal boundary layer thickens with exponential parameter leading to an increasing in nanofluid temperature. Figure 6, shows the effects of exponential parameter on the concentration profile. It is observed that an increase in the exponential parameter decreases the concentration profile. The exponential parameter decreases the concentration boundary layer thickness.
| Pr | N | M | K | R | QH | τ | Gr | Sc | Sandeep, Sulochana [35] | Present Result | |||||||
| f’’(0) | θ’(0) | Β’(0) | f’’(0) | θ’(0) | Β’(0) | ||||||||||||
| 1 | -2.0552323 | 2.390596 | 2.560407 | -2.552322 | 2.390597 | 2.560407 | |||||||||||
| 1 | -2.551039 | 2.307011 | 2.554629 | -2.551039 | 2.307011 | 2.554628 | |||||||||||
| 1 | -2.626792 | 2.304187 | 2.552583 | -2.626791 | 2.304187 | 2.552583 | |||||||||||
| 0.5 | -2.551039 | 2.307011 | 2.554629 | -2.551039 | 2.307011 | 2.554629 | |||||||||||
| 0.5 | -2.551039 | 2.307011 | 2.554629 | -2.551039 | 2.307011 | 2.554629 | |||||||||||
| 0.5 | -2.551039 | 2.307011 | 2.554629 | -2.551039 | 2.307011 | 2.554629 | |||||||||||
| 0.1 | -2.551039 | 2.307011 | 2.469642 | -2.551039 | 2.307011 | 2.469643 | |||||||||||
| 1 | -2.551039 | 2.307011 | 2.554629 | -2.551039 | 2.307011 | 2.554629 | |||||||||||
| 0.2 | -2.551039 | 2.307011 | 2.184415 | -2.551039 | 2.307011 | 2.184414 | |||||||||||
Table 1: Comparison test results. Values of the skin friction, heat and mass transfer coefficients in present of suction.
The influence of magnetic field parameter on the velocity profile is shown in Figure 7. It was observed that the velocity profile depreciate monotonically as η increases. At any point on the boundary layer the velocity of a nanofluid increases with an increase in magnetic field parameter. The reason is that application of the magnetic field on the fluid flow region creates a Lorentz force which retards the fluid speed and as a consequence the velocity of the fluid within the domain of the boundary layer increases. The increases in the boundary layer thickness also increase with an increase on the strength of the applied magnetic field. Hence the surface velocity of the stretching sheet can be controlled by controlling the strength of the applied magnetic field. In Figure 8, shows the effects of radiation parameter on the temperature profile. We found that the influence of radiation parameter is directly proportional to the radiation parameter. It is noticed that an increase of the radiation parameter increases the temperature profile within the thermal boundary layer. The thickness of the thermal boundary layer thickness decreases with an increase of the radiation influence. In Figure 9, describe the influence of heat source (QH >0) in the boundary layer on the temperature profile. The presence of a heat source in the thermal boundary layer generates energy which causes the temperature of the nanofluid to increases. This increases in temperature yields an increase in the nanofluid fluid.
Figure 10 shows the effect of thermophoretic parameter on the concentration profile. It is noticed that both the plate surface and the nanofluid concentration increase when thermophoretic parameter increased. This results to an increase in concentration boundary layer thickness. As the value of thermophoretic parameter increases, the intensity of heat generation on the plate surface increases, the intensity of heat generation on the plate surface increases, which results to an increasing rate of convective heat transfer from the nanofluid on the surface of the plate. The rise in nanofluid concentration can be attributed to nanoparticle interaction connected to increasing thermophoresis. In Figure 11, we can see the influence of porosity parameter on the concentration profile. It was found that porosity parameter on the nanofluid concentration profile rise as the concentration profile increases. The reason is that increase in porosity increase the porous layer region and increase the concentration boundary layer thickness. It is seen also that, it’s generates the internal heat to the nanofluid flow, which will increase the concentration boundary layers.
Figure 12 shows the effects of velocity slip parameter on the velocity profile. We observed that the velocity profile decreases as the values of velocity slip parameter increases. With an increasing values of the velocity slip parameter, the nanofluid speed decreases monotonically. The reason is that the slip condition at the plate the speed of the fluid closed to the plate is positive values and the thickness of the momentum boundary layer decreases. As the slip parameter increases in magnitude it permits less fluid to slip past the plate, the flow gets decelerated for distance adjacent to the plate, the distance far away from the plate opposite the behavior. A similar trend occurred in temperature profile see Figure13. It was observed that for varying temperature with respect to thermal slip parameter. The profile shows that the wall temperature and thermal boundary layer thickness depreciate when the values of the thermal slip parameter increases. Also in case of concentration profile see Figure 14 the concentration profile and the concentration boundary layer thickness decreases when the values of the solutal slip parameter is increases. It decreases with an increase in solutal slip parameter.
The similarity solution in this work was considered to the problem of two dimensional flow of a steady laminar viscous, incompressible nanofluid over a permeable continuous stretching sheet in the presence of heat generation/absorption with velocity, thermal and solutal slip boundary conditions is studied semi-analytically. Using similarity transformations the involved partial differential equations of the problem are transformed into nonlinear ordinary differential equations and then solve by homotopy analysis method (HAM), by using MATHEMATICA 9.0. In our study the following conclusions can be drawn:
1. The velocity, temperature and concentration profiles decrease with an increase in exponential parameter.
2. The momentum boundary layer thickness of the velocity profile increase with an increase in magnetic field parameter.
3. The thermal boundary layer thickness of the temperature of the temperature profile increase with an increase in radiation parameter.
4. The thickness of temperature boundary layer increases with an increases in heat source parameter.
5. The thermophoretic parameter decreases with an increase in the concentration profile.
6. Increase in porosity parameter decreases the momentum boundary layer thickness and the velocity profile.
7. An increase in velocity, thermal and solutal slip parameters decreases the momentum, thermal and concentration boundary layer thickness and also their respective profiles.