Journal of Research and Development
Open Access

Iapetus Hypothetical Sub-Satellite Re-Visited and it Reveals Celestial Body Formation Process in The Primary-Centric Framework

Bijay K. Sharma^{* *}Correspondence: Bijay K. Sharma, Department of Electronics and Communication Engineering, National Institute of Technology, Ashok Rajpath, Patna-800005, India, Tel: +919334202848, Email:

Author info »

Introduction

In December 2004 Cassini spacecraft through its Imaging Science Subsystem (ISS) took close flyby high resolution imaging data of the outer Saturnian moons namely Phoebe and Iapetus [1].

Three features of Iapetus make it a class apart among the Saturnian moons. These are its present spin period of 79.3 days, the present oblate spheroid shape corresponds to the equilibrium figure of a hydrostatic body rotating with a period of 16 hours and its equatorial ridge [2]. Iapetus has the largest non-hydrostatic anomaly. Our Moon is the distant second [3,4].

Similar fossil bulge has been noted in Earth [5] and Mars [6].

Iapetus is the third largest moon of Saturn orbiting at a mean distance of 3.56 km × 10⁶ km on a slightly inclined prograde orbit. It is has two tone coloration. Leading hemisphere is dark called Cassini Regio whereas the lagging hemisphere is bright with the transition region have a graded change in coloration.

110° longitude arc of the equatorial bulge extends as a ridge system centered on the dark hemisphere side (Cassini Regio). Part of the ridge system rises more than 20 km above the surrounding plains. This ridge system has sections that have sets of isolated peaks (10 km high). Continuous ridge segments run more than 200 km in length and some sections have three parallel ridges. The ridge is cut by impact craters in some places. The ridge system as a whole is heavily cratered indicating that this is an ancient feature formed at the time of the core accretion formation of Iapetus.

The enigmatic walnut shaped Iapetus with an equatorial bisecting ridge in the dark hemisphere proved to be a complex puzzle. Both endogenic models and exogenic models [7] were proposed to explain the equatorial ridge. Because of the inherent difficulties of endogenic models [8], I will be concentrating on the exogenic model proposed by Levison, et al.

The leading hypothesis explaining the ridge system and the fossil bulge is as follows: About 2 to 5 M_y after the formation of Calcium-Aluminum-Inclusion (CAI) meteorite, Iapetus was formed by core-accretion in circum-saturnian accretion disk. Just as Iapetus formation was completed, it was impacted at glancing angle by comparable sized asteroid. This resulted in a circum- iapetian disk of dust and ice [9]. From this impact generated disk of dust and ice, Sub-Satellite (SS) was formed beyond its corresponding Roche’s limit which will be 2.495 R_Iap ~1.84 m × 10⁶ m assuming density of sub-satellite to be 1000 Km/m³ as has been assumed by Levison, et al.

This impact also led to an overall meltdown. This enabled Iapetus to acquire a new hydro-static equilibrium configuration in conformity with its rapid axial synchronous spin of 12.8 hours=orbital period of Iapetus at Roche limit of 1.27 × 10⁸ m=2.43 R_Sat (ρ_Sat/ρ_Iap)^1/3. The circum-Iapetian disk particles larger than micron size spiraled-in by Poynting-Robertson drag creating the equatorial ridge and remaining sub-micron particles were photo evaporated. The impact velocity of the disk particles would have been only ~300 m sec^-1 and mainly tangential to the surface of Iapetus. So it is reasonable to assume that they would not have formed craters but instead piled up on the equator to form the ridge. This was the exact scenario of Giant-impact in which our Moon was formed from impact-generated circum-terrestrial debris beyond the Roche’s limit (personal communication _arXiv:0805.0100v1 (astro=ph).

Subsequent to the impact, there was a rapid de-spinning of Iapetus from 13 hours to 16 hours by the tidal drag exerted by super-synchronous SS and a corresponding rapid cooling of Iapetus in first few hundred years. But SS will de-spin Iapetus only if SS is placed in super-synchronous orbit which requires that Roche’s limit of SS>inner Clarke’s orbit of Iap-SS system.

Because of rapid cooling, the stiffness or rigidity of the thick lithosphere of 15 Km-20 Km thickness [10] became sufficient to resist the relaxation of the global hydrostatic figure and continuous relaxation ceased and shape became “frozen” at a oblateness of 0.0455. To this day we see this oblatenes which is in conformity with 16 hours axial spin which must have been the case when Iapetus froze stiff [11].

Levison, et al. made this hypothesis more elaborate. They gave a dual role to the impact generated debris disk. According to them the debris disk puts an annular ring inside Roche’s limit and a comparable sub-satellite outside. The sub-satellite pushes the ring material to the surface of Iapetus and itself tidally evolves in an expanding spiral orbit de-spinning Iapetus only if SS is in super-synchronous orbit. Eventually the sub-satellite is lost, as it spirals out of the Hill Sphere of Iapetus, in a helio-centric orbit or it is recaptured by Iapetus and destroyed.

In this paper I will discuss the validity of Levison, et al. hypothesis in light of primary-centric mathematical framework.

The primary-centric world-view

The new perspective says that in any solar or exo-solar system or in any binary system.

• There are two Clarke’s orbits (inner Clarke orbit a_G1 and outer Clarke orbit a_G2).
• Here Clarke’s orbit is defined as the orbit where the two bodies are tidally interlocked with each other, orbit is circularized and components are synchronized meaning by no tidal dissipation is taking place and spin period of the primary=orbital period of the binary=spin period of the secondary. This I will refer to as triple synchrony state.
• Region beyond a_G2 is a forbidden zone for the secondary. The secondary can never enter the forbidden zone of orbits. If it does it will be deflected back.
• This gives criteria for determining gravitationally bound binary. If the secondary lies at or within outer Clarke’s orbit then it is a gravitationally bound binary else the two bodies are freely floating in space.
• Inner Clarke’s orbit is Gibb’s free energy maxima hence it is an orbit of unstable equilibrium. Slightest perturbative force causes the secondary to tumble short or long of a_G1.
• If the secondary tumbles short of a_G1 then it is in sub-synchronous orbit and the secondary gets trapped in gravitationally runaway collapsing spiral orbit. The secondary is destined to either coalesce with the central body or get tidally disrupted as it enters Roche’s zone. Hence this collapsing spiral orbit is also referred to as death spiral.
• If the secondary tumbles long of a_G1 it experiences an impulsive torque which I call gravitational sling-shot which imparts a large amount of rotational energy to the secondary. The secondary is launched on an expanding super-synchronous spiral orbit where it coasts on its own by virtue of its initial energy boost towards the outer Clarke’s orbit.
• Once in outer Clarke’s orbit it may remain stay put in that orbit or by third body perturbation it may be deflected back on a collapsing spiral orbit. The outer Clarke’s orbit is energy minima and hence an orbit of stable equilibrium.
• Only in inner and outer Clarke’s orbits the system is in truly Keplerian state that is the centrifugal force is exactly balanced by the centripetal force. In any other orbits there is a wee bit imbalance hence the secondary is in migratory phase.
• When the secondary to primary mass ratio ‘q’ is less than 10^-3, time constant of evolution τ=(a_G2-a_G1)/V_max, where V_max is the maximum outward radial velocity acquired by the secondary during gravitational sling shot phase, is of the order of G_y and evolution factor is a low fraction (€=(a-a_G1)/(a_G2-a_G1)).
• If the mass ratio is 10^-2 then time constant is M_y and evolution factor is in 0.5 neighbourhood. This will also depend on the age of the system.
• When the mass ratio is in the range of 2 × 10^-1 to unity then the time constant is in years/months/days and evolution factor is near unity no matter what the age is but not unity [12-15]. For 0.2 ≤ q ≤ 1, hydro-dynamic instability leads to the formation of the two components and for q<0.2, core-accretion process is the formative process for the secondary.
• Scoring a perfect score of unity evolution factor (€) will depend upon tidal circularization time-scale and tidal synchronization time scale. If thetwo time scales are within the observed age of the binary then the system will fall in triple synchrony state and the binary will score an unity evolution factor otherwise there will always be an offset from unity €.
• What this implies is that if the massratio is a large fraction larger than 0.2 then the secondary immediately falls into the near outer Clark’s orbit no matter what the age of the system is and if mass ratio is low then the secondary gradually evolves from inner to outer Clark’s orbit and the system has an evolutionary history and the present configuration will be a function of the time constant as well as the age of the system.
• If the secondary is infinitesimal mass fraction as the man-made satellite is then it remains in inner Clarke’s orbit and it has no evolutionary history.
• For strongly relativistic binaries such as double neutron star binaries, the near outer Clarke’s configuration is achieved on month/year time scale but final triple synchrony is never achieved due to gravitational radiation induced spin-in hence a finite offset with respect to unity evolution factor will always remain no matter what the age is. But this offset will be related to the strength of the relativistic system, measured by the mean rate of advancement of the periastron (apsidal rotation rate).

A binary system is amenable to theoretical analysis only if the spin-orbit-globe parameters are correctly and accurately known. Any mistake here will make the system untenable to mathematical analysis. High mass ratio binary falling in near outer Clarke’s Orbit had been identified by Zahn and Claret and Cunha. I quote Zahn in the following paragraph:

“Eventually the binary may settle in its state of minimum kinetic energy, in which the orbit is circular, rotation of both stars is synchronized with the orbital motion and the spin axis are perpendicular to the orbital plane. Whether the system actually reaches this state is determined by the strength of tidal interaction, thus by the separation of the two components, equivalently the orbital period. But it also depends on the efficiency of the physical process which is responsible for the dissipation of the kinetic energy.”

Materials and Methods

The simulation results of Levison, et al.

Iapetus has been assumed to be a regular satellite [16] which is formed by core accretion in the circum-saturnian debris disk [17] just at the time gas giants were forming in the first 30 M_y after the Solar-Nebula was born [18].

Just as our Moon was born in giant impact generated circum-terrestrial disc of debris, a Sub-Satellite (SS) was born in the impact generated circum-iapetian debris beyond Roche’s limit given by the formula:

Where;

ρ_Iap=1083 Kg/m³ and ρss=1000 Kg/m³ are the densities of Iapetian and the sub-satellite respectively. Substituting the numerical values in equation 1 we get:

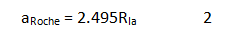
SS is formed beyond Roche’s limit=2.495 R_Iap irrespective of the mass of SS.

To be retained by Iapetus, the sub-satellite must remain in Hill’s sphere or Roche’s sphere of Iapetus. The hill radius of Iapetus is given by the following formula [19]:

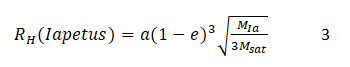
Substituting the numerical values of the parameters in equation 3 from Table 1 we get:

R_H=3,356,284.257 m

In Levison, et al., a formula best suited for orbital stability has been taken for negligible eccentricity:

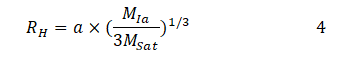
From this formula: R_H=36.235 m × 10⁶ m=49.26 R_Iap.

Saturn has slowed the spinning of Iapetus by tidal drag to match moon’s 79-day orbital year. Is this possible in 4.5 G_y. We will examine the despinning of Iapetus by an evolving sub-satellite in super-synchronous orbit. Dombard, et al., say, “Iapetus is the solar system’s moon with the largest hill sphere. It is the only moon far enough from its planet and large enough relative to its planet that a giant impact may be able to form a sub-satellite”.

Using swift-WHM integrator, Levison, et al., studied the evolving SS in super-synchronous orbit in Iapetus-centered frame with Saturn tidal effect included. For completeness the effect of Sun and Titan had been included. The effect of other saturnian satellites are atleast two orders of magnitude smaller than that of Titan hence they were ignored. The life-time of the particles dropped precipitously beyond 0.4 R_H suggesting that when SS evolves beyond this point it gets captured by Saturn. Hence stripping semi-major axis is taken as:

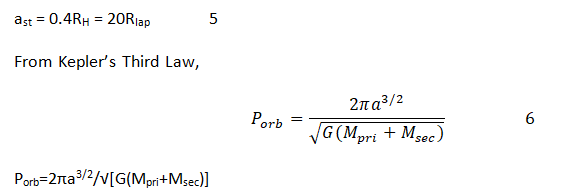
Using equation (6), a_st corresponds to 11.29 d,11.71 d,11.78 d,11.835 d and 11.84 d orbital period of SS for the mass ratios q=0.1, 0.021, 0.009, 0.001 and 0.0001 respectively. For q=0.1, SS never reaches ast. For q=0.1, SS gets locked-in the second Clarke’s orbit at a=5.38 R_Iap which is much earlier than a_st=20 R_Iap.

This means if SS survives to reach a_st, orbital period of SS will be 11 d~12 d. From this Levison, et al., has wrongly concluded that at stripping radius Iapetus spin period is 11 d~12 d. This would have been the case if a_st=a_G2 (second Clarke’s orbit) of Iap-SS binary. But this is not the case as shown in the following Table 1. For determining the spin period of Iapetus when SS reaches the stripping point, we have to follow the following algorithm:

ω/Ω=spin angular velocity of Iapetus/orbital angular velocity of the binary (Iap-SS) has to be determined.

ω/Ω=E×a^1.5-F×a² has to determine for a=a_st and values of constant E and F:

E= J_T/(B*C_Iap) and F=M_SS/(1+M_SS/M_Iap)*C_Iap

Where,

J_T=Total angular momentum of Iapetus and SS system.
C_Iap=Moment of inertia of Iapetus.

B=square root of (G(M_Iap+M_SS))

Since Ω is known therefore ω can be calculated. Following this algorithm the values of spin period of Iapetus derived at stripping radius is given in Table 1.

Table 1: Spin periods of Iapetus when SS reaches a_st.

Hence for different mass ratios, Iapetus-SS binary will at best manage to spin down Iapetus to 1.5 d spin period but never more than that. Remaining de-spinning will be left to Saturn.

But now Saturn will do its de-spinning job more efficiently. Starting with the assumption of constant Q/|k₂| and using the standard timescale, de-spinning time from 16 hours to 79.33 days is given by:

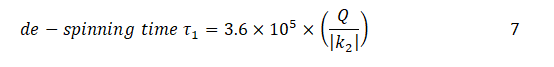
De-spinning time τ₁=3.6×10⁵ × (Q/|k₂|)

Where;

Q=Dissipation factor
k₂=Love Number

Q/|k₂|=Decreasing function of spin rate hence Saturn now de-spins Iapetus faster to 79.3 days spin period within solar system age of 4.5 G_y.

If Saturn was alone required to de-spin from 16 hours to 79.33 days, then equation (7) with constant Q/|k₂| yields nominally a time of 36 G_y for density ρ_Iap=1000 Kg/m³. Therefore the need has arisen for invoking the presence of SS in super-synchronous orbit to assist Saturn in de-spinning over the requisite range in solar time-scales.

From equation (6), we get the formulation for triple synchrony orbit which has been referred to as synchronous orbit by Levison, et al.:

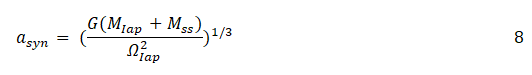
Where;

M_SS=mass of the sub-satellite (SS) and Ω_Iap=ω_SS=ω_Iap;

(syn.orbit) a_syn=[G(M_Iap+M_SS)/Ω_Iap²]^1/3=Triple Synchrony Orbit

Triple synchrony in a binary is equivalent geo-synchronous orbit in E-M system. In triple synchrony:

Spin_primary (ω_P)=Spin_secondary (ω_S)=Orbital(Ω) of binary.

Synchronous orbit implies:

Spin_secondary(ω_S)=Orbital (Ω)of binary.

Our moon or anybody in captured rotation is in synchronous orbit. Here secondary is locked with primary but primary is not locked hence tidal dissipation in primary is taking place.

In triple synchrony, primary and secondary are mutually interlocked and there is no tidal dissipation. The orbits are absolutely circularized and periods are absolutely synchronized. There will be absolutely no repetitive stretching and squeezing and hence no dissipation.

There is a triple synchrony in inner as well as in outer Clarke's orbits. In both orbits equilibrium of centripetal and centrifugal forces exists as assumed in Kepler three laws. But inner Clarke's orbit is highly unstable equilibrium for significant mass ratios i.e., from q=0.0001 to q=0.19 as shown in SOM-Appendix B. For q=0.0001 to q=0.19, inner Clarke's orbit corresponds to energy maxima and there is finite time constant of evolution from inner to outer Clarke's orbit varying inversely as some power of 'q'. From q=0.0001 to q=0.19 time scale of evolution varies from G_y two years.

For q less than 0.0001, energy maxima gradually flattens out, time scale of evolution increases with decreasing mass ratio. As q approaches an infinitesimal number as in the case of man-made satellite, time scale becomes infinite, energy flattens out completely, outer Clarke's orbit becomes infinite and man-made satellite never evolves out of this orbit though it remains vulnerable to Poynting-Robertson drag as well as to radiation pressure.

In contrast outer Clarke's orbit is an energy minimum shown. Hence it is a stable equilibrium configuration. Within q=0.0001 to 0.19 secondary is always evolving from inner to outer Clarke's orbit and secondary has an evolutionary history with a decreasing time-constant of evolution as 'q' increases. Above q=0.19 and much below q=0.0001, secondary for all practical purposes has no evolutionary history. Below 0.0001 the secondary remains stuck at Inner Clarke’s Orbit and above 0.19 the secondary immediately falls into outer Clarke’s configuration.

1^st col and 2^nd col in Table C3. We obtain Table 2 for SS synchronous orbit. I am retaining the nomenclature of Levison, et al., but with the above caveat.

Table 2: Sub-satellite synchronous orbit for different mass ratios.

Let the semi-major axis of SS be a_SS.

If a_SS<a_synSS, then SS is in sub-synchronous orbit where through tidal pull it spins-up the Iapetus-SS system and SS itself spirals-in to the central body Iapetus.

If a_SS>a_synSS, then SS is in super-synchronous orbit where it de-spins the Iapetus-SS system. In this case SS through tidal drag de-spins Iapetus and itself spirals out in an expanding orbit until it reaches the lock-in point or it is stolen by Saturn’s hill sphere.

In simulation programme, SS is placed in super-synchronous orbit at 3 R_Iap and hence it is de-spinning Iapetus and receding from Iapetus in all cases except q=0.8. Simultaneously Saturn is also spinning down Iapetus hence, according to equation 8, a_syn is expanding. If before reaching a_st, a_syn sweeps past SS then SS will fall in sub-synchronous orbit spinning up the whole system and in the process spiraling in to its sure doom.

Levison, et al., considered three scenarios:

Scenario 1 where 0.021<q<0.04

Scenario 2 where 0.006<q<0.021

Scenario 3 where 0.0001<q<0.006

In each scenario, four geo-physical models have been considered:

• Constant internal viscosity model.
• Castillo-Rogez LLRI model.
• Robuchon, et al. 0.04 ppbAl model.
• Robuchon, et al. 72 ppbAl model.

Scenario 1: 0.021<q<0.04

As shown in Figure 1, here SS reaches the synchrony state much earlier than the stripping semi-major axis a_st=20 R_Iap and it gets locked at that point. Eventually the despinning of Iapetus by Saturn allows the synchronous orbit a_syn to sweep past the synchronous SS. At this point it falls in sub-synchronous orbit and it spirals-in to be merged with Iapetus at re-impact point.

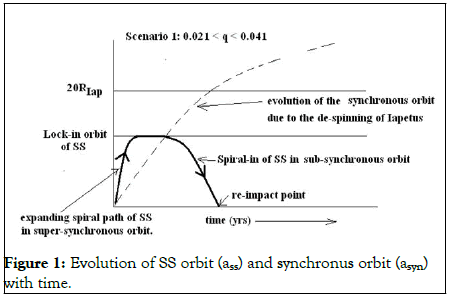
Figure 1: Evolution of SS orbit (a_ss) and synchronus orbit (a_syn) with time.

Let the time of de-spinning due to Saturn alone=T_de-spinO

Let the time of de-spinning dueto Saturn and SS combined=T^*_de-spinO.

In this particular scenario SS does not help in de-spinning because of re-impact. Instead it spins-up the Iapetus during spiral-in phase. Hence here:

T^*_de-spinO>T_de-spinO

Re-impact depends on mass ratio. For high mass ratio, the re-impact time is 1G_y whereas for low mass ratio the re-impact time can be as high as 1T_y. This scenario has very little dependence on the geo-physical models. At the re-impact it definitely can give rise to equatorial ridge. But since the re-impact time is so recent and the equatorial ridge is so ancient that it is unlikely that this could have formed the ancient ridge. So this mass ratio is ruled out in our present de-spinning scenario.

Scenario 2: 0.006<q<0.021

Here as shown in Figure 2, SS manages to de-spin Iapetus and eventually it is stripped away by Saturn. This considerably shortens the de-spinning time as much as by a factor of 10 in case of q= 0.02. The shortest de-spinning time is 500 M_y.

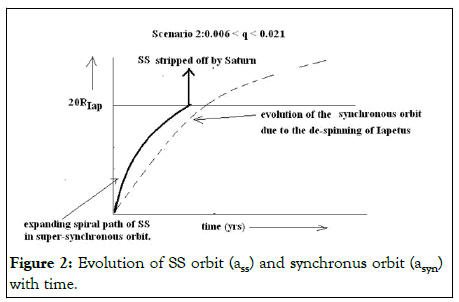
Figure 2: Evolution of SS orbit (a_ss) and synchronus orbit (a_syn) with time.

There is no re-impact hence this scenario has no contribution to the formation of the ancient equatorial ridge but it definitely assists Saturn in de-spinning Iapetus from 16 hours to 79.33 days within the age of our solar system.

Scenario 3: 0.0001<q<0.006

Since the mass ratio has become insignificant the expanding semi-major axis of SS unfolds at a much larger time scale than that of the synchronous orbit expansion hence the expanding semi-axis curve of SS is intersected by the expanding synchronous orbit earlier than the stripping point as shown in Figures 3 and 4. As soon as the expanding semi-axis curve of SS is intersected by the synchronous orbit curve, SS spirals-in again spinning-up the system.

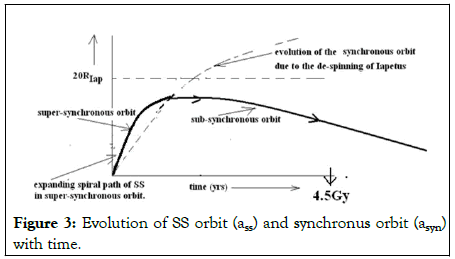
Figure 3: Evolution of SS orbit (a_ss) and synchronus orbit (a_syn) with time.

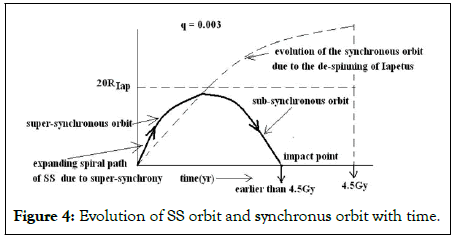
Figure 4: Evolution of SS orbit and synchronus orbit with time.

In Figure 3, we have 0.0001<q<0.003 scenario. Here the spiral-in SS does not re-impact within the age of the solar system. In this particular scenario through simulation it is claimed that de-spun process is speeded up but there is no re-impact for the formation of the equatorial ridge. Therefore this case is totally ruled out from our probable scenario list.

In Figure 4, we have the simulation for q=0.003. In this scenario through simulation it is claimed that de-spun process is completed in 2.25 G_y but there is a re-impact which could lead to the formation of a recent equatorial ridge but the actual Iapetian ridge is as ancient as its formation hence this scenario is also ruled out.

Conclusion of simulation experiments

Through simulation it is claimed that SS with a mass fraction of q=0.021 to 0.04 increases the de-spun time hence this scenario can be excluded. SS with a mass fraction of q=0.006 to 0.021 can play a positive role in bringing the de-spun time within the solar system age constraint of 4.5 G_y. For q=0.02, de-spun time is claimed to be completed within 500 M_y. Again SS with mass fraction within the range 0.0001 to 0.006 can help improve the de-spun time but for mass ratios 0.003 to 0.006, causes a recent re-impact leading to a fresh ridge which is contrary to the ancient nature of the existing ridge. Hence these scenarios are ruled out.

So according to Levison, et al., the most preferred scenario is that a SS of q between 0.006 to 0.021 formed from the impact generated circum-iapetian disk beyond Roches’ limit placed in a super-synchronous orbit helped de-spin the Iapteus-Saturn system from 16 hours to 79.33 days within the solar system age and the impact generated debris within the synchronous orbit spiraled-in to form the ancient poke-marked equatorial ridge of Iapetus.

In the following sections we will test the above hypothesis on the touch-stone of primary-centric world view. Before we proceed we will briefly dwell upon the primary-centric world view.

Evolutionary history of Saturn-Iapetus system in primary-centric framework

According to primary-centric formulation any binary system has two Clarke’s orbits a_G1 and a_G2 where triple synchrony is achieved namely:

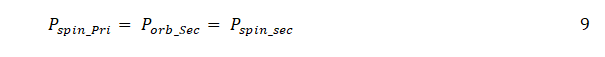
So initially when Iapetus was formed beyond Roches limit at about 1.28 × 10⁸ m, saturnian moon was automatically at super-synchronous orbit since a_G1 of Iapetian-Saturn system is at 1.1 × 10⁸ m.

If we take the globe-orbit-spin parameters of Iapetus-Saturn system, then in inner Clarke’s orbit, the secondary would be orbiting and spinning in 0.43 d=10.3 hours, the primary would also be spinning at 10.3 hrs. But since Iapetus was formed beyond Roches limit=1.28 × 10⁸ m hence its spin period=orbit period=12.971 hours initially. At the time its accretion was completed it must have been in molten stage due to the heat of accretion and due to radiogenic heating. In this molten stage it acquired a hydro-static equilibrium shape of an Ellipsoid corresponding to 12.971 h.

At this point Iapetus must have experienced an impulsive torque due to gravitational sling shot which launched Iapetus on an expanding spiral orbit (personal communication arXiv: 0805.0100v1 (astro=ph). Because of the expanding spiral orbit, the whole binary system started being de-spun and the primary-secondary went out of triple synchrony. There was tidal stretching and squeezing of Saturn due to Iapetus. This tidal deformation led to tidal heating of Saturn since it is anelastic.

Iapetus remained in synchronous state meaning by:

In synchronous state, Iapetus is permanently instretched state hence it experiences no tidal heating.

The ratio of (orbital period of Iapetus/spin period of Saturn)=ω/Ω started growing according to the formulation below:

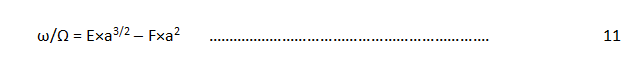
Where;

E=J_T/(BC_Sat)=8.680510156 × 10^-13 m^-3/2
F=(M_Iap/(1+M_Iap/M_Sat))(1/C_Sat)=2.177335304 × 10^-21 m^-2

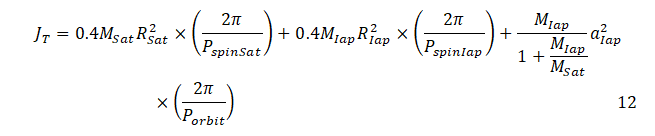
J_T=1.3983260521 × 10³⁸ Kg.m².sec^-1
And C_Sat=0.4M_SatR_Sat²=8.266959631 × 10⁴¹Kg.m²
And B=√[G(M_Sat+M_Iap)]=194.857615 × 10⁶ (m^3/2/sec)

Therefore;

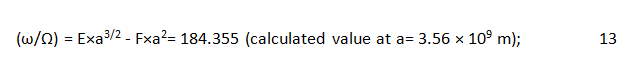
Present observed value (ω/Ω)=P_{orbit_Iap}/P_{spin_Sat}=184.467

Where;

Our present observed P_orbit of Iapetus=79.33 d and
P_{spin_Sat}=0.43 d.

In 1.68 M_y, Iapetian’s orbit expanded from 1.28 × 10⁸ m (this is the orbit just beyond Roches’ limit) to 1.46 × 10⁸ m and its orbital period de-spun from 12.8 hours to 16 hours. As it was being de-spun, the ellipsoidal shape relaxed to spheroidal shape and kept adjusting according to the dynamic hydro-static equilibrium conditions.

In first few hundred years period due to rapid cooling, 15-20 km thick lithosphere of Iapetus became stiff enough to prevent further relaxation to the dynamically varying hydrostatic equilibrium spheroidal Maclaurian shape. Hence the hydrostatic shape corresponding to 12.971 hours should have got frozen and but the ‘fossil bulge’ we see today has an oblateness of 0.0455 (equatorial diameter is 1492 Km and polar diameter is 1424 Km) corresponding to 16 hours spin-period. This is known as non-hydrostatic equilibrium anomaly.

Without SS we must see a larger anomaly then what is being presently seen therefore, to this scenario as hypothesized by Levison, et al. I add an impactor right after the accretion of Iapetus. This impactor could have been a planetary embryo of any size and mass and this impact could have been similar to the Giant impact of earth by a Mars-size planetesimal.

The impact of Iapetus achieved the following objectives:

• It caused a general meltdown leading to new hydrostatic configuration in conformity with the rapid spin.
• It produced impact generated debris in the equatorial plane of Iapetus.
• The debris within Roche’s limit, spiraled-in by Poynting-Robertson drag leading to the formation of the equatorial ridge surrounding the whole globe of Iapetus and subsequently half of the ridge got eroded off by meteoritic impact.
• The debris outside the Roche’s limit accreted to form a sub-satellite which played a role in de-spinning Iapetus. The formation of a sub-satellite seems to be a very likely event because Iapetus is the solar system’s moon with the largest Hill sphere. It is the only moon far enough relative to its planet that a giant-impact may be able to form a sub-satellite.
• The second rapid cooling of Iapetus in first few 100 years after the second impact helped fossilize the equatorial bulge which we witness to this day.

Homogenous body can have (a-c)=34.5 Km with a spin period of 16 hr ± 1 hr but a differentiated body with a core of 3510 Kg/m³ will need a faster spin of period=14.7 hr. Here ‘a’ and ‘b’ are the semi-axes in equatorial plane and ‘c’ is the semi-axis along polar axis.

This fifth point places a further constraint on the hypothetical SS.

The inner Clarke’s orbit of Iapetus is at 1.1 × 10⁸ m. This corresponds to orbital period=spin period of Iapetus=10 hours. The Roches’ limit=1.27 × 10⁸ m. Just beyond this point Iapetus formed and it had orbital period=spin period=12.971 hours because it was in captured rotation. But the fossil bulge we see corresponds to 16 hours (this corresponds to ‘a’=1.46 m × 10⁸ m) if Iapetus is homogeneous. The same fossil bulge corresponds to 14.7 hours (this corresponds to ‘a’=1.39 × 10⁸ m) if Iapetus is differentiated with a core of 3510 Kg/m³. In the Table 3 below, the time taken to achieve expanded semi-axis from 1.27 × 10⁸ m to 1.46 × 10⁸ m is given.

Table 3: De-spun time (calculated from primary-centric calculations) from initial 12.971 hrs to the present spin period and to two different spin periods corresponding to the fossil bulge of a homogeneous body and differentiated body.

Inspecting the Table 3, it is obvious that SS should be there to assist Saturn in rapidly de-spinning Iapetus so that within few hundred years non-hydrostatic equilibrium anomaly is recorded for the posterity. Without SS the fossil bulge should be much larger than what is seen today. Presence of SS or any other plausible factor should reduce the de-spun time from 1.6 M_y to few hundred years because Iapetus is nearly a homogeneous body.

As we have already mentioned in section 2 that two Clarke’s orbits are analogous to the two geo-synchronous orbits in earth-moon system and the two components of the binary are tidally inter-locked in these two orbits and Kepler’s third law strictly apply in these two orbits only. In all other orbits there is a wee bit imbalance between centripetal and centrifugal force resulting in a residual radial velocity either directed inward leading to collapsing spiral path or directed outward leading to expanding spiral path.

The secondary is captured or formed by accretion at inner Clarke’s orbit. The inner Clarke’s orbit is unstable equilibrium orbit. Hence any perturbation such as solar wind, cosmic rays or photo-radiation pressure is sufficient to make the secondary tumble from its inner Clarke’s orbit. The secondary may tumble out and fall short of a_G1 or fall long of a_G1. This leads to two distinctly different evolutionary histories of the secondary.

If it falls short of a_G1 the secondary is trapped in sub-synchronous orbit and if it falls long of a_G1 the secondary is launched by gravitational sling shot impulsive torque in super-synchronous or extra-synchronous orbit (personal communication: arXiv:0805.0100v1(astro=ph)).

The evolutionary history of the secondary trapped in sub-synchronous orbit.

In sub-synchronous orbit, ω/Ω is less than unity and secondary’s tidal torque is spinning up the primary hence secondary is transferring momentum and energy to the primary. There is tidal heating also due to tidal deformation of the two components of the binary. This leads to a gravitational runaway collapsing orbit. Here the secondary is doomed to complete destruction either by impacting the primary or being pulverized as soon as it enters Roche’s limit. Hence this is known as a death spiral.

This final merger in a death spiral takes place in every binary system only the scale of the impact varies.

• In satellite-planet merger the impact will be of the scale several orders of magnitude greater than what was seen in Shoemaker Levy 9’s Comet impact on Jupiter.
• (Foot note; SL9 got captured by Jupiter in 1960’s and it was launched on death spiral/collapsing spiral. It was moving in a highly elliptical orbit and in July 1992 its collapsing elliptical orbit grazed passed the Roche’s limit at 11,000 Km from the center of Jupiter. This led to the fragmentation of SL9. These fragments eventually collided with the planet’s surface between July 16 and July 22 1994).
• In planet-planet hosting star merger, there are clear accretion signatures in form of IR excess and 7Li enrichment [20,21]. There can be tidal heating and bloating of the planet size as seen in HD20458b [22]. WASP-18 b is racing to a similar fate of doomsday [23]. HD82943 has already engulfed its planet [24].
• In star-super massive black hole at the center of a galaxy interaction we have only recently observed ‘a possible Relativistic Jetted outburst from a massive black hole fed by a tidally disrupted star’ [25].

The evolutionary history of secondary launched on super-synchronous orbit.

In a super-synchronous orbit, ω/Ω is greater than unity hence tidal drag of secondary is pulling back and tidal brake is being applied to the rapidly spinning primary. Initially for a short period of time when tidal heating is negligible due to near triple-synchrony condition the system is conservative but as it falls out of triple-synchrony the deformation becomes considerable to make the system fully dissipative and tidal heating ensues. During the conservative phase when energy and momentum both are being transferred from the primary to the secondary, an impulsive torque is applied generated by the gravitational sling-shot effect. This torque radially accelerates the secondary to maximum velocity (V_max). Once the impulsive torque has decayed, the secondary coasts on its own on an expanding spiral path with the rotational energy acquired during the conservative phase of application of gravitational sling shot impulsive torque to the secondary.

While the secondary is coasting on its own, Saturn-Iapetus system is being despun.

• The primary is being despun by the tidal brake.
• The secondary is receding and is also being despununtil radial velocity becomes zero.
• This non-Keplerian journey of the secondary terminates at a_G2.
• The secondary cannot move beyond a_G2.
• At a either the secondary remains stay put as Charon is stay put around Pluto or the secondary is deflected back into a collapsing spiral orbit as moon will be deflected back in future when it reaches a_G2 [26].

Primary-centric formulation of Saturn-Iapetus-SS system

The globe-orbit-spins parameters of Saturn-Iapetus system. Using these parameters we determine the kinematic parameters of the Saturn-Iapetus binary system and we carry out the primary-centric analysis of Saturn-Iapetus System. In Figure 5, we give the evolution of synchronous orbit of SS (equation 8) with time for different values of q=mass ratio of SS and Iapetus.

The thick curve in Figure 5 corresponds to q~0. The dotted and dashed curves alternatively correspond to q=0.001, 0.021, 0.04, 0.2, 0.4 and 0.8 respectively.

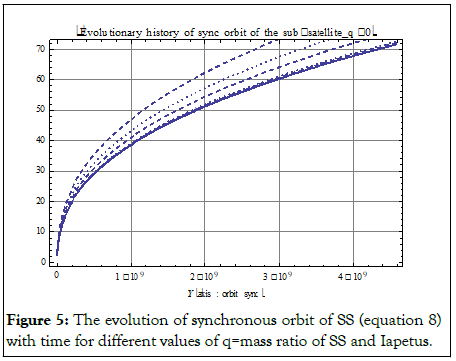
Figure 5: The evolution of synchronous orbit of SS (equation 8) with time for different values of q=mass ratio of SS and Iapetus.

Within solar system’s age (4.5 G_y), minimum range of expansion of synchronous orbit is from 2.55 R_Iap to 71 R_Iap for q~0 and maximum range is from 3.11 R_Iap to 86.44 R_Iap for q=0.8.

The typical values of de-spinning obtained through recent studies.

In any binary system, in super-synchronous orbit the primary and secondary both are being despun for prograde systems. This despinning can be calculated using equation A.15 (spin to orbital angular velocity equation) and Kepler’s third law equation 6.

Using equation 6, the orbital angular velocity of the secondary is calculated at a_G1 a_present and at a_G2. Since in all planet-natural satellite systems, the secondary is in captured rotation hence P_orb is equal to P_{spin_sec}. Hence equation 6 also yields the despun values of spin periods of the natural satellites. Table 4 gives initial spin period and the present despun values of our Moon, Charon- the moon of Pluto and Iapetus-the moon of Saturn.

Table 4: Spin periods of Moon, Charon and Iapetus at inner Clarke’s orbit, at the present day orbit and at the outer Clarke’s orbit in future.

From Table 4 we can see that the de-spinning of Iapetus is unusually large. Even the extra solar systems studied do not give the kind of de-spinning as seen in Saturn-Iapetus system.

Spin period of sun and Planet Hosting Star (PHS) at the fiducial age of 650 M_y and the present time

Zoghbi have studied the spin period of 443 Planet Hosting Stars (PHS) both at the present age and at 650 M_y after the birth of the respective solar nebula. They have assumed that the orbital parameters of our solar system and extra-solar systems must have stabilized in 650 M_y. Hydae star group was born 650 M_y before the present hence their star’s rotation period will indicate what our Sun or PHS rotation period could have been 650 M_y after their birth. The B-V index of our Sun or PHS was matched with that of Hydae stars and the corresponding spin-period selected. Our Sun’s B-V index matches the B-V index of Star VB-15 of Hydae star group hence ~8 days was chosen as the spin period of our Sun at an age of 650 M_y and 25.38 days at the present time i.e., at the age of 4.56 G_y. In a similar manner the spin periods of 433 PHS were cataloged in Table 3 of the reference Zoghbi. In Table 5 of the present text a few selected PHS spin period at the fiducial age of 650 M_y and at thepresent age is catalogued.

In all cases with a few exceptions there has been a de-spinning of PHS hosting prograde planets and there are cases in which there has been large de-spinning as can be seen by inspection but the cases which have large de-spinning are Post-Main Sequence (PMS) stars which can be identified by their large diameters.

MS progenitors of these Giants and sub-giants have only tidal braking responsible for de-spinning but in giant branch (asymptotic giant branch or red giant branch) stage stellar loss and magnetic braking affects the evolutionary history.

So Table 5 cannot be true representative of de-spinning of the primary due to tidal drag in super-synchronous cases.

Table 5: Spin period of sun and PHS at the fiducial age of 650 M_y and the present time. (Col.1_Age (G_y), Col.2_BV index, Col.3_P_{spin_Initial} (d), Col.4_P_{spin_present} (d), Col.5_ radius of sun or PHS (× R_Sun),Col.6_mass of sun or PHS (× M_Sun), Col.7_mass of planet (× R_Jup),Col.8_References].

Table 5 has inconsistencies also such as COROT-11. COROT-11 from BV index matching has an initial stellar spin period of ‘9.36 d’ 650 M_y after the formation of solar nebula but tidal dissipation consideration gives initial stellar spin period of ‘1.4 d’ and primary centric consideration gives initial stellar spin period of ‘1.7 d’. According to primary-centric considerations in 2 G_y, PHS has de-spun from 1.7 d to 1.73 d.

This clearly establishes that some other mechanism has to be invoked in Saturn-Iapetus system whereby Iapetus may be de-spun from 13 hours to 16 hours in first hundred years and to 79 d subsequently in solar system time framework.

The origin of the sub-satellite

Iapetus is not a captured body but an accreted body formed in the circum-saturian disk just at the time gas giants were forming in the first 10 M_y after the solar-nebula was born. Just as our Moon was born in giant impact, a sub-satellite was born in the impact generated circum-iapetian debris beyond Roche’s limit where from (1) Roche’s limit=2.495 R_Iap.

Where;

ρ_SS is the density of the sub-satellite with numerical value of 1000 Kg/m³. Substituting the numerical values in equation 14 we get:

From equation 8, we get the formulation for synchronous orbit of SS with respect Iapetus:

Where;

M_SS=mass of the satellite which is decided by the mass ratio ‘q’.

This synchronous orbit is the same as inner Clarke’s orbit of primary centric frame work for 0<q<0.006 as seen from Table 6 which has been adapted.

Table 6: The comparative study of inner Clarke’s Orbit and the sum of Iapetus and SS radii for different mass ratios ranging from q=0.0001 to q=1 and its implication for the formation process.

From mass ratio (q) insignificant magnitude to 0.006 there is a remarkable convergence between the keplerian framework and primary-centric framework. At mass ratios greater than 0.006 the two frameworks start diverging. This divergence becomes more pronounced as ‘q’ approaches unity. At q=0.3, there is a dramatic change in celestial body formation. At q=0.3 and more inner Clarke’s orbit becomes less than (R_Iap+R_SS). Physically this means that inner Clarke’s orbit becomes fictitious and the celestial pair is not formed by core accretion path but by hydrodynamic instability and on a time scale of months and years the celestial binary falls in outer Clarke’s configuration. This brings out the inadequacy of Keplerian kinematics when tidal interaction starts dominating.

Inspection of the Table 6 shows that for mass ratios 0.0001<q<0.006, inner Clarke’s orbit (a_G1)=a_synSS and a_G1>(R_Iap+R_SS). This means that SS has formed by normal core-accretion process at a_G1. SS is formed at a_G1 and launched on super-synchronous orbit.

For 0.006<q<0.2, a_G1>(R_Ia+R_SS) hence core accretion process is the legitimate pathway for the formation of SS. Whereas for mass ratios 0.2<q<1.0, inner Clarke’s orbit (a_G1) is less than (R_Ia+R_SS). This means the binary components have been formed by hydro-dynamic instability [27] falling in outer Clarke’s configuration well beyond Roche’s limit. In the whole range from 0.2<q<1.0 there is no evolutionary history. By hydrodynamic instability the two components are formed and they, in a very short time scale months/years, acquire the stable configuration corresponding to the outer Clarke’s orbit as is the case in double pulsar (MOON-D-12-000653), pulsar-star, brown-dwarf pair or star+brown-dwarf pair\citep(sha11). The spin of the primary=the spin of the secondary=the orbital period of the binary are at a steady state value or the binary is asymptotically approaching this triple synchrony condition. There is neither de-spinning nor spin-up in hydrodynamic instability scenario.

Right from its inception: Ω_Iap=orbital angular velocity of Iapetus=spin angular velocity of Iapetus=ω_Iap.

Since Iapetus is in captured rotation right from the beginning of its formation hence as it has spiraled out, its orbital period and spin period have increased synchronously. Hence in Iapetus-SS binary system, a_syn has given in (8) has continuously expanded with the evolution of Iapetus. But as already seen in Table 6, a_syn is not the correct formalism of Binary Kinematics for q>0.006. So in the present analysis we will look at the evolution of a_G1SS rather than the evolution of a_syn as has been doneby \citet (lev11).

Iapetus has de-spun from 12.971 hours to 16 hours and subsequently to 79.3 days over a period of 4.5 G_y so has a_syn expanded from 2.558 R_Ia to 2.938 R_Ia to 71 R_Ia for q~0 in Keplerian framework over the same period of 4.5 G_y.

At the time sub-satellite is fully formed it is at the synchronous orbit=inner Clarke’s orbit where it is in triple-synchrony state [28-32].

Therefore;

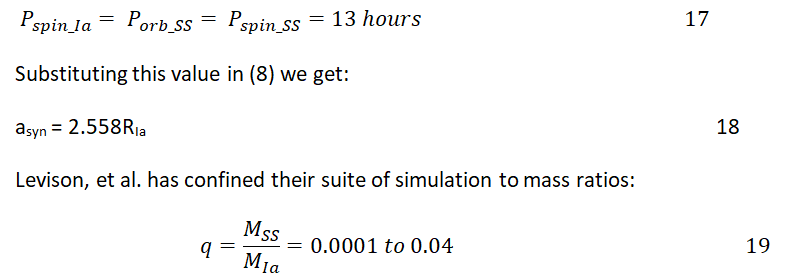
In this paper through primary-centric analysis, the physics of simulated results obtained by Levison, et al., will be elucidated and it will be further clarified why we leave out the consideration of q in the region of 0.04 to 1 and region below 0.0001 [33].

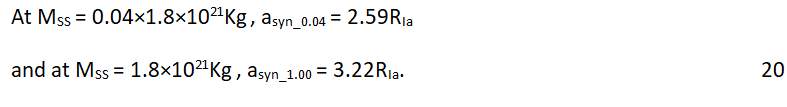
From (17) and (18) it is evident that placement of SS at 3 R_Iap for q ≤ 0.04 makes SS super synchronous hence SS helps de-spin the system and for q=1, SS becomes sub-synchronous and SS spins up SS-Iapetus binary system.

For q ≥ 0.04, we will have to place SS in suitably larger orbit than its respective a_syn in order to get the de-spinning effect [34-38].

Sub-satellite time-scales of evolutionary history for different mass ratio from primary-centric formulation

We will consider all the mass ratios from q=0.0001 to q =0.8. Through primary centric analysis, the two Clarke orbits for SS for mass ratios from q=0.0001 to q=0.8 are tabulated in Table 7. Time constants of evolution are included in the Table 7. Time constants have not been calculated. They have been estimated on the basis of previous studies given [39-42].

Table 7: The two Clarke’s orbits semi-major axis for q=0.0001 to q=0.8 and τ=time constant of evolution.

Table 7 very clearly brings out the all comprehensive nature of primary-centric framework. For in-significant mass ratios there is only one triple synchrony state as also predicted by Keplerian framework. For man-made geo-synchronous we get only one geo-synchronous orbit at 36000 Km above the surface of Earth in both frameworks\citep (sha08). For mass ratios greater than 0.2 upto unity again there is only one Clarke’s Orbit and that is outer Clarke’s orbit. Both frameworks predict this triple synchrony orbit not identically but in very close proximity as can be seen by the close examination of. The inner Clarke’s orbit is less than the sum of equatorial radii of the primary and secondary and hence it is untenable [43-46].

It is because of these observations that I say that primary-centric world view is a more complete and accurate description of binary kinematics as well as their formation process. This is because it includes the tidal effect where it is dominant. On the other hand since Copernican World view has not considered the tidal effects it completely fails to account for the binary kinematics between 0.0001<q<0.3.

Close scrutiny of Table 7 shows that there is a qualitative change in the evolutionary history of SS at q=0.021.

For the cases q>0.021, the second Clarke’s orbit is less than the stripping semi-axis i.e., a_G2<a_st and SS has no possibility what so ever of entering Saturn’s hill sphere.

For cases q<0.021, a_G2>a_st and SS has the possibility of entering Saturn’s Hill sphere. We will study these two cases in detail.

Results

Evolutionary history of SS for different mass ratios and the accompanying despinning of Iapetus according to primary-centric formulation.

Detailed kinematic model based calculations for sub-satellite of different mass ratios have been worked out and their contribution towards de-spinning of Iapetus and towards the formation of ancient equatorial ridge has been evaluated. Here we state the outline of the results [47-50].

We can divide the mass ratio q=0.0001 to 1.0 in three zones:

• From 0.2<q<1.0 is the zone where SS forms by hydrodynamic instability and gets locked at outer Clarke’s orbit on a time scale of years. The outer Clarke’s orbit is at 3.88 R for q=1.0 which corresponds to an orbital period 17.2 hours. The outer Clarke’s orbit is at 3.2 R for q=0.3 which corresponds to an orbital period of 15.95 hours. At q=0.3, ‘Iapetus+SS’ immediately assume a stable configuration with orbital period of SS=spin period of SS=spin period of Iapetus ~16 hours. In this case Iapetus is rapidly de-spun from 13 hours to 16 hours and gets frozen at this hydrostatic equilibrium ellipsoidal shape.
• From 0.006<q<0.2, the SS forms by normal core accretion process but gets trapped in death spiral right from the beginning because a_G1<a_{_synSS} as seen in Table 4. In this zone SS is destined to spiral-in and impact Iapetus. It does not contribute to de-spinning and does not contribute ancient ridge in most cases.
• From 0.0001<q<0.006 is the third zone where SS forms by normal core accretion process and a_G1=a_{_synSS}. Therefore SS is launched on a super-synchronous orbit and therefore may significantly de-spin Iapetus and eventually be captured by Saturn.

The evolutionary history of SS for q=0.4

Let us consider the case q=0.4. This is the case of hydro-dynamic instability. Hence after the second impact in months-years, Iapetus-SS pair is formed in stable equilibrium configuration at outer Clarke’s orbit with orbital period of SS=spin period of SS=spin period of Iapetus ~16 hours with year time scale. Almost instantaneously Iapetus is de-spun from 13 hours to 16 hours and, in few hundred years because of high thermal conductivity, 16 hours hydro-static equilibrium ellipsoidal shape is frozen for the posterity [51-54]. Subsequently because of de-spinning of Iapetus by Saturn, Sub-satellite’s synchronous orbit expansion sweeps past the contemporary orbit of SS at 1.68 M_y and SS as abruptly spirals-in and impacts into Iapetus leaving an equatorial ridge. This could be as ancient as seen today by Cassini mission. This scenario is quite plausible and the remaining de-spinning is done by Saturn (Figure 6).

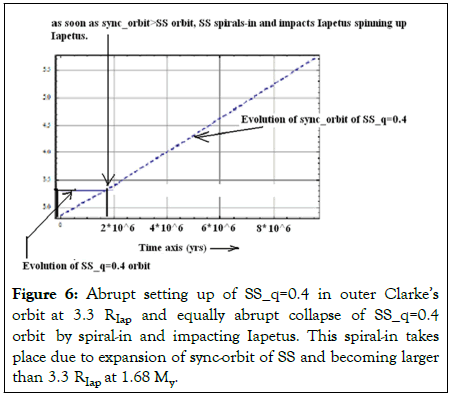
Figure 6: Abrupt setting up of SS_q=0.4 in outer Clarke’s orbit at 3.3 R_Iap and equally abrupt collapse of SS_q=0.4 orbit by spiral-in and impacting Iapetus. This spiral-in takes place due to expansion of sync-orbit of SS and becoming larger than 3.3 R_Iap at 1.68 M_y.

The evolutionary history of SS for q=0.1

SS for q=0.1 has formed through core accretion process hence it has an evolutionary history. From Table 4, ‘a_sync=2.64 R_Iap’>‘a_G1=2.56 R_Iap’ therefore SS at q=0.1 is doomed to be trapped in death spiral and impact SS in 176 M_y. This creates an equatorial ridge as ancient as 4.3 G_y old. The profile of the collapsing orbit is given in Figure 7. In this scenario de-spun time is lengthened hence this scenario is rejected [55-59].

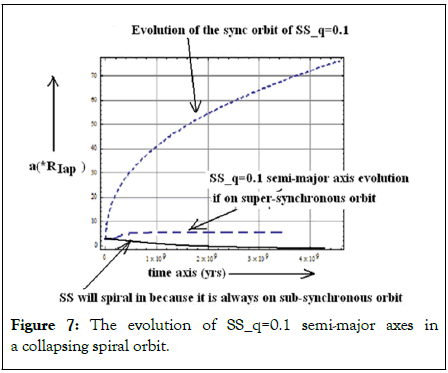
Figure 7: The evolution of SS_q=0.1 semi-major axes in a collapsing spiral orbit.

The evolutionary history of SS for q=0.04

SS for q=0.04 is the classical core-accretion process by which the sub-satellite has been formed. From Table 4, the synchronous orbit ‘a_sync (2.59 R_Iap)’>‘a_G1=2.58 R_Iap’ therefore right from the beginning SS at q=0.04 is doomed to be trapped in a death spiral and make an impact at 726.4 M_y after the debris generating impact. This SS impact will create an equatorial ridge but not an ancient one [60].

This scenario is ruled out. This gives a much larger non-hydrostatic equilibrium anomaly. It does not help in de-spinning because SS is caught in sub-synchronous orbit and the SS will spiral-in and impact Iapetus causing it to spin up and the SS impact produces a recent equatorial ridge which is as recent as 4500 M-726.4 M=3.773 G_y old.

The evolutionary history of SS for q=0.006

SS for q=0.006 has ‘a_sync=2.563 R_Iap’=‘a_G1=2.563 R_Iap’ so here SS may be placed in super-synchronous orbit. This is a suitable case for studying from de-spinning point of view (Figure 8).

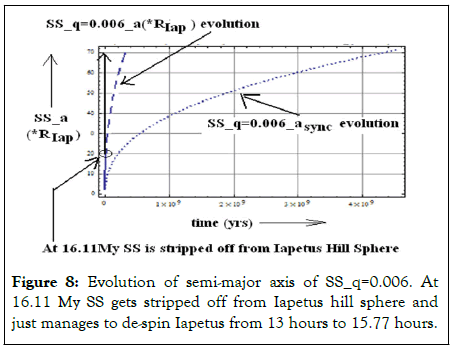
Figure 8: Evolution of semi-major axis of SS_q=0.006. At 16.11 M_y SS gets stripped off from Iapetus hill sphere and just manages to de-spin Iapetus from 13 hours to 15.77 hours.

At 16.11 M_y, SS is stripped off from Iapetus Hill Sphere. At 16.11 M_y after the debris generating impact, SS orbital period itself de-spins from 13 hours to 283 hours because it has spiraled out from an orbit of semi-major axis a_G1=1.88561 m × 10⁶ m to a_strip=14.7126 m × 10⁶ m. The ratio (ω/Ω) has a value 17.9659 at a_strip=14.7126 m × 10⁶ m therefore spin period of Iapetus at point of stripping is only 15.77 hours. There is insignificant de-spinning and according to this scenario the non-hydrostatic equilibrium anomaly should be much larger corresponding to 13 hours whereas it is corresponding to 16 hours. Therefore this scenario is completely rejected [61].

The evolutionary history of SS for q=0.0001

This is the classical core-accretion process by which the Sub-Satellite has been formed. At orbital radius of 20 R_Iap=14.7126 m × 10⁶ m, the orbital period of SS is 284.2 hours. The ratio (ω/Ω) at this radius is 17.96 therefore the spin period of Iaptus is 15.82 hours. This happens in 0.247 year. That is almost instantaneously after the impact generated disc formation Iapetus is de-spun from 13 hours to 16 hours and SS gets stripped off Iapetus . From this point onward Iapetus is de-spun by Saturn.

If there was no SS then Saturn-Iapetus System would have taken 1.68 M_y to de-spin from 13 hours to 16 hours confronting us with the problem of justifying non-hydrostatic equilibrium anomaly corresponding to 16 hours.

Discussion

In Tables 8 and 9, we give the summary of results obtained from Swift-WHM integrator and the results from primary-centric analysis respectively.

Table 8: Summary of the results obtained by Swift-WHM integrator.

Table 9: Summary of the results obtained by primary-centric analysis.

By inspection of Tables 8 and 9 we see that \citet(lev11) have a fundamental difference in their approach from that taken in this paper. \citet(lev11) start from a spin period of 16 hours whereas in this paper we start from 13 hours hence according to us a mechanism must exist which can de-spin Iapetus from 13 hours to 16 hours in a short period of several 100 years. Only then a fossil bulge of 16 hours can be explained.

So the claim of \citet (lev11), “Thus this work provides a complete story from original to final impact which may explain the ridge, shape and basin population on Iapetus” does not stand up to close scrutiny.

\citet(lev11) have not been able to justify the formation of ancient equatorial ridge in as straight forward manner as has been done in the present paper.

Also from kinematic model based analysis, Sub-satellite have no role to play in the overall reduction of de-spin time whereas \citet(lev11) have found a reduction of (× 1/10) in the de-spun time at q=0.02.

So all said and done, the two papers are at complete loggerhead with each other.

Conclusion

Kinematic Model based analysis finds q=0.4 as the best option in which Sub-satellite are able contribute in a meaningful manner in explaining the ridge, shape and basin population on Iapetus from the original to the final impact. Whereas \citet(lev11) find q=0.02 as the best SS candidate for explaining the various features of Iapetus.

Because of this strong divergence I would suggest that we repeat the whole exercise using an advanced symplectic integrator. This will verify the basic premises of kinematic model based analysis.

The theoretical analysis of this problem by kinematic model based formulation has given a new insight in the binary- formation process.

For $0.2<q<1.0$, the binary formation is by hydro-dynamic instability pathway and the time scale of formation is in years. This is standard formation process in star pairs and brown dwarf pairs. Here we have no evolutionary histories. The binary pair immediately stabilizes at outer Clarke’s configuration.

For 0.0001<q<0.2, the formation pathway is by core accretion in the primary-stellar debris disk and the time scale of formation and evolution is a strong function of ‘q’. Higher ‘q’ corresponds to shorter time scale and lower ‘q’ corresponds too much longer time-scale. Along the full range of q from 0.2 to less than 0.0001, the time scale extends from K_y to M_y to G_y to T_y. Here the tidal evolutionary history can always be analyzed.

The validity of this whole conclusion is subject to the validity of the basic premises of the kinematic model based analysis.

Acknowledgement

I acknowledge the cooperation extended by the director, IIT, Patna, in letting me use the library facilities of his central library.

Conflict of Interest

I have no conflict of interest financial or otherwise whatsoever with anybody.

References

1. Porco CC, Baker E, Barbara J, Beurle K, Brahic A, Burns JA, et al. Cassini imaging science: Initial results on Phoebe and Iapetus. science. 2005;307(5713):1237-1242.

   [Crossref] [Google Scholar] [PubMed]

2. Castillo-Rogez JC, Matson DL, Sotin C, Johnson TV, Lunine JI, Thomas PC. Iapetus' geophysics: Rotation rate, shape, and equatorial ridge. Icarus. 2007;190(1):179-202.

   [Crossref] [Google Scholar]

3. Lambeck K, Pullan S. The lunar fossil bulge hypothesis revisited. Phys Earth Planet Inter. 1980;22(1):29-35.

   [Crossref] [Google Scholar]

4. Garrick-Bethell I, Wisdom J, Zuber MT. Evidence for a past high-eccentricity lunar orbit. Science. 2006;313(5787):652-625.

   [Crossref] [Google Scholar] [PubMed]

5. Mound JE, Mitrovica JX, Forte AM. The equilibrium form of a rotating Earth with an elastic shell. Geophys J Int. 2003;152(1):237-241.

   [Crossref] [Google Scholar]

6. Zuber MT, Smith DE. Mars without tharsis. J Geophys Res. 1997;102(E12):28673-28685.

   [Crossref] [Google Scholar]

7. Dombard AJ, Cheng AF, McKinnon WB, Kay JP. The weirdest topography in the outer solar system: The ridge on Iapetus and its possible formation via giant impact. InAGU fall meeting abstracts. 2010;2010:P31D-01.

   [Google Scholar]

8. Dombard AJ, Cheng AF. Constraints on the evolution of Iapetus from simulations of its ridge and bulge. In 39^th Annual Lunar and Planetary Science Conference. 2008;1391:2262.

   [Google Scholar]

9. Kokubo E, Ida S, Makino J. Evolution of a circumterrestrial disk and formation of a single Moon. Icarus. 2000;148(2):419-436.

   [Crossref] [Google Scholar]

10. Sandwell D, Schubert G. A contraction model for the flattening and equatorial ridge of Iapetus. Icarus. 2010;210(2):817-822.

    [Crossref] [Google Scholar]

11. Caven R. Idiosyncratic Iapetus. Science News. 2007;172:104-106.
12. Sharma BK. Basic mechanics of planet-satellite interaction with special reference to Earth-Moon System. arXiv preprint arXiv:0805.0100. 2008.

    [Google Scholar]

13. Sharma BK. Theoretical formulation of the phobos, moon of mars, rate of altitudinal loss. arXiv preprint arXiv:0805.1454. 2008.

    [Google Scholar]

14. Sharma BK. Theoretical formulation of the origin of cataclysmic late heavy bombardment era based on the new perspective of birth and evolution of solar systems. arXiv preprint arXiv:0807.5093. 2008.

    [Google Scholar]

15. Sharma BK, Ishwar B, Rangesh N. Simulation software for the spiral trajectory of our Moon. Adv Space Res. 2009;43(3):460-466.

    [Crossref] [Google Scholar]

16. Canup RM, Ward WR. A common mass scaling for satellite systems of gaseous planets. Nature. 2006;441(7095):834-839.

    [Crossref] [Google Scholar]

17. Mayer L, Quinn T, Wadsley J, Stadel J. Formation of giant planets by fragmentation of protoplanetary disks. Science. 2002;298(5599):1756-1759.

    [Crossref] [Google Scholar] [PubMed]

18. Sharma BK. The architectural design rules of solar systems based on the new perspective. Earth, Moon, and Planets. 2011;108:15-37.

    [Crossref] [Google Scholar]

19. Krasinsky GA. Dynamical history of the Earth-Moon system. Celest Mech Dyn. 2002;84:27-55.

    [Crossref] [Google Scholar]

20. Carlberg JK, Majewski SR, Arras P. The role of planet accretion in creating the next generation of red giant rapid rotators. Astrophys J Lett. 2009;700(1):832.

    [Google Scholar]

21. Jackson B, Barnes R, Greenberg R. Observational evidence for tidal destruction of exoplanets. Astrophys J Lett. 2009;698(2):1357.

    [Google Scholar]

22. Jackson B, Greenberg R, Barnes R. Tidal heating of extrasolar planets. Astrophys J. 2008;681(2):1631.

    [Google Scholar]

23. Hellier C, Anderson DR, Cameron AC. An orbital period of 30.94d for hot-Jupiter Planet WASP18b. Nature. 2009;460:1098-1100.
24. Israelin G, Santos NC, Meyer M, Rebala R. Evidence of planet engulfment of the star HD 82943. Nature. 2001;411:163-166.
25. Bloom JS, Giannios D, Metzger BD, Cenko SB, Perley DA, Butler NR, et al. A possible relativistic jetted outburst from a massive black hole fed by a tidally disrupted star. Science. 2011;333(6039):203-206.

    [Crossref] [Google Scholar] [PubMed]

26. Jeans SJ. How the moon will disintegrate. Nenones’ Practical Machines. 1936.
27. Santos NC, Benz W, Mayor M. Extrasolar planets: Constraints for planet formation models. Science. 2005;310(5746):251-255.

    [Crossref] [Google Scholar] [PubMed]

28. Hamilton DP, Burns JA. Orbital stability zones about asteroids: II. The destabilizing effects of eccentric orbits and of solar radiation. Icarus. 1992;96(1):43-64.

    [Crossref] [Google Scholar]

29. Alley CO, Bender PL, Dicke RH, Faller JE, Franken PA, Plotkin HH, et al. optical radar using a corner reflector on the moon. J Geophys Res. 1965;70(9):2267-2269.

    [Crossref] [Google Scholar]

30. Astakhov SA, Burbanks AD, Wiggins S, Farrelly D. Chaos-assisted capture of irregular moons. Nature. 2003;423(6937):264-267.

    [Crossref] [Google Scholar]

31. Chandrashekher S. Ellipsoidal figures of equilibrium. The Saliman Foundation Lectures, Yale University Press, New Horizon. 1969.
32. Cook CL. Comment on ‘Gravitational Slingshot’, by Dukla JJ, Cacioppo R and Gangopadhyaya. A. Am J Phys. 2004;72(5):619-621.
33. Czechowski L, Leliwa-Kopystynski J. The Iapetus’s ridge: Possible explanations of its origin. Adv Space Res. 2008;42(1):61-69.

    [Crossref] [Google Scholar]

34. Darwin GH. XIII. On the precession of a viscous spheroid, and on the remote history of the Earth. Philos Trans R Soc. 1879;31(170):447-538.

    [Crossref] [Google Scholar]

35. Darwin GH. On the secular changes in the elements of the orbit of a satellite revolving about a planet distorted by tides. Nature. 1880;21(532):235-237.

    [Crossref] [Google Scholar]

36. Dickey JO, Bender PL, Faller JE, Newhall XX, Ricklefs RL, Ries JG, et al. Lunar laser ranging: A continuing legacy of the Apollo program. Science. 1994;265(5171):482-490.

    [Crossref] [Google Scholar] [PubMed]

37. Dollinger MP, Hatzes AP, Pasquini L, Guenther EW, Hartmann M, Girardi L, Esposito M. Discovery of a planet around the K giant star 4 Ursae Majoris. Astronomy and Astrophysics. 2007;472(2):649-652.

    [Google Scholar]

38. Dollinger MP, Hatzes AP, Pasquini L, Guenther EW, Hartmann M. Planetary companions around the K giant stars 11 UMi and HD 32518. arXiv preprint arXiv:0908.1753. 2009.

    [Google Scholar]

39. Dykla JJ, Cacioppo R, Gangopadhyaya A. Gravitational slingshot. Am J Phys. 2004;72(5):619-621.

    [Google Scholar]

40. Epstein KJ. Shortcut to the slingshot effect. Am J Phys. 2005;73(4):362.

    [Crossref] [Google Scholar]

41. Faller J, Winer I, Carrion W, Johnson TS, Spadin P, Robinson L, et al. Laser beam directed at the lunar retro-reflector array: Observations of the first returns. Science. 1969;166(3901):99-102.

    [Crossref] [Google Scholar] [PubMed]

42. Giese B, Denk T, Neukum G, Roatsch T, Helfenstein P, Thomas PC, et al. The topography of Iapetus' leading side. Icarus. 2008;193(2):359-371.

    [Crossref] [Google Scholar]

43. Han I, Lee BC, Kim KM, Mkrtichian DE, Hatzes AP, Valyavin G. Detection of a planetary companion around the giant star γ1 Leonis. Astrophys. 2010;509:A24.

    [Google Scholar]

44. Ida S, Canup RM, Stewart GR. Lunar accretion from an impact-generated disk. Nature. 1997;389(6649):353-357.

    [Crossref] [Google Scholar]

45. Ip WH. On a ring origin of the equatorial ridge of Iapetus. Geophys Res Lett. 2006;33(16).

    [Crossref] [Google Scholar]

46. Jones JB. How does the slingshot effect work to change the orbit of a spacecraft? Scientific American. 2005;293(5):116.

    [Google Scholar]

47. Kemble EC. Physical science, its structure and development: From geometric astronomy to the mechanical theory of heat. 1996.

    [Google Scholar]

48. Mayor M, Bonfils X, Forveille T, Delfosse X, Udry S, Bertaux JL, et al. The HARPS search for southern extra-solar planets XVIII. An Earth-mass planet in the GJ 581 planetary system. arXiv preprint arXiv:0906.2780. 2009.

    [Google Scholar]

49. Matsuyama I, Mitrovica JX, Manga M, Perron JT, Richards MA. Rotational stability of dynamic planets with elastic lithospheres. J Geophys Res. 2006;111(E2).

    [Crossref] [Google Scholar]

50. Melosh HJ. Global tectonics of a despun planet. Icarus. 1977;31(2):221-243.

    [Crossref] [Google Scholar]

51. Murray CD, Dermott SF. Solar system dynamics. Cambridge University Press; 1999.

    [Google Scholar]

52. Nesvorny D, Alvarellos JL, Dones L, Levison HF. Orbital and collisional evolution of the irregular satellites. Astron J. 2003;126(1):398.

    [Google Scholar]

53. Niedzieiski A, Novoski G, Adamow M, Wolszczan A. Substeller-mass companions to the K-dwarf BD+14 4559 and the K-giants HD 240210 and BD+20 2457. Ap J. 2009;707(1):768-777.

    [Crossref]

54. Niedzielski A, Konacki M, Wolszczan A, Nowak G, Maciejewski G, Gelino CR, et al. A planetary-mass companion to the K0 giant HD 17092. Ap J. 2007;669(2):1354.

    [Google Scholar]

55. Roatsch T, Jaumann R, Stephan K, Thomas PC. Cartographic mapping of the icy satellites using ISS and VIMS data. Saturn from cassini-huygens. 2009:763-781.

    [Crossref] [Google Scholar]

56. Roberts JH, Nimmo F. Tidal dissipation due to despinning and the equatorial ridge on Iapetus. In 40^th Annual Lunar and Planetary Science Conference 2009;40:1927.

    [Google Scholar]

57. Robuchon G, Choblet G, Tobie G, Cadek O, Sotin C, Grasset O. Coupling of thermal evolution and despinning of early Iapetus. Icarus. 2010;207(2):959-971.

    [Crossref] [Google Scholar]

58. Sato BE, Toyota E, Omiya M, Izumiura H, Kambe E, Masuda S, et al. Planetary companions to evolved intermediate-mass stars: 14 Andromedae, 81 Ceti, 6 Lyncis, and HD167042. Publ Astron Soc Jpn. 2008;60(6):1317-1326.

    [Crossref] [Google Scholar]

59. Thomas PC. Sizes, shapes, and derived properties of the saturnian satellites after the Cassini nominal mission. Icarus. 2010;208(1):395-401.

    [Crossref] [Google Scholar]

60. Udry S, Bonfils X, Delfosse X, Forveille T, Mayor M, Perrier C, et al. The HARPS search for southern extra-solar planets XI. Super-Earths (5 and 8 M_Earth) in a 3-planet system. arXiv preprint arXiv:0704.3841. 2007.

    [Google Scholar]

61. Zoghbi JP. Quantization of planetary systems and its dependency on stellar rotation. Publ Astron Soc Aust 2011;28(3):177-201.

    [Google Scholar]