Journal of Biomedical Engineering and Medical Devices
Open Access
ISSN: 2475-7586
ISSN: 2475-7586
Research Article - (2016) Volume 1, Issue 3
Keywords: Single-step saccades; Double-step saccades; Duration; Latency; Clustering
Voluntary saccades are often made in response to sensory inputs, namely visual, auditory, and auditory-visual bisensory stimuli. Visually elicited saccades have been investigated extensively, including the oculomotor plant and the neural signals that drive the eye movements [1-10]. As we hear a running spectral content of sounds in ambient air, much remains for the brain to sift through that content and extract the location and meaning of sounds. Certain sounds cause saccadic eye movements. Saccade responses to auditory and auditory-visual stimuli have been presented in the literature that primarily focused on auditory saccade accuracy and latency [11-24]. Some have reported that the latent period of auditory saccades decreases with increasing target eccentricity [11-15] or at least is greater in small saccades than in larger saccades [16]. By comparing saccades that are triggered by different types of stimuli, a significant reduction of latent period is found in auditory-visual bisensory saccades [17,20,21]. It has also been shown that auditory saccades have lower peak velocity, longer duration and are less accurate than visual saccades [16,19,23]. When presenting two sequential sound tones to humans, an interesting saccadic response emerges: the neural inputs to the oculomotor plant determine whether the response contains two sequential saccades or only one. This intrinsic neural mechanism governs the degree of nonlinearity of stimulus-to-response transformation. The response including sequential saccades here is referred to as double-step, whereas the single-step response comprises only one saccade. It is our goal to identify the type of generated saccade in auditory double-step trials. The mechanism that brings into terms the differences in saccade characteristics to visual, auditory, and auditory-visual bisensory stimuli is lately examined [22-24]. The noticeable number of saccades therein provides a unique groundwork for the analysis and inference thereof. This growing dataset of saccades enables more insights into dynamical control involved in the oculomotor plant and neuromuscular systems. Further, the time-optimal neuronal control strategy delineated there [25,26] to estimate the agonist/antagonist active-state tensions is proven sufficient in other saccade paradigms and tested out for different oculomotor plant models and muscle fiber models. The new double-step paradigm shows that the time-optimality is still applicable to saccadic responses to successive targets. In progression, a linear quadratic tracking algorithm is debuted to smoothly pursue a target given the physiological limitations of neural transmission delays [27,28]. Here we consider experiments in which two successive auditory stimuli in a staircase pattern are presented, in response to which the human subjects make a sequence of saccadic eye movements; that is, only one saccade (single-step) or two saccades (double-step). To appreciate the differences in saccade dynamics, it is often helpful to describe them with saccade main-sequence diagrams [3-10,22-24]. These diagrams mandate estimation of the parameters, including peak velocity, duration, latency, and the neural input of agonist pulse, using a system identification technique [5,6]. The duration of a saccade is the time from the start to the end of a saccade, and the latency is the time from the onset of stimulus to the onset of a saccade (Figure 1). In this study we hypothesize that extracting the duration and latency of each saccade proves useful in finding the type of the generated saccade. Therefore, we propose a framework to estimate the duration and latency from the data. We first derive the acceleration from the position data and apply an adaptive threshold algorithm, which gives an initial number of saccades and their durations. We then check these saccades against the constraints on the minimum values of duration of each saccade and inter-saccade interval. The post saccade overshoot, if any, is suppressed next. The estimated duration for each saccade is then analyzed to find its corresponding latency. Finally, the sum of latency values is used to identify the saccade type via an inferential clustering technique. This framework is applicable to large datasets which contain scores or even hundreds of saccades position data for inferential analysis.
Figure 1: Schematic representation of the sequence of target events (a), and saccadic responses: (b) double-step and (c) single-step. A is saccade amplitude, L is latency, and Dur is saccade duration. S is target duration. D is delay is defined as the time between the end of first peripheral target presentation and the onset of initial saccade (L1-S1). Int is the inter-saccade interval in response.
Subjects
Four subjects, two males and two females, aged 20-26, participated in this study. None of the subjects disclosed any history of visual, auditory or vestibular disorders, and none were taking any medications known for central nervous system illnesses. One male and one female had dark colored eyes while the other two had light colored eyes. All subjects demonstrated normal visual and auditory functions.
Apparatus and experiment design
All the tests were performed in an independent, quiet room with normal illumination. Subjects were seated with head stabilized by a high speed eye tracking device (1250 Hz sample rate, by SensoMotoric Instruments (SMI)). The auditory targets were tone signals at 1 kHz frequency with an average intensity around 60 dB SPL. 3D positional audio was implemented using H3D Binaural Spatializer plug-in (by Longcat Audio Technologies) inserted in audio editing software (Adobe Audition CS5.5), and the sounds were heard by a stereo noise-reduced headphone. Targets were presented at angles of 0°, 5°, 10°, 15° and 20° from the center to left or right in the horizontal plane which was 830 mm in front of the subjects. To facilitate the performance, a visual cue (white solid dots of 4 mm diameter on a grey background) was displayed on a monitor when the auditory target was at the center. The peripheral auditory stimuli were presented alone without visual cues. The experiments were computer-controlled using custom written software while data were collected using the eye tracker implemented in the iView X™ system by SMI. The subjects were instructed to locate the position of the auditory target by moving their eyes as fast as possible. There were two test sessions with the first peripheral target’s duration (S1, shown in Figure 1a) set as 140 and 210 ms. In the double-step paradigm, the target stepped up twice laterally in the horizontal. Particularly, each session included multiple trials, based on 0°-5°-10° or 0°-10°-20° double-step displacements to right or left. We kept the 0.5 second worth of data after the onset of the first peripheral stimulus (step). The recorded saccade data contained either double-step (Figure 1b) or single-step (Figure 1c) responses. There were four different datasets, together including 298 saccades, with results listed in Table 1. The illustrations in this paper are those of the analysis of the first dataset.
| Dataset | A1(°) | A2(°) | S1(s) | S2(s) |
|---|---|---|---|---|
| 1 | 5 | 10 | 0.14 | 0.36 |
| 2 | 5 | 10 | 0.21 | 0.29 |
| 3 | 10 | 20 | 0.14 | 0.36 |
| 4 | 10 | 20 | 0.21 | 0.29 |
Table 1: Stimulus parameters for four datasets in this study.
Data analysis method
Raw data contained pupil and gaze information were generated automatically by the iView X™ system. Gaze data from the left eye were recorded in pixels, and then converted to degrees. The first dataset stacked the eye position data in degrees for 64 saccades. Each saccade may be of nature of either single-step or double-step that depended on the subject’s response. Velocity and acceleration are two important components in the study of the ocular motor system. The raw saccade velocity was calculated using the twopoint central difference method. A low-pass filter of zero-phase shifting was then applied to the raw velocity. The cutoff frequency was selected 74 Hz as the maximum frequency of saccade velocity. Similarly, saccade acceleration was calculated by applying the twopoint central difference method to the filtered velocity data. Figure 2 shows these processes for a sample double-step saccade (dashed line in Figure 2a). The core part of the data analysis was to develop a saccade detection algorithm. This part matters to distinguish singlestep response from the double-step, and calculate the duration and latency of each saccade. Our method centered on saccade detection in the acceleration domain while meeting constraints in time for feasible saccades. The structure of the saccade detection algorithm is shown in Figure 3. The rationale of the flowchart was based on two factors: (1) consistency of the approach with the physiological properties of saccades, and (2) efficiency in the required memory and computational expenses involved. Algorithms used for the detection of eye movements have evolved from using a preset threshold in the velocity or acceleration domains to adaptive algorithms where the thresholds are estimated and updated across the signals [29-37]. The major effort has been to mitigate the deterring effects of recording noise, erratic gaze drifts, and stimulation artifacts on the detection and tracking performance. For detecting saccadic events, we applied an adaptive threshold method, Niblack’s algorithm [38], in the acceleration signal a(t). This algorithm calculated a local threshold, Thr, by shifting a rectangular window W across the signal to calculate the local mean and local variance Var of the signal. The threshold was determined as
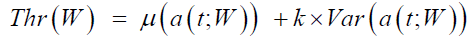 (1)
(1)
Figure 3: Flowchart of the algorithm for saccade detection and estimating its duration. An index vector was calculated from the acceleration data and was tested against conditions on duration of each saccade and inter-saccade interval. Saccadic intervals are bounding boxes including data for each type of saccade (number of intervals is either one (single-step) or two (double-step)).
where=-10-4. The window included 100 samples (80 ms in extent). This choice was made because for saccades under 20 degrees, saccade duration was less than 80 ms.
hen, a rectangular index vector function I(t) representing the approximate saccadic intervals was defined as
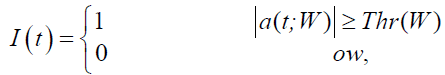 (2)
(2)
where ones indicated detected saccades and zeros reflected fixations of eye movements. An approximate saccadic interval must have duration larger than T=6 ms to be valid. This constraint was to omit some artifacts at the beginning and the end of the data. At the same time, since two saccades could not appear closer than a certain time, tmin, which is the time corresponding to the minimum duration of the inter-saccade interval, two detected saccades that occur closer than tmin were merged. Here tmin was chosen 25 ms. Lastly, since we had either double-step or single-step saccades, one or two intervals should be detected. However, if the number of intervals was more than two, post saccade overshoot might be included, and the overshoot was suppressed before the duration calculation. This calculation was done by finding the time points of rising and falling edges in the index vector, and duration was the time difference between the two edges. After calculating duration for each detected saccade, we sought to find its respective latency by searching in the velocity domain for the saccadic onset. To do so, we traced back the signal from the rising edge of each saccadic interval to the sample where the velocity was nearing zero o/s and increasing after that. The latency was then defined as the difference between the saccadic onset and the onset of its related stimulus. There had to be two latency values for double-step response or only one for single-step response. It appealed intuitively that the sum of latency then was higher for the double-step than single-step, with some marginal overlap. We thus assumed that the sum of latency was the best descriptor to discriminate between the two responses. We labeled the saccades based on this sum so that saccades which had only one latency were identified as single-step, whereas those with two latency values were deemed double-step. We denote this labeling an inferential clustering technique. There were cases in which the sum of latency values was unacceptably low (below 1 ms). In those cases such latency values, and their base saccades, were construed as missed cases (false-negatives). We excluded those cases from the dataset and then run the k-means clustering on the dataset. Figure 4 sketches the flowchart of the algorithm of this fold of the work.
Figure 5 demonstrates the saccade detection for four different responses in the first dataset. The rectangular index vector function locates the saccades reliably. The saccadic intervals are shown for a single-step case as well as two double-step cases. There is one double-step case for which the algorithm does not detect the intervals correctly. This miss might be due to the effects of stimulation artifacts at the beginning of the recording. After saccade detection and latency calculation, the clustering techniques yielded the saccade type. Figure 6 shows the clustering results. Top row shows the scatter plot of sum of latency values obtained for all detected saccades. The middle inset exhibits the results of inferential clustering that provides whether a response is a single-step or a double-step saccade. K-means clustering was also used to allow for comparison of the performance. The clustering result appears at the bottom of Figure 6. It appears that k-means labels more of the double-step data as single-step (see, e.g., saccade #30 misidentified in Figure 6c as single-step. This is the case since k-means clusters the sum values into two groups in order to minimize the within-cluster norm-2 distance. It thus follows that the inferential clustering outperforms k-means. We assessed the performance of the algorithms for all the datasets in this study. Table 2 shows the numbers of total saccades, NT, of detected single-step saccades, NSing, of detected double-step saccades, NDoub, and of missed cases, NMiss, resulted from the inferential clustering. The percentage probability of double-step occurrence is also included as PDoub, as well as the detection probability of the algorithms shown by PD. This probability is defined as the complement of probability of miss.
Figure 5: Clustering results for the 64 saccades in the first dataset. The sum of latency values is shown in (a). The inferential clustering yielded 37 double-step cases, 22 single-step cases, and 5 missed cases in (b). K-means clustering turned few double-step cases into single-step cases in (c). Note that missed cases are not included in data for k-means clustering.
| Dataset | NT | NSing | NDoub | NMiss | PDoub (%) | PD (%) |
|---|---|---|---|---|---|---|
| 1 | 64 | 22 | 36 | 6 | 56.3 | 90.6 |
| 2 | 85 | 23 | 58 | 4 | 68.2 | 95.3 |
| 3 | 59 | 8 | 49 | 2 | 83.1 | 96.6 |
| 4 | 90 | 12 | 71 | 7 | 78.9 | 92.2 |
Table 2: Number of detected single- or double-step saccades and the detection probability for the datasets.
Probability of double-step occurrence
Characteristics of goal-oriented saccades elicited by visual, auditory-visual and auditory targets are delineated [5,6,18,22-24,39,40]. Saccade response patterns are related to time delay D, which is the time between the end of the first target presentation and the onset of the initial saccade (Figure 1). It is shown that single-step responses occur with long delays, while double-step responses arise with short delays. Here with auditory stimuli, we found that 0°-10°-20° doublestep trials (the third and fourth datasets) showed relatively higher percentage of PDoub than their respective counterparts in 0°-5°-10° (the first and second datasets). The detection probability in the third dataset turned out to be the highest one. Double-step saccades show a similar programming mechanism with visual or auditory input; that is, when a second target is applied, the programming of the preceding saccade ends and the programming of the saccade to the new target starts at once. As the inter-stimulus interval increases, the preceding saccade programming cannot be modified [41-44]. The algorithm of saccade detection here worked well for responses to different types of double-step stimuli. It was robust against the stimulation artifacts at the beginning and end of the recording, and suppressed the post saccade overshoot in response to the second step of the stimulus. For evaluating the detection performance, any reliable inference mandates sufficient number of observations from one phenomenon in repeated experiments. The inferential clustering relied on this fact and revealed the type of the response from adequate number of intermingled singleand double-step responses. The distinction metric of this clustering was the sum of latency values of the response, since it was higher in doublestep case than in single-step case.
Parallel programming
Previous studies have suggested the parallel programming indicating that programming of a second saccade can be initiated prior to the execution of a preceding saccade [22-24,41,42,45,46]. If the two saccades are programmed in parallel, each step is only responsible to one of the two targets, and the second step should occur in a relatively fixed period after the onset of the second target, regardless of the timing of the initial saccade [7]. Third, the parallel programming of the two saccades is shown to occur mostly when the delay is less than 50 ms [23]. However, when there is a short inter-saccade interval (close to simultaneous case), there may be a penalty such that the latency of the second-step saccade increases. Note that in visual double-step saccades, the mean latency of the second saccade, L2, is generally longer than that of the first saccade, L1. This indicates a reduction in the speed of processing the second saccades [23]. Shown in Figure 6 are the distributions of L1 and L2 for auditory double-step saccades detected here. For the case of 0°-5°-10° double-step stimulus, it appears that in some regions (e.g., toward the end of the latency range) L2 is longer than L1. For the other case of 0˚-10˚-20˚, the distributions of L1 and L2 are overlapped and close to each other, so there is not a vivid remark about the dominance of the range of one versus the other.
This work focused on identifying double-step saccades from auditory double-step stimuli presented to human subjects. For this purpose, we first detected saccades from the streams of recorded data. The detected saccades were then analyzed in order to estimate their durations and latency values. For the double-step responses there were two putative steps, where in single-step responses only one step was observed. Finally, the sum of latency values was calculated as the basis of an inferential clustering algorithm to identify the type of saccades. The accuracy of the double-step responses was higher for the doublestep stimuli with higher amplitudes of the two steps in each double-step stimulus. We believe that the analysis of double-step saccades leads to a finer understanding of the neural control of goal-oriented saccades. The algorithms in this work can be generalized to be tested in other datasets that may include various types of saccades.