Journal of Medical Diagnostic Methods
Open Access
ISSN: 2168-9784
ISSN: 2168-9784
Research Article - (2015) Volume 4, Issue 4
The Cancer Genome Atlas (TCGA) project has made available multiple heterogeneous datasets. Although several methodological approaches have been proposed for the heterogeneous data integration, there is no framework of sparse non-negative matrix factorization (NMF) for handling heterogeneous biological data integration. Here, we propose the block-weighted sparse NMF bwsNMF) to identify tumor subtypes of endometrial carcinoma by integrating gene expression, mutations, a protein-protein interaction network and a transcription factor target network.
Keywords: Cancer subtype; Personalized medicine; Weighted sparse NMF
Clustering algorithms have been applied to the identification of new subtypes of human cancer. Clustering of heterogeneous datasets represents a difficult clustering problem to which some clustering methods cannot be easily extended. Clustering methods based on matrix computations, such as non-negative matrix factorization (NMF), can be modified to deal with this complex problem. In this paper, we will show how the formulation of NMF can be modified for tumor subtype identification with multiple heterogeneous datasets.
An important question concerns the application of different weights to the multiple heterogeneous datasets. A gold standard reference is needed to choose the weight parameters. In supervised classification problems or semi-supervised clustering problems, we have a training set that can be used for parameter-tuning with cross-validation. However, our objective is to determine weight parameters when there is no training set that has subtype labels. We use another type of data, i.e. clinical data including survival days of patients, to determine weight parameters after defining the best subtypes consisting of patient groups that show different survival profiles. In other words, our objective is to identify tumor subtypes that maximize survival differences by searching the weight parameter space. We believe that NMF provides a useful mathematical framework to formulate a more complex objective function without losing computational efficiency.
The current general approach to personalized cancer genomic medicine is based on the identification of cancer subtypes from genomic profiles. The most widely used genomic profile is derived from gene expression data. Because some cancer types are driven by somatic mutations or copy number aberrations, it is logical to use multiple heterogeneous datasets to identify more meaningful cancer subtypes with clinical relevance.
Tumor subtyping is a classic clustering problem that is one of the major focus areas in computer science and statistics. Although there are many clustering algorithms being developed, it is difficult to assess which algorithm is the best performer, because they tend to be situationspecific, and the performance of each algorithm generally depends on the dataset. Nevertheless, there is a strong rationale to choose an algorithm that generally performs well to identify clusters in a given
dataset and allows for easier interpretation, improving our ability to understand the given data and identify new biological knowledge. This is one of the reasons why many computational biologists have used hierarchical clustering (HC) with various distance metrics. One of common sub-problems with this approach is how we can determine the number of clusters. In order to identify the number of clusters and membership stability, consensus HC was developed [1] in 2003. Some authors who developed the consensus HC later participated in applying an NMF algorithm [2] to bioinformatics and computational biology to discover metagenes and molecular patterns [3]. However, the NMF algorithm based on multiplicative update rules (i.e. gradient descent method) can suffer from convergence issue [4]. Therefore, some NMF algorithms [5,6] based on Newton’s method have been developed and applied to bioinformatics and computational biology [7]. These NMF algorithms based on alternating least squares usually showed faster convergence speed, so they have been implemented by multiple computer languages (e.g., NMF Matlab toolbox [8] in Matlab, NIMFA in Python [9]). Recently, subtypes of adult de novo acute myeloid leukemia have been identified by NMF instead of HC [10].
The Cancer Genome Atlas (TCGA) project has generated multitype genomic datasets as well as clinical data. Tumor subtyping has been primarily done with gene expression profiles, because gene expression is considered to be the output of all regulatory variations/ profiles such as SNPs, mutations, structural variations (SVs), copy number variations (CNVs), microRNA profiles and DNA methylation profiles. The TCGA community has proposed four subtypes (classical, neural, mesenchymal and proneural) in glioblastoma [11] with gene expression profiles and four main breast cancer subtypes (cluster1: similar to PAM50 HER2-enriched, cluster2: PAM50 Basal, cluster3:
PAM50 Luminal A, and cluster4: PAM50 Luminal B) when combining five heterogeneous datasets (miRNA, DNA methylation, copy number, gene expression and reverse-phase protein array (RPPA) dataset) [12] with consensus HC. mRNA expression profiles of colorectal cancer were clustered into three distinct clusters [13,14], but they were not associated with any clinical phenotype such as patient survival or response to chemotherapy [15]. mRNA expression profiles of lung squamous cell carcinoma (SQCC) were categorized into four subtypes (classical, basal, secretory and primitive) [16] with the previously reported lung SQCC gene expression-subtype signatures.
In this paper, we propose the block-weighted sparse NMF (bwsNMF) to identify subtypes of endometrial carcinoma by integrating gene expression data, gene mutations, a protein-protein interaction network, and a transcription factor target network.
Sparse NMF
We briefly review a type of sparse NMF (sNMF) based on alternating non-negativity-constrained least squares6 to impose sparseness constrained on basis/metagene matrix:
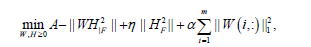 (1)
(1)
where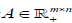 nis the non-negative input (m genes n patients) matrix,
nis the non-negative input (m genes n patients) matrix, 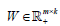 is the basis/metagene matrix,
is the basis/metagene matrix,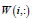 is the coefficient/loading matrix, W (i,:) is the ith row vector of W, η>0 is a parameter to suppress
is the coefficient/loading matrix, W (i,:) is the ith row vector of W, η>0 is a parameter to suppress 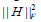 and
and 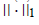 is a regularization parameter to balance the trade-off between accuracy of approximation the sparseness of W6. Because this formulation has the L1- norm (i.e. 1 || .|| ) term, it is theoretically appropriate to introduce sparseness (exact zero values in ). Moreover, the formulation can be optimized by least squares methods due to non-negativity-constraints, which results in high convergence speed with sound convergence property. The L1-norm term can be considered without using linear programming. This particular type of sNMF is different from Lasso (a shrinkage and selection method for linear regression) is a regularization parameter to balance the trade-off between accuracy of approximation the sparseness of W6. Because this formulation has the L1- norm (i.e. 1 || .|| ) term, it is theoretically appropriate to introduce sparseness (exact zero values in ). Moreover, the formulation can be optimized by least squares methods due to non-negativity-constraints, which results in high convergence speed with sound convergence property. The L1-norm term can be considered without using linear programming. This particular type of sNMF is different from Lasso (a shrinkage and selection method for linear regression) [17], because Lasso has no square in the L1-norm term. Although sNMF [6] for sparser
is a regularization parameter to balance the trade-off between accuracy of approximation the sparseness of W6. Because this formulation has the L1- norm (i.e. 1 || .|| ) term, it is theoretically appropriate to introduce sparseness (exact zero values in ). Moreover, the formulation can be optimized by least squares methods due to non-negativity-constraints, which results in high convergence speed with sound convergence property. The L1-norm term can be considered without using linear programming. This particular type of sNMF is different from Lasso (a shrinkage and selection method for linear regression) is a regularization parameter to balance the trade-off between accuracy of approximation the sparseness of W6. Because this formulation has the L1- norm (i.e. 1 || .|| ) term, it is theoretically appropriate to introduce sparseness (exact zero values in ). Moreover, the formulation can be optimized by least squares methods due to non-negativity-constraints, which results in high convergence speed with sound convergence property. The L1-norm term can be considered without using linear programming. This particular type of sNMF is different from Lasso (a shrinkage and selection method for linear regression) [17], because Lasso has no square in the L1-norm term. Although sNMF [6] for sparser 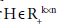 has been applied to clustering problems, sNMF for sparser
has been applied to clustering problems, sNMF for sparser 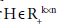 has not been applied to a clustering problem yet.
has not been applied to a clustering problem yet.
We can expand the term of
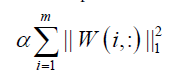
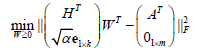
where wij≥0 is the ith row and the jth column of W≥0, k is the number of basis vectors, i.e. the number of clusters, thus, the objective function can be optimized by alternating non-negativity-constrained least squares:
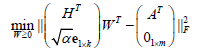 (2)
(2)
Where 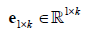 is an all-ones-vector and
is an all-ones-vector and 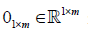 is a zero vector, and
is a zero vector, and 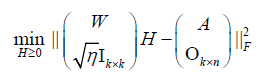 (3)
(3)
Where 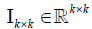 is an identity matrix and
is an identity matrix and 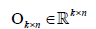 is a zero matrix [6]. This proposed algorithm is a two-block block coordinate descent (BCD) method, which satisfies Bertsekas conditions [18] for convergence (i.e. each sub-problem has a unique solution). By imposing sparseness on the basis/metagene matrix, contribution of some genes to each basis vector can be converted to zero, which may give us simpler basis vectors that consist of more important genes/features to describe the original input matrix.
is a zero matrix [6]. This proposed algorithm is a two-block block coordinate descent (BCD) method, which satisfies Bertsekas conditions [18] for convergence (i.e. each sub-problem has a unique solution). By imposing sparseness on the basis/metagene matrix, contribution of some genes to each basis vector can be converted to zero, which may give us simpler basis vectors that consist of more important genes/features to describe the original input matrix.
Here, we introduce a novel NMF called the block-weighted sparse NMF (bwsNMF) that can consider the relative importance of feature blocks as well as sparseness. When we know a set of features may have a higher or lower priority than other sets, we can divide 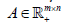 into multiple row blocks:
into multiple row blocks: 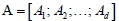 where1≤ l ≤ d is the th block matrix ( genes n patients, 1≤ l ≤ d where is the total number blocks) of
where1≤ l ≤ d is the th block matrix ( genes n patients, 1≤ l ≤ d where is the total number blocks) of 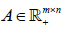 Then, the objective function of bwsNMF follows:
Then, the objective function of bwsNMF follows:
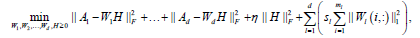 (4)
(4)
Where 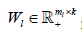 is the L th block matrix of the basis/metagene matrix
is the L th block matrix of the basis/metagene matrix 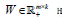 is the coefficient/loading matrix
is the coefficient/loading matrix 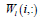 is the ith row vector of
is the ith row vector of 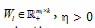 is a parameter to suppress
is a parameter to suppress 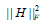 and s l > 0 is a regularization parameter to introduce zeros into
and s l > 0 is a regularization parameter to introduce zeros into 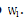 . We can still optimize the objective function with alternating non-negativityconstrained least squares:
. We can still optimize the objective function with alternating non-negativityconstrained least squares:
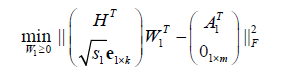 . (5)
. (5)
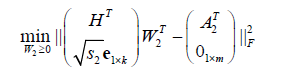 (6)
(6)
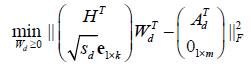 (7)
(7)
Where 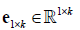 is an all-ones-vector,
is an all-ones-vector,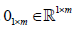 is a zero vector. The next alternating step is
is a zero vector. The next alternating step is
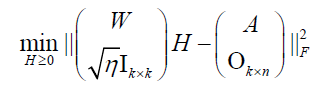 (8)
(8)
where 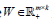 is the merged matrix from
is the merged matrix from 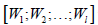 with preserved order,
with preserved order, 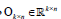 is an identity matrix, and
is an identity matrix, and 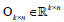 n k n is a zero matrix. The convergence criteria of sNMF can be naturally applied to this algorithm, and the fast convergence property is also preserved. This bwsNMF can incorporate biological knowledge with the weight values (s1,s2,…….sl) Larger sl gives higher chance to introduce zeros to
n k n is a zero matrix. The convergence criteria of sNMF can be naturally applied to this algorithm, and the fast convergence property is also preserved. This bwsNMF can incorporate biological knowledge with the weight values (s1,s2,…….sl) Larger sl gives higher chance to introduce zeros to 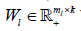 with a set of specific features for the th block.
with a set of specific features for the th block.
When we know the relative importance of feature blocks, we can reduce the searching space of the weight parameters. When we have a biological hypothesis that one feature type is more important than the other feature type for separating a clinical phenotype, we can set higher priority to the more important feature type, obtain tumor subtypes, and measure the degree of associations between subtypes and clinical phenotypes so that we can assess the quality of the biological hypothesis. When we do not have any a priori knowledge and assumptions regarding the relative importance of a feature type, we search for a set of parameters that can generate maximum separation of a clinical phenotype (e.g., survival) of patients in different groups.
Tumor subtypes have been determined by consensus HC1 or consensus NMF3, where the corresponding clustering algorithms were applied to genes usually selected by removing genes with small variances and/or removing gene profiles with low absolute expression values. Thus, the typical number of genes in the input matrix 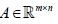 is less than 10,000 genes (i.e. m<10,000), which is a relatively small number compared to the number of total genes in the human genome. This gene selection step can be considered as a statistical treatment rather than the usage of biological knowledge.
is less than 10,000 genes (i.e. m<10,000), which is a relatively small number compared to the number of total genes in the human genome. This gene selection step can be considered as a statistical treatment rather than the usage of biological knowledge.
As an example to show bwsNMF can incorporate multitype biological knowledge, we tried to identify tumor subtypes of endometrial carcinoma with the following features: 1) somatic mutations, 2) neighbor genes of the somatic mutations, and 3) target genes of transcription factors directly or indirectly connected with somatic mutations in the cancer pathways (called as TF-target genes). Then, the typical number of genes in the input matrix 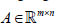 was reduced to fewer than 1000 genes (i.e. m<1,000)). High quality biological databases can be used for this initial feature selection step. However, a particular challenge is predicting the relative importance of multi-type features. Therefore, bwsNMF was repeatedly executed with a set of weight parameters inside the parameter searching space (10-8, 10-6…,1) for each sl, to find the best set of parameters that can identify tumor subtypes for which patient survival was maximally different.
was reduced to fewer than 1000 genes (i.e. m<1,000)). High quality biological databases can be used for this initial feature selection step. However, a particular challenge is predicting the relative importance of multi-type features. Therefore, bwsNMF was repeatedly executed with a set of weight parameters inside the parameter searching space (10-8, 10-6…,1) for each sl, to find the best set of parameters that can identify tumor subtypes for which patient survival was maximally different.
The datasets generated by TCGA are unique in that they have multilevel genomic profiles for the same patients and well-controlled clinical data including survival, drug response and histological characterization. We decided to use TCGA data to assess the effectiveness of our bwsNMF algorithm in regard to tumor subtype identification. We downloaded mutation data and RNA-Seq data of uterine corpus endometrial carcinoma from TCGA data portal (https://tcga-data.nci.nih.gov/tcga/) in August, 2013. The RNA-Seq data obtained from Illumina Genome Analyzer with RNASeqV2 protocol contained more than 20,000 genes and 370 tumor samples. We applied sNMF and bwsNMF for various input matrices built by different coding schemes to integrate different data types with η=1.
Snmf with Highly Varied Genes in RNA-Seq
We built a large biological network with published molecular interaction networks [19,20] to incorporate biological knowledge for tumor subtype identification. We tested a mutation indicator input matrix, of which each element was a fixed number for mutated genes and their neighbor genes (maximal depth=5 in the protein–protein interaction network), or a zero value for otherwise in a corresponding sample. This coding scheme was similar to, but still different from that of the network-based stratification (NBS) [15]. We did not apply any normalization to the indicator matrix. We used 194 mutated genes for which mutations occur in at least 50 times, which resulted in 833 genes (mutated genes + their neighbour genes). sNMF was repeatedly applied to the dataset with different values to obtain the most wellseparated survival curves among groups. In this case, three groups (group1: 208, group2: 134, group3: 28) were suggested, but they were not associated with overall survival (log-rank P=0.150). This could have several explanations. Some of patients did not have these mutations. This scheme does not consider the concentration of mutated genes or their neighbour genes. When some mutations observed in DNA exome sequences are very lowly expressed across patients, they might not generate any effect on the downstream pathways and not produce any power to discriminate patient groups. Some gain-of-function mutations became effective only by interaction with an important modifier-gene. When the modifier-genes were very lowly expressed across patients, the effect of the gain-of-function mutations was limited.
We tested another mutation indicator input matrix by selecting only 115 highly varying genes in the RNA-Seq profiles among 833 genes selected by the above scheme (i.e. frequently mutated genes and their neighbour genes). The first group (243 patients) usually did not have mutations of these genes or their neighbours. The second group (73 patients) had mutation neighbour genes (ENPP3, FOXJ1, LY6D, PRAP1 and SLCO2A1). Note that mutation neighbour genes instead of mutations determine this second group. The third group (54 patients) had many mutations and their neighbour genes in a protein–protein network, which was driven by mutations. The degree of association with overall survival was slightly better than the previous case (P=0.107). This observation supports the notion that it is meaningful to select mutations and their neighbour genes of which gene expression profiles were varied across samples because mRNA concentration of mutation genes or their binding partner may affect tumor progression and/or metastasis. However, using only mutations was not sufficient to inform overall survival.
Bwsnmf With RNA-Seq, Mutation Information, and Biological Networks
Because we hypothesized that including transcription factor target genes was important for clustering as well, we decided to include them and applied different weights on them with bwsNMF, because we had two different blocks and we did not know which block was more important for clustering. bwsNMF was used to cluster an input matrix with 115 genes highly varied in RNA-Seq profiles selected from 833 mutated genes and their nearest neighbor genes whose distance to a mutation was less than six in the protein-protein interaction network, and highly varied 235 target genes [20] of five transcription factors (MYC, CTCF, ESR1, ATF3, TP53). Thus, the total number of selected genes was 350. The input matrix has RNA-Seq expression levels for the transcription factor target genes and a fixed value (e.g., the largest RNA-Seq expression level) for mutations and their neighbors (called as mutation-related genes). When a gene was a transcription factor target gene and also a mutation-related gene, we used the fixed value to indicate that it was a mutation-related gene, although it was also a target gene. Interestingly, bwsNMF with this input matrix-coding scheme identified three novel subgroups highly associated with overall survival (log-rank P=0.009) (Figure 1). The number of patients for each subgroup was 206, 143 and 21. Figure 2 shows the basis/metagene matrix and the coefficient matrix obtained from bwsNMF. We only drew the discriminative genes that were differentially expressed between tumor types in the metagene matrix. The discriminative genes of group 1 were C4BPA, EDN3, PGR, SERPINA3 and SLC47A1, which were targets of ESR1. CBS, IGF2BP1,and FCHO1 were highly expressed in the second group, where CBS and IGF2BP1 were targets of MYC. Mutations and their neighbour were enriched in group 3. Each column of the coefficient matrix indicates the three-dimensional representation of a patient’s genomic profile. Figure 3 shows the sample-sample relationship with the threedimensional representations of the samples. sNMF with the same input matrix revealed three groups associated with overall survival at a lower level of significance (log-rank P=0.01). Collectively, using biological knowledge (mutated nodes, mutation neighbour nodes in a proteinprotein interaction network and a transcription target network) in combination with bwsNMF was very powerful in identifying new, clinically relevant subgroups of endometrial carcinoma.
Figure 1: Kaplan-Meier curves of overall survival for three clusters identified by block weighted sparse NMF with an input matrix of which elements have an indicator value for mutated genes and their nearest neighbors whose distance to a mutated gene was less than six in the protein-protein interaction network, and RNA-Seq gene expression values for highly varied transcription factor target genes.
Figure 2: Kaplan-Meier curves of overall survival for three clusters identified by block weighted sparse NMF with an input matrix of which elements have an indicator value for mutated genes and their nearest neighbors whose distance to a mutated gene was less than six in the protein-protein interaction network, and RNA-Seq gene expression values for highly varied transcription factor target genes.
Figure 3: The coefficient matrix obtained from our block weighted sparse NMF has the three-dimensional representations of samples. Each row of the coefficient matrix means the three-dimensional coordinate of this figure. H1, H2, and H3 are corresponding to the first, the second, and the third axis, respectively.
Here, we discuss the difference between our block-weighted sparse NMF and a graph regularized NMF-based approach. The network-based stratification (NBS) [15] used graph regularized NMF (GNMF) [21]
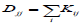 (9)
(9)
where A is the non-negative input (gene X patient) matrix, W is the basis/metagene matrix, H is the coefficient/loading matrix, L=D-K is graph Laplacian [22], where is a diagonal matrix whose entries are column sums of k 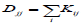 and K is the weight element of the ith row and the jth column, and Tr (∙) denotes the trace of a matrix. The term of Tr (W^T LW) constrains the column vectors of to give higher weight to local graph neighborhoods to take into account local graph topology around each mutated somatic gene. NBS used mutation information for tumour subtype identification. Its performance depends not only on network smoothing but also on NMF, because its performance was improved with NMF instead of HC [15]. NBS took advantage of somatic mutation information and a gene–gene interaction network by projecting mutations onto the network for the clustering of ovarian serous cystadenocarcinoma into four subtypes, lung adenocarcinoma into six subtypes, and endometrial carcinoma into three subtypes that are associated with patient overall survival or histological type. The most predictive data types were somatic mutations for ovarian cancer patient survival, somatic mutations and RNA-Seq for lung cancer patient survival, and copy number variations for endometrial cancer patient histological types [15], respectively. The minimization process of the objective function was similar to Lee and Seung’s multiplicative updating algorithm [23] that suffers from convergence issues. The network-regularized NMF code for NBS was extended from the NMF Matlab toolbox [8] partly to consider convergence issues, because this particular implementation was based on multiplicative update rules to obtain W and the non-negativity-constrained least squares or multiplicative update rules to obtain H. This implementation was helpful for handling convergence issues, but it still used multiplicative update rules at the one-side of alternating steps at least. In order to completely resolve the convergence issues, we need to find a way to avoid the multiplicative update rules. By contrast, our block weighted sparse NMF is based on the block coordinate descent method that generally shows faster convergence than multiplicative updating rules. The NBS approach does not have a way to apply different weights to different data types, and it does not use a transcriptional regulatory network. Our bwsNMF algorithm is an advanced form of sparse NMF, which is designed to apply different weights to heterogeneous data types, and our strategy for tumour subtype identification uses a transcription regulatory network, because target genes of transcription factors that are downstream effectors of somatic mutations may represent distinct biological subtypes.
and K is the weight element of the ith row and the jth column, and Tr (∙) denotes the trace of a matrix. The term of Tr (W^T LW) constrains the column vectors of to give higher weight to local graph neighborhoods to take into account local graph topology around each mutated somatic gene. NBS used mutation information for tumour subtype identification. Its performance depends not only on network smoothing but also on NMF, because its performance was improved with NMF instead of HC [15]. NBS took advantage of somatic mutation information and a gene–gene interaction network by projecting mutations onto the network for the clustering of ovarian serous cystadenocarcinoma into four subtypes, lung adenocarcinoma into six subtypes, and endometrial carcinoma into three subtypes that are associated with patient overall survival or histological type. The most predictive data types were somatic mutations for ovarian cancer patient survival, somatic mutations and RNA-Seq for lung cancer patient survival, and copy number variations for endometrial cancer patient histological types [15], respectively. The minimization process of the objective function was similar to Lee and Seung’s multiplicative updating algorithm [23] that suffers from convergence issues. The network-regularized NMF code for NBS was extended from the NMF Matlab toolbox [8] partly to consider convergence issues, because this particular implementation was based on multiplicative update rules to obtain W and the non-negativity-constrained least squares or multiplicative update rules to obtain H. This implementation was helpful for handling convergence issues, but it still used multiplicative update rules at the one-side of alternating steps at least. In order to completely resolve the convergence issues, we need to find a way to avoid the multiplicative update rules. By contrast, our block weighted sparse NMF is based on the block coordinate descent method that generally shows faster convergence than multiplicative updating rules. The NBS approach does not have a way to apply different weights to different data types, and it does not use a transcriptional regulatory network. Our bwsNMF algorithm is an advanced form of sparse NMF, which is designed to apply different weights to heterogeneous data types, and our strategy for tumour subtype identification uses a transcription regulatory network, because target genes of transcription factors that are downstream effectors of somatic mutations may represent distinct biological subtypes.
We reviewed the published survival analyses to assess the significance of endometrial cancer subtypes identified by various methods [15,24] from TCGA datasets. In the TCGA paper on endometrial carcinoma [24], somatic copy number aberrations (SCNAs) were hierarchically clustered into four groups associated with progression-free survival (log-rank P=0.0004) [24]. Multiple profiles were used to compare the four groups (POLE ultramutated, microsatellite instability (MSI) hypermutated, copy-number low, and copy-number high) associated with progression-free survival (log-rank P=0.02) [24]. The five clusters defined by RPPA profiles were highly correlated with histology (endometrioids, mixed, serous), grade and clusters defined by other platforms (mRNA three groups (mitotic, hormonal, immunoreactive), CNAs, DNA methylation four groups, microRNA, and MHL1 hypermethylation) [24]. MicroRNA profiles were clustered into six groups associated with overall survival (logrank P=0.18) [24]. iCluster revealed two groups (P=0.077 for overall survival, P=0.23 for recurrence-free survival) from somatic mutation, DNA copy number, DNA methylation, and mRNA expression data [24]. SuperCluster [24] identified four groups (hyper-mutator super cluster, low mutator endometrioid super cluster, ultra-mutator super cluster, serous super cluster), which showed association with cancer specific overall survival (P=0.0367) and progression-free survival (P=0.0265) [24]. However, any strong association between three groups identified from mRNA-Seq and patient overall survival or progression free survival has not been reported. Although NBS unveiled three subgroups associated with histological types of endometrial carcinoma [15], association with overall survival or progression-free survival was not reported.
In summary, we applied sNMF for sparser 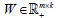 to a clustering problem and showed that it could identify tumor subtypes with clearer basis/metagene vectors by introducing more zeros in W. We developed a novel NMF algorithm of bwsNMF that could handle and assign different weights to heterogeneous datasets. We report three clinically relevant subtypes of the endometrial carcinoma, identified by bwsNMF by integration of mutation genes, mutation neighbor genes, and transcription factor target genes of mutation-related genes. The bwsNMF algorithm could be applied to other biomedical clustering problems with multiple heterogeneous data types.
to a clustering problem and showed that it could identify tumor subtypes with clearer basis/metagene vectors by introducing more zeros in W. We developed a novel NMF algorithm of bwsNMF that could handle and assign different weights to heterogeneous datasets. We report three clinically relevant subtypes of the endometrial carcinoma, identified by bwsNMF by integration of mutation genes, mutation neighbor genes, and transcription factor target genes of mutation-related genes. The bwsNMF algorithm could be applied to other biomedical clustering problems with multiple heterogeneous data types.