Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2009) Volume 2, Issue 3
Cross-species comparison of gene expression profiles allows deciphering fundamental and species-specific transcriptional programs of cells and offers insight into organization and evolution of the genome and genetic network. Here, we propose an algorithm for comparing microarray data from different species to unravel transcriptional modules that are conserved or divergent through evolution. The proposed algorithm is based on cross-species matrix decomposition that includes a nonlinear independent component analysis followed a generalized probabilistic sparse matrix factorization on microarray data from different species. The proposed algorithm captures transcriptional modularity that might result from highly nonlinear interactions among genes, and partitions genes into mutually non-exclusive transcriptional modules. The conserved transcriptional modules are identified by the latent variables that are associated with predominant biological prototypes shared across species. We illustrated the application of the proposed algorithm by an analysis of human and mouse embryonic stem cell (ESC) data. The analysis uncovered conserved and divergent transcriptional modules in the ESC transcriptomes, shedding light on the understanding of fundamental and species-specific regulatory mechanisms controlling ESC development.
Keywords: Comparative transcriptomics, Transcriptional modules, Generalized probabilistic sparse matrix factorization, Embryonic stem cells.
GPSMF: Generalized Probabilistic Sparse Matrix Factorization
ESCs: Embryonic Stem Cells
NICA: Nonlinear Independent Component Analysis
Given the completion of genomic sequencing of various mammalian and other organisms, transcriptomes of different species can be readily compared across species through the identification of orthologous genes (Ihmels et al., 2005; Li et al., 2007; McCarroll et al., 2004; Stuart et al., 2003). One of the most important and widespread mechanisms used by a cell in functional regulation is the coordinate modulation and interaction of genes. By organizing genes into different transcriptional modules, a living cell coordinates the activities of genes and carries out complex functions. Important sequence elements in the genome, as well as important biological processes or pathways, are often evolutionarily conserved (Ihmels et al., 2005; Li et al., 2007; Stuart et al. , 2003; Zhan et al., 2005). The comparative transcriptomics study allows uncovering transcriptional modules conserved or divergent through evolution, and has shown to be a powerful approach in deciphering fundamental or species-specific regulatory programs of cells and for insights into organization and evolution of the genome and genetic network (Alter et al., 2003; Bergmann et al., 2004; Ihmels et al., 2005; Li, et al., 2007; McCarroll et al., 2004; Stuart et al., 2003; Vallee et al., 2006; Zhou and Gibson, 2004). In most comparative transcriptomics analyses, linear correlations between genes are evaluated using conventional clustering methods such as hierarchical clustering, k-means, and SOM, and genes are partitioned into mutually exclusive modules (Atkinson et al., 2003; Ihmels et al., 2005; Li et al., 2007; Yuh et al., 1998; Zhou and Gibson, 2004). However, nonlinear interactions among genes are often observed in transcriptional networks, such as in negative feedback events or two consecutive biological events of threshold and saturation (Alter et al., 2000; Li et al., 2007). Moreover, a single gene may participate in multiple biological processes or pathway activities, so that belong to multiple transcriptional modules. In addition, the clusteringbased methods identify transcriptional modules by assuming that genes with similar expression profiles share similar functions or pathways. However, genes involved in the same biological process or pathway can have different expression patterns (Li, et al., 2007; Zhou et al., 2002). Different from clustering-based methods, matrix decomposition methods (e.g. singular value decomposition, independent components analysis, non-negative matrix factorization, network component analysis, and sparse matrix factorization) do not cluster genes based on the pair-wise similarity measurement in microarray data analysis (Alter et al., 2000; Carmona-Saez et al., 2006; Chiappetta et al., 2004; Dueck et al., 2005; Frigyesi et al., 2006; Kim and Tidor, 2003; Lee and Batzoglou, 2003; Liao et al., 2003; Liebermeister, 2002; Wang et al., 2006). In these methods, genes with related functions or regulatory programs can be clustered together even they have different expression profiles. A gene can be partitioned to multiple mutually non-exclusive modules if the gene participates in multiple biological processes or have multiple functions. However, the matrix decomposition methods use linear models, describing gene expression as linear combinations of latent biological sources, which is often not true for gene-gene relationships and gene expression data. To overcome the problem, we recently developed a twostage matrix decomposition method, which is based on a nonlinear independent component analysis (NICA) on the expression data, followed by probabilistic sparse matrix factorization (PSMF), for transcriptional module discovery (Li et al., 2007). The method combines both projection and model-based approaches and is free from both linear-models and similarity measurements, providing a more suitable solution for transcriptional module discovery from gene expression data.
In the present study, we extend the two-stage decomposition method to cross-species studies on gene expression data for uncovering transcriptional modules conserved and divergent through evolution. A generalized probabilistic sparse matrix factorization (GPSMF) approach is particularly proposed to simultaneously decompose two independent latent component matrices from different species. A framework is then implemented for identifying evolutionarily conserved and divergent transcriptional modules from the outcomes of GPSMF and NICA analyses. In comparison with another method, our algorithm can better uncover functionally relevant transcriptional module. We applied the newly developed methodology in analyzing gene expression data of embryonic stem cells (ESCs) from human and mouse. The results demonstrated that the new algorithm can unravel conserved and divergent modules that are significantly associated to ESC development, shedding light on fundamental and species-specific mechanisms controlling ESC self-renewal and differentiation.
The NICA Decomposition
Suppose we have two microarray data matrices X1∈ℜN1×Mand X2∈ℜN2×Mwith the same sample size M, where N1 and N2 are the numbers of genes in the two data sets, the microarray data can be described by the noisy nonlinear mixing model
X1=f1(S1)+O1
X2=f2(S2)+O2 (1)
where S1∈ ℜN1×M' and S2∈ ℜN2×M' denote the two latent source matrices, M' is the number of latent sources. O1 and O2 are the white Gaussian noise matrices. The nonlinear mappings f1(.) and f2(.) are modeled by a multilayer perceptron (MLP) network (Haykin, 1999) with one nonlinear hidden layer as:
f1=C1.tanh[S1.B1+D1]+E1
f2=C2.tanh[S2.B2+D2]+E2 (2)
where Bm and Cm are the weight matrices of the hidden and output layers, and Dm and Em are the corresponding bias matrices for m = 1,2.
Assuming that the source signals Sm at the input layer of the MLP network have simple Gaussian distributions, we obtain a nonlinear principal component analysis solution for Sm based on variational Bayesian learning for blind estimation and separation in the nonlinear mixture data model in Eq. (1). This solution models nonlinear mixtures (observed data), but provides no estimate of independent source signals.To find independent components from Sm, we apply a standard linear ICA to Sm using the Fast ICA algorithm (Hyvarinen and Oja, 2000). The goal of the linear ICA is to decompose Sm =S¯ m.Am so that columns (components) of S¯ mare statistically as independent as possible.
The GPSMF Model
The GPSMF approach we propose is a generalized extension of probabilistic sparse matrix factorization (nd used to decompose two data matrices simultaneously in comparative analysis of two microarray Dueck et al., 2005) adata sets. Given two matrices S¯ 1∈ℜN1×M′ and S¯ 2∈ℜN2×M′ derived from the NICA procedure, the GPSMF is to find Y1∈ℜN1×M′, Y2∈ℜN2×M′ and Z∈ℜL×M′ such that S¯ 1=Y1.Z and S¯ 2=Y2.Z . Here the columns of S¯ 1=Y1 and S¯ 2=Y2 represent independent latent components. N1 and N2 are the number of genes in the two data sets, M′ is the number of latent sources. Y1 and Y2 are factor weighting matrices. Each row of Y1 and Y2 has at most K non-zero entries. Row vectors of Z contain unobserved L latent factor profiles. Specifically, let kim be the number of non-zero entries ( kim ≤ K ) of the row vector yim∈ℜ1×L in Ym and lim=(li1,li2,...,likim) be the vector that contains column indices of non-zero entries of yim, where m=1, 2 for two data sets, we model each gene “hidden” expression profile across the independent latent component S¯ im∈ℜ1×M′ as a linear combination of kim of the factor profiles zl∈ℜ1×M′ plus noise:

Supposing the noise is Gaussian with variance σim2 for S¯ im,then the likelihood of S¯ im can be written as:
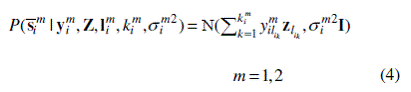
Assume that zl is normally distributed, lim is uniformly distributed, and kim is multinomially distributed. Multiplying these priors by Eq. (4) forms the joint distribution P(S¯ m,Ym,Zm,Lm,Km|Σm ) . From the joint distribution, we first estimate elements in Y1 and Z by utilizing a factorized variational inference method (Dueck et al., 2005; Jordan et al., 1999) from S¯ 1 that contains the independent latent components in the primary (“reference”) organism. Then, we estimate elements in Y2 by the same method from S¯ 2 that contains the independent latent components in the second (“target”) organism and Z.
When applying the GPSMF, the choices of the parameters L and K affect the structure of decomposition. L is the predefined number of possible latent variables that determines the number of modules identified by our algorithm. L should be much smaller than N1 and N2 (i.e. total gene numbers in the two data sets), since the expression of most genes is thought to be influenced by a small set of genes that act in combination as key regulators or network hubs to maintain the overall expression pattern of a transcriptional module. K is the maximum number of “effective” latent variables and should be less or equal to L. In the case of K = 1, each row in the data matrix is associated with only a single factor, and the sparse matrix factorization is a clustering of the data rows. When K = L, the factorization is simply a low rank approximation. Since our assumption is that the expression of each gene is determined by only a small set of possible key genes, we heuristically set K = 3 in our study
Identification of Conserved and Divergent Modules
Given the factor weighting matrices Y1, Y2, and the factor profile matrix Z, we propose an approach for identifying conserved and divergent transcriptional modules. Let us define
setAl := (orthologous geneID1[i1], satisfy yi1l1≠0, for i1=1....,N1)
setBl := (orthologous geneID2[i2], satisfy yi2l2≠0, for i2=1....,N2)
where yi1l1 and yi2l2 are the elements of Y1 and Y2, respectively, l =1,...,L . We then determine 1) conserved transcriptional modules as the common orthologous genes in both setAl and setBl (i.e., set Al∩ set Bl ); 2) divergent modules in the primary organism as the orthologous genes in setAl but not in setBl (i.e., set Al - set Bl ); and 3) divergent modules in the second organism as the orthologous genes in setBl but not in setAl (i.e., set Bl - set Al ).
Cross-species Matrix Decomposition of Microarray Data
Fig. 1 shows a general schema of the proposed algorithm. The algorithm is based on two-stage matrix decomposition on two microarray datasets from different species to identify conserved or divergent transcriptional modules. We first apply the NICA transformation to capture the nonlinear structure in the data and represent the data with independent latent components. We then apply GPSMF to simultaneously decompose the two independent latent component matrices of different species. We finally identify conserved and divergent transcriptional modules from the outcomes of the matrix decomposition.
Figure 1: A general framework of the proposed algorithm
From orthologous gene expression profile data sets X1 (N1 genes and M samples) in organism A and X2 (N2 genes and M samples) in organism B, the NICA extracts nonlinear independent components (columns in S̄1 and S̄2 ). At the GPSMF stage, S̄1 and S̄2 are jointly approximated by the product of sparse matrix Y1 and low-rank Z and the product of sparse matrix Y2 and Z, respectively. The values of all matrices are color coded by using a color heatmap, from dark green (minimum) to dark red (maximum). In the clustering process, conserved and divergent gene modules are identified by finding the common and different orthologous genes corresponding to nonzero indices of each column of Y1 and Y2.
The NICA method that we adopt is based on a variational Bayesian learning (Jutten and Karhunen, 2004; Lappalainen and Honkela, 2000). The method uses a multilayer perceptron (MLP) network as a nonlinear mapping to model nonlinear mixtures of data. The MLP network can model any nonlinear mapping from sources to observed data with certain accuracy, given enough nodes in the hidden layer (Haykin, 1999). The MLP network also provides a flexible nonlinear mapping because its model complexity scales linearly with the dimension of the latent source space (Lappalainen and Honkela, 2000).
The GPSMF approach we propose is used to simultaneously decompose two matrices derived from the NICA procedure on microarray data of different species. The GPSMF models the expression profiles in each species as a linear weighted combination of profiles from a small number of prototypes that represent the influence of different biological or experimental factors shared by the two species. The GPSMF modeling is based on the following assumptions: a) the expression of each orthologous gene responding to experimental conditions is equivalent in both species; b) the expression profile of a gene is determined by a linear combination of hidden biological sources or variables, represented by the latent components; and c) the two species examined share, to a certain degree, a small set of biological prototypes that have predominant influence on the expression patterns of most of genes. The GPSMF procedure is appropriate for modeling gene expression data across species, since while many genes are involved in gene regulation, a small set of transcriptional regulators or network hub genes have a predominant impact on the overall expression patterns of most of genes. The biological prototypes with the predominant impact and their activities are either conserved across species or divergent, which provides a basis for the identification of conserved and divergent transcriptional modules in our algorithm. The conserved transcriptional modules are likely related to fundamental biological processes, pathways or molecular mechanisms. The divergent modules are suggestive of species-specific transcriptional programs.
Transcriptional Modules in Embryonic Stem Cells
The gene expression in embryonic stem cells (ESCs) is carefully regulated so that the cells either maintain the pluripotent state by self-renewal or undergo differentiation. An understanding of gene regulatory mechanisms is essential for realizing the great potential of ESCs in regenerative medicine. The Oc4/Sox2/Nanog-directed network is a central regulatory circuitry controlling ESC self-renewal and differentiation (Boyer et al., 2005; Loh et al., 2006; Sun et al., 2006; Zhan, 2008; Zhan et al., 2005). However, whether there are fundamental or species-specific mechanisms underlying the activity of this critical network in ESCs has not been adequately explored. As described above, our method is particularly designed for identifying conserved and divergent transcriptional modules in which a small set of prototypes (e.g. transcriptional factors or network hub genes) control the overall expression pattern. The method is thus suitable for analyzing the Oct4/Sox2/Nanog-directed regulatory network for insight into fundamental and species-specific mechanisms in regulating ESC development.
For the analysis, we selected 1681 orthologous genes bound by Oct4, Sox2 and Nanog in human and mouse genomes, and examined their expression profiles determined from multiple cell lines of undifferentiated ESCs and their earliest differentiated counterparts, embryoid bodies (EBs). Totally 18 samples were examined for human and mouse cells, respectively. The human microarray data were obtained from our previous studies on ESCs and other publications (Li et al., 2006; Li et al., 2007; Liu et al., 2006; Sato et al., 2003). The mouse microarray data were obtained from the GEO database (accession numbers: GSE3231, GSE2972 and GSE3749) (http:// www.ncbi.nlm.nih.gov/geo). The expression data determined by BeadArray were normalized using the quantile method, and the data by Affymetrix were normalized using the RMA method. The expression data were then converted into log2 ratios of expression values over the average expression value for each gene. The missing data in the data sets were filled by KNN imputing. Human and mouse orthologous genes were obtained from the Affymetrix human- mouse ortholog links.
In the analysis, we set the number of independent latent components equal to the number of experimental conditions for simplicity. We set the number of hidden neurons in the MLP network as twice as the number of independent latent components for an accurate nonlinear mapping. We also set K to 3 and L to 3 through 10 in the computation. For each identified transcriptional module, we identified biological processes or pathways that were significantly over-represented, using the Fisher’s exact test followed by the false discovery rate adjustment. Fig. 2 shows the identified conserved and divergent transcriptional modules with heatmap presentations of the expression profiles. The gene list of each transcriptional module is provided in Supplementary File 1.
Figure 2: Heatmap of conserved and divergent transcriptional modules
Gene expression profiles of conserved (C1, C2, C3) and divergent (D1, D2, D3) transcriptional modules identified from Oct4/Sox2/Nang-directed network genes in human and mouse ESCs. Each module is presented by a heatmap of the expression profile (red: gene up-regulated in comparison with the mean, green: gene down-regulated, black: no change on the expression level).
We identified three conserved and three divergent transcriptional modules that showed distinctive expression patterns (Fig. 2 - C1, C2, C3, D1, D2, D3; Supplementary File 1). The conserved module C1 showed repressed expression in undifferentiated ESCs of both human and mouse, as illustrated by the heatmap (Fig. 2- C1). The module, composed of 401 genes, was enriched by genes involved in development (27.3% of the total genes in the module, p-value 2.52×10-20), morphogenesis (14.04%, p-value 5.92×10-12), and cell differentiation (13.5%, p-value 2.24×10-11). Embryonic development (p-value 4.93×10-7), mesoderm development (p-value 2.70×10-3), cell proliferation (p-value 2.61×10-5), pattern specification (p-value 3.70×10-5), embryonic pattern specification (p-value 1.50×10-3), and apoptosis (p-value 1.60×10-3) were particularly enriched in this module. Also included in this module were members of the Wnt pathway (p-value 6.87×10-5; including Jun, GSK3b,Dkk1, Fzd1, Fzd2, Fzd8, Sfrp1, and Tbl1x), BMP pathway (p-value 2.70×10-3; including Twsg1, Tob1, Gpc3, Bmp2,Prss11), TGFb pathway (Bmp2, Bmp5, Bmpr2, Smad3, Id2,and Pitx2), JAK-STAT pathway (Bcl2l1, Cntfr, Pias4, Stat2,and Stat3), and PI3K pathway (Eif2ak3, Pik4ca, Pip5k1c,and Pik3r1). All these enriched biological processes and signaling pathways are critical for ESC development (Li et al., 2007; Sun et al., 2006). In addition, the module contained 30 transcription factors, including Hand1, GATA6 and ZIC1, which are know to be repressed in ESCs of both human and mouse (Li et al., 2007; Sun et al., 2006). The conserved module C2, on the other hand, showed elevated expression in undifferentiated ESCs of both human and mouse (Fig. 2 - C2). This transcriptional module, containing 67 orthologous genes, was enriched by genes participating in cell cycle (14.7% of the module genes, p-value 2.11×10-4) and regulation of biological process (38.2%, p-value 2.71×10-5). The conserved transcriptional module C3, however, showed a mixed expression pattern in both human and mouse ESCs (Fig. 2 - C3). The module contained 28 genes, mainly participating in metabolism (67.9%, p-value 1.30×10-3). The module also included members of the Wnt pathway (Myc,Senp2, Ppp2r1a). The divergent transcriptional modules, on the other hand, shared little similarities between human and mouse ESCs on the predominant regulatory programs. The divergent module D1 showed transcriptional modularity in human but not in mouse ESCs, as illustrated by the heatmap (Fig. 2 - D1). The module, composed of 106 orthologous genes, showed repressed expression in undifferentiated ESCs in human but little transcriptional changes during ESC differentiation in mouse. The genes of the module were mainly involved in development (26.4% of the total genes in this module (p-value 1.29×10-5) and morphogenesis (16.9%; p-value 1.48×10-5). Also enriched in the module were pattern specification (p-value 5.55×10-4), cell differentiation (pvalue 4.80×10-3) and cell fate commitment (p-value 1.40×10-2). The module included six transcription factors: Lef1,Hoxb5, Hoxb6, Hoxb9, Hoxc5 and Rax, all of which were related to development. The module also included members of the TGFb pathway (Bmp4, Thbs3, and Inhba). The divergent module D2, on the other hand, showed transcriptional modularity in mouse but not in human ESCs (Fig. 2-D2). The module consisted of 59 orthologous genes, which were repressed in undifferentiated ESCs in mouse but showed no consistent trend of expressional changes in human ESCs. The module was enriched by genes participating in development (25.4%, p-value 3.60×10-3) and morphogenesis (15.6%, p-value 8.60×10-3), including embryonic development (p-value 1.50×10-2) and pattern specification (p-value 2.60×10-3). Also enriched were the BMP signaling pathway (p-value 3.40×10-3) and TGFb signaling pathway (p-value 6.00×10-3; including ligand Bmp7, receptor Acvr1b,and signal transducers Smad1 and Smad 5). The divergent module D3, strikingly, showed transcriptional modularity of opposite transcriptional trends between human and mouse ESCs (Fig. 2 - D3). The 43 orthologous genes of this module were over-expressed in mouse ESCs while under-expressed in human ESCs. The module was mainly enriched by genes involved in translation (14.0%, p-value 5.24×10-5), particularly translational initiation (9.3%, p-value 2.52×10-4) and regulation of translational initiation (7.0%, p-value 1.00×10-3).
The conserved and divergent transcriptional modules underlie the fundamental and species-specific gene regulatory mechanisms in ESCs. The results of this study suggest that the Oct4-Sox2-Nanog-directed regulatory network is not only responsible for primary “stemness” properties of ESCs, but also maintains species-specific programs in regulating pluripotency. The results are consistent with the fact that significant differences exist on the potential targets of Oct4, Sox2 and Nanog between human and mouse, despite of a certain overlap (Loh et al., 2006).
Comparison with Generalized Singular Value Decomposition(GSVD)
A GSVD-based matrix decomposition method was previously proposed for cross-species analysis of gene expression data (Alter et al., 2003). Different from our method, the GSVD method is based on a linear model and one-step matrix decomposition, conducted by singular matrix decomposition. We compared our method with the GSVD method through analysis on the same set of ESC expression data to further evaluate our method. We firstly identified three conserved modules and three divergent modules using the GSVD method, as we did by using our method, from the human and mouse ESC data. We then conducted functional analyses on each of the identified modules, using DAVID tools (Huang et al., 2007). Table 1 shows the statistical enrichment of functional categories in the transcriptional modules identified by both methods. The functional categories included Gene Ontology (GO) terms, protein-protein interactions, protein functional domains, bio-pathways, and literatures. The enrichment level was calculated by transforming the enrichment p value after FDR correction to a negative log value and averaged over all functional categories for corrected p < 0.05. If no functional categories were found for corrected p < 0.05, the smallest value of corrected p was taken for calculating the enrichment level. As illustrated, our method outperformed the GSVD method on the functional enrichment in both the conserved and divergent modules. This implies that our method can better identify functionally coherent transcriptional modules that are either conserved or divergent through evolution
| Our method | GSVD-based method | ||
| Gene module | Enrichment level | Gene module | Enrichment level |
| Conserved modules | |||
| C1 (401 genes) | 3.63 | C1 (250 genes) | 3.08 |
| C2 (68 genes) | 3.32 | C2 (74 genes) | 2.47 |
| C3 (28 genes) | 1.87 | C3 (39 genes) | 1.66 |
| Averaged over conserved modules | 2.94 | Averaged over conserved modules | 2.40 |
| Divergent modules | |||
| D1 (106 genes) | 1.44 | D1 (101 genes) | 1.25 |
| D2 (59 genes) | 1.07 | D2 (57 genes) | 0.84 |
| D3 (43 genes) | 2.30 | D3 (44 genes) | 1.68 |
| Averaged over conserved modules | 1.60 | Averaged over conserved modules | 1.26 |
Table 1: Comparison with the GSVD method based on DAVID functional analysis
Three conserved modules and three divergent modules identified by each method were evaluated. The functional enrichment level in each gene module is calculated by transforming the enrichment p value after FDR correction to a negative log value and averaged over all functional categories for corrected p < 0.05. If no functional categories are found for corrected p < 0.05, the smallest value of corrected p is taken for calculating the enrichment level.
The method presented in this study demonstrates success in identifying evolutionarily conserved and divergent transcriptional modules. Nevertheless there remain limitations of the reported method. For example, the current approach can only apply to microarray data of two species. Moreover, challenges still remain in designing in vitro or in vivo experiments to validate the results predicted by ours or other approaches. In the further research, we will extend our approach to compare more than two species. We will also integrate gene expression data with transcription factor binding information into this method to identify TFmediated regulatory modules conserved or divergent across species. This would allow experimental validation of genes in a regulatory module by either ChIP methods or RNAi– mediated depletion of the specific transcription factors.
In this study, we present an algorithm for cross-species analysis of microarray data to address the challenge of discovering transcriptional modules conserved and divergent through evolution. The proposed algorithm tackles two microarray data sets from different species as inputs, imposing two-stage matrix decomposition on the microarray data, firstly by NICA and then by GPSMF. The new algorithm captures transcriptional modularity that might result from highly nonlinear interactions among genes, and partitions genes into mutually non-exclusive transcriptional modules. The conserved transcriptional modules are identified by the latent variables that are associated with predominant biological prototypes shared across species. The identified transcriptional modules are highly associated with biological functions, in comparison with those identified by another method. As demonstrated by the analysis on human and mouse ESC data, the newly developed methodology can identify evolutionarily conserved and divergent transcriptional modules and facilitate the comparative transcriptomics studies.
This study was supported by the Intramural Research Program, National Institute on Aging, NIH.