Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2016) Volume 9, Issue 1
The past decade has seen a rapid growth in the application of mathematical and computational tools for extracting insight from biological networks, and of particular interest here, visualising the community structure within such networks. Clustering approaches have proven useful methods to uncover structural and functional sub-groups from within protein interaction networks. However many commonly used clustering methods for identifying functionally relevant substructures within molecular networks do not perform well with increasing network sizes.
We tested the performance of algorithms in terms of their ability to identify functionally relevant sub-clusters within networks of varying size as well as computational performance. Our studies suggest many algorithms perform well on smaller networks but fail to scale with network size. A Spectral based Modularity clustering algorithm, with a fine-tuning step, provided both scalability and improved identification of clusters enriched for functional annotation (e.g. disease) in real proteomic interaction datasets.
Keywords: Community detection, Modularity, OpenMP, Systems biology, Proteomics, PPI networks, Functional enrichment
The detection and analysis of community structure in networks has received considerable attention in recent years [1-3]. Community structure based clustering is the division of a network into groups of nodes with relatively dense connections within the group and sparser connections to other groups in the network. In many networks, finding the underlying groups provides practical and important information. Groups within social networks for example, may correspond to social units; in biological networks it helps to reveal substructures with common functionality or association with diseases [4-6]. Many algorithms now exist to solve the problem of breaking up the network into its communities, but most struggle to scale with current biological datasets.
We focused on a sub-set of community detection algorithms, with the goal of applying these to protein interaction networks. Nodes in these networks represent biomolecules, such as genes or proteins, and the edges the structural or protein interactions connecting them. We implemented in C++ a suite of three algorithms, optimised for the scalable analysis of large interaction networks based on the Modularity measure containing: Geodesic and Random Walk edge Betweenness, and Spectral Modularity; we also include a Cytoscape [7] App (version 3.0) for the Spectral Modularity algorithm. We tested the suite’s performance on synthetic networks, on the scale of 1000 proteins to represent realistic biomolecular complexity on multi-core workstations. We also tested the suite’s clustering performance on two previously published datasets [8,9], and investigated the enrichment of the clusters obtained for functional annotations and common neurological and neurodevelopmental diseases/disorders. Evaluation of enrichment was performed using a combination of Hypergeometric and permutation tests. We evaluated the robustness of clusters found with our suite’s boot-strap facility, and against commonly used Modularity based clustering algorithms available [10,11].
Synthetic networks were generated using the [12] benchmark and modelled on the order of 1000 proteins and 5000 interactions as described in Table 1 (Networks 2, 3 and 4, see also Supplementary Table S1). Three previously studied biological datasets were included. The MASC complex, representing a protein complex surrounding the mammalian NMDA receptor [8] consists of 101 proteins and 246 interactions (Network 1 in Table 1, see also Supplementary Table S2). The second, from a list of 1461 proteins obtained from a study of the PostSynaptic Density (PSD) in the human brain [9]. Protein-protein interactions were obtained by mining publicly available databases: HIPPIE [13], BioGRID [14], IntAct [15] and performing an InterologWalk over different species using Bio::Homology::InterologWalk [16]. This second network (Network 5 in Table 1, see also Supplementary Table S3) consists of 1312 proteins and 8031 protein interactions. The third is the Human interactome network BioPlex [17]. This network (Network 6 in Table 1, see also Supplementary Table S7) contains 7668 proteins and 23744 protein interactions, found using high-thoughput affinitypurification mass spectrometry in human embryonic kidney (HEK) 293T cells.
| Network | Nodes | Edges | PPI dataset |
|---|---|---|---|
| Network 1 | 101 | 246 | MASC complex |
| Network 2 | 493 | 1971 | Synthetic Pre-Synaptic Density |
| Network 3 | 855 | 4182 | Synthetic Pre-Synaptic Density |
| Network 4 | 1108 | 4691 | Synthetic Post-Synaptic Density |
| Network 5 | 1312 | 8031 | Human PSD |
| Network 6 | 7668 | 23744 | BioPlex network |
Synthetically generated networks (Networks 2, 3 and 4) showing the number ofNodes and Edges. These networks are based on unpublished proteomic studies.Networks 1, 5 and 6 are taken from published studies [8,9,17] respectfully. Finalcolumn gives the networks commonly referred to dataset name.
Table 1: Network.
Modularity (Q) measures the quality of a particular network division into communities. It measures the number of edges found within the communities relative to the expected number of edges within the communities, if these edges had been placed at random. The Modularity based algorithms we implemented [18,19] are largely designed for single workstation deployment which is not ideal for bootstrap analysis of large networks. Further we found no readily available implementation of the Random Walk algorithm [18]:
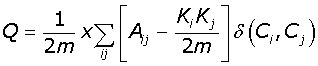 (1)
(1)
In eqn-1 the degree of the ith vertex is given by 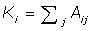 . Where Aij is the interaction matrix, m the total number of edges in the network and the final term the Kronecker delta function, which equals 1 if the ithand jthnodes fall into the same community and 0 otherwise. The maximum value of Modularity is 1, with typical values for real networks ranging from 0.3 to 0.7. We can optimise clustering in the Geodesic and Random Walk algorithms by searching for the global maximum.
. Where Aij is the interaction matrix, m the total number of edges in the network and the final term the Kronecker delta function, which equals 1 if the ithand jthnodes fall into the same community and 0 otherwise. The maximum value of Modularity is 1, with typical values for real networks ranging from 0.3 to 0.7. We can optimise clustering in the Geodesic and Random Walk algorithms by searching for the global maximum.
The third algorithm, Spectral Modularity, makes use of the spectral properties of the network [19]. The spectral properties are obtained using the Modularity matrix (B) using eqn-2:
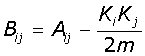 (2)
(2)
The network is expressed in terms of its eigenvectors and eigenvalues and recursively partition into two communities; positive values of the eigenvector giving a set of nodes belonging to one community, and the negative values to another. The partition can be expressed as a column vector (S) of the nodes with values ± 1. Partitioning occurs if the maximum positive eigenvalue is greater than the tolerance (10-5) for the current partition, and if it results in a positive contribution to the Modularity. The change in Modularity is calculated from this leading eigenvector and the generalised Modularity matrix (B(g)) for the split is given by eqn-3:
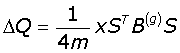 (3)
(3)
where the generalised Modularity matrix for a given split is expressed as,
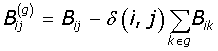 (4)
(4)
Given an initial separation using the Spectral method, it is possible to maximise for the change in Modularity using a fine-tuning step. The first stage here is to find the node which, when moved from one community to the other, gives the maximum change in Modularity. This node’s community is then fixed and we repeat the process until all nodes have been moved. The whole process is repeated from this new state until the change in the Modularity, between the new and old state, is less than the predefined tolerance. Our implementations were tested on the widely used benchmark, Zachary’s “karate club” network, which represents observed social patterns between members in a university sports club. Our implementations reproduced the results as reported in [18,19].
The suite is designed to run on computing clusters and includes a boot-strap facility, allowing a random sub-sample of the data to be selected; currently set to 80% of the network’s node size. Sampling from multiple bootstrap runs allows the robustness of each algorithm applied to the data to be investigated. The package clusterCons [20] has been used in conjunction with the suite, to build a consensus matrix from which to test the robustness of discovered communities, and proteins found inside each community.
Our implementations were found comparable in terms of speed and scalability with other implementations, when a direct comparison could be made, as shown in Figure 1a. However, performance of the sequential Geodesic and Random Walk implementations was found inadequate over our datasets, as shown in Table 2. To improve their performance required re-programming, by parallelising the implementations using OpenMP. This allows the implementations to make use of the multiple processors on common a workstation, and still remain portable to run on computing clusters. The OpenMP implementations of the Geodesic and Random Walk algorithms parallelise the betweenness score calculations of the edges. Both implementations were tested and found to perform optimally for multi-cores as discussed in Section Speed and Scalability.
Figure 1: CPU-time verses network size for the Geodesic and Random Walk edge Betweenness algorithms.
CPU-time verses number of network edges for Geodesic (A) and Random Walk (B) implementations as given in Table 2. Showing R’s igraph package [10] implementation (crosses), single core (circles), 4 cores (squares), 8 cores (up-triangles) and 12 cores (down-triangles). Figures show both implementations scale to large network size using multiple cores. Figure (B) shows the sequential Random walk implementation unscalable at largest network size, and a predicted linear time (dotted line) given.
| Algorithm | Network 1 | Network 2 | Network 3 | Network 4 | Network 5 | Network 6 |
|---|---|---|---|---|---|---|
| Geodesic | 0.02 | 0.73 | 2.71 | 4.91 | 28.30 | - |
| Geodesic ( R ) | 0.03 | 0.28 | 1.38 | 3.00 | 24.60 | - |
| Random Walk | 0.05 | 212.0 | 1930.0 | 9690.0 | - | - |
| Spectral | 0.006 | 0.034 | 0.2 | 0.4 | 0.75 | 253.0 |
| FC | 0.002 | 0.0013 | 0.002 | 0.002 | 0.004 | 0.25 |
| SG1 | 0.04 | 2.03 | 3.54 | 6.10 | 5.7 | 75.0 |
CPU-time (in minutes) on a single core for Geodesic (and igraph’s R implementation), Random Walk, and Spectral Modularity algorithms. CPU-times are also given for the popular Modularity based clustering algorithms, the fast-greedy community algorithm (FC) [36] and coupled Potts model and simulated annealing algorithm with gamma set to 1.0 (SG1) [39,40]. No timing information was available for the fast-greedy community algorithm (GLay) [37].
Table 2: Single core CPU-times.
A quantitative and qualitative discussion of our suite’s clustering performance applied to the MASC, human PSD and BioPlex datasets is given in Sections MASC network, Human PSD network and BioPlex network. For this we made use of the functional annotation studies [8,21] and the topOnto package (https://github.com/statbio/topOnto), to perform the disease ontology enrichment analysis. Annotation enrichment of the clusters was carried out using a combination of the Hypergeometric test and permutation study as described in Section Clustering Performance. We find our implementations reproduce results found in the MASC network study, whilst our Spectral Modularity algorithm out performs others when applied to the human PSD network. The increase in diverse functional clusters, found in the human PSD network, with our Spectral Modularity algorithm is a result of our fine-tuning step as discussed in Section Comparison with Existing Cluster Algorithms. We further tested and compared the clustering performance of our suite’s Spectral Modularity algorithm on the larger BioPlex network [17].
Speed and scalability
We checked the suite’s performance against single and multi-core instances (2.4 GHz Intel Xeon “Westmere” with 12-cores) using gcc version 4.4.7. Table 2 details the CPU time in minutes for each algorithm with respect to varying sized synthetic networks as given in Table 1. Figure 1 shows the execution times for the sequential and OpenMP implementations of the Geodesic and Random Walk algorithms (see Supplementary Table S1 for details). Our Geodesic edge Betweenness algorithm was tested against the current known R implementation [10] with comparable performance (Figure 1a). For the Random Walk algorithm on Network 5, the execution time using a single core was over 14 days (20160 minutes), a limit beyond which the algorithm was considered unscalable. The predicted time of 26 days (37889 minutes) is shown by the dotted line in Figure 1b. For Network 4, the Random Walk algorithm took approximately 5 days (6827 minutes) to complete. This execution time dropped to 23 hours (1360 minutes) using the OpenMP implementation with 12 cores. As illustrated in Figure 1 there is no significant performance difference for networks smaller than 600 nodes (or less than 4000 edges). For networks larger than this size the performance difference is significant.
Clustering performance
The performance of each algorithm on the MASC and human PSD networks was studied. Tables 3 and 4 summarise the results with clustering consistency tested using the Normalised Mutual Information (NMI) and Adjusted Rand Index (ARI) metrics to the MASC and human PSD networks respectively. The original MASC study provides an analysis of the organisation and underlying functionality of the modularised MASC complex, clustered using the Random Walk algorithm and shown in the Figure 3 of [8]. We replicated this using our Random Walk algorithm in Figures 2a, and with our Spectral Modularity algorithm as shown in Figure 2b, visualised using the package Visone [22]. We generally find one or two large clusters (coloured in blue) containing molecules commonly associated with signal processing. Feeding into these are the primary signal reception clusters (coloured in red), formed around ionotropic and metabotropic receptors. Also feeding into signal processing clusters are several intermediate clusters (coloured in orange) regulate overlapping sets of pathways, and numerous clusters (coloured in green) are enriched for common downstream effector pathways.
| Algorithm | Modularity (Q) | No: Communities | CPU-time | NMI | ARI |
|---|---|---|---|---|---|
| Geodesic | 0.45 | 14 | 0.02 | 0.78 | 0.68 |
| Geodesic (R) | 0.45 | 14 | 0.03 | 0.78 | 0.68 |
| Random Walk | 0.47 | 13 | 0.05 | 1.0 | 1.0 |
| Spectral | 0.45 | 13 | 0.006 | 0.69 | 0.4 |
| FC | 0.48 | 8 | 0.002 | 0.72 | 0.52 |
| SG1 | 0.48 | 10 | 0.04 | 0.75 | 0.56 |
| Glay | 0.68 | 7 | - | 0.73 | 0.53 |
Maximum Modularity (Q), number of detected communities (C), sequential CPU time (in minutes) for each algorithm applied to the MASC complex in Table 1. The Normalised Mutual Information (NMI) and Adjusted Rand Index (ARI) metrics relative to the clustered MASC complex is given for each algorithm.
Table 3: Algorithm characteristics applied to MASC complex.
| Algorithm | Modularity (Q) | No: Communities | CPU-time | NMI | |||||
|---|---|---|---|---|---|---|---|---|---|
| G | R | S | FC | SG1 | Glay | ||||
| Geodesic (G) | 0.27 | 533 | 5.70 | 1.0 | 0.87 | 0.69 | 0.47 | 0.51 | 0.45 |
| Random Walk (R) | 0.18 | 738 | 8362.0 | 0.87 | 1.0 | 0.69 | 0.48 | 0.50 | 0.45 |
| Spectral (S) | 0.36 | 60 | 0.75 | 0.69 | 0.69 | 1.0 | 0.39 | 0.46 | 0.36 |
| FC | 0.38 | 37 | 0.004 | 0.47 | 0.48 | 0.39 | 1.0 | 0.37 | 0.45 |
| SG1 | 0.38 | 23 | 5.7 | 0.51 | 0.50 | 0.46 | 0.37 | 1.0 | 0.43 |
| GLay | 0.65 | 31 | - | 0.73 | 0.45 | 0.45 | 0.47 | 0.45 | 1.0 |
Maximum Modularity (Q), number of detected communities (C), sequential CPU time (in minutes) and the Normalised Mutual Information (NMI) metric for each algorithm applied to the human PSD network in Table 1.
Table 4: Algorithm characteristics applied to human PSD network.
Figure 2: Clustering of the MASC complex.
Clustering of the MASC PPI dataset [8] using the Random Walk edge Betweenness (A) and Spectral Modularity (B) algorithms. Protein communities have been colour coded in accordance with the clustering found in Figure 3 of [8]. Here red coloured communities (1 and 2) indicate proteins involved in input, blue (community 3, and 4 in (B)) information processing, orange communities (4 and 5 in (A), 5 and 6 in (B)) for sets of pathway outputs, and the remaining green communities for specific individual effector responses. The Spectral Modularity algorithm (B) captures many of the clustering results found in [8], and shown in (A). Key difference includes the separation of the central processing unit (community 3 in (A)) into two (communities 3 and 4 in (B)), diversifying communication between communities.
Figure 3: Clustering of the human PSD network.
The human PSD network is shown as a furball (A) with 291 Schizophrenia related genes, as given in Table 5, highlighted in magenta. Clustering from commonly available algorithms (Random Walk, Geodesic, Walktrap and MCL algorithms) tends towards many single (or two gene) communities, the MCL (B) algorithm is shown. Algorithms also tend towards the other extreme, generating a small number of communities of large size. These include the FC, SG, GLay and LEC (D) algorithms. Clustering results from our implementation of the Spectral Modularity (C) algorithm is shown to lie between these two extremes. Further details for each algorithms clustering characteristics can be found in Table 8.
For each cluster in the MASC and human PSD network found, we further tested the significance of enrichment for function and disease, using the Hypergeometric distribution formula for sampling without replacement:
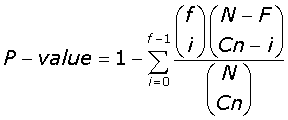 (5)
(5)
Where in eqn-5 N is the total number of genes in the network; Cn the number of genes in the community; F the total number of functional annotated genes in the network, and f the number of functional annotated genes per community. P-values, ≤ 10-2, were tested for their strength of significance (sig), by recording the percentage of P-values found from every community/annotation combination, lower than or equal to the observed P-value, when 1000 random permutations of the annotation labels were made. P-values found with a strength of significance <5% where consider statistically significant. P-values lower than the more stringent Bonferroni correction at the 0.05 significant levels is highlighted throughout the enrichment tables.
Performance of the suite’s boot-strap facility was also tested on the MASC and human PSD datasets. We ran each implementation on a distributed computing facility provided by ECDF (Edinburgh Compute and Data Facility, U of Edinburgh. 2013, www.ecdf.ed.ac.uk) 500 times, randomly selecting 80% of the network node size each time. The package clusterCons [20] was used in conjunction with the suite, to build a consensus matrix from which to test the robustness of discovered communities, and proteins found inside the communities. Community and protein robustness values range from 0, indicating no confidence in existing to 1, indicating absolute confidence in the cluster existing.
MASC network
We first discuss the clustering performance of the MASC network. Supplementary Table S4 gives the community enrichment values for the three algorithms relative to the functional family, sub-family, disease and phenotype annotation as found in the original MASC study [8]. The community enrichment values confirm the expected similarity between the Geodesic and Random Walk algorithms, and agree with the enrichment results reported in [8]. For example, community 2 in Supplementary Table S4 for the Geodesic algorithm and Random Walk algorithm appears to be enriched with proteins annotated as involved in G-protein coupling and in Depression. Similarly community 4, is enriched for Erk1/2 MAP kinases (Kinases P=4.7 × 10-4 in both algorithms respectively) and also Depression (P=4.2 × 10-2 in both respectively). These findings are supported by the high similarity between gene clusters generated by the Geodesic and Random Walk algorithms as shown in Table 3.
The Spectral Modularity algorithm also captures the important enrichment results found in both Geodesic and Random Walk algorithms. Enrichment for Kinase and Depression functional families can be found in community 5 (see Supplementary Table S4) for the Spectral Modularity algorithm, and correspondingly communities 4 in the Geodesic and Random Walk algorithms. As shown in Figure 2 this community encapsulates the well-studied MAPK/ERK signalling pathway [23]. There also exists a noticeable structural difference when clustering with the Spectral Modularity, compared to the Geodesic and Random Walk algorithms. The large community 3, observed in Figure 2a, was found to assimilate signals from various sources, including ionotropic and metabotropic signals from communities 1 and 2 [8]. This community, and the multiple signals it processes, separates as shown in Figure 2b into communities 3 and 4. With SH2 motif proteins (Src,Grb2) and PI3K/AKT pathway proteins (PI3-K,Akt2) bound to community 3, and Cytoskeletal and the well-studied Ser/Thr kinase Pka protein into community 4.
We further investigated the phenotype enrichment results with updated gene-disease annotation data collected from the OMIM [24], GeneRIF [25] and Ensembl variation [26] databases using the topOnto package, as shown in Supplementary Table S4. The annotation data was standardised using MetaMap [27] and NCBO Annotator [28,29] to recognise terms found in the Human Disease Ontology (HDO) [30]. Recognised disease ontology terms were then associated with gene identifiers and stored locally. Disease term enrichment, for a given dataset, could then be calculated using the Topology-based Elimination Fisher method [31] found in the topGO package (http:// topgo.bioinf.mpi-inf.mpg.de/), together with the standardised genedisease annotation data and the full HDO tree. As shown in Table 5, this approach allows us to compare the gene-disease association for the MASC dataset using the combined OMIM/GeneRIF/Ensembl variation data for common neurological and neurodevelopmental diseases and disorders: Schizophrenia, Alzheimer’s disease, Autistic disorder and Bipolar disorder. We further tested the enrichment results against a Neurological and Immunological clipped HDO tree following results found in [32], and a more stringent Neurological-specific tree, by clipping the full HDO tree for the “disease of mental health” and its children terms. From Table 5, we see the MASC dataset remains enriched for Schizophrenia and Alzheimer’s disease (P=1.5 × 10-9 and P=3.1 × 10-7) respectively. The following community enrichment values applied to the MASC network, use the combined OMIM/GeneRIF/ GeneRIF gene-disease annotation data and the neuro-specific ontology tree.
| MASC | Human PSD | BioPlex network | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Disease Name | N | HDO | Neural/Immune | Neural | N | HDO | Neural/Immune | Neural | N | HDO | Neural/Immune | Neural |
| Schizophrenia | 59 | 1.9 × 10-29 | 1.0 × 10-28 | 1.5 × 10-9 | 291 | 1.0 × 10-30 | 1.0 × 10-30 | 6.6 × 10-24 | 571 | 3.0 × 10-2 | 3.0 × 10-2 | 0.3 |
| Alzheimer’s | 19 | 1.2 × 10-23 | 5.1 × 10-23 | 3.1 × 10-7 | 196 | 1.3 × 10-23 | 2.2 × 10-22 | 2.7 × 10-5 | 537 | 3.6 × 10-7 | 3.7 × 10-7 | 1.3 × 10-5 |
| Autistic disorder | 25 | 5.6 × 10-7 | 8.8 × 10-7 | 3.7 × 10-2 | 62 | 1.1 × 10-5 | 2.0 × 10-5 | 0.27 | 158 | 0.84 | 0.84 | 0.96 |
| Bipolar disorder | 25 | 7.0 × 10-6 | 1.1 × 10-4 | 0.70 | 89 | 7.8 × 10-2 | 0.11 | 0.99 | 316 | 0.99 | 0.99 | 1.0 |
Top disease enrichment values for MASC [8], the human PSD [9] and BioPlex [17] datasets using combined OMIM/geneRIF/Ensembl variation annotation data (135782 gene-disease associations). Where enrichment values were calculated using the Topology-based Elimination Fisher method [31] and N gives the number of disease genes found in the dataset. First column in each section makes use of the full HDO ontology tree (6331 terms), the second the Neurological and Immunological clipped HDO tree (1118 terms) following [32], and the final a Neurological specific clipped HDO tree (243 terms) make use of the HDO:150 term and its children.
Table 5: Top disease enrichment values for MASC and the human PSD datasets.
Supplementary Table S4 shows that community 1 using the Geodesic, Random Walk and Spectral algorithms is enriched for Schizophrenia (P=5.5 × 10-3, P=1.4 × 10-3 and P=4.0 × 10-3 respectively). Evidence linking Alzheimer’s disease with crosstalk between the ERK/ MAPK and PI3K/AKT signalling pathways through activation of AKT proteins (Akt1) has been observed [33]. Using the Spectral algorithm, we find further evidence supporting this observation, with enrichment for Alzheimer’s disease (P=4.3 × 10-2) in the MAPK/ERK signalling pathway cluster, community 5 in Figure 2(b).
Typical community robustness values for the MASC network in our studies were found to range from 0.4 to 1.0, and from 0.26 to 1.0 for protein robustness. We used Cytoscape [7] to visualise the robustness information for the Geodesic (A), Random Walk (B) and Spectral Modularity (C) algorithms, as shown in Supplementary Figure S1. The robustness of each community is shown by the opacity of the community’s colour; the more opaque a community’s colour, the more confidence we have in it existing. The robustness of proteins inside the community is shown by the nodes size; bigger the node size, the more confidence we have in the protein existing within the community. In Supplementary Figure S1 we see the inter-connected nature of the enriched communities 1 and 2, and MAPK/ERK signalling pathway community 4 (community 5 for the Spectral Modularity algorithm). The large community 3 (communities 3 and 4 for the Spectral Modularity algorithm) is less robust. It is influenced by changes in the network structure, supporting its central role connecting communities in the network.
Human PSD network
Scalability of the suite’s performance to extract functional and disease enrichment was tested on the larger human PSD network. In a similar approach to that carried out on the MASC complex, we made use of the topOnto package to extract gene-disease annotation data from the OMIM, GeneRIF and Ensembl variation databases. The original study of the human PSD dataset was shown to exhibit a high density of neural disease enrichment [9]; reporting 269 diseases associated with 199 genes obtained using the OMIM database. A comparison of frequency of hits between the top 5 diseases in the original study and using the OMIM database with the topOnto package shows comparable results, see Supplementary Table S5. We extended the study to find enrichment for our diseases of interest in the PSD dataset, using the more populated OMIM/GeneRIF/Ensembl variation gene-disease annotation data and full HDO tree as shown in Table 5. We found the human PSD dataset significantly enriched for Schizophrenia and Alzheimer’s disease (P=1.0 × 10-30 and P=1.3 × 10-23 respectively), this remained true using the our clipped HDO ontology’s: P=6.6 × 10-24 and P=2.7 × 10-5 for Schizophrenia and Alzheimer’s disease respectively using the Neurological clipped tree.
For each algorithm we tested the disease enrichment per community for the top diseases shown in Table 5 (see Supplementary Table S6 for details). The community enrichment values for Schizophrenia, the most significantly enriched disease found in the human PSD network, are presented in Table 6. The P-values were calculated using eqn-5 and tested for their strength of significance. Table 4 compares the clustering performance on human PSD network using each algorithm. Where the Modularity values in Table 4 show evidence of greater clustering of the data using the Spectral Modularity algorithm (0.36), relative to the Geodesic (0.27) and Random Walk (0.18) algorithms.
| Geodesic | Random Walk | Spectral | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Cn | P-value | Sig (%) | C | Cn | P-value | Sig (%) | C | Cn | P-value | Sig (%) |
| 21 | 57 | 9.4 × 10-3 | 0.05 | 21 | 7 | 4.0 × 10-2 | 0.09 | 7 | 61 | 4.1 × 10-2 | 1.7 |
| 22 | 8 | 6.7 × 10-2 | 2.7 | 157 | 1 | 0.21 | 11.4 | 17 | 21 | 2.0 × 10-2 | 0.7 |
| 106 | 5 | 8.2 × 10-3 | 0.05 | 206 | 2 | 4.5 × 10-2 | 0.6 | 22 | 80 | 1.0 × 10-2 | 0.4 |
| 125 | 2 | 4.5 × 10-2 | 0.4 | 238 | 1 | 0.21 | 11.4 | 25 | 38 | 1.8 × 10-2 | 0.7 |
| 215 | 8 | 1.3 × 10-2 | 0.07 | 462 | 1 | 0.21 | 11.4 | 60 | 29 | 1.4 × 10-1 | 7.1 |
Top 5 communities for each algorithm in human PSD network enriched for Schizophrenia, based on the OMIM/geneRIF/Ensembl variation gene-disease annotation values from Table 5. Where Cn denotes community size and C the corresponding cluster number. P-value denotes the disease enrichment value for the cluster, and sig the percentage of P-values found, lower than or equal to the actual P-value, when 1000 random permutations of the disease labels were made.
Table 6: Community enrichment for Schizophrenia in the human PSD network.
Communities in Table 6, with size greater than 2, were further studied for possible enrichment of Schizophrenia related synaptic functional groups. Use was made of the 18 synaptic functional gene groups, covering 1026 pre- and post-synaptic genes, significantly associated with Schizophrenia [21]. It should be noted that the 18 functional gene groups are only used as classifications of functional type, and not group-truth clusters to test against. Three of the synaptic groups were found significantly associated with increased risk of Schizophrenia: Intracellular signal transduction (P=2.0 × 10-4), Excitability (P=9.0 × 10-4) and Cell Adhesion and Trans-synaptic (CAT) signalling (P=2.4 × 10-3). As shown in Table 7 (see also Supplementary Table S6), we found evidence supporting communities enriched for CAT signalling in each algorithm: community 106 (P=1.5 × 10-4) with the Geodesic algorithm, community 21 (P=1.3 × 10-2) with the Random Walk algorithm, community 25 (P=2.9 × 10-5) and community 17 (P=1.4 × 10-8) with the Spectral Modularity algorithm. The Spectral algorithm further supported enrichment of Intracellular signal transduction in community 14 (P=1.3 × 10-2), Structural plasticity in community 7 (P=2.8 × 10-5) and Protein cluster in community 22 (P=3.0 × 10-9). Community 22 shows postsynaptic adhesion molecules (including the DLG’s: DLG1/2/3/4) binding to specific presynaptic membrane proteins (CASK,LIN7A/B/C), providing evidence of a transynaptic link between the PSD and presynaptic active zone [34,35]. Our Spectral Modularity algorithm therefore (also the Geodesic algorithm through community 21 Table 7), captures tentative evidence for trans-synaptic signalling molecules involved in Schizophrenia clustered together solely driven by data.
| Geodesic | Random walk | Spectral | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Synaptic Function | Ng | N | C 21 | C 106 | C 215 | C 21 | C 7 | C 14 | C 17 | C 22 | C 60 |
| Intracellular signalling transduction | 150 | 86 | 7.4 × 10-2(2.2) | 1 | 9.2 × 10-2(2.4) | 1 | 0.5 | 1.3 × 10-2(0.4) | 1 | 0.1 | 1 |
| Neurotransmitter metabolism | 29 | 6 | 1 | 1 | 1 | 1 | 0.2 | 1 | 1 | 1 | 1 |
| Intracellular trafficking | 80 | 43 | 0.9 | 1 | 1 | 1 | 0.3 | 1 | 1 | 0.9 | 0.6 |
| LGIC signalling | 36 | 13 | 0.1 | 1 | 1 | 1 | 1 | 0.1 | 1.7 × 10-2(0.5) | 6.0 × 10-3(0.2) | 1 |
| Exocytosis | 26 | 37 | 7.3 × 10-2(2.3) | 1 | 1 | 1 | 0.8 | 1 | 1 | 1 | 1 |
| RPSFB | 71 | 50 | 1 | 1 | 1 | 1 | 1 | 1 | 0.6 | 1 | 0.7 |
| Ion balance/transport | 43 | 25 | 0.7 | 1 | 1 | 1 | 1 | 0.3 | 1 | 0.8 | 1 |
| Peptide/Neurotrophin signals | 28 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| G-proteins relay | 27 | 18 | 1 | 1 | 1 | 1 | 0.6 | 1 | 1 | 1 | 1 |
| ’Unknown’ | 61 | 25 | 1 | 1 | 1 | 1 | 0.7 | 0.3 | 1 | 0.2 | 1 |
| Excitability | 59 | 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 8.1 × 10-2(3.0) | 1 |
| CAT signalling | 81 | 34 | 0.2 | 1.5 × 10-4(0) | 1 | 1.3 × 10-2(0.2) | 1 | 1 | 1.4 × 10-8(0) | 0.6 | 1 |
| Endocytosis | 26 | 21 | 0.6 | 1 | 1 | 1 | 1 | 1 | 1 | 0.7 | 1 |
| Structural plasticity | 98 | 78 | 0.9 | 0.3 | 1 | 6.0 × 10-2(1.8) | 2.8 × 10-5(0) | 0.2 | 0.4 | 0.9 | 1 |
| GPCR signalling | 41 | 4 | 1 | 1 | 1 | 1 | 1 | 4.5 × 10-2(1.6) | 1 | 0.2 | 5.8 × 10-3(0.2) |
| Protein cluster | 47 | 35 | 3.4 × 10-10(0) | 1 | 1 | 1 | 1 | 1 | 1 | 3.0 × 10-9(0) | 1 |
| Tyrosine Kinase signalling | 7 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.2 | 1 |
| Cell metabolism | 57 | 36 | 1 | 1 | 1 | 1 | 0.8 | 1 | 1 | 1 | 0.6 |
The 18 synaptic functional gene groups associated with Schizophrenia [21]. This table shows the community enrichment and associated significance values, for community size (Cn) greater than 2, for each synaptic group, given in Table 7. Where N corresponds to the 522 functional genes (of the 1026 genes (Ng) assigned to groups in [21]) found in the network and C the corresponding cluster number. P-values the Bonferroni correction at the 0.05 significance level are also highlighted.
Table 7: Enrichment values for synaptic functional groups associated with Schizophrenia for the human PSD network.
Robustness of the communities found with the Spectral algorithm applied on the human PSD network was further investigated using our boot-strap procedure applied to the MASC complex. Typical values for community robustness range from 0.13 to 0.95 and from 0.04 to 0.98 for protein robustness as shown in Supplementary Figure S2. The robustness of each community is shown by the opacity of the community’s colour, while robustness of proteins inside the community is shown by the node’s size. Schizophrenia related genes are highlighted in magenta. Communities corresponding to those shown in Table 7 are highlighted along with the community robustness values. Edges have been made opaque to allow the networks clusters to be visualised.
Comparison with existing cluster algorithms
Enrichment results for the MASC and human PSD networks were also compared against popular Modularity based clustering algorithms available in R’s igraph package [10] and Cytoscape [11], shown in Supplementary Tables S4 and S6 respectfully. Algorithms tested include implementations of the agglomerative fast-greedy community algorithms (FC and GLay) [36,37], the agglomerative Random Walk algorithm (Walktrap) [38], the coupled Potts model and simulated annealing algorithm (SG) [39,40], the Markov clustering algorithm (MCL) [41], and implementation of the Spectral Modularity algorithm (LEC) [19] from R’s igraph package [10].
The parameters used in the FC, LEC, SG and Walktrap algorithms have been chosen to maximising the Modularity; further details of each algorithms parameter sets can be found in Supplementary Table S4 and S6. We used these algorithms with their optimised settings to test against the clustering results from our implementations. We find functional cluster similarities exist between each algorithm when applied to the smaller MASC network. However, when applied to the larger human PSD network, evidence for structurally relevant communities is restricted to the Spectral Modularity algorithm with fine-tuning step. Evidence for this is summarised in Section Human PSD network, Table 8 and shown in Figure 3. The Random Walk, Geodesic, Walktrap and MCL algorithms were found to generate skewed distributions of community size; one or two large communities with many single (or two gene) communities. The skewed distribution is a known cause of the hierarchical approach to clustering and the distribution of the hub (highest degree) nodes inside the network [42,43]. The FC, LEC, SG and GLay algorithms are observed to produce a small number of large communities. The agglomerative fastgreedy community algorithms, FC and GLay, are known to produce a small number of large communities [44,45]; the unbalanced nature of the algorithms merging step, results in a few large communities growing fast, by merging in many smaller communities. The SG and LEC algorithms are divisive in nature. Clustering results of the SG algorithm was found to be sensitive to the parameter gamma, which is set to 1.0 to maximise the Modularity. However increasing gamma to 5, which favouring more edges between communities than edges inside (lowering the Modularity score), we find the SG algorithm can also lead to improved functional enrichment results. We also note differences in the clustering results between our Spectral Modularity and the LEC algorithm.
| Algorithm | Source | Modularity (Q) | No: C | No: Cn=1 | No: Cn=2 | No: Cn>2 | No: Cn ≥ 100 | Largest Cn |
|---|---|---|---|---|---|---|---|---|
| Random Walk | Suite | 0.18 | 738 | 670 | 22 | 35 | 1 | 352 |
| Geodesic | Suite | 0.27 | 533 | 417 | 64 | 51 | 1 | 326 |
| Spectral | Suite | 0.36 | 60 | 14 | 5 | 41 | 1 | 146 |
| FC | igraph | 0.38 | 37 | 19 | 4 | 14 | 3 | 333 |
| LEC | igraph | 0.34 | 17 | 8 | 3 | 6 | 6 | 305 |
| SG (gamma 1) | igraph | 0.38 | 22 | 0 | 0 | 22 | 5 | 215 |
| SG (gamma 2) | igraph | 0.32 | 37 | 0 | 0 | 37 | 0 | 89 |
| SG (gamma 5) | igraph | 0.25 | 84 | 0 | 0 | 84 | 0 | 35 |
| Walktrap | Cytoscape | 0.30 | 242 | 166 | 19 | 56 | 3 | 301 |
| MCL | Cytoscape | - | 284 | 0 | 118 | 166 | 0 | 39 |
| GLay | Cytoscape | 0.65 | 31 | 11 | 7 | 13 | 3 | 387 |
The cluster characteristics for each algorithm applied to the human PSD network is given, including: the source of the algorithm, the maximum Modularity obtained (where possible), number of detected communities (C), the number of communities with size (Cn) equal to 1, the number of communities with Cn equal to 2, number of communities with Cn>2, the number of communities with Cn 100, and size of the largest community.
Table 8: Algorithm cluster characteristics applied to the human PSD network.
There are differences in implementation between the two Spectral Modularity algorithms. We provide here a descriptive and quantitative account for why, in our opinion, our Spectral Modularity implementation delivers functionally more relevant clusters when applied to the proteomic datasets. We do not claim to cover all differences here. Both implementations use the same divisive hierarchical method to clustering data [19]. We therefore tested whether our fine-tuning step gave closer agreement to the LEC results or not. If the two implementations were identical, with the fine-tuning step in operation or not, we would expect a NMI value of 1. We note we reproduced the Modularity values quoted in [19] for the Zachary’s ``karate club’’ network, with and without the fine-tuning step (see Supplementary Table S6). We further find agreement with the LEC algorithm results with our fine-tuning step switched off (NMI value of 0.72 compared to 0.31, see Supplementary Table S6) when applied to the human PSD network. This would suggest it is the addition of a fine-tuning step, which has a positive effect on the clustering of proteomic data and quality of functional clustering results, as highlighted in Section Human PSD network and Supplementary Tables 7 and 8. Differences in speed between the two implementations can be explained in the different eigenvector solver used. We make use of Numerical Recipes [46], which computes the full eigenvalue spectrum. The LEC implementation makes use of ARPACK [47], which calculates only a few of the leading eigenvalues, and is commonly found to perform faster than Numerical Recipes (Performance of ARPACK, Eigen, and Numerical Recipes, https://github.com/meznom/arpaca/tree/ performance/).
BioPlex network
To test how our findings translate to other large proteome datasets we looked at the BioPlex network [17]. This network is made from data obtained from a large-scale proteomic analysis of 2594 affinity purified baits that identify 7668 proteins from HEK cells. Therefore, we used a similar approach to that carried out on the MASC complex and human PSD network and extracted gene-disease annotation data for the BioPlex network as shown in Table 5 (see also Supplementary Table S8) and tested for enrichment. Unexpectedly we found evidence that the BioPlex network is enriched for proteins implicated for Alzheimer’s disease (P=3.7 × 10-7), this remained true using our Neurological and Immunological clipped HDO tree (P=3.7 × 10-7) and Neurological clipped tree (P=1.3 × 10-5). We note that this result supports in part a possible neuronal origin of the HEK293 cell line [48,49].
The clustering performance of our Spectral Modularity algorithm was tested against the clustering found in the BioPlex study [17]. The BioPlex network was first clustered using clique percolation, before further sub-divided using the fast-greedy community algorithm into 345 communities. A priori we would not expect similarity between the clique-based BioPlex clustering and our Modularity-based Spectral algorithm, as both starts from different definition of what a community is. However, if we compare the BioPlex clustering to our Spectral Modularity algorithm as shown in Table 9, we find our Spectral Modularity algorithm shows evidence for cluster similarities (NMI 0.7 and ARI 0.38) with those found in the BioPlex study. The coupled Potts model and simulated annealing algorithm (SG) [39,40] also shows evidence for cluster similarity, but as we discuss in Section Comparison with existing cluster algorithms this algorithm is sensitive to tuning its parameter gamma.
| Algorithm | Modularity (Q) | No: Communities | CPU-time | NMI | ARI |
|---|---|---|---|---|---|
| BioPlex | - | 354 | - | 1.0 | 1.0 |
| Spectral | 0.56 | 250 | 253.0 | 0.7 | 0.38 |
| FC | 0.6 | 61 | 0.025 | 0.47 | 0.12 |
| SG1 | 0.63 | 64 | 75.0 | 0.63 | 0.25 |
| GLay | 0.77 | 60 | - | 0.47 | 0.12 |
Maximum Modularity (Q), number of detected communities (C) and sequential CPU time (in minutes) for the Spectral Modularity, FC, SG1 and GLay algorithms (as discussed in Table 2) applied to the BioPle × network in Table 1. The Normalised Mutual Information (NMI) and Adjusted Rand Index (ARI) metrics for each algorithm relative to the clustered BioPlex network is given.
Table 9: Algorithm characteristics applied to BioPlex network.
We further tested the communities found using our Spectral Modularity algorithm, and those in the BioPlex study, for enrichment of our diseases of interest (see Supplementary Table S8). As shown in Table 10, we found evidence supporting communities statistically enriched for Alzheimer’s disease using our Spectral Modularity algorithm. It was noted that by clustering the BioPlex network using the Spectral Modularity algorithm, we started to reach the known Modularity resolution limit [50]. However, we found many (110) of the BioPlex communities (greater than 2 in size) contained within our own, and by re-running our Spectral Modularity algorithm over these communities, could recover the sub-structure contained within them, including core components of the original BioPlex clusters. An example of this is shown in Supplementary Table S8, where BioPlex’s cluster 12 has been extracted from within our original community 6.
| Spectral | BioPle × | ||||||
|---|---|---|---|---|---|---|---|
| C | Cn | P-value | Sig (%) | C | Cn | P-value | Sig (%) |
| 11 | 37 | 4.1 × 10-2 | 1.6 | 4 | 22 | 0.12 | 11.0 |
| 34 | 38 | 4.1 × 10-3 | 2.7 | 8 | 17 | 6.6 × 10-2 | 10.4 |
| 58 | 132 | 2.0 × 10-2 | 0.05 | 9 | 51 | 0.32 | 13.3 |
| 82 | 3 | 1.4 × 10-2 | 0.4 | 18 | 13 | 0.16 | 11.4 |
| 237 | 63 | 7.0 × 10-2 | 0.07 | 51 | 5 | 1.6 × 10-3 | 9.8 |
Top 5 communities enriched for Alzheimer’s disease using the Spectral Modularity and BioPlex clustering algorithms, based on the OMIM/geneRIF/Ensembl variation gene-disease annotation values from Table 5, where Cn denotes community size and C the corresponding cluster number. P-value denotes the disease enrichment value for the cluster, and sig the percentage of P-values found, lower than or equal to the actual P-value, when 1000 random permutations of the disease labels were made
Table 10: Community enrichment for Alzheimer’s disease in the BioPlex network.
We present a suite of C++ implemented Modularity based community detection algorithms. The implementations have been optimised for speed using OpenMP and tested on varying sizes of synthetic networks. The suite is designed to run on clusters and includes a boot-strap facility, allowing a random sub-sample of the data to be selected; currently set to 80% of the network node size. Sampling from multiple bootstrap runs allows the robustness of each algorithm applied to the data to be investigated. The package clusterCons [20] has been used in conjunction with the suite, to build a consensus matrix from which to test the robustness of discovered communities, and proteins found inside each community. The package topOnto has been used in conjunction with this suite, to study the disease enrichment values of clusters obtained from published studies. We find our Spectral Modularity algorithm out performs the Geodesic and Random Walk edge Betweenness algorithms in terms of speed as shown in Table 2. It also out performs commonly available clustering algorithms in unveiling functional enrichment in proteomic datasets, as shown in Table 8 and in Supplementary Tables S4 to S6. Further investigation reveals the fine-tuning step, in conjunction with the Spectral Modularity method, is of key importance.
The datasets supporting the results of the article are included within the article (and its additional files). A C++ version of the suite is available to download at SourceForge following: http://sourceforge.net/projects/ cdmsuite/. The C++ version requires a standard gcc compiler; we tested against version 4.4.7, and has no external dependencies. A Cytoscape App for the Spectral Modularity method is also available. The App requires Cytoscape version 3.0.0 or higher, and was tested against version 3.2.1.
None declared
Implementing OpenMP versions of Geodesic and Random Walk edge Betweenness algorithms. Implementation of Spectral Modularity algorithm.
We wish to thank Theologos Kotsos, Oksana Sorokina, Andrew Pocklington, Giuseppe Gallone and Vathsala Achar with help in testing these algorithms and with general discussions.
The research leading to these results received funding from the European Union Seventh Framework Programme under grant agreement nos. HEALTH-F2-2009-241498 (“EUROSPIN”), HEALTH-F2-2009-242167 (“SynSys”), and European FET flagship project “Human Brain Project” (Subproject 1, Strategic Human Brain Data, WP1.3: T1.3.1 and T1.3.2).