Sociophysics [1] in the early nineteenth century and biophysics [2] in the early twentieth century, were attempts to formalize the social and life sciences, respectively, using computational techniques from physics. A major difficulty encountered was modeling the complexity of even the most familiar phenomena outside the physical sciences. Unlike linear phenomena, which have a spectral decomposition and are therefore tractible, complex phenomena have large numbers of entangled components that typically cannot be decomposed into fundamental modes. As pointed out in Ref. [3] complexity is a delicate balance between regularity and randomness; the stability and adaptability of a complex process can be lost through an imbalance favoring one over the other. Consequently, extending the early modeling of physical phenomena to the behavior of living organisms, either individually or collectively, was almost uniformly disappointing.

The initial successes of physics modeling relied in large part on Newton’s concept of a mechanical force, which seemed to have no direct correspondent in social sciences, except in a metaphorical sense, and to be of only selective utility in the life sciences. The lack of a physical force in these latter sciences is not surprising, given that the dynamical variables indigenous to their study are not physical in nature. Consequently, the genesis of a non-physical force, if there is one, must be traced to a non-physical source.

Physics has historically involved a search for the most parsimonious description of Nature’s behavior and as a science it has been wildly successful in doing this, when it comes to describing the dynamics of the inanimate. Consider, the empirical notion of energy conservation, which implies that energy can neither be created nor destroyed; it can only change its form, switching back and forth between potential and kinetic. An energy gradient in a conservative physical system defines a mechanical force. When a physical system becomes complex its natural description is given by thermodynamics, which introduces a nonmechanical physical force; the entropic force. This latter force involves the gradient of the entropy

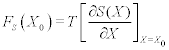
where T is the temperature, X is the macroscopic state variable, with X₀ the present state, and SX₀ is the system entropy. An example of a physical process driven by an entropic force is osmosis. The entropy gradient is herein replaced with an information gradient in non-physical systems, or by a complexity gradient if you prefer, to define a non-mechanical force. This is an information force and is a consequence of the mismatch in complexity of two interacting systems, as we demonstrate.

The mathematician who initiated the science of the man-machine interface, Norbert Wiener, speculated that the complex networks within the social and life sciences behave differently from, but not in contradiction to, those in the physical sciences, with control emanating from the flow of information, not the flow of energy [4]. He conjectured that a system high in energy coupled to one low in energy, but extremely high in information, can be coupled such that the information, which he, following Schrödinger [5], referred to as negative entropy, passes from the system at low energy to the system at high energy and subsequently determines the organization of the latter, cf. Figure 1. The significance of his conjecture cannot be overstated. Wiener’s speculation implied that the force laws and control in social phenomena do not follow the negative gradients of energy potentials (even if they could be defined), but rather they follow gradients produced by information imbalance. We refer to this as Wiener’s Rule (WR) (Figure 2).

Figure 1: Cross-Correlation Cube.

Figure 2: Wiener’s Rule.

fthFU4.8427in3.2461in0pt Wiener’s Rule: The upper panel denotes the familiar thermodynamic situation of an energy-dominated interaction. The lower panel depicts the counter-intuitive information dominated interaction. Adopted from Ref. [6] (Figure 2) wienerwiener rule.tiflanguage “Scientific Word”;type “GRAPHIC”;maintain-aspectratio TRUE;display “USEDEF”;valid_file “F”;width 4.8427in;height 3.2461in;depth 0pt;original-width 6.093in;original-height 4.073in;cropleft “0”;croptop “1”;cropright “1”;cropbottom “0”;filename ’Wiener Rule.tif’;file-properties “XNPEU”;

The thermodynamic concept of entropy has recently been applied in a biological context by Demetrius et al. [7] to explain Darwinian evolution. They introduced ‘evolutionary entropy’ to provide a context in which allometry relations, between body size and metabolic rate, as well as, body size and maximal life span, can be predicted. This is one of the more recent contributions in an ongoing strategy to offer an alternative to energy as the fundamental tool for the understanding of complexity, order and organization in biosystems. In 1953 one of the first meetings was held to explore the importance of entropy to quantify the information content in a living system [8], from macroscopic biodynamics down to protein structure. Some three decades later, entropy was offered as a unifying principle for biological evolution by Brooks and Wiley [9]. Similar attempts have been made to explain social organizations using theories of social entropy [10,11]. All these efforts and many more went unaware of Wiener’s contribution to the discussion.

WR remained speculation for over sixty years. It was only with the recent activity to develop a science of networks that an extension of this rule was established. The proof relies on generalizing some of the fundamental ideas of non-equilibrium statistical physics, in particular linear response theory (LRT) to non-stationary phenomena [12,13]. The science of thermodynamics explains the movement of heat and other irreversible phenomena in the physical world and statistical physics seeks to explain the thermodynamic formalism, using the microscopic dynamics of physical systems. The network dynamics of a person or of a group of individuals are very different, however.

As the networks in which we are immersed become increasingly complex, a number of apparently universal properties begin to emerge. One of those properties is a generalized version of WR having to do with how complex networks, perhaps involving phenomena from very different scientific disciplines, exchange information with one another; this is described by the Principle of Complexity Management (PCM). The efficiency of the information transfer is dependent on the relative complexity of the two networks, and the complexity gradient gives rise to a complexity-induced information force.

On a larger stage Karl Marx [14] talked about class conflict as the driver of social evolution, whereas Adam Smith [15] invoked an invisible hand to visualize the unintended social benefit resulting from individual actions of self-interest and Freud [16] argued for instinct, as the primary cause of human behavior. At both the level of the individual and the collective these exemplify what could be included under the general heading of information forces; non-physical forces resulting from gradients in the complexity of the phenomena being studied.

We adopt the probability density as the measure of the information content of a network in keeping with the determination of the negative entropy adopted by Wiener [17] and Shannon [18]. More specifically, we use the inverse power-law index as the statistical measure of complexity. The inverse power-law distribution is taken to be the signature of complexity by most, if not all, network scientists and is the asymptotic form of the hyperbolic survival probability:

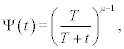(1)

Where t is the time interval between events. Examples of phenomena represented by such a survival probability include the time interval between: breaths and heart beats, emails, and earthquakes of a given magnitude, see e.g., Ref. [3] for a more extensive list of phenomena. The average time between events can be determined using the probability density

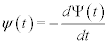(2)

such that

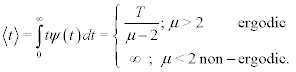(3)

It is interesting that when the power-law index is in the interval 2<μ<3 the distribution has a finite first moment and the network’s time series has ergodic statistics, subsequently we call this an ergodic network. In the situation μ<2, however, there are no finite integer moments and the ensemble and time averages are not necessarily equal; the statistics are non-ergodic. Consequently, we have a nonergodic network. In either case the generalized linear response theory (GLRT) [13] yields:

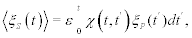(4)

Where x(t,t′) is the generalized linear response function (GLRF) given by [12,13]:

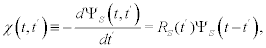(5)

and R_S(t) is the rate at which events are produced by a network S prepared to have an event at t=0, i.e., the bits per second encoded in ξ_S(t). Here <ξ_S(t)> denotes the Gibbs ensemble average over infinitely many responses of ξ_S(t) to ξ_p(t). The variable ξ_p(t) is the time-dependent stimulus generated by the network P and ε<<1 is the stimulus strength.

For simplicity we take both signals ξ_S(t) and ξ_P(t) to be dichotomous and fluctuating between values ± 1. The time intervals between two consecutive crucial events is referred to as laminar regions. It is important to remark that Equation (4), for the response of the network S to the perturbing network P, is valid when the network is prepared at time t=0 and placed at the beginning of a laminar phase, and the interaction with the perturbation P is turned on at the same time. The network P exerts its influence on S as follows: if S has an event at time t and if its next laminar region will be assigned a value with the same sign of the value of ξ_P(t), then S is perturbed so that its next laminar region will tend to be longer, by assigning to its parameter T in Equation (3) the value T+=T(1+ε). On the contrary, if the next laminar region of S will have a value with the opposite sign of ξ_P(t), then the value T-=T(1-ε) will be used, thus tending to make the next laminar region shorter.

The cross-correlation function measures the transfer of information between the two complex networks. It can be constructed by inserting Equation (5) into Equation (4), multiplying the resulting expression by ξ_P(t) and averaging over an ensemble of realizations of ξ_P(t) to obtain:

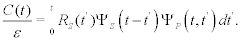(6)

The stimulating network is characterized by the non-stationary autocorrelation function p(t-t′), which depends separately on the time of the last perturbation t′ and the time of the measurement t. Equation (6) is the basis for the cube depicted in Figure 1.

In the context of one complex network stimulating another, e.g., the transportation system and the brain, it is possible to prove that the response of the brain to the noise fades as an inverse power law :

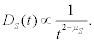(7)

The response to the stimulus fades to zero and asymptotically approaches region II of the cube. This non-ergodic condition of the brain is asymptotically unresponsive to ergodic and/or periodic stimuli: the complexity of the neural network essentially swallows up simple signals through its complex dynamic interactions. But even when the brain is in the ergodic regime 2<μ_S<3 its response decays to a constant value determined by

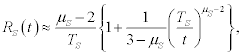(8)

which is less than the full response of region III in Figure 1, but it does not vanish altogether.

fthFU4.8526in4.1137in0pt The cross-correlation (magic) cube: The asymptotic cross-correlation function is graphed as a function of the two power-law indices of the stimulating network P and the responding network S for infinite time. The cube graphically displays the properties of the Principle of Complexity Management. The figure is adapted from [13]. Figure 1 cubecube.tiflanguage “Scientific Word”;type “GRAPHIC”;maintain-aspect-ratio TRUE;display “USEDEF”;valid_ file “F”;width 4.8526in;height 4.1137in;depth 0pt;original-width 2.8717in;original-height 2.4317in;cropleft “0”;croptop “1”;cropright “1”;cropbottom “0”;filename ’cube.tif’;file-properties “XNPEU”;

The complexity of networks is herein quantified, as previously mentioned, by inverse power-law distributions and consequently by their power-law indices. These inverse power laws are a consequence of the often non-stationary and non-ergodic fluctuations, generated by nonlinear dynamics. Such temporal complexity has been shown to be a consequence of criticality, resulting from network dynamics [19] and was used to determine the efficiency of information transfer between two interacting complex networks. However, because of the ubiquity of such inverse power-law networks [20] the imposed restriction is not overly severe and so we need not restrict our remarks to a specific network model. We consider two temporally complex networks exchanging information, for example, two people taking turns talking to one another [21], or the excitation of the human brain engaged in simple tasks such as finger tapping in response to stimuli [22]. Each complex network considered here has its own characteristic exponent that is a consequence of its dynamics and not its topology. The efficiency of the information transfer between two such networks is determined by the relative values of their complexity indices [20].

One measure of the information transfer between two complex networks is the cross-correlation of the output of a complex network P with that of a complex network S, being stimulated by P. The dynamics of the responding time series is represented by a dichotomous time series ξ_S(t) as is that of the stimulating time series by ξ_P(t). Both time series have inverse power-law distributions of time intervals between events, an event being a switch between values. The time series is ergodic when the time average and ensemble average are equal, which occurs when the power-law index μ, with an appropriate subscript, is in the interval 2<μ<3. The time series is non-ergodic, the two averages are not equal, when the power-law index is in the interval 1<μ<2, and the average time between events diverges, see Equation (3). Consequently, there is no characteristic time scale for a non-ergodic process. Note that most of non-equilibrium statistical physics literature assumes the dynamics of the systems of interest to be ergodic. But what happens to the information transfer when one network is ergodic and the other is not?

The simplest measure of the lasting influence of network P on network S is given by the asymptotic cross-correlation function. In Figure 1 the asymptotic cross-correlation function, normalized to one, is graphed as a function of the power-law indices of the two networks to form the cross-correlation cube. This cube displays a number of remarkable properties:

1) The upper plateau, region III, indicates that when P is non-ergodic, 1<μ_P<2, and S is ergodic, 2<μ_S<3, the time intervals between stimulating P-events can be very long and the time intervals between unperturbed S-events are much shorter, on average. Consequently, more S-events occur in response to the P-events than would occur naturally and therefore the greater information in the P network dominates the process, producing complete correlation, between stimulus and response. An example of the kind of physical process captured by this region of the cube is a leaky faucet (P network) keeping a person (S network) awake at night, see Section 4.

2) The lower plateau, region II, indicates that when P is ergodic, 2<μ_P<3, and S is non-ergodic, 1<μ_S<2, the time intervals between S-events are much longer than those of the P-event stimuli, on average. Consequently, the sporadic disruptions of S-events are not detectable asymptotically. The information-rich S network washes out the influence of the stimulus. An example of the kind of physical process captured by this region of the cube is the sound of traffic (P network) that fades from consciousness as a person (S network) falls asleep, see Section 4.

3) When the power-law indices are both equal to two, there is an abrupt jump between region II, with no correlation, and region III, with perfect correlation, at the center of the cube; the spectrum associated with this exchange is exactly 1/f. This matching of complexity, between two interacting complex networks, may well be the origin of the ubiquity of the mythic 1/f-noise [3], see Section 4.

It is noteworthy that property-1 captures WR and shows that a network with the greater information can organize and control one with lesser information, essentially independently of the relative energy content. It should also be emphasized that property-2 describes the well-known psycho-physical phenomenon of habituation [23]. As humans we respond to a strong stimulus, but if the stimulus remains unwavering, such as a pungent odor in a deli, or random traffic noise, then after a relatively short time the response fades; we no longer smell the strong odor or hear the drone of a monotonous speaker. Finally, and perhaps most importantly, we have the ubiquitous phenomena of 1/f-noise described in property-3. This property has been determined to result from the interaction at the interface of the two complex networks being in a kind of statistical resonance [3].

The Principle of Complexity Management (PCM), embodied in the cube [12,13], indicates how one complex network responds to stimulation from a second complex network as a consequence of the relative information content of the two networks. WR described the influence of the stimulus as it appears on the upper plateau region of the cube, where the information in the stimulus exceeds that in the response. In all regions, except the lowest one, the weak stimulus significantly modifies the properties of the responding network. In the upper plateau, region III, the stimulus actually dominates the properties of the response and reorganizes it, just as Wiener predicted it would. However, WR is now part of the more general PCM, which quantifies WR by introducing a measure of information in complex networks that enables comparison of the level of information in interacting networks. This measure is the power-law index of the distribution, which in combination with GLRT, enable the construction of the cube to determine the degree of asymptotic influence one network exerts on the other, see Section 2. Thus, the veracity of the speculative WR has been established mathematically [13], as well as, its extension to the entire domain captured in Figure 2.

The various quadrants of the cross-correlation cube are related to the habituation phenomenon, in one form or another. Habituation is a primitive form of learning, through which humans and other animals learn to disregard stimuli that are no longer novel, thereby allowing them to attend to new stimuli [23]. A repeating stimulus of unvarying amplitude and frequency content induces a response that fades over time, since no new information is being presented to the animal. The lack of new information allows the brain to shift its focus from the more to the less familiar, the latter providing new information that may have survival value. However, we know that the brain does not habituate to all external stimuli, so we consider two distinct forms of stimulation: one ergodic 2<μ_P<3 and another non-ergodic 1<μ_P<2. Consider highway noise coming in through the window of your motel room as you lay in bed. This noise is typically a broad band, uncorrelated random process and consequently it is ergodic. Most people habituate to this noise, meaning that the brain’s neurons no longer fire in response to this excitation and they soon fall asleep. The rate of decay to region II of the cube is given by Equation (7).

The next stimulus we consider is the sound of water dripping from a faucet and splashing in the basin below. Unlike the traffic noise that can lull one to sleep, the sequence of crashes from the drops of water striking what sounds like a drum head, often induces insomnia. Experiments have determined that the distribution of time intervals between water droplets is Lévy stable, which asymptotically becomes an inverse power law with index μ_P ≈ 1.73 [24,25]. The precise value of the index depends on the conditions of the experiment, but typically the index falls in the domain 1<μ_P<2. Over the interval 1<μ_S<2 the brain response increases linearly with increasing μ_S, until it reaches the upper plateau. Over the interval 2<μ_S<3 the asymptotic brain response to the intermittent splashes given by the cross-correlation function is uniformly maximum. The upper plateau depicts the parameter domain where the brain is ergodic and tracks the sound of every intermittent drop of water and being unable to predict, even approximately, when the next splash will occur, the general response is annoyance and wakefulness.

Property-3 focused on the precipitous drop from the upper to the lower plateau regions in the center of the cube. The striking difference between the response to a simple (ergodic) stimulus and the response to a complex (non-ergodic) stimulus is intimately related to the emergence of 1/f-noise. We have shown elsewhere [13] that the spectrum of the P-network is 1/f^3-μP, where f is the frequency of the spectral component of the non-ergodic stimulus. Only at the crucial condition μ_P=2 does the ideal case of 1/f-noise occur, where the maximal information transmission rate is achieved.

These results strongly suggest that, just as physical forces are the consequence of the variation of energy, so too “ information forces” are the consequence of the variation of information or equivalently of complexity. In a strictly physical and in some biological systems, these two types of forces coalesce into the entropic force, such as observed in the elasticity of a freely-jointed polymer molecule [26], in entropic crystals [27] and the force between biological membranes [28]. However, in the social and psychological realms, the force results from the structure and stochastic nature of the complexity associated with a network’s information content and therefore it might be viewed as an information force, rather than an entropic force.

The existence of an information force is a new concept requiring significant research to determine if it is merely a metaphor, based on the identification of entropy with information, as originally made by Maxwell [29], or whether it is a viable source for controlling, as well as understanding, organization in non-physical systems. The crosscorrelation cube suggests the existence of this phenomenological force as a consequence of the PCM; a force resulting from the statistical tendency of a complex network to decrease its information content, as distinct from a force arising from a specific energy gradient.

The excellent review of thermodynamics and information [29] lays out the arguments for information being physical, in the same way that entropy is physical. The use of Maxwell’s demon in the argument almost certainly restricts the information being considered to physical processes. The only scientific discipline brought into their discussion from outside the physical sciences was biology, where the interleaving with physics was quite clear. Consequently, the argument for the physicality of information is still not obvious in the myriad of applications of information to phenomena in psychology and sociology. It is probably this distinction that Shannon had in mind when he stipulated that his use of entropy as the measure of information would not include the meaning of the message being communicated, since meaning could not be quantified.

When a person says they are “being forced to do something”, it is usually not a physical force that is being applied to illicit that response, although an image invoking that metaphor may come to mind. What is meant is that another person or organization, with greater information concerning their future well being, is determining that they do something, which, left to their own devices, they would not do. And, of course, in order for this force to be effective they must have the person’s consent. Recall the experiments of Milgrim [29] on a person’s blind obedience to authority.

I wish to thank M. Turalska for her perceptive remarks concerning earlier versions of the paper and her insights regarding information sharing in general.