A sizeable proportion of the forests in the European Union (EU) is in private hands [1], and private forest ownership is increasing in the forest-rich sub-regions of Central-East and Northern Europe [2]. Thus, considering the attitudes and objectives of private forest owners is important for ensuring that policy instruments are effective [3]. It is also important to recognize that forest owners are far from a homogeneous group as regards objectives and attitudes (see, e.g., [4-8]).

Hence, efficient policy impact analysis requires the ability to model the interaction between policy and forest management decisions, also acknowledging the heterogeneity of forest owners. Ex_isting Decision Support Systems (DSS) operational at pan-European level are somewhat lacking in this respect. In the instances where forest owner heterogeneity is accounted for, simplistic heuristic approaches are used. An example is the EUwood study (Hamburg University 2010) where forest owner harvesting behavior was linked to forest holding size, so that small forest holdings were assumed to result in a smaller percentage of the theoretical wood supply being available. Another prominent example is the EFSOS II study [9] (UNECE/FAO), which provided so called policy scenarios—dep_icting the outcome for the European forest sector when the priority of forest management is given to different objectives—for the assessment of trade-offs facing policymakers. Just as was the case in the EUwood study, the pan-European forest resource assessment model EFISCEN [10] was used both to provide estimates of potential wood supply, in EFSOS II ingested as a constraint on the production of wood products in the economic forest sector model EFI-GTM [11], and to project the future state of the forests given assumptions of future wood demand and pre-specified management regimes.

The analysis in these two studies neither considered the reaction of forest owners to policy and the effect of forest owner heterogeneity on the inter-temporal development of forests, nor the logical feedback ex_isting from the forest sector model to the forest resource assessment model. The latter constitutes a relevant problem, since multiple errors would propagate over time if the ‘actual’ quantity of harvested wood were set equal to this upper bound, without taking into account that the satisfaction of the demand might have required a lower harvesting level. Hence, this kind of modelling endeavors has its value for response analysis, but is not very useful for policy impact assessment or forecasting.

Further, information is a commonly used policy instrument, not the least in the context of forest policy [12]. The importance of information as a policy tool is illustrated by considerable efforts spent by Member states of the EU on information, training and capacity building of private forest owners to foster wood mobilisation (Standing Forestry Committee ad hoc Working Group II 2008). Information as a policy tool certainly works by modifying the expectations of forests owners/managers about the future, e.g., concerning demand and prices, so that informed harvesting decisions are taken using updated expectations [13]. Consequently, policy impact analysis presupposes the ability to model the reaction of forest owners to policy in the form of information releases.

Thus, the current study aims to provide a theoretically founded framework to incorporate forest owner heterogeneity, including the asymmetric response to information, in a DSS. Departing from earlier studies using the Fisherian two-period consumption-saving-harvesting model [14-20], in particular Rinaldi and Jonsson [13], we develop a theoretical model of harvesting behavior when forest owners differ as to the receptiveness to information. This theoretical model is then used as the basis for a more complex simulation tool—Expected Value Asymmetries (EVA)—allowing for a higher degree of heterogeneity in terms of forest owners’ preferences. EVA is subsequently used to demonstrate how forest owner heterogeneity affects both the intertemporal development of forests and timber market conditions. Further, it is discussed how EVA, by working as an intermediary, could provide feedback from an economic forest sector model to a forest resource assessment model, while at the same time ensuring that forest owner specific harvesting behavior is integrated in the DSS.

The paper proceeds as follows: the next section presents the theoretical model, with particular emphasis on the modelling of uncertainty and information arrival. Then the policy simulation tool EVA is presented. Hereafter, simulation results are presented and discussed. The subsequent section outlines how EVA could be part of a DSS, completing the feedback loop between an economic model of the forest sector and a forest resource assessment model while at the same time ensuring that forest owner harvesting behavior is accounted for. The paper concludes with summary and conclusions.

The theoretical model used here is simple and stylized. First of all, in order to derive analytical solutions, we consider a two-period economy, so that the optimal harvesting problem of each forest owner reduces to how much should be harvested immediately and how much in a(n) (indeterminate) future period. Further, for what concerns policy making, we simply assume that some unspecified policy is initiated at the beginning of period one, and forest owners perceive it as new information (i.e., a signal) regarding timber demand and prices. Policy design is obviously an issue of considerable importance. However, it is beyond the scope of this paper, whose focus specifically is the modelling of forest owners’ harvesting behavior.

The representation of policy through signals is particularly interesting, allowing the policy to be perceived as “good (news)” or “bad (news)” from the forest owner perspective. Further, it accounts for the circumstance that policy-effects might be perceived as long lasting and/or time contingent, and also for the specific degree of confidence of individual forest owners/managers (in the policy maker). The theoretical model exclusively focuses on direct economic risk (as opposed to biological risk), a choice that is at least partially supported by empirical evidence showing that private forest owners consider direct economic risk, such as price changes, much more important than indirect economic risk resulting from biological damage [21].

We consider a two-period economy in which two distinct groups, I and NI, of risk-averse private landowners want to max_imize the utility derived from individual final wealth, by choosing how much to harvest in each period. Within each group landowners are identical, further we also assume that they all have the same utility index U, with exponential form and constant risk-aversion r, that is U=-exp(-rw^j), where w^j represents wealth at time 2 for an individual belonging to group j=I, NI. Besides having identical preferences, all the forest owners are also initially endowed by identical forests characterized by the same area, age, tree species and growth function.

Each landowner harvests in both periods, in particular, we denote by x^j _i the quantity harvested at time i by a generic landowner belonging to group j. Given the amount harvested at time 1, x^j ₁, the stock available at time 2 is uniquely defined by the growth function and the initial forest endowment Q. In addition, since we are assuming that utility derives from final wealth only, and that the rotations beyond the second period are ignored, it also follows that such a stock will be entirely harvested at time 2. For simplicity we will consider a linear growth function. Obviously such an assumption violates the concavity requirement, however, our analysis does not crucially rely on this specification, which instead allows for a reduction in the notational and computational complex_ity of the model. Therefore, we assume:

x^j2=k(Q-x^j₁) 0≤x^j₁≤Q (1)

where Q is the initial forest stock, and k a positive constant.1

The demands for wood in both period, D₁ and D₂, are inelastic and unknown. We let p_i be the price at which wood harvested at time i is sold on the wood market. Notice that, since the forest must be harvested completely at the end of the second period, and since demand is inelastic, our framework focuses only on the realization of the time 1 equilibrium through the equilibrium price p₁. Finally we assume that timber revenues p₁x^j₁ are invested at time 1 on a risk free bond with gross return (1+ b), at time 2.

When the landowner makes his/her harvesting decision, the demand D₁ and the timber prices are not known. However, all landowners know that p₁ is derived as an equilibrium price, while they hold beliefs concerning the distributions of D₁ and the dynamic of prices. In particular, both D₁ and p₂ are driven by a stochastic common component ε_a that can be thought of as a long-run economic shock affecting both periods (an example could, e.g., be a realization of the bioeconomy, creating a long-term increase in the demand for wood), and two time contingent shocks, ε_D and ε₂, respectively. The variance of ε_a, σ_a²;, can be thought of as a measure of economic risk. The two shocks ε_D and ε₂ are mutually independent, and, in addition, they are also independent from ε_a. Therefore, they represent specific time contingent shocks exclusively affecting time 1 (ε_D), and time 2 (ε₂), respectively. Hence, σ_D² and σ₂² can be thought of as measures of time specific risk. To make examples, one can imagine a temporary variation in exchanges rates affecting timber demands, or a provisional reduction in the activity of a major sawmill in the area in question.

Hence, D₁=D(1+ε_a)+ ε_D and p₂=p₁(1+m)+ε_a+ε₂, where m, D∈ℜ??, ε_a ∼N(0, σ_a²), ε_D ∼N(0, σ_D²), ε₂ ∼N(0, σ₂²). The constant D can be thought of as base demand level, and the percentage variation from it (ε_a) depends on the overall long-run economic development. In addition, the forest sector (and henceforth the demand) can be hit also by a timecontingent shock ε_D, which will have no residual effect at time 2. The price at time 2, depends on the equilibrium price at time 1, the long-run economic shock, ε_a, and the time specific shock for time 2, ε₂. Notice that, since the forest will be harvested at the end of the second period, only the demand in the first period is relevant for the analysis.

For concreteness, we assume that m>b, for example one can imagine that m is a fixed inflation rate and, in absence of any additional information, forest owners/managers might assume that future timber prices will adjust for inflation

The model assumes that while uncertainty definitely resolves at time 2, with the realization of the timber price, p², some news concerning the forest sector already arrives at the beginning of time 1, through a signal s. In particular,

s=αε_a+ ε_D+ε_s (2)

where ε_s is a noise distributed according to ε_s∼N(0, σ_s²). Only the members of I are able to observe the signal, while the others ignore its ex_istence. For simplicity, we normalize the total number of landowners to 1, and we assume that a fraction β of the entire group observes the signal, while the remaining 1-β does not. The signal is essentially the perceived effect of some unspecified policy. In particular, this construction implicitly assumes that forest owners and managers regard any type of policy as affecting demand for wood and prices, and henceforth their expected values. For concreteness, here we will consider a policy viewed as beneficial that could possibly increase demand and prices, that is, s>0.

σ_s² is a measure of the precision of the signal, since higher σ_s² induces also higher variability of the signal and, therefore, lower precision (we refer the reader to [7] for the comparative statics analysis on σ_s²). However, notice that σ_s² could also be interpreted as the (inverse) degree of confidence into the policy maker.

α[0,1] represents the degree to which the signal is specific to the entire time horizon. If α=1, the signal is also partially informative about the long-run shock ε_a, and, consequently, about p₂. On the contrary, if α=0, the signal exclusively brings information contingent to time 1, and it cannot be used to infer the timber price realization at time 2. In concrete, one can imagine that, when the signal is announced, each forest owner (in group I) evaluates its degree of specificity.

The informativeness of the signal with respect to the demand and the timber price, respectively is defined as usual as γ^D=cov(s, D₁)/var(s) and γ^p=cov(s, p₂)/var(s). Given our assumptions, s, p₂|s and D₁|s are also normally distributed. In particular, standard Bayesian updating leads to:

p₂|s∼N(p₁(1+m)+sγ^p , (1-αγ^p)σ_a²+σ₂²) (3)

D₁|s∼N(D+sγ^D , (1-(α / D)γ^D)D₂σ_a²+(1-γD)σ_D²) (4)

If not explicitly mentioned otherwise, in the following we will assume that α≠0. Obviously, we also assume Q-D-sγ^D>0.

Landowners’ heterogeneity, information and equilibrium pricing

At the beginning of period 1, all the forest owners are endowed with a forest stock Q, and growth of the forest is described by (1) above. Each landowner invests the revenues p₁x^j ₁ from timbers harvested at time 1, x^j 1, in a risk free bond with gross return 1+r. Hence, within each group, the max_imization problem consists in choosing optimal current timber supply x^j 1, in order to max_imize the utility from final wealth w^j.

Given harvesting levels x^j ₁, x^j ₂, final wealth at time 2 is:

w^j=p₂x^j₂+ p₁x^j₁(1+b)

where x^j₂ is given by (1).

Before the harvesting and investment decisions are taken, members of group I receive some news concerning the forest sector by means of a signal s=αε_a+ ε_D + ε_s. This information is then used within the group to update the priors on D₁ and p₂, and henceforth to choose optimal contingent harvesting x_i¹. More generally, both groups choose optimal harvesting at time 1, given the available information Ω^j. In particular Ω^j is represented by the signal for landowners belonging to group I while it is an empty set for the others, so that ΩI=s and ΩNI=∅. The max_imization problem becomes:

Maxx_j¹ E[p₂x^j ₂+ p₁x^j ₁(1+b) |Ω^j ] j=I,NI

under the constraint given by (1).

Since p₁ is taken as given and p₂|Ω^j is normally distributed, so is w|Ω^j. Further, the utility index is a standard constant risk aversion exponential utility, so that the expected utility of w^j given information Ω^j is a strictly increasing transformation of the kernel E[w^j|Ω^j]-0.5 rVar[w^j|Ω^j].

The first order conditions associated to the max_imization problem (6) yield:

x_i 1=Q-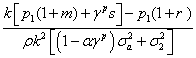(1)

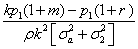xNI 1=Q- (2)

Clearly, an increase in the expected growth rate of timber prices m, or a reduction in the risk free rate b reduces the short-run timber supplies from both groups, x^I₁ and x^NI₁. Vice versa, an increase in the time 1 price p₁, or in the risk aversion coefficient r, or in the growth index k, increases both x^I₁ and x^NI₁, while an increase in the informativeness parameter α reduces x^I₁. The effect of an increase in risk (σ₂² and σ_a²) on the short-run supply of group NI is clear, leading to an increase in the time 1 supply x^NI₁. The effect on x^I₁ is generally the same; however, there exist combinations of parameters for which an increase in risk induces a reduction in x^I₁. Finally, when the signal is received, the informed group displays a lower supply at time 1 than the uninformed one, ceteris paribus.

The equilibrium price is computed by equalizing total timber supply at time 1, to the expected time 1 demand, given the available information, that is E[D₁| Ω j]. Specifically, assuming that the correct expected demand is indeed D+γDs, or, equivalently that the signal is not biased on purpose, the expected time 1 equilibrium price p* 1 solves the equation βx_i 1+(1-β)xNI 1=D+γDs, that is:

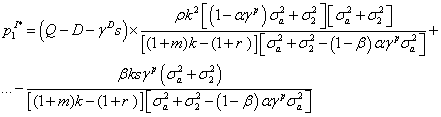(3)

Notice that, if the entire population was made by I forest owners, time 1 expected demand would still be E[D₁|s]= D+γDs., while it would be D if only the NI group was present. In these two particular cases, the expected equilibrium prices for the groups would be p^I*₁ and byp^NI*₁ respectively:

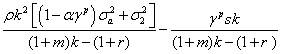(4)

p^NI*₁=(Q-D)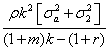 (5)

p^NI*₁ is also the equilibrium price that would realize if no signal was sent, in particular notice that p^I*₁NI*₁.

Neither the price p^I*₁ norp^NI*₁ realizes at the equilibrium, since the overall population of forest owners is in fact made up by the two groups.

In particular, p^I*₁*₁NI*₁, so that the heterogeneity of landowners’ population implies that the I (NI) group is asked to satisfy less than the entire demand, but at a higher (lower) price than p^I*₁ (p^NI*₁). An increase in β, that is, in the proportion of informed landowners reduces the equilibrium price as expected, in the extreme case of β=1, p^I*₁= p^*₁. This finding has concrete implications since it directly implies that increased information penetration reduces the (equilibrium) price for timber (Figure 1).

Figure 1: Expected value asymmetries: a harvesting behavior mode./p>

Expected value asymmetries: a harvesting behavior model

In this Section, we present a prototype tool based on the framework introduced above for general harvesting behavior forecasting and policy simulation. Our model, Expected Value Asymmetries, or shortly EVA, expands the framework analyzed above by considering five possible categories of forest owners, differing in terms of risk aversion and patience as regards postponing harvesting revenues, as detailed below. With the exclusive purpose of facilitating the analysis, the results presented here are based on the assumption that the initial growing stocks and growth rate are identical among the five categories. In what follows we will first detail the way we have expanded the framework introduced in the previous Sections, also providing a characterization of the five categories, and then present some result obtained from the analysis conducted in EVA.

As already mentioned, forest owners differ in their purposes, degree of information, and risk attitudes concerning their forests. To reflect this heterogeneity, we have assigned to each category of forest owners two coefficients: risk aversion, r, and degree of patience with respect to postponing harvesting income, q. In particular, we assign weights, 1-q and q, to monetary wealth from timber sale at time 1 and time 2, respectively, and we modify (5) assuming that individuals want to max_imize the utility of final weighted wealth w_q^j=(q)p₂x^j ₂+ +(1-q) p₁x^j₁(1+r), 0≤q≤1.

The use of the pair (1-q,q) allow us to express a degree of patience with respect to monetary outcomes realized in the future (as opposed to present ones), in particular, if q=0, the landowner only values monetary outcomes realized from current timber sale, while the opposite is true if q=1. When q=0.5 instead, monetary outcomes from current and future timber sale are equally valued. A higher degree of patience (0.5≤q<1) signalizes that the forest owner assigns the forest additional value beside the one provided by timber sales, and therefore is keen on carrying a larger forest stock to the future, even if this might not be optimal from a pure monetary perspective. This might be the case for example if the forest is part of an inheritance to be left to the children, or if has high ecological value, or if it provides non-monetary amenity services.

In creating forest owner typologies, we draw on earlier studies creating and analyzing private forest owner typologies [4-8]. We build in particular on Ingemarson et al. [7] in considering the following five categories of forest owners: Urban Dweller (UD), Economic Man, Elderly Couple, Green Values, and Multi-objective. In choosing the number and characteristics of forest owner categories, particular attention was made so as to allow sufficient variation as well as a continuum as regards objectives, and associated risk aversion and patience with respect to monetary outcomes. Here follows a brief description of the types:

I. Urban Dweller, being detached from his/her forest holding, has no clear objective with respect to his/her forest holding, and is not interested in, or receptive to, information/policies regarding forests. In light of the theoretical framework presented above, he/she belongs to the NI group. Since in essence the forest is not valued, risk aversion (r^UD) is low, for the same reason, the forest is left un-harvested in the first period, so that the patience coefficient q^UD is set to 1.

II. Economic Man has as overriding objective the max_imization of the monetary value of the forest, no matter if it comes from present or future timber sale, equivalently, the patience coefficient q^EM is at intermediate level. Risk aversion (r^EM) is also at intermediate level, and he/she is informed about possible policies affecting the timber market.

III. Elderly Couple’s main purpose is to leave the holding in as favorable (economic) condition for their children as possible. Consequently, the value of wealth from current timber sale is low (equivalently, patience (q^EC) is high) and risk aversion (r^EC) concerning future timber market conditions is high. For the same reasons, the Elderly Couple also tries to collect information on policies affecting the timber market.

IV. Green Values’ main objective is promoting non-timber values, e.g., biodiversity and r^ECreation. The value of monetary wealth from current timber sale, and consequently the opposite of patience (1-q^GV), is relatively small, since postponing final felling sustains nontimber values for a longer period. Risk aversion (r^GV) is fairly low. Information concerning timber markets is ignored, so that Green Value belongs to the NI group.

V. Multi-objective values both monetary and amenity (non-timber) benefits of forest holdings. Risk aversion (r^MO) is at intermediate/high levels and, due to amenity valuation, patience q^MO with respect to future timber sales is fairly high. Information about the future evolution of timber markets is collected and valued.

Next, we rank the five categories according to risk aversion (r) and the degree of patience with respect the future (q). From the lowest to the highest risk aversion (r) we have: Urban Dweller, Green Values, Economic Man, Multi-objective, and Elderly Couple (r^UDGVEMMOEC). Similarly, from the highest coefficient q to the lowest: Urban Dweller, Elderly Couple, Multi-objective, Green Values, and Economic Man (q^UD>qE >q^MO>q^GV >q^EM).

Since all groups max_imize the utility form economic wealth only, we assume that the risk aversion coefficient (r) ranges over 2 and 4, as typ_ically assumed in standard economic theory [22]. Therefore we assume: (Table 1).

Table 1: Preferences parameters per category: rUD, rGV rEM, rMO, rEC risk aversion coefficients for Urban Dweller (UD), Green Values (GV), Economic Man (EM), Multi-objective (MO) and Elderly Couple (EC); qUD, qGV qEM, qMO, qEC patience coefficients for Urban Dweller (UD), Green Values (GV), Economic Man (EM), Multi-objective (MO) and Elderly Couple (EC).

Next, we derive for each group the first order condition corresponding to the max_imization problem (6), wherein (5) has been replaced by the expression for final weighted wealth (wq j). We then solve for the equilibrium (i.e. for the optimal short run timber supply of each group and the equilibrium price) by setting to zero the system formed by the five first order conditions derived before and the market clearing condition that equalizes total period 1 supply to the expected demand.

It should be noted that the ranking and the numerical assignment to the various parameters are informed estimates only, based on a number of studies of forest owner attitudes [4-8]. For example, the high degree of the patience of the Elderly Couple is derived from Ingemarson et al. [7], where the category, or objectives cluster, ‘‘traditionalists’’, which insp_ired our Elderly Couple, is the one that to the largest extent expects children or other relatives to take over the forest estate. Accordingly, we assume that Elderly Couple, wishing to hand over a well-stocked forest holding, are less concerned with wealth from current timber sales.

In addition, a number of simplifications are implicitly assumed, such as inelastic demand and the absence of any budget or consumption requirements for the forest owners. However, as already pointed out, our purpose is not to launch a fully operative tool for policy-analysis, but rather to demonstrate some lines along which our theoretical framework could be elaborated for more applied research. In addition, there ex_ist studies providing an emp_irical basis for the quantification of some of the parameters, e.g., the distribution of growing stock on different owner categories (see, e.g., Favada et al. [9]).

In this section we present some of the research questions that could be addressed by the module EVA. We start by considering questions related to how forest owner heterogeneity affects the state of the forest resources and the timber market, and then we reassess the situation, considering also the effects of policy (unspecified, but with market implications).

Forest owner heterogeneity and forest development

Let us assume that the growing stock at time 1 is equally partitioned among the five categories, so that 20% of the growing stock (the one owned by Urban Dweller) is unmanaged, in the sense that no harvesting activities take place. Further, we assume that 20% of the entire growing stock is interesting from a biodiversity perspective (BIO in Figure 2), and it is entirely owned by a single category, while the remaining 60% is mainly valuable for timber (WOOD in Figure 2). We are interested in analyzing the composition of the growing stock at time 2, depending on whether the BIO area is owned by Multi-objective or Economic Man.

Figure 2: Initial growing stock composition.

The answer is provided in Figure 3a and 3b below: clearly, the unmanaged proportion (31.43%) is the same as this area is owned by the Urban Dweller in both examples, while if the BIO proportion is owned by Multi-objective, it will also represent a higher percentage of the total growing stock at time 2. Indeed, the higher degree of riskaversion of the Multi-objective with respect to the Economic Man would on one side induce a higher short-run harvest level; however, for this particular parameters’ assignment, this effect is more than compensated by the opposite one generated by the higher degree of patience of Multi-objective, which instead reduces short-time harvesting in favor of a higher growing stock available at time 2.

Figure 3: Time 2 growing stock composition (a) BIO area owned by Economic Man, (b) BIO area owned by Multi-Objective.

Though the quantitative findings strictly depend on the chosen values of the parameters, the results derived through the EVA model are interesting per se, in a qualitative sense. Indeed, in essence, the model simply computes the equilibrium, allowing for forest owner heterogeneity. The graphs above show that, independently from the numerical specifications adopted, such heterogeneity makes the distribution of forest land on owner types non-trivial. Hence, given that private forest owners are a heterogeneous group; our results highlight the necessity to consider forest ownership when producing policy analysis and forest resource outlooks.

Forest owner heterogeneity and the timber market

Next we compare how timber market characteristics (namely timber equilibrium price and market shares in the sense of shares of total timber supply) are affected by the heterogeneity in forest ownership. Specifically, we consider two alternative partitions of the forest growing stock: one that assigns 20% of the growing stock to Elderly Couple, 30% to Economic Man, and the remaining 50% equally between Multi-Objectives and Green Value, and one that assigns 30% of the growing stock to Elderly Couple, 20% to Economic Man, and the remaining 50% equally between Multi-Objectives and Green Value.

The equilibrium price that realizes in the second case is some 9% lower than the one realized under the first partition. This results from the intrinsic value of wood being lower for the Elderly couple, whose degree of patience with respect to the future is higher. Figure 4a and 4b below compare the market shares under the two possible partitions.

Figure 4: Market shares, (a) When the largest percentage (30%) of the growing stock is owned by Economic Man, (b) When the largest percentage (30%) of the growing stock is owned by Elderly Couple.

Forest owner’s heterogeneity and policy

When policy is considered, the EVA model accounts for the fact that different categories might have different degrees of confidence in the policy maker (1/σ_s² in the theoretical framework). Specifically, we rank those groups that are informed about forest policy according to their degree of confidence as follows (from the lowest to the highest): Elderly Couple, Multi-objective and Economic Man (as already mentioned, Green Values are assumed to be not receptacle for information that concerns timber market developments). In particular, σ²_EM=0.02, σ2MO=0.04, and σ²_EC=0.06.

Going back to the first example discussed in this Section, we assume that the BIO percentage is indeed owned by Economic Man, and that the policy maker would like to reduce the proportion of unmanaged stock and increase the one of BIO at time 2. The EVA model could then, e.g., be used for reassessing the composition of the growing stock, should the policy maker act in order to inform and train the Urban Dweller so that he/she will also eventually decide to harvest at time 1. Henceforth, the Urban Dweller is induced to assign value to his monetary wealth from harvesting at time 1, according to the patience coefficient q^UD=0.48, and his degree of confidence into the policy maker is pretty high with respect to the other categories, so that σ²_UD=0.03. The result of such a simulation is shown in Figure 5 below: the growing stock at time 2 is reduced by 8.55%, however such a reduction is mainly due to the decrease of unmanaged stock (-58.28%) since both the BIO and the WOOD proportions increase (by 79.5% and 20.4%, respectively).

Figure 5: Time 2 Growing stock composition after policy.

Next, we move to the third example considered above, and we analyze the effects on timber markets of two alternative policies: (a) one aimed at maintaining the actual market conditions and (b) one aimed at increasing the short-run supply of wood. The first policy consistently modifies the market shares (Figure 6a below), leaving the total supply unaffected, while the equilibrium price drops by some 14 percent. The second policy generates an additional minimal adjustment of the market shares (Figure 6b below) and a further reduction (3.8%) of the equilibrium price, while the short-run supply increases by 4.3% (and consequently the growing stock in the second period reduces 3.8%). Notice that this result might appear counterintuitive, however the contradiction is only illusory since the policy maker essentially acts as risk-reducer from a forest owner perspective.

Figure 6: Market shares, (a) After policy to keep total supply constant (30% of growing stock owned by Elderly Couple), (b) After policy aimed at increasing short-run timber supply (30% of growing stock owned by Elderly Couple).

In particular, the arrival of information (independently from its content) reduces the perceived variance as it appears in formula (3) and (4), and the results of our simulation also confirm this finding. Indeed, the introduction of the policy aimed at maintaining the actual market conditions reduces the first period’s individual supplies of all three informed groups (meaning of each landowner representing one of the three groups), as it appears in Figure 7, since the perceived variance of the second period’s price is reduced. Indeed, the absolute percentage variation in the short run supply is higher the higher is the coefficient of risk aversion (-13.1% for the Elderly Couple, -6.7% for Multi-Objective and -1.5% for the Economic Man). Next, when the second policy is put in place, the content of the information becomes relevant, and the informed landowners raise both the expected value of the demand and the one of the future price (for given equilibrium price).

Figure 7: An area matrix state transition model.

Hence the overall result is a priori ambiguous, since one should sum the effect of the reduced variance (i.e., reduction of short-run supply) to the one of increased expected value, which in itself is uncertain since the increase in the expected demand (future price) increases (decreases) the short-run supply. In our simulation these contrasting forces are represented by a period one supply which is lower than the one without but higher than the one under the first policy considered. Again, the simulation results, in quantitative terms, depend on the chosen parameter values. Nevertheless, in a qualitative sense, they demonstrate the necessity to take into account the heterogeneity of forest owners when issuing policy initiatives.

In this section it is outlined how EVA can integrate forest owner heterogeneity in an augmented DSS, linking a forest sector model with a forest resource assessment model.

EVA as part of a decision support system

The EVA model can work as an intermediary between a forest resource assessment model, (FRAM), such as, e.g., the European Forestry Dynamics Model (see https://gna.org/projects/efdm/) or EFISCEN [10], and an economic model for the forest sector (EMFS), such as, e.g., EFI-GTM [11]. In particular, EVA can complete the loop between the two models, using as inputs the max_imum harvestable level from the FRAM and the demand for wood primary products from the EMFS, and returning as output the amount effectively harvested by different forest-owner categories, to be ingested in the FRAM.

To explain the linkages between FRAM and EMFS more concretely, let us consider a FRAM belonging to the class of areamatrix state transition models as first developed in Sallnäs [23], such as the aforementioned European Forestry Dynamics Model or EFISCEN, meaning that a separate area matrix is assigned to each forest type according to region, owner type, species, site class (Figure 7). The FRAM derives the total max_imum harvestable level—given legal constraints, biodiversity considerations, etc.—ingested by the EMFS as upper bound to the supply of primary products (Figure 8).

Figure 8: EVA as part of a DSS.

Simultaneously, this information is also sent, at cell-level, to EVA along with information regarding forest growth rate and owner type, also at cell-level. EMFS derives the forest sector equilibrium and sends the demand for primary products to EVA. Given this information, for each cell EVA computes the amount to be harvested in order to maximize the utility from wealth of the respective forest owner under the resource constraint provided by FRAM and the requirement that the entire demand derived in FRAM has to be satisfied. EVA’s results are then fed back into FRAM completing the loop from EMFS to FRAM (Figure 8).

As knowledge concerning the distribution of forest land on different categories of forest owners is generally quite scant, ‘expert judgment’ is needed to allocate the forest resource on different owner types. Further, as already noted, the numerical assignment to the various parameters in EVA are to be regarded as informed estimates only. This lack of information makes frameworks as the one outlined above most suited for policy scenario analysis, since scenario analysis is better equipped to deal with indeterminacies caused by ignorance than, e.g., extrapolating methods [24,25].

Effective forest policy instruments require policy makers able to foresee what the harvesting reaction of private forest owners will be. This in turns depends on private forest owners’ specific attitudes and objectives. However, private forest owners do not constitute a homogenous group, as already noted in several studies. Ex_isting DSS do not account for forest owner heterogeneity, nor do they explicitly model the reaction of forest owners to market and/or policy signals

The current study seeks to address these shortcomings by (i) explicitly considering different types of forest owners, and by (ii) focusing on the role of information as a policy tool. A theoretical model of timber supply that studies how information releases affect harvesting behavior when forest owners differ in the awareness or receptiveness to this information is developed. Under these conditions, an asymmetry arises, which affects equilibrium pricing and, consequently, also harvesting decisions.

The theoretical model put forward permits information releases to influence forest owners’ expectations of timber demand and equilibrium pricing. Consequently, informed landowners display a lower short-run timber supply than uninformed ones, whereas increased information penetration lowers timber price. Thus, the framework has concrete policy implications, as it demonstrates how information can be used as a tool for influencing timber markets.

This theoretical framework is then expanded, allowing for a higher degree of heterogeneity in terms of forest owners’ preferences: we assume five forest owner types, differing as to (i) the responsiveness to market related information, (ii) risk aversion, and (iii) patience as regards postponing harvesting revenues. This harvesting behavior model, EVA, can, as a form of ‘artificial laboratory’, be used for policy analysis. Further, by working as an intermediary, EVA could provide feedback from an economic forest sector model to a forest resource assessment model, while at the same time ensuring that forest owner specific harvesting behavior is integrated in a DSS.

Simulation results derived through EVA indicate that the model is well adapted for modelling how forest owner heterogeneity and policy in the form of information release interact to affect the inter-temporal state of forest resources as well as the timber market. The numerical assignments to the various parameters of the EVA model are informed estimates only, derived from studies creating forest owner typologies. Further, in the simulation the distribution of forest land on the different categories is completely arbitrary.

Hence, though there are some studies providing emp_irical support for the quantification of some of the parameters, more emp_irically based knowledge, with a greater geographical coverage - concerning risk preferences, receptiveness to market-related information, and the distribution of forest land on different types of forest-owners - would enhance simulation models like EVA and contribute to the implementation of effective policy instruments. Imperfect information makes EVA and modelling frameworks as the one outlined above mostly suited for policy scenario analysis, since scenario analysis is better equipped to deal with indeterminacies caused by ignorance than, e.g., extrapolating methods [24,25]. This, however, is a caveat valid for most, if not all, modelling activities

List of Symbols

• U: utility function;

• r: risk-aversion coefficient

• w^j: wealth at time 2 for an individual belonging to group j

• I: index identifying the group of informed landowners

• NI: index identifying the group of uninformed landowners

• x^j_i: quantity harvested at time i by a generic landowner belonging to group j

• x^j₁: quantity harvested at time 1 by a generic landowner belonging to group j

• x^j₂: quantity harvested at time 2 by a generic landowner belonging to group j

• x^NI₁: quantity harvested at time 1 by a generic landowner belonging to group NI

• x^I₁: quantity harvested at time 1 by a generic landowner belonging to group I

• k: forest growth rate

• Q: initial forest endowment

• D₁: time 1 demand for wood

• D₂: time 2 demand for wood

• p_i: price at which wood harvested at time i is sold on the wood market

• p₁: price at which wood harvested at time 1 is sold on the wood market

p₂: price at which wood harvested at time 2 is sold on the wood market

• b: risk-free rate

• ε_a: long-run economic shock

• ε_D: time 1-contingent shock

• ε₂: time 2-contingent shock

• σ_a²: variance of the long-run economic shock ε_a

• σ_D²: variance of time 1-contingent shock ε_D

• σ₂²: variance of time 2-contingent shock ε₂

• m: price variation coefficient

• s: signal

• ε_s : noise of the signal

• σ_s²: variance of the noise ε_s

• β: fraction of the owners’ population that observes the signal

• α: degree to which the signal is specific to the entire time horizon

• γ^p: informativeness of the signal with respect to the timber price

• γ^D: informativeness of the signal with respect to the timber demand

• Ω^j: time 1 available information a generic landowner belonging to group j

• p^I*₁: expected equilibrium price at time 1 for a landowner belonging to group I

• p^NI*₁: expected equilibrium price at time 1 for a landowner belonging to group NI

• p^*₁: expected market time 1-equilibrium price

• q: degree of patience with respect to postponing harvesting income

• w_q^j: weighted wealth at time 2 for a landowner belonging to group j with patience coefficient q

• r^UD: risk-aversion coefficient for the “Urban Dweller” category

• r^GV: risk-aversion coefficient for the “Green Value” category

• r^EM: risk-aversion coefficient for the “Economic Man” category

• r^MO: risk-aversion coefficient for the “Multi Objective” category

• r^EC: risk-aversion coefficient for the “Elderly Couple” category

• q^UD: patience coefficient for the “Urban Dweller” category

• q^GV: patience coefficient for the “Green Value” category

• q^EM: patience coefficient for the “Economic Man” category

• q^MO: patience coefficient for the “Multi Objective” category

• q^EC: patience coefficient for the “Elderly Couple” category

• σ²_UD: inverse of the degree of confidence in the policy maker patience coefficient for the “Urban Dweller” category

• σ²_EM: inverse of the degree of confidence in the policy maker patience coefficient for the “Economic Man” category

• σ²_MO: inverse of the degree of confidence in the policy maker patience coefficient for the “Multi Objective” category

σ²_EC: inverse of the degree of confidence in the policy maker patience coefficient for the “Elderly Couple” category

The authors declare no conflict of interest. The op_inions expressed herein are those of the authors and do not necessarily reflect the views of the European Commission.