International Journal of Advancements in Technology
Open Access

Information Theory and its Role in Data Processing and Communication

Fan Kai^{* *}Correspondence: Fan Kai, Department of Computer Science, Aalborg University, Fredrik Bajers Vej, Denmark, Email:

Author info »

Description

Information theory is a mathematical framework for quantifying information and understanding how it can be stored, communicated and processed. Developed in the mid-20^th century by Claude Shannon, information theory has become an essential component in various fields, including telecommunications, data compression, cryptography and Machine Learning (ML).

Key concepts in information theory

Entropy: One of the central concepts of information theory is entropy, which measures the amount of uncertainty or randomness in a set of data. Shannon defined entropy as the average amount of information produced by a stochastic source of data. Mathematically, it is expressed as-

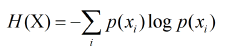
where H(X) is the entropy of the random variable X, and p(x_i) is the probability of occurrence of the possible outcomes x_i. Higher entropy indicates greater uncertainty, while lower entropy suggests more predictability in the data.

Redundancy: In the context of information theory, redundancy refers to the repetition of information within a dataset. While redundancy can be useful for error detection and correction, it can also lead to inefficient data storage and transmission. Information theory helps identify and minimize redundancy, allowing for more efficient encoding and transmission of data.

Channel capacity: Channel capacity is a measure of the maximum rate at which information can be transmitted over a communication channel without error. Shannon's channel capacity theorem states that there is a limit to how much information can be sent through a channel, depending on its bandwidth and noise level. The capacity C of a channel is given by-

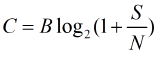
Source coding and data compression: Source coding involves encoding data to reduce its size without losing information. Techniques such as huffman coding and Lempel-Ziv-Welch (LZW) compression depend on principles of information theory to compress data efficiently. By minimizing redundancy and using variable-length codes, these techniques enable more efficient storage and transmission of information.

Error detection and correction: Information theory also plays a major role in error detection and correction. Communication channels can introduce noise, leading to errors in data transmission. Techniques such as hamming codes use principles of information theory to detect and correct errors, ensuring communication.

Applications of information theory

Information theory has far-reaching applications across various domains:

Telecommunications: The principles of information theory are fundamental in designing and optimizing telecommunications systems. Engineers use concepts like channel capacity to develop efficient encoding methods, ensuring high data transmission rates and minimizing errors.

Data compression: Information theory explains the algorithms used for data compression in various formats, such as images, videos and text files. By removing redundancy, these algorithms enable more efficient storage and faster transmission of data.

Cryptography: Information theory contributes to the field of cryptography by providing insights into secure communication. Concepts such as entropy help in understanding the strength of cryptographic keys and the unpredictability of generated keys, making systems more secure against attacks.

ML and Artificial Intelligence (AI): In the area of ML, information theory is applied to feature selection, model evaluation and loss functions. Techniques such as mutual information quantify the relationship between variables, helping to improve model accuracy and performance.

Biological Systems: Information theory has been used to analyze biological systems, particularly in understanding genetic information and biological communication processes. Researchers apply these concepts to study how information is encoded and transmitted in DNA and neural networks.

Conclusion

Information theory is an important discipline that has shaped our understanding of data communication and processing. From its foundational concepts like entropy and channel capacity to its wide-ranging applications in telecommunications, data compression, cryptography and ML, the impact of information theory is explainable. As technology continues to advance, the principles of information theory will remain central to addressing the challenges and opportunities that arise in an increasingly data-driven world. The exploration of new boundaries in this field, including quantum information theory, will further enhance our ability to manage and utilize information effectively.