Journal of Physical Chemistry & Biophysics
Open Access

Is PNP Theory Valid for a Black Hole Solution in Modified Gravity?

Surajit Das¹ and Surajit Mandal^{2* *}Correspondence: Surajit Mandal, Department of Physics, Jadavpur University, Kolkata, West Bengal, India, Email:

Author info »

Introduction

As is well-known, a Pseudo-Newtonian Potential (PNP) is a mathematical construction used in theoretical astrophysics to approximate the effects of general relativity in the motion of a massive particle near a black hole. In other words, most of the theoretical analysis of general theory of relativity in astronomy are studied by a Newtonian or pseudo-Newtonian method. It is called “Pseudo-Newtonian” because it has a form similar to the gravitational potential in Newtonian mechanics but it include additional terms that account for the curvature of space-time in general relativity. PNP’s are commonly used in studying the accretion of matter onto black holes and the dynamics of relativistic systems. To avoid the complication of full general relativistic equations, it is easier to use non-relativistic treatment but with the domination of corresponding (pseudo) potential which can simulate some relativistic effects consequent to the geometry of space-time. Using this potential one can obtain the approximate solutions of the hydrodynamical equations. Ghosh et al. [1], introduced such a Pseudo-Newtonian potential for a rotating Kerr black hole which is useful enough to reproduce the scenario of the classical mechanics [2-4]. PNP can replicate all the properties of an accretion disk near a black hole [4-7]. Chakraborty et al. [8], a few years back, introduced a general formalism of the trajectory of test particles around a general spherically symmetric non-rotating black hole, and as an example they considered non-rotating charged Reissner-Nordstrom black hole. It is worth mentioning that the general formulation of the trajectory is not only limited to standard general relativity but this formulation can also be extendable and applicable for any black hole solution in modified gravity theory. They did not extend the analysis considering the modified theories of gravity. This extended study was carried out by Mandal [9], considering a static black hole in f (R) gravity. It is interesting to generalize the results to other gravity models like Einstein-Gauss-Bonnet gravity and Lee-Wick gravity. Here in the present study, in order to generalize the previous result [9], we have extended this analysis considering other modified gravity and as an example we have considered a static and spherically symmetric 4D AdS Schwarzschild Yang- Mills Black Hole in Einstein-Gauss-Bonnet gravity.

In theoretical physics, theory of General Relativity (henceforth GR) by Einstein is one of the most successful theories. Despite its prominent achievements, there are still some unsolved challenging problems in the universe such as the cosmological constant problem, the hierarchy problem and the late time accelerated expansion of the Universe. This gleams that GR is not the ultimate theory and require further generalization. Addition of the higher curvature terms in the standard Einstein-Hilbert action is one of the possible generalization. Lovelock gravities can provided the higher curvature corrections of natural candidates and are the unique theories that execute generally covariant field equations [10]. Gauss-Bonnet gravity, also familiar as Einstein- Gauss-Bonnet (henceforth EGB), is the normal extension of the standard Einstein-Hilbert action to comprise higher curvature Lovelock terms. In string theory, a Gauss-Bonnet term arrives naturally in the low energy effective action [11]. Recently, Glavan and Lin formulated the EGB gravity in four dimensions as of higher dimensional field equation by rescaling the Gauss-Bonnet coupling constant α by α/D-4 [12]. Examples of some other higher order gravity theory are scalar-tensor theories [13-18], Brane world cosmology [19-21] and regular black holes [22-24]. Moreover, the charged AdS solution of EGB theory [25] for a complete study on 4D GB gravity [26]. Some of the other static and spherically symmetric black hole solutions and their phase transition, thermodynamics in 4D or higher dimensions EGB [27-33].

The consistent theory of 4D EGB gravity was studied in the studies of Aoki et al. [34,35]. Singh et al. [36], have studied on 4D AdS Einstein-Gauss-Bonnet black hole with Yang-Mills field and its thermodynamics. AdS charged black holes in Einstein-Yang-Mills gravity’s rainbow: Thermal stability and P-V criticality was studied by Hendi et al. [37]. Naeimipour et al. [38], studied on Yang-Mills black holes in Quasitopological gravity. Rotating Einstein-Yang- Mills black holes and black hole solution of Einstein-Born-Infeld- Yang-Mills theory can be found in the studies of Kleihaus et al. [39], and Meng et al. [40]. P-V criticality of a specific black hole in f (R) gravity coupled with Yang-Mills field was studied by Ovgun [41], and Aounallah et al. [42], have studied five-dimensional Yang-Mills black holes in massive gravity’s rainbow.

Methodolgy

Space-time structure of 4D AdS Schwarzschild Yang-Mills black hole for EGB gravity

In this section, we introduce the metric tensor of a static spherically symmetric black hole of the EGB gravity with the Yang-Mills field. The original theory of EGB gravity by Glavin and Lin [12], has been shown to not be self-consistent. The issue was resolved by Fernandes et.al. [43], and by Hennigar et.al. [44]. The D-dimensional EGB gravity in the presence of the Yang-Mills field is given by the following action,

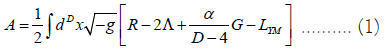
Where α is the Gauss-Bonnet coupling coefficient α ≥ 0; G is the Lagrangian density for EGB gravity (called Gauss-Bonnet invariant), given by,

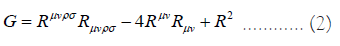
and Yang-Mills Lagrangian,

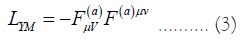
Which is given in terms of the Faraday–Maxwell tensor or electromagnetic field tensor F_μν described by 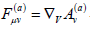with ∇_V representing the covariant derivative, and A(a) μ , the electromagnetic gauge field.

The equation of motion for the metric tensor 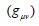and the electromagnetic potential 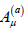are given by respectively,

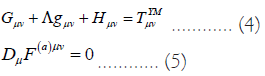
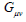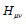Where and , are the Einstein tensor and the Lanczos tensor with the following expressions:

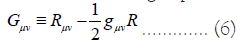
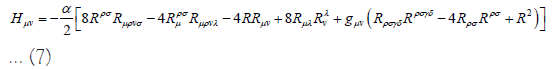
With R, 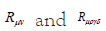represents the D=d+1 dimensional Ricci scalar, Ricci tensor and Riemann tensor respectively. On the other hand, the energy-momentum tensor due to the effect of Yang-Mills field is given by,

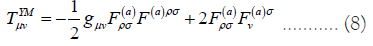
Now in order to get static spherically symmetric black hole solution for the EGB gravity with Yang-Mills field, we write the line element as,

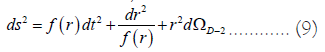
Where dΩ_D-2 denotes the metric of a (D-2)-dimensional sphere. The two branch solutions of metric potential for D → 4 has the following form [36]:

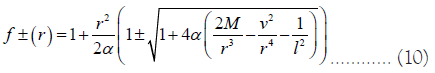
Where naturally adopted Λ in terms of scale length l as, 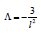for AdS solution. Since +ve signature of equation 10 is completely unphysical as it converted to Reissner-Nordstrom black hole having negative mass and imaginary charge. Hence we bound ourselves to the -ve branch of solution of equation 10, because the -ve signature reduces to the Schwarzschild solution for α → 0, ν → 0 and l → ∞. Also, from the above solution, in the limit of ν → 0 and l → ∞ we can be recovered the solution by Glavan and Lin [12]. Finally in α → 0, the metric function for AdS Schwarzschild Yang-Mills black hole becomes

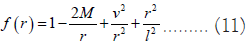
Here, M is an integration constant related to the black hole mass and ν is called Yang- Mills charge. However this solution reduces to the Schwarzschild black hole solution for ν=0 and l → ∞.

Here, we should note that the Yang-Mills case considered here corroborates with the case of an electrically charged black hole [45,46], because both yield the same metric function equation 10. However, AdS Schwarzschild Yang-Mills black hole corroborates with the Reissner-Nordstrom-AdS black hole [46]. Therefore, our study will be equally valid for Reissner-Nordstrom-AdS black hole case also.

Results and Discussion

Horizons of spacetime for 4D AdS Schwarzschild Yang- Mills black hole

The horizon of the AdS Schwarzschild Yang-Mills black hole equation 11 is given by setting f (r)=0. Now, we can plot the graph to estimate the horizons as shown in Figure 1. Figure 1 depicts the profile of metric function f (r) with radial coordinate r for five different values of Yang-Mills charge ν, when scale length is l=2 (left) and l=4 (right). It is evident from the figure that the radius of the outer horizon increases when the Yang-Mills charge ν decreases. In particular, all the plots are scaled with ν taking values of order 1. By doing elementary analysis of the zeros of f (r), Figure 1 shows that it has no zeros for ν>ν_c, one double zero if ν=ν_c and two simple zeros for ν<νc. It is evident, from the figure that the two horizons coincide at the critical radius,

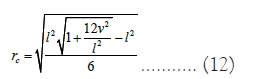
Figure 1: The behavior of f (r) versus r by changing ν for a fixed l=2, 1(a), In 1(b) the behavior of f (r) versus r by changing ν for a fixed l=4 is shown, taking M=1.

It is also evident that rc depends upon the parameters ν and l.

Relativistic theory: Energy and angular momentum

The basic relativistic theory of energy, angular momentum, and effective potential for a general static non-rotating black hole can be found in Refs [8,9]. Now, the energy and relativistic conserved angular momentum for circular orbits are respectively

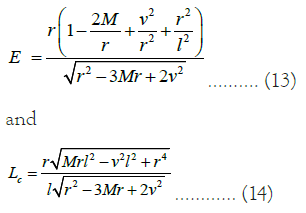
It is notified that both E_c and L_c depend on various parameters like Yang-Mills charge ν, scale length l, radial coordinate r and mass M of the AdS Schwarzschild Yang-Mills black hole. Figure 2a depicts the variation of relativistic angular momentum L_c with respect to changing r and ν, for a fixed l and Figure 2b depicts, the variation of relativistic angular momentum L_c with respect to changing r and l for a fixed ν. However, in Figure 3a, the variation of energy Ec with respect to changing r and ν for a fixed l and in Figure 3b, the variation of energy Ec with respect to changing r and l for a fixed ν are depicted.

Figure 2: (a) is the variation of relativistic angular momentum L_c with respect to changing r and ν for a fixed l=1, In (b) it is shown, the variation of relativistic angular momentum L_c with respect to changing r and l for a fixed ν=0.75, here, M=1.

Figure 3: In (a) the variation of energy Ec with respect to changing r and ν for a fixed l=1 is shown, In (b) the variation of energy Ec with respect to changing r and l for a fixed ν=0.75, taking M=1.

Now, relativistic specific angular momentum 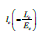can be calculated as

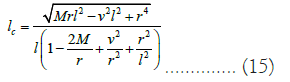
Effective potential Veff can be estimated as

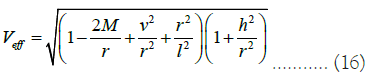
The nature of V_eff versus r by varying h, ν for fixed l is plotted in Figure 4. In both plots, V_eff increases for increasing ν.

Figure 4: In (a) and (b) the behavior of Veff with r by varying h, ν for constant l=1 is shown, M=1.

Pseudo-newtonian theory: Potential, energy and angular momentum

The basic PNP theory for a general static non-rotating and spherically symmetric black hole was studied in Refs [8,9]. The PNP and effective potentials, respectively, are,

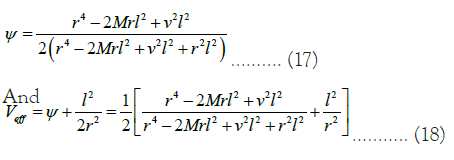
It can be easily observed by analyzing the boundary behavior of PNP ψ that when we approach spatial infinity,

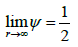
This is presented in Figures 5 and 6.

Figure 5: In (a) is the variation of PNP ψ with respect to changing r and ν for a fixed l=1, In (b) the variation of PNP ψ with respect to changing r and l for a fixed ν=0.75 is plotted, here, M=1.

Figure 6: In (a) the variation of PNP ψ with respect to r for changing ν for a fixed l=1 is shown, In (b) the variation of PNP ψ with respect to r for changing l for a fixed ν=0.75 is shown, taking M=1.

In Figure 5a, we plot PNP ψ for variation of both r and ν with l=1. In Figure 5b, the variation of PNP ψ for varying both r and l with ν=0.75 is plotted. Moreover, in Figure 6, we present the behavior of PNP with r for different values of ν (left figure) and l (right figure). Figure 6a shows that for lower values of r, PNP ψ will be increased when Yang-Mills charge ν will take larger values. On the other hand, from Figure 6b, it is clear that for lower r PNP ψ will be decreases for increasing values of scale length l. Both plots of Figures 5 and 6 also reveal that in the limit r → ∞, ψ clearly approaches to 1/2.

We obtain pseudo-Newtonian angular momentum as following:

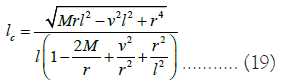
Figure 7a shows the variation of L_c for the variation of both r and ν with fixed l and Figure 7b shows the variation of L_c for the variation of both r and l with fixed ν.

Figure 7: (a) Plot of L_c with respect to r and ν for fixed l=1, In (b) plot of L_c with respect to r and l for fixed ν=0.75, taking M=1.

Now a comparative plot of L_c (from equation 14) and L_c (from equation 18) has been presented in Figures 8-11 for different values of ν and l. In Figures 8 and 9, ν and l are taken very small (up to the order of unity). On the other hand Figure 10 is for higher l, lower ν (top panel) and lower l, higher ν (bottom panel) while Figure 11 is for both higher l and higher ν. The solid curve (red) is for Pseudo-Newtonian angular momentum L_c and the dashed curve (blue) is for General Relativistic angular momentum L_c. From Figures 8 and 9, it is visible that for lower values of r, both the curves become asymptotical to L_c, L_c axis and for higher values of r the L_c curve is increasing whereas L_c curve become asymptotical to the radial coordinate axis. So it can be easily understood that L_c and L_c curve takes the same form for the lower values of r, however, both curve no longer matches for higher values of r. Interestingly Figure 10 (top panel) shows that for higher scale length l, both curves take the same form for all values of r whereas the bottom panel depicts that both curves have different behavior i.e., L_c curve is an increasing function of r while L_c curve is asymptotic to r-axis. Both of the curves of Figure 11, for higher l and higher ν, also take the same form [47-50].

Figure 8: (a), (b) and (c) are the variation of L_c and L_c with respect to r for changing l=3, 5, 10 but fixed ν=0.75 while (d), (e) and (f) is the plot of the variation of L_c and L_c with respect to r for changing l=3, 5, 10 but fixed ν=0.85, here, M=1.

Figure 9: (a), (b) and (c) are the variation of L_c and L_c with respect to r for changing ν=0.65, 0.75, 0.85, but fixed l=20, In (d), (e) and (f), the variation of L_c and L_c with respect to r for changing ν=0.65, 0.75, 0.85 but fixed l=15 is shown, here, M=1.

Figure 10: (a), (b) and (c), the variation of L_c and L_c with respect to r for changing ν=0.65, 0.75, 0.85 but fixed l=600 (high), (d), (e) and (f), the variation of L_c and L_c with respect to r for changing l=1, 5, 8 but fixed ν=80 (high), here, M=1.

Figure 11: The variation of L_c and L_c with r for changing ν=80, l=600 (a); ν=100, l=700 (b) and ν=120, l=800 (c) along with M=1.

It is worth mentioning that, PNP theory for 4D AdS Schwarzschild Yang-Mills black hole can reproduce the scenario of GR theory when both the scale length parameter l and Yang-Mills charge ν are taken low (valid for low ranges of r, but for higher ranges of r it does not reproduce the result any more) and also can simulate the GR theory when both of these parameters are taken high (for all values of r). However, for higher l and lower ν, we get the case of a Schwarzschild black hole. Finally, all results are verified for 4D AdS Schwarzschild Yang-Mills black hole solution in EGB gravity. The above result generalizes that the above analysis is not only restricted to Einstein’s gravity but it can also be extendable to black hole solution in any modified gravity theory [51-54].

Moreover, the expression for ec is given by [8,9],

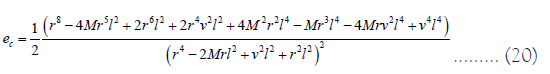
The positive roots of the following equation give marginally stable circular orbits:

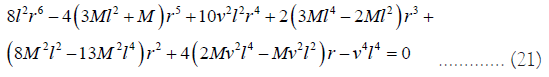
Finally, to get stable circular orbit we have the following condition:

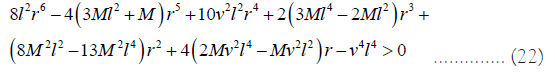
This analysis can also be applicable and extendable for any black hole in higher dimensions. For example, the metric for a N-dimensional black hole can be written as,

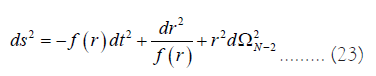
Where 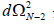represents the metric on unit (N-2) sphere, given by,

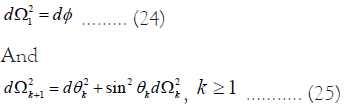
In this analysis, the motion of a test particle (massive or photon) should be restricted to the equatorial plane (θk=π/2, k ≥ 1), because of the fact that we have considered only spherical symmetry of the space-time. Therefore, in future work, an extension of the above approach for non-spherical system (especially axisymmetric) would be interesting.

Conclusion

In this paper, we outline space-time structure in EGB gravity and to get a deeper insight about the horizon, we plot lapse function with respect to the radial coordinate r. Using GR treatment, we calculate energy and angular momentum. Here we noticed that the energy and angular momentum depend on various parameters like scale length, Yang-Mills charge and mass of the black hole. To check the dependency of energy and angular momentum on these parameters we make a graphical analysis. Moreover, we determined the effective potential and graphical analysis shows that effective potential increases when Yang-Mills charge increases.

Within the context of PN theory, we determined PNP, angular momentum, and energy. Here it is also notified that PNP, energy, and angular momentum also depend on various parameters like scale length, Yang-Mills charge, and mass of the black hole. In this framework, we also made a graphical analysis of the energy and angular momentum. The graph of PNP for different values of ν and l shows that for lower values of r, PNP will be increased when Yang-Mills charge will take larger values and PNP will decrease for increasing values of scale length. Interestingly, in the limit r → ∞, PNP clearly approaches to 1. More importantly, we have presented a comparative plot of relativistic angular momentum L_c and PN angular momentum L_c for different values of scale length and Yang-Mills charge. The graph for lower values of Yang-Mills charge and scale length demonstrated that in both, the GR treatment and PN treatment, the angular momentum curve takes the same form only for lower ranges of r while both curves no longer match for higher ranges of r. These plots justify the PNP theory for 4D Schwarzschild Yang-Mills black hole for some lower values of r. The graph for both higher l and higher ν can justify the PNP theory for 4D Schwarzschild Yang-Mills black hole for the entire ranges of r. While the graph for higher values of scale length parameter and lower values of Yang-Mills charge demonstrated that both angular momentum curves take the same form for all ranges of r. These plots justify the PNP theory for Schwarzschild black hole.

We also noticed that a marginally stable circular orbit depends on the parameters like scale length, Yang-Mills charge, and mass of the black hole. It is important to note that, the general formulation of the general gravity theory was used very well to a black hole solution in EGB gravity. Our result generalizes that this analysis is not only restricted to Einstein’s gravity but it can also be extendable and applicable to black hole solution in any modified theories of gravity.

Acknowledgements

The author is thankful to S. Upadhyay for various suggestions which developed the presentation of the paper.

Conflicts of Interest

The authors declare no conflicts of interest. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. Ghosh S, Mukhopadhyay B. Generalized pseudo-newtonian potential for studying accretion disk dynamics in off-equatorial planes around rotating black holes: Description of a vector potential. Astrophys J. 2007;667(1):367.

   [Crossref] [Google Scholar]

2. Einstein A. Relativity: The special and general theory. Methuen and Co. Ltd. 1920.
3. Einstein A. The meaning of relativity. Am J Phys. 1950;1935:1. [Crossref]

   [Google Scholar] [PubMed]

4. Einstein A. Cosmological considerations on the general theory of relativity. Proceedings of the Royal Prussian Academy of Sciences. 1917:142-152.

   [Google Scholar]

5. Sarkar SS, Biswas R. Pseudo newtonian potential for a rotating kerr black hole embedded in quintessence. Eur Phys J C. 2019;79:1-24.

   [Crossref] [Google Scholar]

6. Ivanov RI, Prodanov EM. Pseudo-newtonian potential for charged particle in kerr–newman geometry. Phys Lett B. 2005;611(1-2):34-38.

   [Crossref] [Google Scholar]

7. Mukhopadhyay B. Description of pseudo-newtonian potential for the relativistic accretion disks around Kerr black holes. Astrophys J. 2002;581(1):427.

   [Crossref] [Google Scholar]

8. Chakraborty S, Chakraborty S. Trajectory around a spherically symmetric non-rotating black hole. Can J Phys. 2011;89(6):689-695.

   [Crossref] [Google Scholar]

9. Mandal S. Trajectory of massive particles around a static black hole in f (R) gravity. Europhys Lett. 2022;140(6):69001.

   [Crossref] [Google Scholar]

10. Lovelock D. The Einstein tensor and its generalizations. J Math Phys. 1971;12(3):498-501.

    [Crossref] [Google Scholar]

11. Zwiebach B. Curvature squared terms and string theories. Phys Lett B. 1985;156(5-6):315-317.

    [Crossref] [Google Scholar]

12. Glavan D, Lin C. Einstein-Gauss-Bonnet gravity in four-dimensional spacetime. Phys Rev Lett. 2020;124(8):081301.

    [Crossref] [Google Scholar]

13. Barrabes C, Bressange GF. Singular hypersurfaces in scalar-tensor theories of gravity. Class Quant Grav. 1997;14(3):805.

    [Crossref] [Google Scholar]

14. Capozziello S, Troisi A. Parametrized post-Newtonian limit of fourth order gravity inspired by scalar-tensor gravity. Phys Rev D. 2005;72(4):044022.

    [Crossref] [Google Scholar]

15. Moffat JW. Scalar–tensor–vector gravity theory. J Cosmol Astropart Phys. 2006;2006(3):004.

    [Crossref] [Google Scholar]

16. Sotiriou TP. f (R) gravity and scalar–tensor theory. Class Quant Grav. 2006;23(17):5117.

    [Crossref] [Google Scholar]

17. Faraoni V. de Sitter space and the equivalence between f (R) and scalar-tensor gravity. Phys Rev D. 2007;75(6):067302.

    [Crossref] [Google Scholar]

18. Cai RG, Myung YS. Black holes in the Brans-Dicke-Maxwell theory. Phys Rev D. 1997;56(6):3466.

    [Crossref] [Google Scholar]

19. Cline JM, Firouzjahi H. Brane-world cosmology of modulus stabilization with a bulk scalar field. Phys Rev D. 2001;64(2):023505.

    [Crossref] [Google Scholar]

20. Nihei T, Okada N, Seto O. Neutralino dark matter in brane world cosmology. Phys Rev D. 2005;71(6):063535.

    [Crossref] [Google Scholar]

21. Demetrian M. False vacuum decay in a brane world cosmological model. Gen Rel Grav. 2006;38:953-962.

    [Crossref] [Google Scholar]

22. Tangphati T, Pradhan A, Banerjee A, Panotopoulos G. Anisotropic stars in 4D Einstein–Gauss–Bonnet gravity. Phys Dark Universe. 2021;33:100877.

    [Crossref] [Google Scholar]

23. Tangphati T, Pradhan A, Errehymy A, Banerjee A. Anisotropic quark stars in Einstein-Gauss-Bonnet theory. Phys Lett B. 2021;819:136423.

    [Crossref] [Google Scholar]

24. Pretel JM, Banerjee A, Pradhan A. Electrically charged quark stars in 4 D Einstein–Gauss–Bonnet gravity. Eur Phys J C. 2022;82(2):180.

    [Crossref] [Google Scholar]

25. Fernandes PG. Charged black holes in AdS spaces in 4D Einstein Gauss-Bonnet gravity. Phys Lett B. 2020;805:135468.

    [Crossref] [Google Scholar]

26. Fernandes PG, Carrilho P, Clifton T, Mulryne DJ. The 4D Einstein–Gauss–Bonnet theory of gravity: A review. Class Quant Grav. 2022;39(6):063001.

    [Crossref] [Google Scholar]

27. Hegde K, Kumara AN, Rizwan CL, Ali MS. Thermodynamics, phase transition and Joule Thomson expansion of novel 4-D Gauss Bonnet AdS black hole. arXiv preprint. 2020.

    [Crossref] [Google Scholar]

28. Singh DV, Ghosh SG, Maharaj SD. Clouds of strings in 4D Einstein–Gauss–Bonnet black holes. Phys Dark Universe. 2020;30:100730.

    [Crossref] [Google Scholar]

29. Panah BE, Jafarzade K, Hendi S. Charged 4D Einstein-Gauss-Bonnet-AdS black holes: Shadow, energy emission, deflection angle and heat engine. Nucl Phys B. 2020;961:115269.

    [Crossref] [Google Scholar]

30. Godani N, Singh DV, Samanta GC. Stability of thin-shell wormhole in 4D Einstein–Gauss–Bonnet gravity. Phys Dark Universe. 2022;35:100952.

    [Crossref] [Google Scholar]

31. Singh DV, Siwach S. Thermodynamics and Pv criticality of Bardeen-AdS black hole in 4D Einstein-Gauss-Bonnet gravity. Phys Lett B. 2020;808:135658.

    [Crossref] [Google Scholar]

32. Wang YY, Su BY, Li N. Hawking–page phase transitions in four-dimensional Einstein–Gauss–Bonnet gravity. Phys Dark Universe. 2021;31:100769.

    [Crossref] [Google Scholar]

33. Wei SW, Liu YX. Extended thermodynamics and microstructures of four-dimensional charged Gauss-Bonnet black hole in AdS space. Phys Rev D. 2020;101(10):104018.

    [Crossref] [Google Scholar]

34. Aoki K, Gorji MA, Mukohyama S. Cosmology and gravitational waves in consistent D→ 4 Einstein-Gauss-Bonnet gravity. J Cosmol Astropart Phys. 2020;2020(09):014.

    [Crossref] [Google Scholar]

35. Aoki K, Gorji MA, Mukohyama S. A consistent theory of D→ 4 Einstein-Gauss-Bonnet gravity. Phys Lett B. 2020;810:135843.

    [Crossref] [Google Scholar]

36. Singh DV, Singh BK, Upadhyay S. 4D AdS Einstein–Gauss–Bonnet black hole with Yang–Mills field and its thermodynamics. Ann Phys. 2021;434:168642.

    [Crossref] [Google Scholar]

37. Hendi SH, Momennia M. AdS charged black holes in Einstein–Yang–Mills gravity's rainbow: Thermal stability and P−V criticality. Phys Lett B. 2018;777:222-234.

    [Crossref] [Google Scholar]

38. Naeimipour F, Mirza B, Masoumi Jahromi F. Yang–Mills black holes in quasitopological gravity. Eur Phys J C. 2021;81(5):455.

    [Crossref] [Google Scholar]

39. Kleihaus B, Kunz J, Navarro-Lérida F. Rotating Einstein-Yang-Mills black holes. Phys Rev D. 2002;66(10):104001.

    [Crossref] [Google Scholar]

40. Meng K, Yang DB, Hu ZN. Black hole solution of Einstein-Born-Infeld-Yang-Mills theory. Adv High Energy Phys. 2017;2017.

    [Crossref] [Google Scholar]

41. Övgün A. P-V Criticality of a specific black hole in f (R) gravity coupled with Yang-Mills field. Adv High Energy Phys. 2018;2018.

    [Crossref] [Google Scholar]

42. Aounallah H, Pourhassan B, Hendi SH, Faizal M. Five-dimensional Yang–Mills black holes in massive gravity’s rainbow. Eur Phys J C. 2022;82(4):351.

    [Crossref] [Google Scholar]

43. Fernandes PG, Carrilho P, Clifton T, Mulryne DJ. Derivation of regularized field equations for the Einstein-Gauss-Bonnet theory in four dimensions. Phys Rev D. 2020;102(2):024025.

    [Crossref] [Google Scholar]

44. Hennigar RA, Kubizňák D, Mann RB, Pollack C. On taking the D→ 4 limit of Gauss-Bonnet gravity: theory and solutions. J High Energy Phys. 2020;2020(7):1-18.

    [Crossref] [Google Scholar]

45. Saffari R, Rahvar S. f (R) gravity: From the pioneer anomaly to cosmic acceleration. Phys Rev D. 2008;77(10):104028.

    [Crossref] [Google Scholar]

46. Soroushfar S, Saffari R, Kunz J, Lämmerzahl C. Analytical solutions of the geodesic equation in the spacetime of a black hole in f (R) gravity. Phys Rev D. 2015;92(4):044010.

    [Crossref] [Google Scholar]

47. Stuchlík Z, Hledík S. Some properties of the Schwarzschild–de Sitter and Schwarzschild–anti-de Sitter spacetimes. Phys Rev D. 1999;60(4):044006.

    [Crossref] [Google Scholar]

48. Stuchlík Z. The motion of test particles in black-hole backgrounds with non-zero cosmological constant. Astronomical Institutes of Czechoslovakia, Bulletin. 1983;34(3):129-149.

    [Google Scholar]

49. Roupas Z. The gravothermal instability at all scales: From turnaround radius to supernovae. Universe. 2019;5(1):12.

    [Crossref] [Google Scholar]

50. Arraut I. The astrophysical scales set by the cosmological constant, black-hole thermodynamics and non-linear massive gravity. Universe. 2017;3(2):45.

    [Crossref] [Google Scholar]

51. Bhattacharya S, Dialektopoulos KF, Romano AE, Skordis C, Tomaras TN. The maximum sizes of large scale structures in alternative theories of gravity. J Cosmol Astropart Phys. 2017;2017(07):018.

    [Crossref] [Google Scholar]

52. Faraoni V. Turnaround radius in modified gravity. Phys Dark Universe. 2016;11:11-15.

    [Crossref] [Google Scholar]

53. Stuchlík Z, Hledik S, Novotný J. General relativistic polytropes with a repulsive cosmological constant. Phys Rev D. 2016;94(10):103513.

    [Crossref] [Google Scholar]

54. Stuchlík Z, Schee J. Influence of the cosmological constant on the motion of Magellanic clouds in the gravitational field of milky way. J Cosmol Astropart Phys. 2011;2011(09):018.

    [Crossref] [Google Scholar]