Journal of Chromatography & Separation Techniques
Open Access
ISSN: 2157-7064
ISSN: 2157-7064
Research Article - (2013) Volume 4, Issue 5
Carbon prepared from waste plants for the treatment of dyeing industry effluents has high significance in environmental sustainability and economic viability. Methylene Blue (MB) in aqueous solutions was subjected to color removal by the adsorption technique onto activated sunflowers seeds shell carbon (SSSC) as agricultural material. Results obtained indicate that the removal efficiency of Methylene Blue varies from 92.7 to 95.6% by rising the temperature from 30 to 60°C at pH from 6 to 8. The results fit the BET model for adsorption of Methylene Blue on SSSC, verify the assumption that the adsorbate molecules could be adsorbed in more one layer thick and non homogenous on the surface of the adsorbent. A comparison of kinetic models (pseudo first-order, the pseudo secondorder, Elovich and intraparticle diffusion) at different conditions showed that the pseudo second-order kinetic model correlate the experimental data well. Van’t Hoff equation was used to evaluate the thermodynamic parameters (ΔH, ΔS, and ΔG), which indicate that adsorption processes for the present work are exothermic, and this is agreement with the stability of adsorption capacity with temperature, chemically in nature, and spontaneous.
Keywords: Adsorption; Isotherms; Kinetic models; Thermodynamics; Sunflowers seeds shell
A: Constant describing the energy of interaction between solute and adsorbent surface;
C: Initial concentration (mg/l);
Ce: Concentration equilibrium (mg/l);
Cs: Saturation concentration of solute (mg/l);
KF&n: Freundlich constants;
m: Weight of adsorbent (mg);
k1: Rate constant of pseudo first-order adsorption (l/min);
k2: Rate constant of pseudo second-order adsorption (g/mg. min);
KD: Distribution coefficient (cm3.g-1)
kid: Intraparticle diffusion rate constant (min-1);
KL: Constant related to the adsorption/desorption energy (l g-1);
qe: Adsorption capacity at equilibrium, (mg of dye/g adsorbate);
qmax: Maximum sorption (mg of dye/g adsorbate);
qt: Adsorption capacity at time t, (mg of dye/g adsorbate);
R: universal gas constant (j/mole. K);
R: Percent (MB) adsorbed;
t: Contact time (min);
V: Volume of the solution;
x: Amount of solute adsorbed (mg);
Xm: Amount of solute adsorbed in forming a complete mono layer (mg of dye/g adsorbate);
α: Initial adsorption rate (mg of dye/g adsorbate. min);
β: Desorption constant (g/mg) during any experiment;
The hulls, or shells, of Sunflower Seed are mostly composed of cellulose. They decompose slowly. They are sometimes burned as biomass fuel. Sunflower seeds are more commonly eaten as a healthy snack than as part of a meal. They can also be used as garnishes or ingredients in various recipes. The seeds may be sold as in-shell seeds or dehulled kernels [1].
Cationic dyes, such as Methylene Blue (MB), were used initially for dyeing of silk, leather, plastics, paper, and cotton mordant with tannin, as well as for the production of ink and copying paper in the office supplies industry [2]. In the textile sector, an estimated 10-20% of dyes (active substance) used is lost in residual liquors through the exhaustion and washing operations [3]. The releasing of dyes to the environment can cause acute and/or chronic effects on the exposed organisms, adsorb or reflect sunlight entering into water, and thus result in change of food chain [4].
Previous studies found that MB molecules existed as dimer or as aggregates at the surface, as well as a protonated form depending on the concentration and the surface properties [5]. Such extensive use of dyes and pigments often poses problems in the form of colored wastewater that require pre-treatment for color removal prior to disposal into receiving water bodies or publicly owned treatment works [6]. The main problem for dyestuff manufacturers and users is the removal or reducing the quantity of color in effluent and water sources [7].
At the present time there is no single process capable of adequate treatment [8]. Most of the existing processes include adsorption, usually with activated carbon (AC) [9]. The adsorption of the cationic dye, MB, has been used for a long time for the evaluation of the adsorption properties of AC, and in monitoring the production and quality of AC prepared from coal, in fluidized bed [10,11]. Adsorption from dilute aqueous solutions onto solid surfaces is a highly attractive separation technique for many applications, such as wastewater treatment, liquid mixture separation and purification, or polar organic solutes recovery from biotechnology processes [12,13]. In particular, adsorption provides a technique of great interest to remove dyes from municipal and industrial wastewater [14,15]. This can be achieved by using adsorbents with a high adsorptive capacity and selectivity [16].
The adsorption process can be either physical or chemical in nature, and frequently involves both. Physical adsorption involves the attraction by electrical charge differences between adsorbent and the adsorbate. Chemical adsorption is the product of a reaction between the adsorbent and the adsorbate [17]. In recent years, stringent government regulations have made it mandatory to stop such effluents, unless they are treated properly; hence, the removal of color from the effluent discharge has become environmentally important [18,19].
Preparation of (SSSC)
The dried Sunflowers Seeds shells ware soaked in a boiling solution of 10% H3PO4 for one hour and kept at room temperature for 24 h. Thereafter, the wood material was separated, air dried at room temperature and carbonized in muffle furnace at 400°C for 20 min. The carbon was ground to powder and activated in a muffle furnace at 800°C for a period of 10 min. Then the activated carbon was washed with plenty of distilled water to remove residual acid, and dried at 105°C. The washed carbon ware lightly ground in a mortar and sieved through 0.5 mm and 0.05 mm diameter by means of a test sieve shaker respectively.
Batch adsorption studies
Batch experiments with SSSC were conducted to investigate the parameters effects of initial adsorbate particle size and concentration, adsorption time, pH, temperature on MB adsorption. All reagents used were of analytical reagent (AR) grade (Sigma-Aldrich, Germany). MB samples were prepared by dissolving a known quantity of the dye in distilled water and used as a stock solution and diluted to the required initial concentration (range: 25 to 125 mg/l). 50 ml of MB solution of known concentration (co) was taken in a 100 ml conical flask with the required amount of adsorbent and was shaken for different time intervals in a shaker at different pH values and different temperatures. Then, the solution was filtered through a filter paper. UV-visible spectrophotometer (model PHTOMECH 301-D+) was employed to determine the remaining concentrations of MB in the filtrate at 670 nm.
Adsorption Isotherms Study
Equilibrium studies that give the capacity of the adsorbent and adsorbate are described by adsorption isotherms, which is usually the ratio between the quantity adsorbed and that remained in solution at equilibrium at fixed temperature. Freundlich, Langmuir and BET isotherms are the earliest and simplest known relationships describing the adsorption equation [20-28]. Adsorption isotherms have been classified into six characteristic types. Microporous adsorbents produce adsorption isotherms of Type 1 (which has a convex shape) and it is also associated with monomolecular layer adsorption. Types II and III depict adsorption for multi-molecular layer formation while Types IV and V describe the adsorption process of multi-molecular layer formation and condensation in pores. Type VI represents surface phase transition of a monomolecular layer on a homogeneous surface [29].
Langmuir isotherm
The Langmuir equation is used to estimate the maximum adsorption capacity corresponding to complete monolayer coverage on the adsorbent surface and is expressed by:
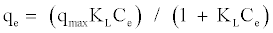 (1)
(1)
The linearise form of the above equation after rearrangement is given by:
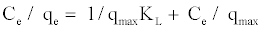 (2)
(2)
The experimental data is then fitted into the above equation for linearization by plotting Ce/qe against Ce.
Freundlich isotherm
The Freundlich model named after Freundlich (1926) [30] is an empirical equation used to estimate the adsorption intensity of the sorbent towards the adsorbate and is given by:
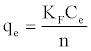 (3)
(3)
Also, the value of n indicates the affinity of the adsorbate towards the adsorbent. The above equation is conveniently used in linear form as:
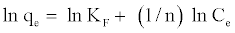 (4)
(4)
A plot of ln Ce against ln qe yielding a straight line indicates the conformation of the Freundlich adsorption isotherm. The constants 1/n and ln KF can be determined from the slope and intercept, respectively.
BET isotherm
The BET derived an adsorption isotherm based on the assumption that the adsorbate molecules could be adsorbed in more than one layer thick on the surface of the adsorbent [31]. Their equation, assumed that the energy of adsorption holds the first monolayer but that the condensation energy of the adsorbate is responsible for adsorption of successive layers. The equation, known as the BET equation, is commonly written as follow:
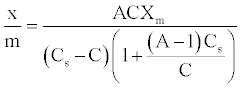 (5)
(5)
or
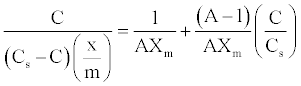 (6)
(6)
Thus, plotting [C/(Cs-C)]/(x/m) against C/Cs will give rise to straight lines with slope (A-1)/AXm and intercept 1/AXm for adsorption processes that conform BET equation [23].
The study of adsorption dynamics describes the solute uptake rate and evidently this rate controls the residence time of adsorbate uptake at the solid-solution interface. Kinetics of MB adsorption on the SSSC was analyzed using pseudofirst-order, pseudo second-order, Elovich and intraparticle diffusion kinetic models [32,33].
The pseudo first-order model
The pseudo first-order equation [34] is generally expressed as follows:
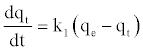 (7)
(7)
At t=0 to t=t and qt=0 to qt=qt, the integrated form of Equation (7) becomes:
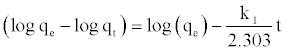 (8)
(8)
where k1 and qe can be determined from the slope and intercept of the plot.
The pseudo second-order model
The pseudo second-order kinetic rate equation is expressed as [35]:
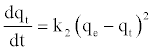 (9)
(9)
At t=0 to t=t and qt=0 to qt=qt, the integrated form of Equation (9) becomes:
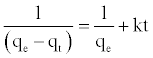 (10)
(10)
Equation (4) can be rearranged to obtain Equation (11), which has a linear form:
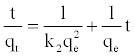 (11)
(11)
If the initial adsorption rate, h (mg/g. min) is:
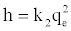 (12)
(12)
then Equations (11) and (12) become:
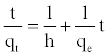 (13)
(13)
The plot of (t/qt) and t of Equation (11) should give a linear relationship from which qe and k2 can be determined from the slope and intercept of the plot, respectively.
The Elovich model
The Elovich model equation is generally expressed as:
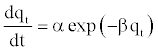 (14)
(14)
To simplify the Elovich equation, [36] assumed αβt >> t and by applying the boundary conditions t=0 to t=t and qt=0 to qt=qt, Equation (14) becomes:
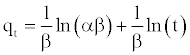 (15)
(15)
A plot of qt vs. ln(t) should yield a linear relationship with a slope of (1/β) and an intercept of (1/β) ln(αβ).
The intraparticle diffusion model
The intraparticle diffusion model is expressed as [37]
 (16)
(16)
A linearized form of the equation is obtained as:
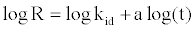 (17)
(17)
If MB adsorption fits the intraparticle model, a plot of log R vs. log t should yield a linear relationship with a slope of a and an intercept of log kid.
General information of SSSC
A Cross sections through and Scanning electron micrographs for activated sunflowers seeds shell carbon was shown in Figures 1 and 2 with magnification scale of 500.
Adsorption isotherms
The results of this study show that SSSC was effective, in adsorbing MB as its removal reached 95.6% at 60°C and dye initial concentration of 50 mg/l. Adsorption of MB was highly pH-dependent and the results showed that the optimum pH for the removal was found to be 6-8, at which MB exists mostly as the most easily adsorbed form aqueous solution increases as the initial MB concentration. Also increasing temperature, smaller adsorbate particle were found to increase the percentage removal of MB. The Experimental data were applied in the three isotherms (Figures 3-5), which results indicate that the adsorption of MB on SSSC fits the BET model with r2=0.978, verifying the assumption that the adsorbate molecules could be adsorbed in more than one layer thick on the surface of the adsorbent.
Adsorption dynamics
Effect of adsorbate concentrations: The removal of MB by adsorption on SSSC was found to increase with time and attained a maximum value at 150 min. On changing the initial concentration of MB solution from 25 to 125 mg/l, the amount adsorbed increased at 30°C, pH 7 and particle size of 0.05 mm. The experimental results correlate with the theoretically predicted curves. Results obtained show good compliance with the pseudo second-order kinetic model (Figure 6), with values of correlation coefficient, r2 ≅ 0.99.
Effect of adsorbent particle size: The batch adsorption experiments were carried out using adsorbent with different particle sizes, (blew 0.05 to over 0.5 mm) at pH 7, 30°C, and initial concentration of 25 mg/l. The removal of MB increased with the decrease in particle size. The data obtained separately for each of the kinetic models from the slopes of plots, show a good compliance with the pseudo second-order equation (Figure 7), with values of correlation coefficient, r2 ≅ 0.99.
Effect of temperature: Increasing the temperature is known to increase the rate of diffusion of the adsorbate molecules across the external boundary layer and in the internal pores of the adsorbent particle, owing to the decrease in the viscosity of the solution.
In addition, changing temperature will change the equilibrium capacity of the adsorbent for a particular adsorbate. The experimental data were obtained at pH 7, particle size blew 0.05 mm, and initial concentration of 25 mg/l. The increasing adsorption rate of MB on the surface of SSSC may be explained by considering more conversion of the dimer species to monomers. The data obtained for each of the kinetic models from the slopes of plots (Figure 8) show a good compliance with the pseudo second-order equation, with values of correlation coefficient, r2>0.99.
Effect of adsorbent dose: MB uptake was studied using different doses of SSSC by using 50 ml of solution at pH 7, 30°C, particle size blew 0.05 mm and initial concentration of 25 mg/l. The concentrations used were 0.5, 0.75, 1, 1.25 and 1.5 gm adsorbent/ liter adsorbate, keeping the batch experimental volume the same in all cases. The results indicated that the percent adsorption increased with the increase in SSSC dose. The curves (Figure 9), showed good compliance with pseudo secondorder model with values of correlation coefficient, r2 ≅ 0.99.
Effect of pH: The removal of MB was studied at different pHs in the range 3-11 by SSSC at initial MB concentration of 25 mg/l, and a temperature of 30°C, particle size blew 0.05 mm. The variation in adsorption capacity in this pH range is largely due to the influence of pH on the adsorption characteristics of the SSSC which indicates that the adsorption capacity of the adsorbent is clearly pH dependent. The optimum removal (95%) was observed in the pH range 6-8. Results also showed that the adsorption reaction can be approximated with the pseudo second-order kinetic model (Figure 10), with values of correlation coefficient, r2 ≅ 0.99. The rate constants and values of correlation coefficient represented in Table 1.
| Parameter | First order | Second order | Elovich model | Intraparticle diffusion | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | r2 | qe | K2 | r2 | b | α | r2 | kid | a | r2 | ||
| pH | 3 | -0.0112 | 0.954 | 32.68 | 0.0009 | 0.997 | 0.144 | 2.13 | 0.991 | 12.15 | 0.3373 | 0.992 |
| 6 | -0.0093 | 0.922 | 37.17 | 0.0010 | 0.992 | 0.1508 | 5.16 | 0.974 | 21.93 | 0.2519 | 0.988 | |
| 7 | -0.0119 | 0.961 | 41.49 | 0.0021 | 0.999 | 0.2031 | 90.01 | 0.947 | 46.94 | 0.1414 | 0.949 | |
| 8 | -0.0067 | 0.812 | 45.05 | 0.0003 | 0.975 | 0.0992 | 1.19 | 0.879 | 6.7 | 0.4727 | 0.951 | |
| 11 | -0.0073 | 0.722 | 57.47 | 0.0001 | 0.469 | 0.0954 | 0.64 | 0.78 | 1.94 | 0.6753 | 0.912 | |
| particlesize (mm) | 0.05 | -0.0119 | 0.962 | 41.49 | 0.0021 | 0.999 | 0.2031 | 90.01 | 0.947 | 46.94 | 0.1414 | 0.949 |
| 0.125 | -0.0062 | 0.941 | 34.48 | 0.0023 | 0.999 | 0.2575 | 95.08 | 0.967 | 39.73 | 0.1344 | 0.977 | |
| 0.16 | -0.0084 | 0.877 | 34.01 | 0.0015 | 0.991 | 0.2020 | 14.03 | 0.943 | 28.53 | 0.1882 | 0.962 | |
| 0.2 | -0.0092 | 0.896 | 32.68 | 0.001 | 0.985 | 0.1616 | 11.92 | 0.961 | 16.27 | 0.2802 | 0.983 | |
| 0.315 | -0.0118 | 0.977 | 37.31 | 0.0003 | 0.995 | 0.1123 | 0.89 | 0.996 | 3.65 | 0.5634 | 0.982 | |
| Adsorbent dose (mg/l) | 0.5 | -0.0115 | 0.936 | 59.52 | 0.0008 | 0.995 | 0.1061 | 16.68 | 0.976 | 22.58 | 0.2095 | 0.986 |
| 0.75 | -0.0111 | 0.926 | 42.37 | 0.0013 | 0.994 | 0.1650 | 20.12 | 0.943 | 22.45 | 0.2724 | 0.982 | |
| 1 | -0.0107 | 0.949 | 32.89 | 0.002 | 0.996 | 0.2304 | 28.55 | 0.955 | 32.29 | 0.1634 | 0.965 | |
| 1.25 | -0.0084 | 0.84 | 33.01 | 0.0014 | 0.986 | 0.2125 | 14.41 | 0.898 | 35.00 | 0.1842 | 0.923 | |
| 1.5 | -0.0119 | 0.962 | 27.70 | 0.0032 | 0.999 | 0.3047 | 60.01 | 0.947 | 46.94 | 0.1414 | 0.949 | |
| Conc.(mg/l) | 25 | -0.0138 | 0.989 | 51.81 | 0.0003 | 0.989 | 0.0784 | 1.37 | 0.906 | 31.00 | 0.1872 | 0.97 |
| 50 | -0.0186 | 0.926 | 34.84 | 0.0012 | 0.991 | 0.1676 | 6.38 | 0.930 | 23.67 | 0.2335 | 0.938 | |
| 75 | -0.0099 | 0.977 | 70.42 | 0.0002 | 0.974 | 0.0605 | 1.91 | 0.970 | 4.93 | 0.5011 | 0.983 | |
| 100 | -0.0114 | 0.953 | 71.94 | 0.0002 | 0.999 | 0.0587 | 1.80 | 0.998 | 3.88 | 0.5384 | 0.991 | |
| 125 | -0.0051 | 0.996 | 45.05 | 0.0003 | 0.987 | 0.095 | 1.355 | 0.983 | 2.89 | 0.4759 | 0.993 | |
| Temp.(°C) | 30 | -0.0084 | 0.941 | 42.02 | 0.0013 | 0.996 | 0.1615 | 17.44 | 0.980 | 35.343 | 0.1902 | 0.989 |
| 40 | -0.0095 | 0.951 | 42.37 | 0.0014 | 0.997 | 0.1669 | 23.51 | 0.986 | 38.09 | 0.1793 | 0.992 | |
| 50 | -0.0125 | 0.919 | 41.67 | 0.002 | 0.999 | 0.213 | 127.24 | 0.975 | 48.85 | 0.1336 | 0.977 | |
| 60 | -0.0124 | 0.907 | 41.84 | 0.0022 | 0.999 | 0.2145 | 141.32 | 0.953 | 49.63 | 0.1317 | 0.955 | |
Table 1: The adsorption kinetic model rate constants.
Thermodynamic parameters
Determination of ΔH°, ΔS° and ΔG°: The values of the thermodynamic parameters, enthalpy variation (ΔH) and entropy variation (ΔS), were calculated from the curve relating the distribution coefficient (KD) as a function of temperature (Figure 9) using the equation:
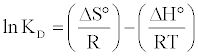 (18)
(18)
where KD is the distribution coefficient (cm3.g-1), defined as:
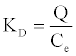 (19)
(19)
where Q is the amount adsorbed (mg adsorbate/g adsorbent) described by the equation:
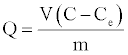 (20)
(20)
where C and Ce are the initial and equilibrium concentrations of the solute, respectively (mg.cm-3). The calculated data for KD and Q are shown in Table 2.
| Temperature (°C) | Q | KD |
|---|---|---|
| 30 | 38 | 12.67 |
| 40 | 38.5 | 15.4 |
| 50 | 39 | 19.5 |
| 60 | 39.4 | 21.89 |
Table 2: Q and KD parameters at different temperatures.
The free energy change (ΔG°) parameter was calculated using equation 21:
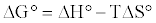 (21)
(21)
From Figure 11 the values of ΔH°, ΔS° were determined from the slopes and intercepts of the curves, respectively as well as the calculated values of ΔG° and are listed in Table 3. Investigation of the obtained values of the thermodynamic parameters shows that the adsorption process is exothermic. This is in accordance with increasing adsorption equilibrium with increasing temperature.
| ΔHkcal/mol | ΔS kcal/mol. K. | ΔG (kcal/mol) | |||
|---|---|---|---|---|---|
| 30°C | 40°C | 50°C | 60°C | ||
| -0.058 | 0.211 | -64.1 | -66.2 | -68.36 | -70.45 |
Table 3: Thermodynamic parameters at different temperatures.
Determination of mean free:
I. Energy (E)
The mean free energy of adsorption (E) is the free energy change when one mole of ions is transferred to the surface of the membrane from infinity in the solution and it is calculated from:
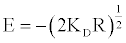 (22)
(22)
The mean free energies (E) were calculated and documented in Table 4.
| Temperature (°C) | KD | E, kj/mol |
|---|---|---|
| 30 | 12.67 | 7.08 |
| 40 | 15.4 | 7.81 |
| 50 | 19.5 | 8.88 |
| 60 | 21.89 | 9.31 |
Table 4: Free Energy (E) at different temperatures.
The magnitude of E is useful for estimating the type of sorption reaction, since E<8 kJ. mol-1, physical forces such as diffusion processes may affect the sorption mechanism [24]. So, the adsorption of dyes seems to be a complex phenomenon, where diffusion and chemical bonding occur at different temperature ranges, this may support that the monolayer capacity (qmax) increases with increasing temperature. But in our work the results indicate a rapprochement of the activation energy with 8 which indicate small influence of the adsorption with temperature increasing. Table 5 shows some of the adsorption capacities of low-cost adsorbents reported in the literature.
| Sorbent | qmax (mg g-1) |
|---|---|
| Degreased coffee bean | 55.3 |
| Treated sawdust | 65.8 |
| Arundo donax root carbon | 8.69 |
| Activated charcoal | 0.179 |
| Waste apricot | 116.27 |
| Activated carbons commercial grade | 8.27 |
| Laboratory grade activated carbons | 42.18 |
| Bentonite | 7.72 |
| Sugarcane dust | 4.88 |
| Hen feathers | 26.1 |
| Iron humate | 19.2 |
| Rubber wood sawdust | 36.45 |
| Cellulose | 2.422 |
| Neem leaf powder | 133.6 |
| Ricinus communis | 27.78 |
| Lemon peel | 51.73 |
| Caulerpa racemosa var. cylindracea | 26.57 |
| Rattan sawdust | 62.7 |
| Maize cob powder | 37.037 |
| Sea shell powder | 42.33 |
| Salix Leafs powder | 62.35 |
| activated sunflowers seeds shell carbon, (present work) | 39.4 |
Table 5: Comparison between adsorption capacity of low-cost adsorbents.
• Sunflowers Seeds shells Carbon (SSSC) could be used as an alternative low cost adsorbent of dyes from industrial wastewater discharged from dying units.
• The adsorption process fits the BET model, corroborating the assumption that the adsorbate molecules could be adsorbed in more than one layer thick on the surface of the adsorbent.
• The kinetics of MB adsorption on the SSSC was found to follow a pseudo second-order rate equation.
• The mean free energies (E) revealed that, adsorption of dyes on SSSC seems to be a complex phenomenon, where diffusion and chemical bonding occur at different temperature ranges.
• The values of thermodynamic parameters indicate that all adsorption processes are exothermic, and this is in agreement with the stability of adsorption capacity with temperature.
• Thermodynamic studies are performed and the values of the parameters suggest that the process of removal of MB by SSSC is a spontaneous one.