Journal of Chromatography & Separation Techniques
Open Access
ISSN: 2157-7064
ISSN: 2157-7064
Research Article - (2013) Volume 4, Issue 7
The removal of methylene Blue (MB) in aqueous solution by the adsorption technique onto date palm fibers (DPF) as agricultural waste material was studied. Results obtained indicate that the removal efficiency of Methylene Blue varies from 93.8 to 98.5% by rising the temperature from 30 to 60°C at pH from 6 to 8. The results fit the Langmuir model for adsorption of MB on DPF. A comparison of kinetic models (pseudo first-order and the pseudo second-order) at different conditions showed that the pseudo second-order kinetic model correlate the experimental data well. Van’t Hoff equation was used to evaluate the thermodynamic parameters (ΔH, ΔS, and ΔG), which indicate that adsorption process is endothermic in nature.
Keywords: Adsorption; Isotherms; Kinetic models; Thermodynamics; Date palm fibers
C0: Initial concentration (mg/l); Ce: Equilibrium concentration (mg/l); DPF: Date Palm Fibers; MB: Methelyne Blue; KF&n: Freundlich constants; M: Weight of adsorbent (mg); k1: Pseudo first-order adsorption rate constant (l/min); k2: Pseudo second-order adsorption rate constant (g/mg/min); KD: Distribution coefficient (cm3g-1); KL: Langmuir constants (L mg-1); Q: Adsorption capacity (mg of dye/g adsorbate); qe: Adsorption capacity at equilibrium, (mg of dye/g adsorbate); qmax: Maximum adsorption (mg of dye/g adsorbate); qt: Adsorption capacity at time t (mg of dye/g adsorbate); R: Gas constant (8.314 J/mol/K); RL: The essential features of the Langmuir isotherm; T: Temperature (K); t: Contact time (min); V: Volume of the solution; r2: Correlation coefficient
Dyes are widely used in many industries such as rubber, textile, plastic, paper etc. Among these various industries, Textile industries have shown a significant increase in the use of synthetic complex organic dyes as colouring materials [1]. The conventional treatment processes for colour removal typically include physical, chemical and biological schemes. However, these processes were very expensive and could not be effectively used to treat the wide range of dyes waste [2]. The adsorption process is one of the effective methods for separation and purification. The removal of coloured and colourless organic pollutants from industrial wastewater is considered as an important application of adsorption processes [3]. Activated carbon (powdered or granular) is the most widely used adsorbents because it has excellent adsorption efficiency of the organic compound. Nevertheless, commercially available activated carbon is very expensive [4].
In recent years, there is a growing interest in using low cost, ecofriendly materials and commercially available adsorbent materials for the adsorption of dyes such as orange peel, neem leaves and bananapeel [5], hardwood [6], wool fiber and cotton fiber [7], banana pith [8], tamarind fruit shell [9], rice husk [10], silk cotton hull, coconut tree sawdust [11], coir pith [12], neem (AzadirachtaIndica) husk [13] and peat [14]. The objective of this research was to investigate the removal of methylene blue (MB) from aqueous solutions by using date palm fibers (DPF). The equilibrium, kinetics and thermodynamics of the adsorption process were studied.
Preparation of the adsorbent
Date palm fibers (DPF) were collected from trunk of date palm tree. DPF wascut into small pieces, washed with distilled water to remove dirt and dried at 80°C to remove moisture content. After drying process, DPF were ground and sieved to different particle size using Vibratory Sieve Shaker (AS 200 Control, Retsch).
Dye solution preparation
Samples of Methylene Blue (MB) (Figure 1) were prepared by dissolving a known quantity in distilled water and used as a stocksolution (1000 mg L-1), and diluted to the required initial concentration (range: 50 to 150 mg L-1). All reagents used were of AR grade (Sigma-Aldrich, Germany). The remaining concentrations of MB in the centrifuged solution were determined using UV-visible spectrophotometer (model PHTOMECH301-D+) (Figure 1).
Batch adsorption studies
Batch experiments were carried out to investigate the parametric effects of adsorbent particle size, adsorbent dose, contact time, pH, temperature, and initial MB concentration for adsorption on DPF. 50 ml of a MB solution of known concentration (C0) wastaken in a 100 ml conical flask with a required amount of adsorbent and was shacked for different time in a thermostatic shaking water bath (SHZ- 82), at different pH and Temperature. The samples were withdrawn and centrifuged at 5000 rpm for 5 min and the supernatant solutions were analyzed. Experiments were carried out at initial pH value is 7.5 and was controlled by using either 0.1N NaOH or 0.1 N HCl.
The adsorption percent (%) was calculated according to the following equation:
Adsorption percent (%)=[(C0-Ce)/C0]×100 (1)
In addition, the adsorption capacity (q) is calculated according to the following equation:
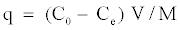 (2)
(2)
Where,
C0=initial concentration of solute (mg/L)
Ce=equilibrium concentration of solute (mg/L)
V=volume of solution (L)
M=mass of adsorbent (g)
Adsorption isotherms study
Equilibrium studies that give the capacity of the adsorbent are described by adsorption isotherms. Langmuir and Freundlich isotherms are the earliest and simplest known relationships describing the adsorption equation.
Langmuir isotherm: The Langmuir isotherm assumes that the sorption is monolayer and the strength of the intermolecular attractive forces is believed to fall off rapidly with distance [15].
Langmuir model is represented as:
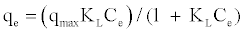 (3)
(3)
Where, qe is the amount of MB adsorbed per unit weight of adsorbent (mg g-1), Ce is the concentration of MB in solution at equilibrium (mg L-1), KL is the Langmuir constant and related to adsorption capacity and energy of adsorption (L mg-1) and qmax is attained concentrations corresponding to monolayer coverage.
Equation (3) can be described by the linearized form:
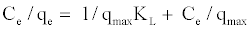 (4)
(4)
By plotting (Ce/qe) versus Ce, give a straight line of slope 1/qmax and intercept (1/qmaxKL). The essential features of the Langmuir isotherm can be expressed in terms of a dimensionless constant term (RL) [16].
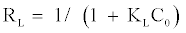 (5)
(5)
RL values within the range 0
Freundlich isotherm: The expression of the Freundlich model is [17]:
qe=KF Ce(1/n) (6)
KF[(mg/g)/(mg/l)] and 1/n is the Freundlich constant related to the adsorption capacity of DPF, and n is an empirical parameter refers to adsorption tendency.
Equation (6) can be linearized in logarithmic form (7):
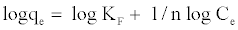 (7)
(7)
By plotting Logqe versus Log Ce, the constant KF and 1/n can be determined from the intercept and slope of the straight line, respectively.
Adsorption kinetics
Kinetics of MB adsorption on the DPF was analyzed using pseudo first-order and pseudo second-order models. The conformity between experimental data and the model predicted values was expressed by the correlation coefficients (r2, values close or equal to 1). A relatively high r2 value indicates that the model successfully describes the kinetics of (MB) adsorption [18,19].
Pseudo-first-order model: The pseudo first order kinetic model was given by equation:
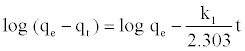 (8)
(8)
Where, qe and qt (mg/g) refer to the amount of dye adsorbed at equilibrium and at time t, respectively; k1 is the rate constant of pseudo first order (min-1). Values of k1 and qe were calculated from the slope and intercept values of the straight line of plotting log (qe-qt) versus t.
Pseudo-second-order model: The sorption data were also analyzed in terms of pseudo-second order model [19,20], given by the equation:
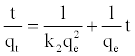 (9)
(9)
Where, k2 is the overall rate constant of the pseudo second order adsorption (g/mgmin-1). The plot of t/qt versus t should give a straight line and the pseudo second order rate constant k2 and equilibrium adsorption capacity qe were calculated from the values of intercept and slope, respectively.
Adsorbent characterizations
Raw DPF (Figure 2a), was studied using scanning electron microscopy (SEM), in the Figure 2b, this figure showed that the DPF has a rough, Wrinkly and porous surface with many yarns and cells, allowing for good adsorption between DPF and dye.
Equilibrium adsorption isotherm
The linearized form of Langmuir and Freundlich adsorption isotherms obtained at different temperature and pH are shown in Figures 3 and 4, respectively, whereas the adsorption constants evaluated from the isotherms with the correlation coefficients are given in Table 1. The Langmuir isotherm model appears to be the best fitting model for adsorption of MB on DPF because it gives the highest correlation coefficient value than Freundlich isotherm model.
| Variable | Langmuir isotherm model parameter | Friendlier isotherm model parameter | |||||||
|---|---|---|---|---|---|---|---|---|---|
| qmax | KL | RL | r2 | KF | n | r2 | |||
| Temperature | |||||||||
| 30°C | 3.83 | 9.01 | 0.0024 | 0.991 | 4.92 | 17.24 | 0.912 | ||
| 40°C | 4.26 | 7.04 | 0.0016 | 0.995 | 4.87 | 20.40 | 0.935 | ||
| 50°C | 4.74 | 6.01 | 0.0033 | 0.975 | 4.85 | 29.41 | 0.946 | ||
| 60°C | 5.02 | 5.53 | 0.0036 | 0.997 | 4.79 | 35.71 | 0.949 | ||
| pH | |||||||||
| 5 | 3.61 | 1.091 | 0.0179 | 0.986 | 5.86 | 5.81 | 0.93 | ||
| 6 | 3.89 | 5.025 | 0.0039 | 0.995 | 4.94 | 14.92 | 0.87 | ||
| 7.5 | 4.56 | 13.69 | 0.0014 | 0.999 | 4.98 | 7.93 | 0.68 | ||
| 8 | 4.51 | 17.01 | 0.0011 | 0.945 | 5.10 | 13.69 | 0.90 | ||
| 9 | 3.11 | 0.245 | 0.0751 | 0.966 | 5.49 | 6.66 | 0.91 | ||
| Adsorbent particle size (mm) | |||||||||
| 0.150 | 4.56 | 7.191 | 0.0166 | 0.988 | 4.88 | 7.85 | 0.90 | ||
| 0.355 | 3.79 | 9.225 | 0.0123 | 0.985 | 4.91 | 10.96 | 0.89 | ||
| 0.5 | 3.56 | 14.69 | 0.0030 | 0.999 | 4.99 | 12.93 | 0.75 | ||
| 2.0 | 2.51 | 19.41 | 0.0022 | 0.965 | 5.22 | 13.69 | 0.80 | ||
| Adsorbent dose (mg) | |||||||||
| 0.5 | 4.61 | 3.088 | 0.0109 | 0.976 | 5.75 | 8.83 | 0.89 | ||
| 1.0 | 3.39 | 6.045 | 0.0059 | 0.995 | 5.31 | 10.94 | 0.90 | ||
| 1.5 | 2.46 | 10.69 | 0.0034 | 0.998 | 4.98 | 11.95 | 0.88 | ||
| 2.0 | 1.9 | 14.01 | 0.0023 | 0.977 | 5.01 | 13.69 | 0.92 | ||
| Adsorbate concentration (mg/l) | |||||||||
| 50 | 3.85 | 6.650 | 0.0199 | 0.986 | 5.80 | 12.81 | 0.91 | ||
| 75 | 3.78 | 5.760 | 0.0133 | 0.993 | 4.98 | 14.95 | 0.90 | ||
| 100 | 4.11 | 10.65 | 0.0083 | 0.998 | 5.22 | 17.22 | 0.88 | ||
| 125 | 3.51 | 16.09 | 0.0045 | 0.985 | 5.10 | 20.69 | 0.85 | ||
| 150 | 3.03 | 21.24 | 0.0013 | 0.976 | 5.21 | 25.65 | 0.91 | ||
Table 1: Langmuir and Freundlich isotherm constants for adsorption of MB onto DPF.
Adsorption dynamics
Effect of adsorbate concentrations: The removal of MB by adsorption on DPF was found to increase with time and attained a maximum value at 40 min. On changing the initial concentration of MB solution from 50 to 150 mg/l, the amount adsorbed increased from 4.82 mg/g to 12.25 mg/g at 30°C, pH 7.5 and particle size >0.150 mm. From Table 2 and Figure 5, show good compliance with the pseudo second-order kinetic model with values of correlation coefficient, r2>0.980.
| Parameter | Pseudo first-order (Lagergren) | Pseudo second-order | |||||
|---|---|---|---|---|---|---|---|
| K1 | qe | r2 | K1 | qe | r2 | ||
| pH | 5 | 0.0667 | 3.475 | 0.933 | 0.0196 | 5.154 | 0.991 |
| (Condition: dye = 50mg L-1, >0.150, V = 50 mL, mass = 0.3 g, 3 h, 30°C) | 6 | 01036 | 2.218 | 0.953 | 0.0439 | 5.463 | 0.980 |
| 7.5 | 0.1266 | 3.033 | 0.914 | 0.0388 | 5.649 | 0.980 | |
| 9 | 0.1013 | 2.331 | 0.965 | 0.0251 | 5.813 | 0.968 | |
| 12 | 0.1102 | 4.572 | 0.966 | 0.0273 | 4.273 | 0.984 | |
| Adsorbent particle size (mm) | 0.150 | 0.1243 | 2.897 | 0.922 | 0.0396 | 4.950 | 0.981 |
| Condition: dye = 50 mg L-1, V = 50 mL, 60 min, pH= 4, mass= 0.3 g, 30°C) | 0.355 | 0.1013 | 1.166 | 0.907 | 0.0542 | 4.760 | 0.997 |
| 0.5 | 0.1804 | 1.142 | 0.912 | 0.0409 | 4.530 | 0.996 | |
| 2.0 | 0.2340 | 1.114 | 0.871 | 0.0132 | 3.980 | 0.982 | |
| Adsorbent dose (mg) | 0.5 | 0.1266 | 2.471 | 0.878 | 0.092 | 5.152 | 0.999 |
| Condition: dye = 50 mg L-1, V =50 mL , 60 min, pH= 4, >0.150, 30°C) | 1.0 | 0.1311 | 1.728 | 0.943 | 0.088 | 4.620 | 0.967 |
| 1.5 | 0.1773 | 1.520 | 0.832 | 0.085 | 4.532 | 0.986 | |
| 2.0 | 0.1427 | 1.365 | 0.921 | 0.072 | 4.321 | 0.985 | |
| Temperature (°C) | 30 | 0.1266 | 3.033 | 0.914 | 0.0426 | 4.932 | 0.996 |
| Condition: dye = 50 mg L-1, >0.150, V = 50 mL, 60 min, pH= 4, mass = 0.3 g) | 40 | 0.1450 | 3.120 | 0.908 | 0.1095 | 5.012 | 0.997 |
| 50 | 0.1105 | 2.233 | 0.937 | 0.130 | 5.132 | 0.999 | |
| 60 | 0.1128 | 3.190 | 0.942 | 0.135 | 5.189 | 0.998 | |
| Adsorbate concentration (mg/l) | 50 | 0.1410 | 7.128 | 0.831 | 0.0545 | 5.465 | 0.994 |
| Condition: pH= 4, V = 50 mL, mass = 0.3 g, >0.150, 60 min, 28°C) | 75 | 0.1335 | 7.231 | 0.900 | 0.0455 | 7.874 | 0.999 |
| 100 | 0.1232 | 7.580 | 0.851 | 0.0407 | 10.416 | 0.998 | |
| 125 | 0.0437 | 4.395 | 0.829 | 0.0107 | 12.790 | 0.989 | |
| 150 | 0.0391 | 4.295 | 0.769 | 0.0115 | 12.822 | 0.987 | |
Table 2: Kinetics data for adsorption of MB onto DPF.
Effect of adsorbent particle size: The batch adsorption experiments were carried out using PDF with different particle sizes, (>0.150, >0.355, >0.5, and >2.0 mm) at pH 7.5, 30°C, and initial concentration of 50 mg/l. The uptake of MB increased with the decrease in particle size. The relatively higher adsorption with smaller adsorbent particle may be attributed to the fact that smaller particles yield large surface areas [18]. The results obtained for each of the kinetic models from the slopes of the plots (Figure 6), show a better compliance with the pseudo second-order equation, the r2 values for the linear plots being >0.982 showed that kinetic data fitted the pseudo second-order adsorption kinetic equation (Table 2).
Effect of adsorbent dose: The removal of MB by adsorption on DPF was studied using different doses of DPF by using 50 ml of solution at pH 7.5, 30°C, particle size >0.150 mm and initial concentration of 50 mg/l. The adsorbent doses were 0.5, 1.0, 1.5, and 2.0 gm/50 ml of MB solution. The results indicated that the adsorption percent increased withincrease in DPF dose.
The results (Figure 7), showed good compliance with the pseudo second-order kinetic model with values of correlation coefficient, r2>0.985. The rate constants and values of correlation coefficient are represented in Table 2.
Effect of temperature: The temperature has two major effects on the adsorption process. Increasing the temperature is known to increase the rate of diffusion of the adsorbate molecules across the external boundary layer and in the internal pores of the adsorbent particle, owing to the decrease in the viscosity of the solution. In addition, changing temperature will change the equilibrium capacity of the adsorbent for a particular adsorbate [18].
The experimental data were obtained at pH 7.5, particle size >0.150 mm, and initial concentration of 50 mg/l. The results indicate that increasing the temperature of the solution caused an increase of the uptake of MB. Figure 8 show a better compliance with the pseudosecondorder equation, the r2 values for the linear plots being >0.996 showed that kinetic data fitted the pseudo second-order adsorption kinetic equation (Table 2).
Effect of pH: The uptake of MB at different pHs by DPF was at an initial MB concentration of 50 mg/l, a temperature of 30°C, and particle size >0.150 mm. The variation in adsorption capacity in this pH range is due to the influence of pH on the adsorption characteristics of the PDF which indicates that the adsorption capacity of the PDF is clearly pH dependent. The optimum pH was observed by 98% MB uptake at pH 6-8. Results also show a good compliance with the pseudo secondorder model (Figure 9). The rate constants and values of correlation coefficient are represented in Table 2, which indicated that the values of correlation coefficient were, r2>0.980.
Thermodynamic studies
Thermodynamic parameters, such as enthalpy variation (ΔH°), entropy variation (ΔS°) and change in Gibbs free energy (ΔG°), were calculated from the curve relating the distribution coefficient (KD) as a function of temperature (Figure 10), using the equations [18,20].
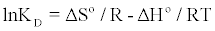 (10)
(10)
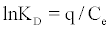 (11)
(11)
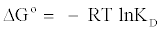 (12)
(12)
The values of ΔH°, ΔS° were calculated from the slope and intercept of Van’t Hoff plot of lnKD versus 1/T (Figure 10), respectively. Positive values of ΔH° indicated the endothermic nature of adsorption (Table 3). And it was further suggested physisorption because the ΔH° value obtained in this study was lower than 40 kJ/mol [21,22]. The positive value of ΔS° means the adsorption system favored increased disorder and randomness at the solid-solution interface. The randomness might be attributed to the displaced water molecules gaining more translational entropy as compared to that lost by the dye molecules during the adsorption [23]. The Gibbs free energy was negative and increases towards the negative side with rise in temperature, indicating the adsorption process to be spontaneous in nature and more favourable at higher temperature. Thus, the reaction was endothermic and spontaneous at all temperatures [24].
| Temperature(K) | KD | Thermodynamic parameters | ||
|---|---|---|---|---|
| ΔH°(kJ/mol) | ΔS°(KJ/mol.K) | ΔG°(kJ/mol) | ||
| 303 | 1.90 | 29.971 | 0.103 | -1.612 |
| 313 | 2.46 | -2.342 | ||
| 323 | 3.65 | -3.464 | ||
| 333 | 5.58 | -4.761 | ||
Table 3: Thermodynamic data for adsorption of MB onto DPF.
The adsorption of MB from aqueous solution using DPF has been investigated, and the following results are obtained:
- DPF was effective, as a MB adsorbent, for which the removal reached 98% MB at 30°C.
- The optimum pH for the uptake was found to lie between (6 and 8).
- Increasing temperature and particle size reduction lead to increasing the removal of MB.
- The Langmuir isotherm model appears to be the best fitting model than Freundlich isotherm model for adsorption of MB by adsorption on DPF.
- The kinetics of MB adsorption on the DPF was found to follow a pseudo second-order rate equation.
- Thermodynamic parameters (ΔG°, ΔH°and ΔS°) showed that the adsorption process is spontaneous and endothermic in nature.