The primary goal of oil field exploration is to identify and quantify hydrocarbon reservoirs and to estimate their producibility. In a typical exploration, a wellbore (about 15 to 30 cms in diameter) is drilled through earth formation to a depth that may extend to a few kilometers. Estimation of earth formation properties (conductivity σ, permittivity o, hydrocarbon saturation, pressure, mobility, etc.) and the placement of the wellbore in a desired earth layer are challenging problems both in terms of designing the associated sensors, and transmitting, processing and interpreting the acquired data. Conductivity measurements help identify the hydrocarbon bearing layer. For logging while drilling applications (Figure 1), an array of sensors is attached to the drilling bit. These sensors are based on galvanic, induction and propagation properties of electromagnetic fields in the formation. The basic topologies and operations of these sensors include multiple transmitters and receivers along the length operating at a set of frequencies. The received signals are then processed to yield formation parameters of interest, e.g., formation resistivities, anisotropy, and bed boundary locations.

Figure 1: A typical logging while drilling setup for oilfield exploration.

Existing EM sensors for formation conductivity measurement typically employ a continuous wave signal of specified frequency in a few KHz to MHz range. Two major problems associated with the existing frequency-domain measurement approach are: (a) the direct coupling between transmitter and receiver; and (b) the long length of the sensor array. In recent years, there has been some interest in exploring Pulsed Electromagnetic (PEM) measurement which has the potential to mitigate the earlier mentioned problems. A few recent papers and patents [1-4] have brought the topic of PEM to the fore.

There are many challenges in the design and operation of PEM sensors for Logging While Drilling (LWD) applications. The purpose of this paper, however, is to address the challenges associated with electromagnetic modelling of such sensors. In this study, we consider both the electric as well as magnetic dipoles embedded in a layered medium. The difficulty encountered when attempting to use the existing FDTD solvers is that they are not efficient for such low frequency problems because of several reasons [5,6]. First of all, the antenna geometry becomes smaller than the wavelength at low frequencies. Consequently, the time-step is very small because of spatially fine mesh needed to adequately represent the transmit and receive antennas. In addition, a low frequency excitation pulse has large time duration. Furthermore, the complexity of the FDTD increases 16-fold when the mesh size is halved, and renders the FDTD computationally very expensive. Therefore, it becomes necessary to run the FDTD simulation for several million time steps to reach a convergent solution. Second, the present state-of-the-art absorbing boundary conditions (ABCs) cannot absorb evanescent waves when the frequency is low; hence the size of the computational domain has to be large to avoid reflection of the evanescent waves from the ABCs, which further increases the memory requirement as well as the computational time. Hence, it is not uncommon to have to wait for a very long time (even a few days) because the problem at hand may require 100s of GB of memory and has to be run for millions of time steps to reach a convergent solution. Obviously, this is undesirable in practical applications since the decision to drill further is based on real-time information about the composition of the layers below. In the context of the MoM, deriving a full-wave solution at low frequencies is problematic as well, because of the low-frequency breakdown problem that arises since the electric field (E) contribution from vector potential term (jωA) becomes several orders of magnitude smaller than the scalar potential term (∇φ) as ω → 0 (See (1)), which, in turn, renders the MoM matrix highly illconditioned [7]. The objective of this paper is to present a technique which circumvents these problems.

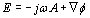(1)

The rest of the paper is organized as follows. In Section II, we describe the geometry of a typical multilayer problem and propose solutions to model the multilayer geometry using the FDTD and MoM. Numerical results calculated by using the FDTD and MoM simulations with the proposed modifications described in Section II are presented in Section III. Section IV describes the methodology used for voltage calculations from the simulation results and, finally we conclude in Section V with key observations and possible future work.

To describe the method, we consider a layered medium of earth formation as shown in Figure 2, where the ith layer has the permittivity ∈_ri ranging from 10-50, conductivity σri ranging from .001-1 S/m, and the thickness Di ranging from 60-610 cm. The distance d between the transmit and receive antennas varies from 30-60 cm. Only a single axial antenna has been shown for the purpose of illustration. But in reality, triaxial transmitters and an array of triaxial receivers may be used. Also, both electric and magnetic dipoles can be used as the source and receive antennas, although it is preferable to use the magnetic dipoles as will be shown later.

Figure 2: Problem geometry.

In LWD the depth of investigation depends upon the frequency of the source. The lower the frequency the smaller the attenuation of the signal will be, resulting in larger depth of investigation. In the PEM approach, we make use of cross, coplanar and coaxial time domain voltage measurements from an array of receive antennas when an antenna transmits a low frequency pulse. The received time domain voltage signals are then processed to determine the thickness of the layers and their other properties such as conductivity, dielectric constant, azimuthal and elevation angles of the layers with respect to the sensor axis, etc.

To compute the electromagnetic fields, we employ both the FDTD and the MoM formulations. For PEM applications, FDTD is more attractive since one can directly obtain the voltage as a function of time whereas frequency domain methods such as MoM requires an interpolation in conjunction with an inverse Discrete Fourier transform (i-DFT). It is worth mentioning here that one of the key requirements, apart from the accuracy, is that such a method must be numerically efficient since it may be used as a forward model in an inverse problem formulation; thus it may require numerous executions to determine the properties of the formation.

To facilitate the solution of the low-frequency problem by using the FDTD, we begin with the conventional FDTD algorithm which which uses the differential version of the Maxwell equations given in (2). However, we consider transmit and receive dipoles to be infinitesimally small. This can be done by modifying the FDTD update equations, in which we update the values of the electric or the magnetic fields either at the edge of the source cell or at the center of the source cell, respectively, depending on whether it is an electric or magnetic dipole source, and we do this by using one of the hard-source conditions given in (3). Therefore, we do not need to use a very fine mesh or run the simulation for millions of time steps when we use this approach. The mesh size will be limited by the distance between transmit and receive antennas, which is equal to a few meters in a typical drilling tool.

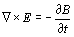
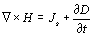(2)

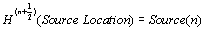(3)

To solve the low-frequency problem in the context of MoM, we consider the source to be a point dipole. Then, we do not need to form the matrix, but can obtain the values of the fields due to a delta source directly from the Green’s function instead.

To illustrate our approach, we consider two different operating conditions, as shown in Figure 3. They include an oil- sand mixture and water-sand mixtures trapped between two layers of shale. The transmitter dipole is excited by using a Gaussian pulse with a 3 dB cutoff frequency of 1 MHz. The mesh size is 20 cm that is λ/1500th of the wavelength at 1 MHz. The computational domain which is a cube of side 11 m, is truncated by using the CPML (Convolutional Perfectly Matched Layer) absorbing boundaries. Both the transmit and receive antenna are represented as dipole of 20 cm so that they match with the mesh size. We first compute the incident field at the receiver by setting the properties of the three layers to be the same, (thus letting the formation be homogeneous) and by exciting the transmitter with a 1 MHz (3 dB cutoff) Gaussian pulse. The same computation is repeated with the inhomogeneous layered formation to derive the total field at the receiver. The difference between the two results, thus obtained, contains information about the layers, and will refer to this difference as the reflected field. For the two scenarios in Figure 3, the time signatures of the total field and the reflected field are evaluated by using the proposed approach for electric and magnetic dipole sources polarized along the x-, y- and z directions.

Figure 3: Oil-Sand/Water-Sand trapped in-between shale.

We begin by considering the case when the transmit antenna is an x-polarized magnetic dipole. As shown in Figure 4, the total magnetic field at the receiver appears to be similar for both the scenarios, namely oil-sand trapped in-between shale and water-sand trapped in-between shale. Therefore, in order to separate the two signals, which reach the receiver directly from the transmitter as well as after reflections at the layer interfaces, we subtract the time signature of the magnetic field at the observation point when the source and receiver are placed in a homogenous medium (shale only), which corresponds to the incident field (Figure 5). This is similar to the hardware coil array design where a bucking coil is appropriately placed along with the main coil to cancel the direct coupling. This procedure yields the signature of the reflected field as a function of time, which is shown in Figure 6. The reflected magnetic field time signature shows a significant difference in amplitude and shape for problems in which either Oil-Sand or Water-Sand occupies the central layer, even though this was not clearly discernible from the total field. The reflected field is higher for oil-sand than it is for water-sand. This is because of the lower conductivity of oilsand mixture compared to the shale. Similarly, the time signatures of the reflected fields for the y and z-polarized transmit magnetic dipoles are shown in Figures 7-10 show the amplitude and phase variations, respectively, of the reflected fields as a function of frequency for an x-polarized magnetic dipole.

Figure 4: Total Hx Field (layered medium) at the receive antenna due to an x-polarized transmit magnetic dipole.

Figure 5: Incident Hx Field (shale only) at the receive antenna due to an x-polarized transmit magnetic dipole.

Figure 6: Reflected Hx field at the receive antenna due to an x-polarized transmit magnetic dipole.

Figure 7: Reflected Hy field at the receive antenna due to a y-polarized transmit magnetic dipole.

Figure 8: Reflected Hz field at the receive antenna due to a z-polarized transmit magnetic dipole.

Figure 9: Amplitude of reflected H x field at the receive antenna due to an x-polarized transmit magnetic dipole as a function of frequency.

Figure 10: Phase of reflected Hx field at the receive antenna due to an x- polarized transmit magnetic dipole as a function of frequency.

Next, we change the transmit antenna to an electric dipole oriented along the x-direction, and calculate the incident (Figure 11), total (Figure 12) and reflected fields (Figure 13). The total fields for the two cases are again found to be nearly the same. The reflected field computed by taking a difference between the total and the incident field is found to be slightly higher for the trapped oil-sand, when compared to the case of trapped water-sand, as may be seen from Figure 13. However, the difference is much smaller for the electric dipole case than when the transmit antenna is a magnetic dipole, and we measure the magnetic fields. Similar behavior was observed for the y- and z-oriented electric dipoles, as shown in Figures 14 and 15. This leads us to conclude that for the current low frequency problems for which the size of the antenna is much smaller than the wavelength, it is better to use a magnetic dipole (coil, for instance) antenna. The amplitude and phase of the reflected electric field as functions of frequency are shown in Figures 16 and 17 for an x-polarized dipole. The present modeling problem was also solved by using the MoM, in which the transmitting antenna was modeled as a point dipole source. The amplitude ratio of the vector to scalar potential is plotted in Figure 18, as a function of the distance of the receiver from the source (y-oriented dipole) by using a layered medium Green’s function formulation [8], for two different scenarios, depicted in Figure 3, at an operating frequency of 1 MHz. From Figure 18 we can clearly see that the low frequency breakdown problem is certain to occur for this problem at 1 MHz, since the scalar potential is nearly eleven orders of magnitude greater than the vector potential which would result in an ill-conditioned MoM matrix. However, we circumvent this problem and are able to extract accurate solutions because we are using a point dipole source and, hence, we can compute the field values analytically by using the Green’s functions directly, without having to employ a matrix formulation in the context of MoM to compute these values.

Figure 11: Incident Ex Field (shale only) at the receive antenna due to an x-polarized transmit electric dipole.

Figure 12: Total Ex Field (layered medium) at the receive antenna due to an x-polarized transmit electric dipole.

Figure 13: Reflected Ex Field (layered medium) at the receive antenna due to an x-polarized transmit electric dipole.

Figure 14: Reflected Ey Field (layered medium) at the receive antenna due to a y-polarized transmit electric dipole.

Figure 15: Reflected Ez Field (layered medium) at the receive antenna due to a z-polarized transmit electric dipole

Figure 16: Amplitude of reflected Ex field at the receive antenna due to an x-polarized transmit electric dipole as a function of frequency.

Figure 17: Phase of reflected Ex field at the receive antenna due to an x- polarized transmit electric dipole as a function of frequency.

Figure 18: Amplitude ratio of the vector to scalar potential for a y-polarized transmit electric dipole as a function of distance between the transmitter and receiver.

Ultimately, the voltage and the current values are the ones that are measured in practice, rather than the fields. The voltage induced in the receive antenna (coil) due to the reflected fields from the interface of the layered media can be calculated by using the Faraday’s law, from which we know that when a loop with area A and N turns is placed in a timevarying magnetic field (B), an EMF is induced in the loop, and is given by:

(4)

where μ is the permeability of the medium and H is the magnetic field strength at the location of the coil in A/m. For our case, H is on the order of 10-4 A/m. Assuming coil radius of 5 cms with air core (μr=1) and 100 turns, voltage induced will range from 62 μV to 62 mV over a frequency range of 1 KHz to 1 MHz.

In this work we have investigated the fields generated by electric and magnetic dipoles embedded in a three layered earth formation, using the FDTD and the MoM formulations. We have found that, it is preferable to use a magnetic dipole instead of an electric dipole, since the reflections from the interface depend on the relative permittivities and conductivities of the layers. The case of oil-sand mixture trapped in between shale shows a higher level of reflected magnetic field, as compared to the case of water-sand mixture also trapped in-between shale. This is because of the lower conductivity of oil-sand when compared to shale. The scalar potential term was found to be much larger than the vector potential term, indicating the low-frequency breakdown is almost certain to occur, even at the highest frequency of interest (1 MHz) if we try to form the MoM matrix. But this issue of breakdown has been circumvented by evaluating the fields for a pointtype electric or magnetic dipole source analytically, by using the Green’s function. In future, we propose to evaluate the fields analytically by using the scalar and vector potential information to validate the FDTD results, since we plan to model three orthogonal magnetic dipoles, oriented at an angle with the layered medium. Our objective would be to evaluate the apparent dip angle (ν) [9,10], distance D and conductivities of the layers by doing cross, coaxial and coplanar measurements, using a step excitation as the set of transmitting magnetic dipoles