Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Research Article - (2015) Volume 2, Issue 4
In this paper, a computational study of medium effect on solvation free energy, dipole moment and different molecular properties like global reactivity descriptors (chemical hardness, softness, chemical potential, electronegativity, electrophilicity index) of naproxen have been reported. Hartee–Fock (HF) and Becke, 3-parameter, Lee-Yang-Parr (B3LYP) level of theory with 6-31G(d) and 6-31G(d,p) basis sets were applied for gas phase and solution. The solvation free energy, dipole moment and molecular properties were calculated by employing two solvation models namely polarizable continuum model (PCM) and Solvation Model on Density (SMD). For all levels of theory, the solvation free energies were gradually increased in going from lower to higher dielectric constant for PCM, but opposite result was observed in case of SMD model. However, with SMD, the solvation free energies were higher than that of PCM in all the solvent systems. The dipole moment of naproxen was found to be increased when going from non-polar to polar solvents for both PCM and SMD model. The dipole moment of naproxen was higher in different solvents than that of the gas phase. Moreover, Ongoing from non-polar to polar solvent the chemical potential, electronegativity and electrophilicity index were increased regardless of the solvation models, basis sets and level of theories used. On the other hand, no noticeable medium effect was observed on chemical hardness and softness. The results obtained in this study may lead to understand the stability and reactivity of naproxen and the results will be of assistance to use the title molecule in reaction intermediates and pharmaceuticals.
<Keywords: Naproxen; Solvation free energy; Dipole moment; Solvation model
Non-steroidal anti-inflammatory drugs (NSAIDs) are an important class of compounds that display a number of effects as a consequence of their ability to block cyclooxygenase (COX) involved in the first step of the arachidonic acid cascade [1]. COX exists in two isoforms named COX-1 and COX-2. The first is constitutively expressed in the stomach, the kidneys, and platelets and is considered important in mucosal protection and platelet function. COX-2 is inducible and plays a major role in prostaglandin biosynthesis in inflammatory cells [2]. Naproxen (Figure 1) is a non-steroidal anti-inflammatory drug (NSAIDs) with analgesic, antipyretic and anti-inflammatory properties. It is a nonselective COX-2 inhibitor and inhibits both the isoforms of COX enzyme. The desired analgesic, antipyretic and anti-inflammatory activities of naproxen are obtained as a consequence of the inhibition of COX-2; on the other hand, inhibition of COX-1 leads to unwanted effects on the gastrointestinal tract such as ulceration, bleeding and perforation of gastrointestinal tract [1]. To reduce this unwanted effects attempts were made to synthesize less toxic naproxen derivatives [3]. A few computational and theoretical studies on naproxen were reported earlier. Jubert et al. investigated the vibrational and theoretical studies of naproxen [4]. Okulik and Jubert reported the theoretical study on the structure and reactive sites of naproxen (Figure 2) [5]. Moreover, Musa and Eriksson investigated the theoretical study of naproxen photo toxicity [6]. As a part of our ongoing research [7,8] the present study was undertaken and to the best of our knowledge, the medium effect on the solvation free energy, dipole moment and global and local reactivity descriptors (chemical hardness, softness, chemical potential, electronegativity and electrophilicity index) have not been previously reported.
Computational methods
All calculations were performed in Gaussian09 software package [9]. The geometries of the titled compound were optimized before performing any calculation. The absence of imaginary frequencies in the optimized structure confirmed that the stationary points correspond to minima on the potential energy surface. The solvation free energies, dipole moment and molecular properties were calculated on HF and B3LYP level with 6-31G(d) and 6-31G(d,p) basis sets. The Polarizable Continuum Model (PCM) and Solvation Model on Density (SMD) were used for all types of calculation.
Solvation free energy and dipole moment
The most important properties of a solute surrounded by solvent can best be described by the free energy change [10]. In this study, we compared the PCM and SMD models. However, the SMD model is recommended for calculating solvation free energy in Gaussian09. The calculated solvation free energies of naproxen are presented in Table 1. For all levels of theory, the solvation free energies were gradually increased in going from lower to higher dielectric constant for PCM, but opposite result was observed in case of SMD model. In the two models, a significant change was observed in going from a non-polar to a polar solvent. Basis sets had no remarkable effect on the solvation energy for both models. In addition, solvation free energies at HF level of theory were more negative than that of B3LYP with PCM and SMD. For all solvents, SMD gave relatively higher solvation energies than that of PCM. The solvation free energy change from water to n-octanol (ΔGtro→w) was positive in case of PCM leading to the conclusion that diffusion of naproxen from water to n-octanol is not spontaneous process, but SMD gave quite opposite result which is in a good agreement with the experimental logP (3.18) value of naproxen. The positive ΔGtro→w value obtained from SMD model revealed that naproxen is a lipophilic molecule and will cross the lipid bilayer membrane easily. Hence, a prediction can be made regarding the lipophilicity or hydrophilicity of molecule from the ΔGtro→w value.
| Medium(dielectric constant) | PCM | SMD | ||||||
|---|---|---|---|---|---|---|---|---|
| 6-31G(d) | 6-31G(d,p) | 6-31G(d) | 6-31G(d,p) | |||||
| HF | B3LYP | HF | B3LYP | HF | B3LYP | HF | B3LYP | |
| H2O (78.3) | -9.1 | -7.1 | -9.5 | -7.2 | -11.5 | -7.9 | -12.8 | -7.5 |
| n-Octanol (9.9) | -7.6 | -6.1 | -7.9 | -6.2 | -12.8 | -10.1 | -13.1 | -10.2 |
| ΔGtro→w | 1.5 | 0.9 | 1.6 | 1.0 | -1.3 | -2.2 | -0.3 | -2.6 |
Table 1: Solvation free energy (Kcal/mol) of Naproxen in different solvents with PCM, CPCM and SMD.
The dipole moment is expected to be larger in solution than in the gas phase. Table 2 presents the dipole moments computed in the gas phase and in two solvents (H2O and n-octanol) at the different level of theories (HF and B3LYP) with 6-31G(d) and 6-31G(d,p) as basis sets using PCM and SMD solvation models. All the dipole moments calculated with B3LYP level were larger than that calculated with HF. The difference between the dipole moments in different solvents calculated at B3LYP and HF with 6-31G(d) and 6-31G(d,p) basis sets varied from 0.20 to 0.28 and 0.20 to 0.39 Debye, respectively. Generally, from lower to higher dielectric constant, the dipole moment increased steadily regardless of the theory.
| Solvation Model |
Medium(dielectric constant) | 6-31G(d) | 6-31G(d,p) | ||
| HF | B3LYP | HF | B3LYP | ||
| Gas | 1.23 | 1.30 | 1.23 | 1.30 | |
| PCM | H2O (78.3) | 1.47 | 1.68 | 1.49 | 1.70 |
| n-Octanol (9.9) | 1.43 | 1.63 | 1.45 | 1.65 | |
| SMD | H2O (78.3) | 1.45 | 1.73 | 1.47 | 1.88 |
| n-Octanol (9.9) | 1.44 | 1.75 | 1.46 | 1.76 | |
Table 2: Dipole moment (Debye) of Naproxen in gas phase and in different solvents using PCM and SMD.
Global reactivity descriptors
The energy gap between HOMO and LUMO is a critical parameter to determine molecular electrical transport properties. By using HOMO and LUMO energy values for a molecule, the global chemical reactivity descriptors of molecules such as hardness, chemical potential, softness, electronegativity and electrophilicity index have been defined [11-15]. Pauling introduced the concept of electronegativity as the power of an atom in a molecule to attract electrons to it. Using Koopman’s theorem for closed-shell molecules the hardness (η), chemical potential (μ) and electronegativity (χ) and softness (S) are defined as follows.
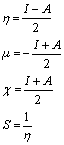
Where I and A are the ionization potential and electron affinity of the molecules, respectively. The ionization energy and electron affinity can be expressed through HOMO and LUMO orbital energies as I=- EHOMO and A=-ELUMO.
Considering the chemical hardness, large HOMO–LUMO gap means a hard molecule and small HOMO–LUMO gap means a soft molecule (Table 2). One can also relate the stability of the molecule to hardness and softness. Molecule with least HOMO–LUMO gap is more reactive and vice versa. Parr et al. have defined a new descriptor to quantify the global electrophilic power of a molecule as electrophilicity index (ω), which defines a quantitative classification of the global electrophilic nature of a molecule (Table 3) [14]. Parr et al. have defined electrophilicity index (ω) as follows [14]:
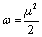
Using the above equations, the chemical potential, hardness and electrophilicity index were calculated. These reactivity quantities are very useful in understanding the toxicity of compounds in terms of their reactivity and site selectivity [16-18]. The molecular properties of naproxen in gas phase and in different medium are presented in Table 4. Ongoing from non-polar to polar solvent the chemical potential, electronegativity and electrophilicity index were increased regardless of the solvation models, basis sets and level of theories used. On the other hand, solvent systems had no noticeable effect on chemical hardness and softness.
In the present work, the medium effect on solvation free energies, dipole moment and global reactivity descriptors have been determined from HF and DFT calculations using 6-31G(d) and 6-31G(d,p) as basis sets. From the calculated value of ΔGtro→w a prediction regarding the lipophilicity of a molecule can be made provided that the SMD model is used. The HOMO–LUMO energy gap has been calculated to get the global reactivity descriptors of the titled molecule. The calculated molecular properties may lead to understand the stability and reactivity of naproxen and the results will be of assistance to use the title molecule in reaction intermediates and pharmaceuticals.