Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2013) Volume 6, Issue 8
The three-dimensional structure of a protein molecule provides significant insight into its biological function. Structural alignment of proteins is an important and widely performed task in the analysis of protein structures, whereby functionally and evolutionarily important segments are identified. However, structural alignment is a computationally difficult problem and a large number of heuristics introduced to solve it do not agree on their results. Consequently, there is no widely accepted solution to the structure alignment problem. In this study, we present a meta-analysis approach to generate a re- optimized, best-of-all result using the alignments generated from several popular methods. Evaluations of the methods on a large set of benchmark pairwise alignments indicate that TMalign (Template Modeling Alignment) provides superior alignments (except for RMSD, root mean square deviation), compared to other methods we have surveyed. Smolign (Spatial Motifs Based Multiple Protein Structure Alignment) provides smaller cores than other methods with best RMSD values. The re-optimization of the alignments using TM-align’s optimization method does not alter the relative performance of the methods. Additionally, visualization approaches to delineate the relationships of the alignment methods have been performed and their results provided
Keywords: Meta-analysis; Protein alignment; Structure comparison; Benchmark test; Meta-program
Fold comparison software is important by itself for a number of reasons, not the least of which is the determination of function. For example, the function of a newly discovered protein can be determined by comparing its structure to some known ones. If a protein’s folds have already been determined and its function is known, then a new protein with similar folds should have similar function. Additionally, making new protein families may be possible with fold comparison software. Given a particular set of proteins and their structures, one can cluster them in families based on their structural similarities. Of course such a classification may take some time to determine accurately for all potential families, but is possible in theory, by defining a consensus structure for each family, solving an MSTA (multiple structural alignment) problem.
Structure alignment is a computationally difficult problem and the proposed methods rely on heuristics. TM-align uses a unique method for weighting its distance matrix, to which dynamic programming is then applied; a benchmarking study puts it ahead of CE (Combinatorial Extension) in speed and accuracy [1]. CE breaks the proteins into comparable fragments. However, CE creates what are called AFPs (aligned fragment pairs) that are used to define a certain similarity matrix through which only the optimal path is generated to create the final alignment using greedy search algorithm methods [2]. FATCAT (Flexible structure AlignmenT by Chaining AFPs with Twists) is a rather new algorithm, and it uses AFPs with twists, like the name implies. This incorporates conformational flexibility into the alignment by combining gaps and twists between consecutive AFPs, each with its own score penalty [3]. Smolign is an MSTA tool that is centered around mRMSD (multiple RMSD), a special RMSD calculation for MSTAs. It uses a distance matrix as well, and looks into secondary structural elements or SSEs, which is not uncommon in the realm of protein alignment algorithms. It can be rigid or flexible, is enhanced by an Enhanced Partial Order curve comparison algorithm, and it is centered around small cores and how they align, giving multiple potential alignment results, of which the best result was used [4].
The five programs were chosen based on a Google search for citation popularity of the original articles. TM-align and CE were by far the most cited (by 375 and 1540, respectively), and FATCAT was well cited too (by 200) for a newer program. Smolign was only cited by 1 but it was included because it was an MSTA program we knew intimately and there was full access to the code.
This study presents a novel approach to compare and visualize the results of multiple alignment methods.
A wrapper function was generated in MATLAB to run TM-align [1], CE [2], jCE (java CE) [3], jFATCAT (java FATCAT) [3,5], and Smolign [4] simultaneously and compare results. A website will be created in the near future with additional programs for meta-analysis.
The 1704 pairs from Kolodny et al. [6] were made in an attempt to insure sequence diversity. It is a test set of domains intended to lead to a more accurate evaluation of the numerical and graphical results involved. Kolodny et al. [6] considered CATH format, not SCOP to be the “gold standard” for classifying domains. CATH is an acronym that details the levels of its hierarchy of protein classification - Class, Architecture, Topology, and Homologous superfamily - and SCOP simply stands for Structural Classification of Proteins, and this gives one an idea of the difference between the two styles of classification. And since Kolodny et al. [6] makes a strong case for CATH, this study thus utilizes the CATH format for protein domains. The study by Kolodny et al. [6] intended to delineate the reasons as to why there should be a “best-of-all” method that provides the best results of all methods, in part, inspiring this study. The list was used to obtain all results, but the meta-program can still run proteins and domains outside of the list without problems, including obsolete domains, if they still exist somewhere in the CATH database, a database for protein domains and fragments, similar to SCOP, another such database.
As an evaluation metric, TM-score, RMSD, SAS score, portion of coverage and the time it took each algorithm to run was used. PCA (principal component analysis) and hierarchical clustering was performed on a few of the resultant metrics, namely, RMSD, Min-TMscore. Rotation and translation matrices were also used as an input for PCA and clustering.
The total number of functions being five, and having more than sufficient data, this study covers a range of the top-rated (by number of articles citing the function’s original paper) structural alignment functions.
The methods varied in their output. Whenever a structure alignment was not provided, we used Kabsch’s method to obtain rotation/translation matrices. Whenever residue correspondences were not provided, we used the TM-score method to collect residue pairs from the structure superposition.
For a better interpretation of the results the scores are explained here. The runtimes given above are simply a direct average calculation of how long it took for just the alignment method itself to run for the pairs involved in each case. The RMSD calculation used is cRMS, which is
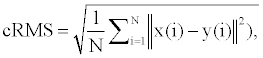 (1)
(1)
where the N is the length of atoms in the aligned pieces of protein, and x(i) and y(i) represent each proteins coordinates in each atom of the proteins as the norm of those three-dimensional coordinates is calculated [7]. SAS score is
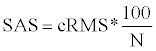 (2)
(2)
where N is the number of matched residues [8]. TM-score is, after optimal spatial superposition, the maximum value of
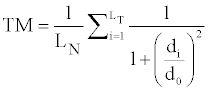 (3)
(3)
where LN is the length (number of residues) of the native structure, LT is the number of the residues aligned to the template structure, di is the distance between the ith pair of aligned residues and d0 is a scale for normalizing the match difference [9]. Min-TM-score is defined by taking the smaller protein as LT. The reason TM-optimization was used was because it was hypothesized, based on knowledge of Kabsch’s algorithm and how TM-align utilizes it, that it would make the rotation and translation matrices converge for all the methods and raise the TM-score for all results.
The results substantiate the suggestion that the newer structural alignment programs are better than the older ones. The average length of alignment was a choice that would vary too greatly statistically depending on the protein sizes involved in the alignments, so N-align ratio (ratio of residues aligned) was used in its place which is the percentage of aligned protein lengths in relation to total lengths. It is not the same as percentage identity, which is calculated differently in each algorithm [10]. According to Table 1 on the right, TM- align is the best-scored protein structure alignment tool except for RMSD and its extremely low number of failures is inconsequential.
| Method | TM-align | Smolign | jFATCAT | jCE | CE |
|---|---|---|---|---|---|
| Time (seconds) | 0.489632 | 16.65826 | 4.2375 | 4.006021 | 20.43188 |
| N-align ratio | 0.485208 | 0.251817 | 0.416713 | 0.406333 | 0.40698 |
| SAS Score | 5.842223 | 7.671572 | 8.309964 | 8.60021 | 8.611393 |
| RMSD (cRMS) | 4.987481 | 2.919341 | 5.696137 | 5.869022 | 5.888683 |
| Min-TM-score | 0.361763 | 0.23495 | 0.245424 | 0.234077 | 0.234188 |
Table 1: Average statistics for 1704 protein pairings.
SAS score is an interesting indicator of an effective alignment, and it should be as low as possible. Both a low cRMS is preferred along with a large length of alignment in general, particularly for an ideal SAS score, and it shows that there is very little variation for a large alignment which is better than a program like Smolign that has the lowest N-align ratio, but the lowest cRMS of all functions by far. Smolign actually has the second best SAS score, but compared to TM-align’s, which is vastly better for a much larger average alignment and only slightly higher cRMS, it is likely not the superior program. Smolign performs well, considering it is MSTA software based on using small sectional cores in each protein, which explains its second slowest runtime next to CE. Table 1 point out CE as the worst of all the methods based on the heuristic benchmark test. TM-align had an expectedly higher TM-score, around 0.1 or more on the average, which is actually rather significant. Based on the table above, jCE and its counterpart CE are statistically in competition for the worst function of the five based on the benchmark. If not for the extremely low RMSD that Smolign achieves, the fact that it by far possesses the lowest N-align ratio is a negative facet that does not act in its favor. Since Smolign is centered around RMSD, having the best RMSD value is not surprising. However, Smolign was not made for protein pair alignments exclusively as the other functions were which definitely plays a role in its poorer results in tests aimed toward such functions. Despite that, it’s TM-score, when compared to jCE and CE and even jFATCAT is nearly equal. And furthermore, RMSD is still considered a strong, lasting measure of protein similarity in structure alignment tools, which is to Smolign’s benefit.
CE did well in comparison to its newer counterpart, jCE.
Other than speed, in all other areas they were approximately the same. jFATCAT did far better than jCE though, and overall it was the second best function of all the functions in terms of the established metric. Its algorithm is newer and more versatile, like TM-align and unlike CE, which may have contributed to its superior results. From left to right, Table 1 is in order from best method to worst method based on the results of that table, using a significant difference in TM-score as a factor, and a significant difference in RMSD and SAS to make it fair for all programs since TM-align achieved a higher TM-score than the rest, while the others had nearly equal TM-scores and varied RMSD values. To remove a potential bias towards TM-align, as also seen in Table 1 above, the results for all methods were TM-optimized, or rather had their pairings and rotational/translational matrices aimed towards achieving a high TM-score, for all functions in the metaanalysis software. The TM-optimization algorithm in the meta-analysis software takes the pairs and changes the rotation, translation matrices and TM-score using the TM-align algorithm which keeps track of the best TM-score, the best rotation matrix, and the best translation matrix, and updates the pairs, rotation and translation matrices and TM-score based on the stored best values for the results of any method, even TM-align itself. These results are in Table 2 below.
| Method | TM-align | Smolign | jFATCAT | jCE | CE |
|---|---|---|---|---|---|
| N-align ratio | 0.498518 | 0.395962 | 0.431436 | 0.435041 | 0.43509 |
| SAS Score | 5.944499 | 7.233359 | 7.359396 | 7.319987 | 7.319018 |
| RMSD (cRMS) | 5.340631 | 5.286898 | 5.711302 | 5.756867 | 5.756953 |
| Min-TM-score | 0.358948 | 0.294548 | 0.297715 | 0.296126 | 0.296153 |
Table 2: TM-Optimized Results Table.
Three facets of this table stand out instantly. One is the marked increase in all functions’ Min-TM-scores (with the exception of TMalign). Another is a large increase in Smolign’s RMSD score. The third is the significant increase in the methods’ N-align ratio in the optimization. Since SAS is dependent on both RMSD and N-align ratio, it is a fair indicator of which alignment methods have the best RMSD for the largest alignment. By that logic, Smolign is the second best method next to TM-align for both tables of results, as using only TMscore would be biased, and while Smolign’s RMSD went up significantly with optimization, the N-align ratio also went up. This merely supports the notion that Smolign uses small cores for comparison while keeping the lowest possible RMSD score for the largest possible alignment, but focusing more on the RMSD. Smolign, comparatively speaking, had an extremely low RMSD score and the second lowest SAS score in Table 1, and maintains the second lowest SAS score in Table 2 as well, despite the RMSD score increase. TM-align is better than the other methods overall in both tables except for RMSD, and in Table 2, the difference is not large for RMSD. Unsurprisingly, the TM-score value for the four other programs after optimization is much closer comparatively to TM-align’s TM-score.
In Figure 1, for the protein domain pairing 1a12C00 and 1b4vA01, the different superpositions of the proteins are shown as they are displayed in Jmol. The different manner, in which each function aligns its protein pair, as well as how those manners are ever similar, can be seen in these figures. The darker, thicker lines indicate which parts of the proteins are being aligned. The first protein, PDB ID 1a12, Chain C, domain 0, is the yellow colored one, being larger, and the second, 1b4v, Chain A, domain 1, is the purple colored one, as it is smaller. In the Jmol viewer, one can view atomic coordinates and what residue the cursor is over.
In Figure 1 above jCE and CE produce an identical alignment as foreshadowed by the numerical results. Smolign looks entirely different from the other four. Its core-based alignment methodology and the motif library it generates when running, contribute to the unique way it aligns two structures versus the other four methods. jFATCAT’s superposition contains a significant amount of alpha-rich regions in its alignment as well, another noteworthy facet of its alignment which incorporates twists. TM-align aligns a much larger section (as evidenced by its consistently largest N-align ratio) of the two proteins, and the two proteins overlay more smoothly than the other three pair-based methods, but Smolign’s alignment has an even more smooth, precise overlapping to it. Smolign’s structures are the most closely overlapped of the five pictures in Figure 1, as it takes two proteins and finds one section that is extremely similar between the two proteins based on RMSD. That particular alignment then has little variation between the two involved protein domains, particularly when the RMSD value is as small as it was in Table 1. In Figure 2, one can see the differences in the same pair alignment with TM-optimization. From Figure 2, TM-align’s alignment after optimization is not much different from its alignment in Figure 1. The other four methods’ alignments have expanded their size somewhat but Smolign’s grew much larger and now covers a much less closely superimposed section of the two proteins. As evidenced by its changed RMSD score, the nature of Smolign’s alignment after TMoptimization has changed completely. Other than Smolign, however, the other four methods still align what are generally the same regions.
Kabsch’s algorithm, used to calculate rotational and translational matrices while still minimizing RMSD, is generally considered equivalent to the quaternion method used by Smolign. To see if perhaps all protein alignment software uses an equivalent method for generating these matrices, or at least TM-align, clustering was performed on these matrices with and without TM-optimization [11]. The clustergram function used in MATLAB standardized the values in each case along the rows of data, then clustered along the columns of data and next along the rows of data. It uses Euclidean distances to calculate the pairwise distances between rows and columns of data. The rows and row clusters in this case are irrelevant, but give one an idea of how the groups are formed. By default it uses the linkage function implementing the shortest distance method to create the clusters. It is centered around an average, and utilizes the red-green color map, in which red represents values above the mean, black represents the mean, and green represents values below the mean of a row (value) across all columns (samples). The column clusters show just how closely related the methods are by their rotation and translation matrices, RMSD scores, and by their TM-scores and Min-TM-scores. The clustering was done before and after optimization.
The clustering results in Figure 3 show the relationship between methods and elucidate their similar algorithmic methodologies using the RMSD value as a point of distinction. Unexpectedly, after TMoptimization there is not much difference in the relationship between the five methods in terms of rotation and translation matrices (figure not shown). All of the clustering graphs further the case that jCE and CE are the same, but do show very slight variations in their relationship from non- to TM-optimized, particularly clustered by RMSD score in Figure 3.
TM-align is very similar to jCE and CE in terms of RMSD clustering before TM-optimization, but afterwards it displays a strong similarity to jFATCAT and even Smolign, which before optimization is very distant from the other methods in terms of RMSD clustering due to the nature of its algorithm, shown in Figure 3.
For TM-score clustering before and after optimization, TM-align has an expected mean value superiority in comparison to the other methods (figure not shown). Smolign shifts from the far left to the right away from jCE/CE after optimizing. jFATCAT also makes a shift to the right side towards Smolign and TM-align after optimizing, an interesting result that is perhaps indicative of the flexible nature of jFATCAT’s structural alignment algorithm.
Figure 4 below contains the PCA results for RMSD, and the purpose is of a similar nature to that of the clustering: implying that if for one method a particular score did not come out as planned, a method far-removed according to the PCA charts presents itself as an apt consequential decision. This provides the user of the meta-program the option of alternatives to any one method for any protein pairing, as is the purpose of a catch-all meta-program like the one created for this analysis.
PCA analysis of the rotational/translation matrices yields only slightly different results before and after TM-optimization (figure not shown). It shows, as before, that jCE and CE are the same. It shows that in terms of rotational and translation matrices, TM-align and jFATCAT are very similar, indicating a potential similarity in the generation of those matrices, owing to a algorithmic similarity.
In Figure 4, the RMSD-based PCA analysis demonstrates what is a rare difference between jCE and CE. This likely lends itself to a slight computational difference in the implementation of these methods. jFATCAT is by itself as is Smolign, as their methods are very different from the other three conceptually, and RMSD is perhaps the most varied score across different alignment methods. TM-align is surprisingly similar to CE and jCE in this case, implying that CE and jCE’s fragmented method of computation may be spacially similar to TM-align’s unique matrix methodology.
After TM-optimization, Smolign and TM-align become very similar in terms of RMSD and the results in Tables 1 and 2 show this as well.
As with the clustering before, Min-TM-score’s and TM-score’s PCA results are nearly identical. Smolign is shown to be similar to jCE and CE in terms of TM-score, and likewise jCE to jFATCAT but not Smolign to jFATCAT. TM-align is far removed from the other four methods, as expected. This relationship does not change after TMoptimization (figure not shown). If trying to improve one’s score in a particular category, it may be prudent to use another method far-removed from the one previously used, such as indicated by the PCA analysis diagrams. Smolign is an extremely different, effective alternative to most of these methods, and TM-align also distinguish itself in the PCA analysis and clustering. jFATCAT has unique qualities about it that make it different from jCE and CE as well - one of the methods is always similar to the two in each case. Choosing of a different method should be done on a case-by-case basis or in a project centered around a particular score.
To properly illustrate the novelty of this approach, it should be noted that before there was no established approach for the metaanalysis of these proteins. This study proposes a way to compare the five given methods in a meta-analysis system. It speaks persuasively in favour of such a tool in the comprehensive literature review given in the introduction. It clearly delineates the choices made via a proof-ofconcept system using the number of citations per article and software availability, and of the data sets selected for the evaluation of the systems. The conclusion is that recent software has brought forth improvements, both in speed and in accuracy. The meta-analysis program allows one to choose from five different methods, two of which are slight variations of the same method. It allows for the incorporation of future programs more easily by way of its standardized input and output - thus compiling and making an individual program run successfully becomes the only real difficulty, and parsing the data in a useful manner requires no extra thought. The results of the meta-analysis showed that of the five, TM-align was the best method based on the provided metric, with Smolign as second best. The initial hypothesis that TM-optimization is able to converge different alignments in terms of rotation and translation matrices, was proven incorrect, however there were striking similarities observed in RMSD clustering after TMoptimization, and all n-align ratios were increased significantly as well, reducing SAS score despite an RMSD increase.